风场环境的建模与预测, 需要对大量历史数据进行处理和分析, 有效提高建模与预测效率和精度值得深入研究[4]。本征正交分解(Proper Orthogonal Decomposition, POD)是风场建模中常用的一种方法, 将风场数据通过特征值分解为本征模态和主坐标的组合, 其中本征模态主要与空间因素相关, 主坐标主要与时间因素相关, 物理意义明确, 通过模态截断还能提高计算的效率[5]。
目前, POD方法已被广泛地应用于解决实际问题数值模拟的降维问题中。Holmes等[6]采用气动平均的方法对双坡屋盖的表面压力进行测量, 指出POD方法是描述钝体风压的有效途径。Fic等[7]将POD方法的离散形式应用于线性和非线性瞬态热传导的降阶模型中。Tan等[8]应用POD结合三次样条插值方法对流场压力系数进行预测。对于风场建模, 胡亮[9]利用POD方法对具有桥塔风效应的风场进行了简化模拟, 将POD型谱表示法取代原型谱表示法, 物理意义明确且可通过模态截断节省计算量。陶青秋[10]将POD方法用于分析在大跨屋面和高层建筑物上的风致响应, 利用POD与结构模态相结合的双模态方法来分析结构的动态响应, 表明POD方法是一种有效分析多激励响应的方法。邹垚等[11]通过对POD原理进行修正后用于风洞实验风场的重建, 主要通过修正第一个本征模态值, 对偏差较大测点的风压场重建进行改进, 使重建风场的方差值与实际风场方差值的差距大大缩小。Chen和Kareem[12]利用POD方法对建筑结构的数值风场进行了模拟并提出了状态空间建模方案, 建立了风载荷与建筑结构共振响应在物理意义上的联系, 有助于更好地了解结构随时空变化的动态负载响应。
本文基于适用于平流层风场环境的POD方法, 以长沙地区风场数据为例, 研究平流层风场随高度和时间的变化特点, 通过POD方法对风场数据进行降阶处理, 实现在特定时间范围内快速准确计算出风场轮廓线。鉴于所选地区平流层20 km附近东西方向风速呈现明显的空间相关性和周期性, 在POD方法的基础上, 提出了一种可以对风场进行预测的Fourier模型。
1 基于POD方法的风场建模 POD方法是指从一组庞大的数据中获得一组低维最优基, 而这组低维最优基是一种能够表示原复杂系统的降阶模型。也就是说POD方法是一种降维的方法, 对给定的数据进行最优的低维逼近, 用较小的维数将原物理模型的主要特征表现出来[13]。本文通过POD方法获得风场信息的最优标准正交基, 将风场数据中的每个风场信息投影到标准正交基上, 获得每个风场数据在标准正交基上的投影系数[14]。并通过最优标准正交基与相对应的投影系数计算出一组新的数据, 将原风场数据的主要特征表现出来。
1.1 瞬像矩阵的生成 瞬像也称为快照, 由Sirovich提出[15], 是指物理场的数值解在不同时刻的空间分布值。建立海拔高度h1至hL的风场模型, 取瞬像矩阵为
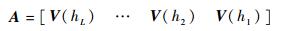 | (1) |
式中:V为风速; 下标L为瞬像时刻数或快照数。假设风场模型统计天数为M, 则A∈RL×M, 一般由试验、经验、统计等方法获得, 通常M?L。
1.2 POD模态的获取 POD模态又称为POD基。POD方法的目的是寻找一组最优的POD基φ1, φ2, …, φr(φi为列向量), 使得数据模型中任意一天特定时刻的风场可以表示为POD基的线性组合[16], 即
 | (2) |
式中:αi(t)为POD基的系数, i=1, 2, …, r。为了寻求满足式(2)的最优POD基, 定义相关矩阵:
 | (3) |
则R∈RL×L, 求取相关矩阵R的非零特征值以及特征向量φi:
 | (4) |
将特征向量化为最优POD基:
 | (5) |
且φi(i=1, 2, …, n; n≤L)是一组标准正交基, 即
 | (6) |
只选取前r阶模态, POD模态矩阵[17]记为
 | (7) |
投影系数矩阵记为
 | (8) |
则降阶模型矩阵B=ΦΩ∈RL×M。
1.3 降阶模型误差评估 POD模态表示捕获物理场的主要特征, 截断后的前r阶POD模态较全阶模态所捕获的能量比为
 | (9) |
故定义相对截断误差[18]为
 | (10) |
2 基于Fourier级数的风场预测模型 通过第1节的POD方法够获得风场数据在最优POD基上的投影系数, 若具有明显的空间相关性和周期性, 可以使用Fourier级数直接进行表示。通过最优POD基与Fourier级数所表示的投影系数计算出特定高度的风速随时间变化情况[19]。其方程表示如下:
 | (11) |
式中:t为时间, d; m为Fourier级数展开的项数; aki和bki为Fourier系数; T为投影系数的振荡周期。
3 实例分析与结果 以长沙地区为例, 采用2005年1月1日—2009年12月31日每天00:00所测量的风场数据, 风场数据由国防科技大学气象海洋学院提供, 数据记录了长沙地区00:00和12:00(世界时)的风速、湿度、温度、气压等气象要素, 数据覆盖海拔高度0~60 km之间每隔0.5 km所对应的天气数据。考虑到临近空间低动态飞行器驻空期间的工作高度范围, 本文针对海拔高度10~30 km的范围进行研究, 并通过3次样条对风场数据进行了插值处理。
3.1 风场建模与预测 相对模态能量分布主要用于识别数据降阶处理所需的模态数量。图 1(a)给出了东西方向风场各阶POD模态的相对模态能量, 前5种模态能量所占的比重相对于其他模态能量具有明显的区别, 可以捕获到风场总特征性的98.9%。同时, 由图 1(b)可知, 南北方向风场的相对模态能量分布除前2种模态之外, 其余模态能量呈逐渐下降的趋势, 若只选取前2种模态进行降阶处理, 不足以表现出风场的主要特征。因此, 南北方向风场不能高效地进行降阶建模。
 |
| 图 1 相对模态能量分布 Fig. 1 Relative mode energy distribution |
| 图选项 |
通过选用多种POD模型分别对2007年11月6日0:00时刻东西方向和南北方向的风场进行建模。由图 2(a)可知, 10阶和15阶POD模型较好地表示出东西方向风场的实际数据, 5阶POD模型能体现出东西方向风场的主要特征。图 2(b)中实际风场模型清楚地表明南北方向风速随空间的变化是极其不规则的, 导致南北方向风场的低阶重建性较差。因此, 低阶的POD模型(比如5阶)在捕获东西方向风场数据的总体趋势上是有效的。
 |
| 图 2 采用POD方法重建风场 Fig. 2 Reconstruction of wind field using POD method |
| 图选项 |
经过POD方法降阶处理后可以得到相对应的投影系数。以第一阶POD模态的投影系数Ck1为例, 通过Fourier级数拟合, 可以得出其Fourier预测模型, 分别从东西方向(见图 3)和南北方向(见图 4)进行分析。从图 3(a)和图 4(a)可看出, 两者的投影系数Ck1都具有周期性和规律性, 都能够通过Fourier级数将其拟合(分别见图 3(b)和图 4(b))。但相对于南北方向风场, 东西方向风场的投影系数更紧密, 周期性更强, Fourier级数的拟合程度更高, 说明东西方向风场更适用于建立Fourier预测模型。
 |
| 图 3 系数拟合(东西方向) Fig. 3 Coefficient fitting (east-west direction) |
| 图选项 |
 |
| 图 4 系数拟合(南北方向) Fig. 4 Coefficient fitting (north-south direction) |
| 图选项 |
利用东西方向风场的Fourier预测模型, 可以获得某一天特定时刻下的投影系数, 能对该时刻下平流层20 km附近的东西方向风速随高度的变化情况进行预测。如图 5所示, 以2008年11月7日为例, 5阶POD模型能够捕获到实际风场的主要特征, Fourier预测模型能够体现出5阶POD模型的整体变化趋势状况。
 |
| 图 5 各种方法下风矢量图的比较 Fig. 5 Comparison of wind vector plots for various methods |
| 图选项 |
将Fourier预测模型向外延伸和扩展, 可以对未来特定时刻下的风场进行预测。通过2005—2009年风场数据的统计和分析, 对2010年10月30日0:00平流层20 km附近的东西方向风速进行预测, 结果如图 6所示, Fourier预测模型能预测到风速随高度的变化情况, 并且能够体现出平流层低速风带所在的位置高度。
 |
| 图 6 实际风矢量图与预测风矢量图的对比 Fig. 6 Comparison of actual wind vector with predicted wind vector plots |
| 图选项 |
3.2 Fourier预测精度分析 由图 5、图 6可知, 针对不同的高度, Fourier预测模型与实际风场模型之间存在不同的偏差, 说明Fourier预测精度与空间分布有关, 下面通过模型之间的比较, 对Fourier预测精度进行分析。
将图 5中3种风场模型分别进行比较, 如图 7(a)所示, 其中POD降阶残差表示5阶POD风场模型与实际风场之差, Fourier拟合残差表示Fourier级数进行拟合时与5阶POD模型之差, Fourier预测残差表示Fourier预测模型与实际风场之差。由图 7(a)可知, 3种残差的绝对值都小于5, 其中POD降阶残差曲线的差波动性最小, 说明5阶POD模型与实际风场模型数据很接近。由于Fourier预测模型是基于POD方法降阶处理后建立的, 所以Fourier预测残差等于POD降阶残差与Fourier拟合残差两者之和, 说明Fourier预测精度不仅与POD降阶模型所捕获到的能量有关, 而且和Fourier级数的拟合程度有关。将图 6中Fourier预测模型与实际风场模型进行比较, 如图 7(b)所示, Fourier预测残差曲线的波动范围较小, 在海拔高度19~22 km之间的残差接近于0, 说明在此范围内, Fourier预测精度较高, 而在15 km附近波动最大, 说明预测精度较低。
 |
| 图 7 残差分析 Fig. 7 Residual analysis |
| 图选项 |
由图 7可知, 在20 km处Fourier预测精度相对较高, 在15和24 km处的预测精度较低。分别对15、20和24 km, 3个高度的东西方向风速随时间的变化情况进行分析, 并分别计算出实际风场模型、5阶POD模型与Fourier预测模型两两之间的残差, 结果如图 8、图 9所示。由图 9可知, 在这3个高度位置上, POD降阶残差都接近于零, 说明对于5阶POD模型, 在任意高度上都能够捕获到实际风场的主要特征; 对于Fourier预测模型, 如图 8所示, 在20 km处东西方向的风场数据相对于其他2个高度的数据更加紧凑、平稳, Fourier级数的拟合程度也更高, 说明Fourier预测模型与实际风场随时间变化的紧凑性与规律性有着密切联系, 风场数据越紧凑, 周期性越明显, Fourier预测精度就越高。
 |
| 图 8 不同高度的风速变化情况 Fig. 8 Change of wind speed at different altitudes |
| 图选项 |
 |
| 图 9 不同高度的残差分析 Fig. 9 Residual analysis at different altitudes |
| 图选项 |
4 结论 本文通过POD方法将平流层风场数据进行高精度高效率降阶处理后, 为Fourier预测模型对风场进行预测节省了大量的计算时间, 大大提高了计算效率, 得到:
1) 提出了一种对平流层风场数据进行降阶处理的POD方法, 在POD方法的基础上, 提出了一种可以对平流层风场进行预测的Fourier预测模型。
2) 以长沙地区为例, 选取海拔高度10~30 km的5年风场数据, 采用提出的POD方法与Fourier预测模型对风场进行了建模与预测, 并对Fourier预测精度进行了分析。
3) 研究结果表明:采用POD方法可以对东西方向风场进行高效高精度的降阶建模, 由于南北方向风场变化极其不规则, 不可以采用低阶的POD模型进行建模; 通过Fourier预测模型能对东西方向风场进行准确预测, 预测精度与实际风场随时间变化的规律性有关, 风场数据越紧凑, 周期性越明显, Fourier预测精度越高。
参考文献
| [1] | 王彦广, 李健全, 李勇, 等. 近空间飞行器的特点及其应用前景[J].航天器工程, 2007, 16(1): 50–57. WANG Y G, LI J Q, LI Y, et al. The characteristics of spacecraft and its application prospect[J].Spacecraft Engineering, 2007, 16(1): 50–57.DOI:10.3969/j.issn.1673-8748.2007.01.010(in Chinese) |
| [2] | 陶梦初, 何金海, 刘毅. 平流层准零风层统计特征及准两年周期振荡对其影响分析[J].气候与环境研究, 2012, 17(1): 92–102. TAO M C, HE J H, LIU Y. Study on the statistical characteristics of the quasi-zero wind stratosphere and the influence of quasi-two-year periodic oscillations on the stratosphere[J].Climate and Environment Research, 2012, 17(1): 92–102.DOI:10.3878/j.issn.1006-9585.2011.10087(in Chinese) |
| [3] | SHANG L, LIU Y, WANG Y, et al. Seasonal distribution of ozone and radiation field at the stratosphere[J].Chinese Journal of Space Science, 2015, 504(3): 213–217. |
| [4] | 王文龙.大气风场模型研究及应用[D].长沙: 国防科学技术大学, 2009. WANG W L.Study and application of atmospheric wind field model[D].Changsha: National University of Defense and Technology, 2009(in Chinese). |
| [5] | DAN R, HUA H, CASTAN~óN D A, et al. Normalized proper orthogonal decomposition (NPOD) for building pressure data compression[J].Journal of Wind Engineering & Industrial Aerodynamics, 2006, 94(6): 447–461. |
| [6] | HOLMES J D, SANKARAN R, KWOK K C S, et al. Eigenvector modes of fluctuating pressures on low-rise building models[J].Journal of Wind Engineering & Industrial Aerodynamics, 1997, 69-71: 697–707. |
| [7] | FIC A, BIALECKI R A, KASSAB A J. Solving transient nonlinear heat conduction problems by proper orthogonal decomposition and the finite-element method[J].Numerical Heat Transfer Part B Fundamentals, 2005, 48(2): 103–124.DOI:10.1080/10407790590935920 |
| [8] | TAN B T, DAMODARAN M, WILLCOX K E. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J].AIAA Journal, 2004, 42(8): 1505–1516.DOI:10.2514/1.2159 |
| [9] | 胡亮.基于特征正交分解的桥梁风场随机模拟[D].武汉: 华中科技大学, 2007. HU L.Study on stochastic simulation of bridge wind field based on characteristic orthogonal decomposition[D].Wuhan: Huazhong University of Science and Technology, 2007(in Chinese). |
| [10] | 陶青秋.本征正交分解(POD)方法在建筑风荷载及其动态响应中的应用研究[D].汕头: 汕头大学, 2002. TAO Q Q.Application of the proper orthogonal decomposition (POD) method in building wind load and its dynamic response[D]. Shantou: Shantou University, 2002(in Chinese). |
| [11] | 邹垚, 梁枢果, 邹良浩. 基于本征模态修正的POD法在风场重建中的应用[J].土木工程学报, 2010, 43(s1): 305–309. ZOU Y, LIANG S G, ZOU L H. Application of POD method based on eigen modification in wind field reconstruction[J].China Civil Engineering Journal, 2010, 43(s1): 305–309.(in Chinese) |
| [12] | CHEN X, KAREEM A. Proper orthogonal decomposition-based modeling, analysis, and simulation of dynamic wind load effects on structures[J].Journal of Engineering Mechanics, 2005, 131(4): 325–339.DOI:10.1061/(ASCE)0733-9399(2005)131:4(325) |
| [13] | CHATTERJEE A. An introduction to the proper orthogonal decomposition[J].Current Science, 2000, 78(7): 808–817. |
| [14] | EVERSON R, SIROVICH L. Karhunen-Loeve procedure for gappydata[J].Journal of the Optical Society of America A, 1995, 12(8): 1657–1664.DOI:10.1364/JOSAA.12.001657 |
| [15] | SIROVICH L. Turbulence and the dynamics of coherent structures Part Ⅰ:Coherent structures[J].Quarterly of Applied Mathematics, 1986, 45(3): 561–571. |
| [16] | KUNISCH K. Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics[J].SIAM Journal on Numerical Analysis Archive, 2002, 40(2): 492–515.DOI:10.1137/S0036142900382612 |
| [17] | 胡金秀, 郑保敬, 高效伟. 基于特征正交分解降阶模型的瞬态热传导分析[J].中国科学:物理学力学天文学, 2015, 45(1): 014602. HU J X, ZHENG B J, GAO X W. Virtual overtemperature analysis based on reduced order model of characteristic orthogonal decomposition[J].Chinese Science:Physics, Astronomy, 2015, 45(1): 014602.(in Chinese) |
| [18] | 杜娟.流体力学方程基于POD方法的降维数值解法研究[D].北京: 北京交通大学, 2011. DU J.Research on decreasing numerical solution of fluid dynamics equations based on POD method[D].Beijing: Beijing Jiaotong University, 2011(in Chinese). |
| [19] | HEIKKIL?U, SHI X, PHIPPS S J, et al. 10Be in late deglacial climate simulated by ECHAM5-HAM-Part 2:Isolating the solar signal from 10Be deposition[J].Climate of the Past Discussions, 2013, 9(5): 5627–5657.DOI:10.5194/cpd-9-5627-2013 |
