针对波纹板的力学性能,Nguyen等[1-3]运用实验和传统有限元的方法分析了波纹板的成形过程、拉伸性能和三点弯曲性能。波纹板具有优异的性能,近年来Kim等针对波纹板的力学性能[4-5],Nguyen等针对波纹板成形后结构件(C型钢[6-7]、方型钢[8])的力学性能,Labergere等针对波纹板冲压成形过程[9]等进行了分析,研究表明各种形式的波纹板均展现出优异的性能。
由于波纹板复杂的形貌特点,其宏观刚度特性难以通过弹塑性理论解析的方法得到;而传统有限元的数值模拟手段则需要大量的网格表征板材表面形貌,计算效率低、误差大,难以得到板材刚度特性与其表面形貌结构参数之间的准确关系。分析波纹板的结构特征可以发现,板材的宏观结构由单胞结构平移阵列得到,通过对单胞结构施加周期性边界条件可得到结构的宏观力学特性和应力分布情况[10-11]。为保证单胞结构任意方向的变形协调和应力连续,众多****对周期性边界条件的数学表达式和有限元实现进行研究[12-15],该方法已经在纺织复合材料等领域得到广泛应用。对于只在2个方向具有周期排布特点的板材,需要释放一个方向的约束,Sankar和Marrey对传统的周期性边界条件进行改进[16],实现了对层合板[17]、瓦楞板[18-19]等只在2个方向具有周期排布特点板材的力学性能分析。因此,利用单胞有限元的方法可以更加准确、高效地得到波纹板的等效刚度特性,获得板材表面形貌结构参数与其刚度特性之间的准确关系,实现面向使用需求的板材形貌设计。
基于以上分析,本文首先建立波纹板单胞有限元模型,实现了基于单胞有限元模型的板材等效刚度特性的求解;随后对典型形貌的铝波纹板的等效刚度特性进行分析验证;最后基于单胞模型得到了波纹板结构参数对等效刚度特性的影响规律。
1 单胞有限元模型及等效刚度特性 1.1 单胞的选取及变形假设条件 波纹板整体形貌如图 1(a)所示,选取的单胞结构如图 1(b)所示,其主要结构参数包括波纹板厚度h,单胞结构的周期间距p,以及基础薄板的厚度t,如图 1(c)所示。本文波纹板在x、y方向具有相同的周期间距及形貌。
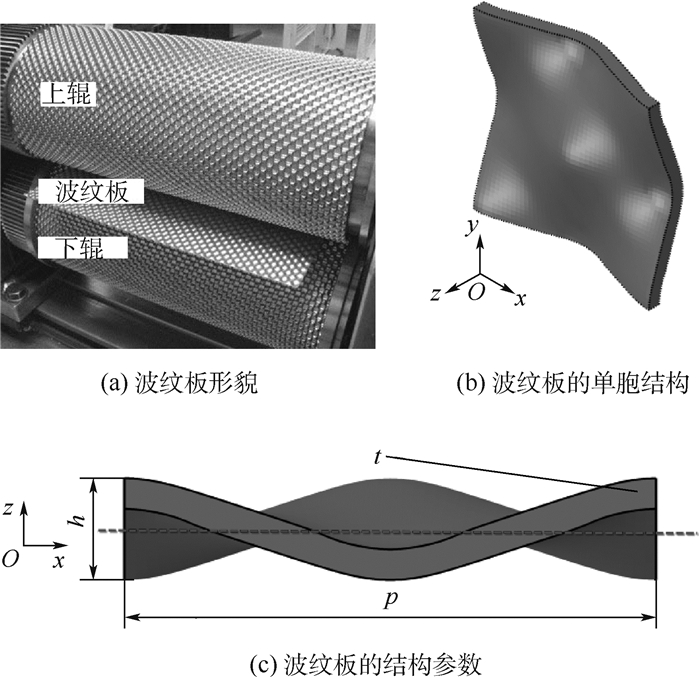 |
| 图 1 波纹板单胞的选取及结构参数 Fig. 1 Selection and structural parameters of dimpled sheet unit cell |
| 图选项 |
为使用单胞有限元模型分析波纹板的等效刚度特性,波纹板的结构需具有周期排布和弹性小变形的特性。分析波纹板的结构特点可以发现,其宏观结构满足如下5个假设:
1) 波纹板的厚度远小于宏观结构的长度和宽度。
2) 波纹板的弹性弯曲问题符合小挠度理论。
3) 波纹板在宏观上呈现出均质各向异性的特点。
4) 单胞结构具有相同的应力场和应变场。
5) 波纹板的中面与其几何中性层重合,即图 1(c)中的虚线位置。
因此,波纹板满足使用单胞有限元方法进行等效刚度特性分析的条件。
1.2 单胞周期性边界条件的有限元实现 根据周期边界条件的建立条件,单胞结构的周期性边界条件需保证结构的变形协调和应力连续[15]。现对波纹板单胞模型的周期边界条件分析如下。
1.2.1 变形协调条件的实现 选取图 1(b)中的单胞结构的轮廓,如图 2所示。
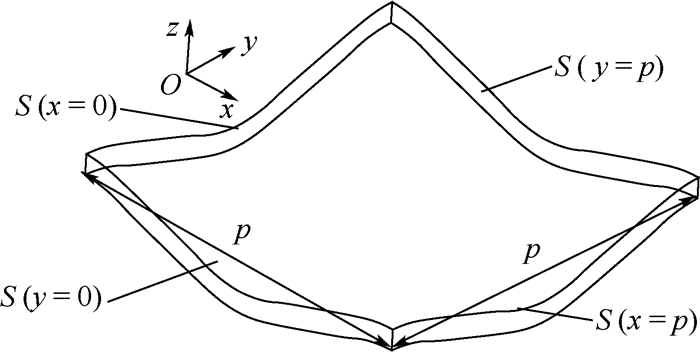 |
| 图 2 单胞结构轮廓示意图 Fig. 2 Schematic diagram of unit cell profile |
| 图选项 |
根据Sharma等[19]分析的单胞结构平均应变与节点位移之间的关系,在波纹板单胞模型的平行对面即S(x=p)、S(x=0)和S(y=p)、S(y=0)中对应节点之间的位移和应变关系为
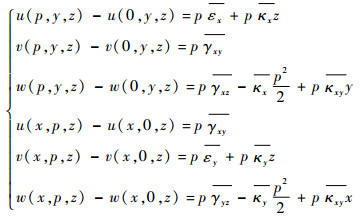 | (1) |
式中:u、v和w分别为对应节点在x、y和z方向的位移;
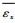
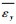
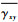
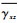
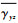
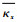
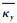
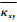
由于横向剪切应变
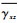
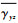
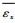
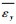
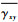
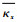
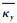
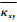
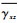
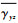
表 1 单胞结构6种单位应变载荷的周期性边界条件 Table 1 Periodic boundary condition for six unit strain loads of unit cell
| 应变 | u(p, y, z)-u(0, y, z) | v(p, y, z)-v(0, y, z) | w(p, y, z)-w(0, y, z) | u(x, p, z)-u(x, 0, z) | v(x, p, z)-v(x, 0, z) | w(x, p, z)-w(x, 0, z) |
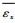 =1 =1 | p | 0 | 0 | 0 | 0 | 0 |
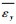 =1 =1 | 0 | 0 | 0 | 0 | p | 0 |
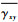 =1 =1 | 0 | p/2 | 0 | p/2 | 0 | 0 |
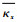 =1 =1 | pz | 0 | -p2/2 | 0 | 0 | 0 |
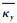 =1 =1 | 0 | 0 | 0 | 0 | pz | -p2/2 |
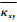 =1 =1 | 0 | pz/2 | -py/2 | pz/2 | 0 | -px/2 |
表选项
1.2.2 应力连续条件的实现 在基于位移的有限元分析中,由于应力边界条件是通过最小势能原理自动满足的,这类边界条件为自然边界条件,即只需对单胞结构施加位移边界条件就可以保证所得结果的唯一确定性[15],从而保证应力的连续性,即平行面的对应节点所受力大小相等方向相反,如下所示:
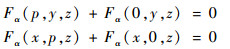 | (2) |
式中:F为对应节点所受的力;α=x, y, z分别代表所受力的方向。
1.3 等效拉伸刚度和等效弯曲刚度特性的计算 1.2节实现了波纹板单胞结构有限元模型的建立,本节将基于单胞有限元模型的输出结果建立板材等效刚度特性的计算方法。根据复合材料力学[20]中对刚度特性的定义,波纹板等效刚度特性可写为
 | (3) |
式中:A为拉伸刚度系数;D为弯曲刚度系数;AQ为剪切刚度系数;N为平面内单位宽度的拉力;M为单位宽度内的力矩;Q为单位宽度内的横向剪力。
由式(3)可知,分别给波纹板单胞结构施加如表 1所示的6种应变载荷,从有限元软件中读取周期边界上每个节点所受的力可求得单胞结构的内力数值为
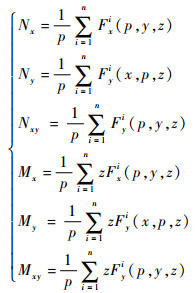 | (4) |
通过式(3)和式(4)可计算得到波纹板的等效拉伸刚度系数A和等效弯曲刚度系数D。
1.4 等效剪切刚度的计算 波纹板截面形貌的变化使得横向剪切应力引起的变形增加,若对单胞模型直接施加剪切应变对应的周期性边界条件,会产生附加弯矩,等效剪切刚度计算误差较大,因此不能通过以上单胞模型解决。针对这一问题,Ravishankar[17]和Sharma[19]等通过对单胞结构组成的多胞简支梁施加均布载荷的方法,通过位移响应和弯曲刚度计算得到了板的等效剪切刚度。本节基于该方法建立波纹板等效剪切刚度的计算模型。
将单胞结构在x方向进行10次阵列,可得到总长为L=10p的梁结构,对S(x=0)面进行固定,S(y=0)和S(y=p)面进行面内位移的约束,在顶面施加均布载荷P0,如图 3所示。根据剪切变形板理论可知自由端的挠度值计算式为[21]
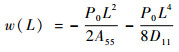 | (5) |
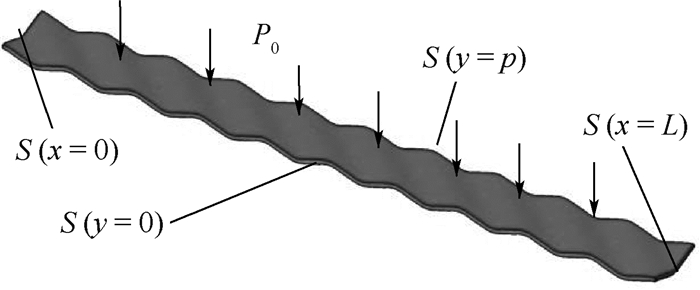 |
| 图 3 波纹板单胞结构组成的梁结构 Fig. 3 Cantilever plate with unit cells of dimpled sheet |
| 图选项 |
波纹板在2个方向具有相同的形貌和间距,因此其2个方向的剪切刚度A44=A55。建立上述有限元模型,可以从有限元软件中得到自由端的位移响应w(L)0。将1.3节中计算得到的等效弯曲刚度D11代入式(5),即可计算得到波纹板的等效剪切刚度为
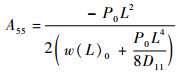 | (6) |
2 波纹板等效刚度特性的计算及验证 为了讨论和分析典型形貌波纹板的刚度特性,同时对单胞模型计算等效刚度特性的方法进行验证。选取结构参数为h=1.6 mm,p=8 mm,t=0.5 mm的波纹板作为研究对象,计算并验证单胞模型的正确性。
2.1 波纹板形貌特征的提取 波纹板表面形貌采用普通薄板滚压塑性成形加工而成,因此其单胞形态和厚度变化无法采用简单的数学函数进行描述,必须使用数值模拟薄板成形过程,才能提取准确的波纹板实际形貌。针对波纹板周期排布的特点,若对其整个滚动成形过程进行仿真需要大量的单元和计算时间,效率极低。由于该成形辊直径远大于薄板的厚度,文献[2, 22]中对波纹板的成形过程均进行了简化,仅对单胞模型成形过程进行数值模拟,得到单胞的形貌与实际形貌相近,可作为刚度特性分析的单胞形貌结构。
运用ABAQUS软件对单胞结构的成形过程进行数值模拟,选取成形冲头半径R=2.5 mm,周期间距p=8 mm,板材厚度t=0.5 mm,最终厚度h=1.6 mm的铝波纹板进行分析。单胞模型由15 000个C3D8R单元组成,弹性模量E=69 000 MPa,泊松比ν=0.33,材料工程应力应变曲线根据金属拉伸实验方法[23]得到,真实应力应变曲线如图 4(a)所示。
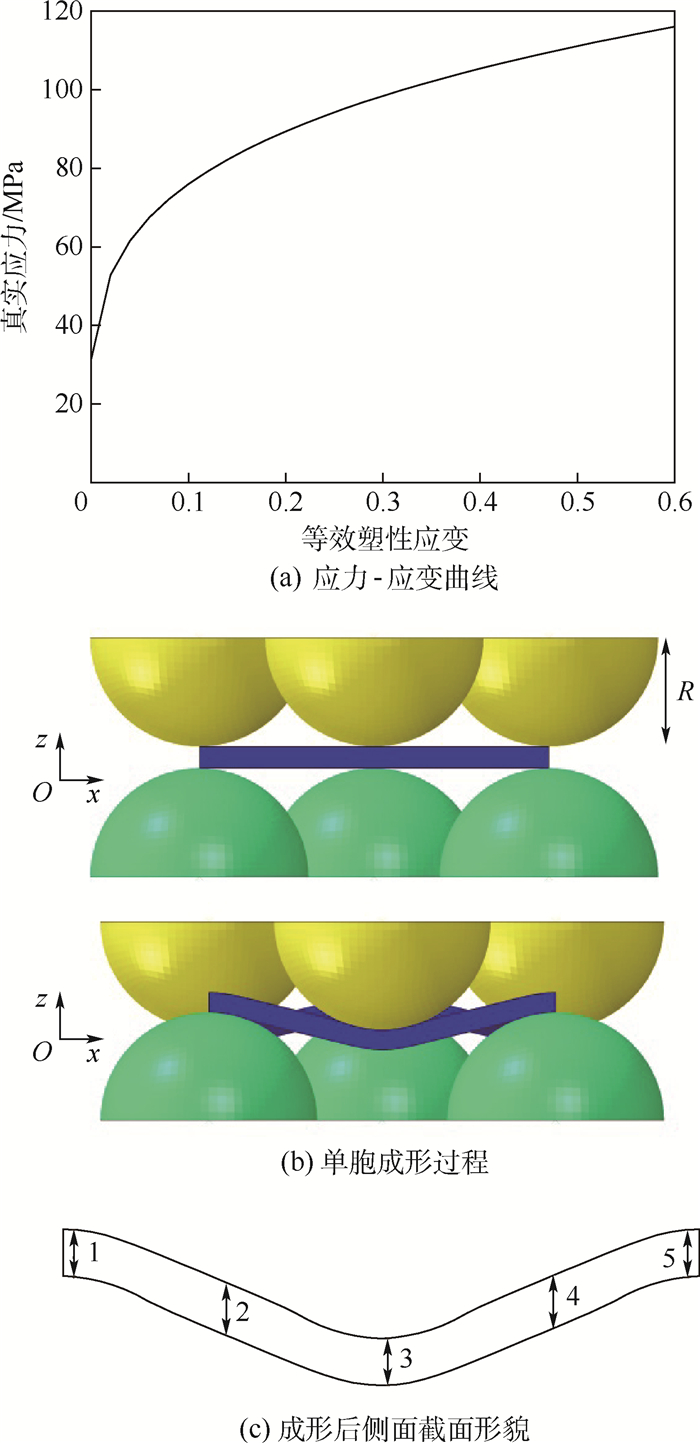 |
| 图 4 波纹板单胞形貌的提取 Fig. 4 Unit cell morphology extraction of dimpled sheet |
| 图选项 |
单胞结构成形的有限元模型如图 4(b)所示,成形数值模拟结束后对其进行回弹分析,即可得到波纹板单胞的最终形貌,成形结果即为波纹板的单胞结构,其中变形最大截面的形貌如图 4(c)所示。模拟结果与实际观测结果相似,上述结构尺寸的波纹板成形后部分位置发生减薄,在冲头顶点位置减薄量最大为8%,如图 4(c)中1、3、5位置,与冲头不接触位置有小量的减薄,约为2%,如图 4(c)中2、4位置。
2.2 等效刚度特性计算
2.2.1 等效拉伸刚度和等效弯曲刚度 普通板经过加工后可形成波纹板,由于塑性变形,局部会产生加工硬化,但不影响材料的弹性常数。等效刚度指板材抵抗弹性变形的能力,在变形过程中不考虑材料的塑性段,因此在等效刚度计算中只需输入铝的弹性模量和泊松比。
在2.1节中得到的单胞结构的形貌,对其分别施加表 1所示的6种应变载荷的周期性边界条件,根据计算结果文件得到等效内力并计算波纹板的等效拉伸和弯曲刚度特性。单胞结构在6种边界条件下的应力分布如图 5所示。
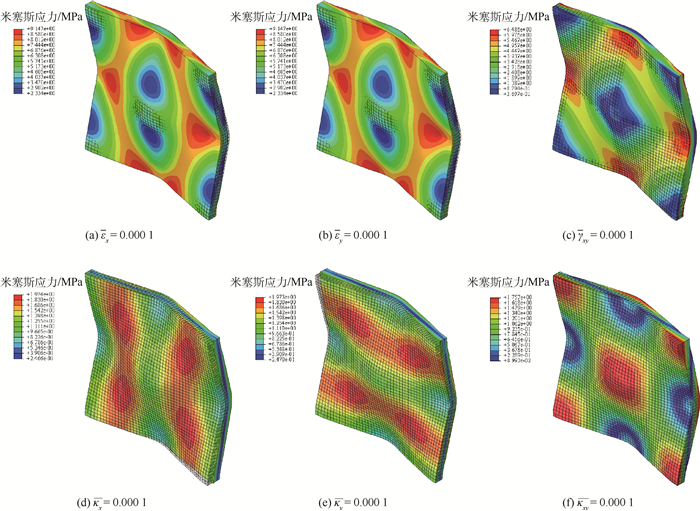 |
| 图 5 单胞结构在6种变形情况的应力云图 Fig. 5 Stress contours of unit cell in six deformation cases |
| 图选项 |
根据经典薄板理论,厚度为t的基础薄板的刚度特性可由式(7)和式(8)计算:
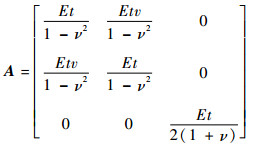 | (7) |
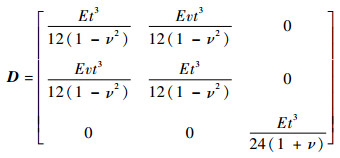 | (8) |
分析表 2可知,与基础薄板相比,波纹板的拉伸刚度普遍降低,并且出现负泊松比的现象,而弯曲刚度则有不同程度的提升。图 6所示为波纹板板与基础薄板单胞结构在相同拉伸应变时的应力分布情况。可以看出,拉伸过程中波纹板的应力分布并不均匀;在板材凸凹的部位其应力较小,并未完全承担到拉伸载荷,而拉伸载荷则主要由波纹板应力较大区域负担,因此,波纹板的拉伸刚度比基础板材产生了降低。而对于波纹板弯曲刚度的提升,则是由于加工后波纹板的厚度达到了基础板材的3.4倍,材料截面形貌变得复杂,使得波纹板的等效弯曲刚度提升,厚度的增加使得波纹板相对密度降低,实现了结构轻量化。
表 2 波纹板与基础薄板的刚度特性 Table 2 Stiffness properties of dimpled sheet and base flat sheet
| 刚度 | 波纹板 | 基础薄板 | 波纹板与基础薄板刚度比值 |
| A11/(N·mm-1) | 24 069 | 38 716 | 0.622 |
| A12/(N·mm-1) | -162 | 12 776 | -0.013 |
| A22/(N·mm-1) | 24 069 | 38 716 | 0.622 |
| A66/(N·mm-1) | 6 558 | 12 970 | 0.506 |
| D11/(N·mm) | 1 015 | 806 | 1.26 |
| D12/(N·mm) | 517 | 266 | 1.944 |
| D22/(N·mm) | 1 015 | 806 | 1.26 |
| D66/(N·mm) | 1 165 | 270 | 4.315 |
表选项
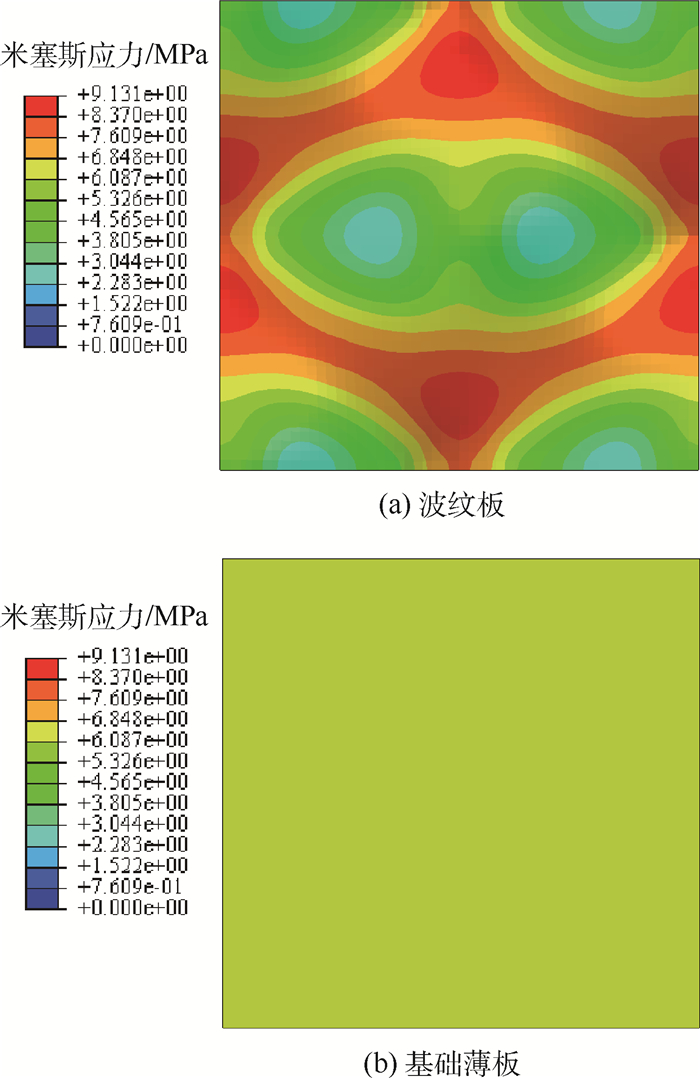 |
| 图 6 单胞在单向拉伸时的应力分布 Fig. 6 Stress distribution of unit cell under uniaxial tension |
| 图选项 |
2.2.2 等效剪切刚度 L=80 mm,P0=1×10-3 MPa时,由式(6)计算得到等效剪切刚度,梁结构自由端挠度值w(L)0可由有限元仿真结果得到,根据已经计算得到的D11可以计算得到等效剪切刚度A44=A55=88N/mm。
2.3 波纹板刚度特性验证 为验证单胞模型计算结果的正确性,分别建立实体三维模型和以单胞模型等效刚度计算结果为基础的等效壳单元模型进行数值模拟,其中实体模型采用将单胞结构分别在x方向和y方向进行10次复制的方式建立。在两模型中将板的边界进行简支,承受P0=0.001 MPa的压强载荷,在该种载荷情况下波纹板中的各刚度分量都会对最终位移响应产生影响,适合于等效模型的验证。由于对称性建立1/4模型,边界条件及载荷情况如图 7(a)所示,以x方向坐标为横坐标,z方向位移为纵坐标,对比2种情况下的位移响应,如图 7(b)所示。
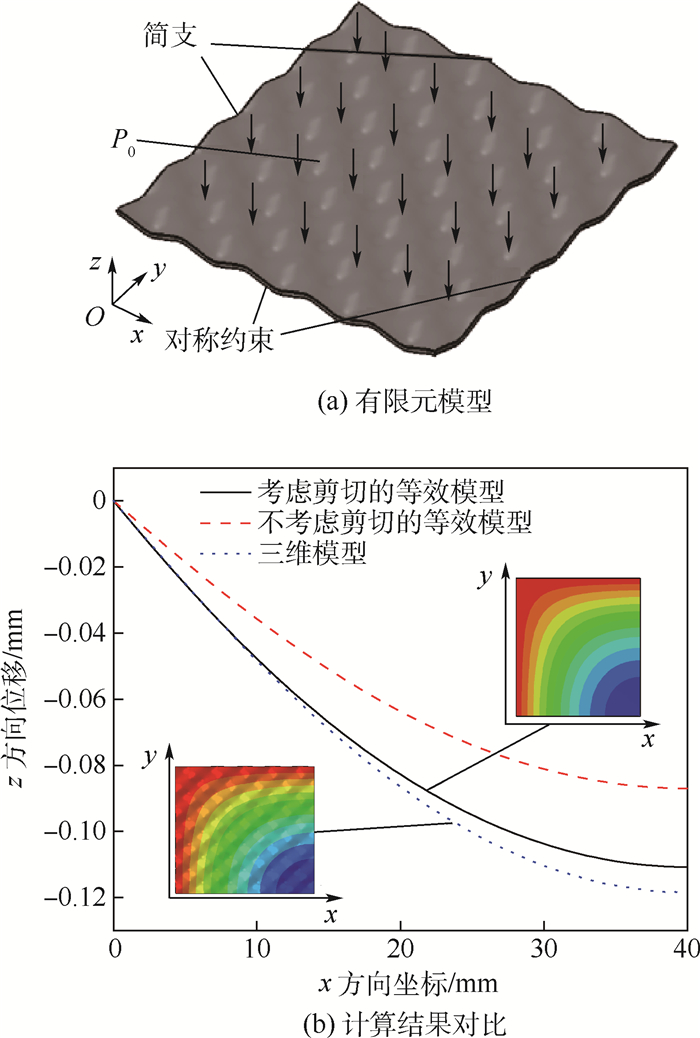 |
| 图 7 等效模型的验证 Fig. 7 Verification of equivalent model |
| 图选项 |
由图 7(b)可知,不考虑剪切刚度的模型与三维实体模型误差较大;考虑剪切的等效模型与三维实体模型在z方向具有相近的位移响应,最大误差在6%。在上述模型中,实体三维模型需建立37.5万个C3D20R单元,计算时间为6 000 s,等效模型仅需要6 400个S4R单元,计算时间仅为1 s,计算效率大大提升,适用于任意形貌的波纹板的不同载荷情况下的位移响应计算。因此运用单胞有限元方法对波纹板等效刚度特性的分析是有效的,得到的等效刚度特性可计算波纹板在不同载荷情况下的位移响应,极大地提高了计算效率,从而可以实现以波纹板为基础材料的复杂构件位移响应的计算。
3 结构参数对等效刚度特性的影响 讨论过程中首先对波纹板的结构参数及其等效刚度特性进行无量纲化。因变量为对应等效刚度特性与基础薄板的刚度特性的比值,自变量以基础薄板厚度t为基准,讨论p/t和h/t对波纹板等效刚度特性的影响规律,其中h/t可视为波纹板的相对厚度,p/t可视为波纹相对周期间距。
3.1 不同结构参数对波纹板形貌的影响 在2.1节中已给出了波纹板形貌的提取方法,通过成形过程的数值模拟可得到不同结构参数波纹板单胞结构的形貌,如图 8所示。分析表明,结构参数的变化使得波纹板最终的形貌特征不同,h/t的增加使得波纹板最大减薄率由6%增大到10%,而p/t的变化只对波纹周期长度产生影响,对最大减薄量基本没有影响。
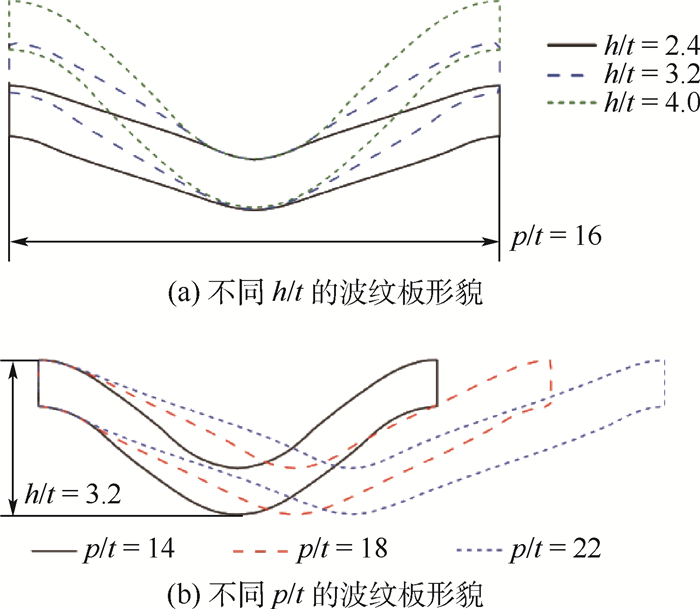 |
| 图 8 不同结构参数波纹板单胞结构的形貌 Fig. 8 Morphology of unit cell of dimpled sheet with different structural parameters |
| 图选项 |
3.2 相对厚度对刚度特性的影响 图 9为p/t=16,h/t=2.4~4.0时波纹板等效刚度特性的变化规律。可以看出,当h/t由小变大时,即波纹板的相对厚度增大时,其拉伸刚度和剪切刚度持续降低,弯曲刚度不断提升。如图 9(a)所示,当A12为负值时波纹板出现负泊松比,与Javid等[24]的发现相似。
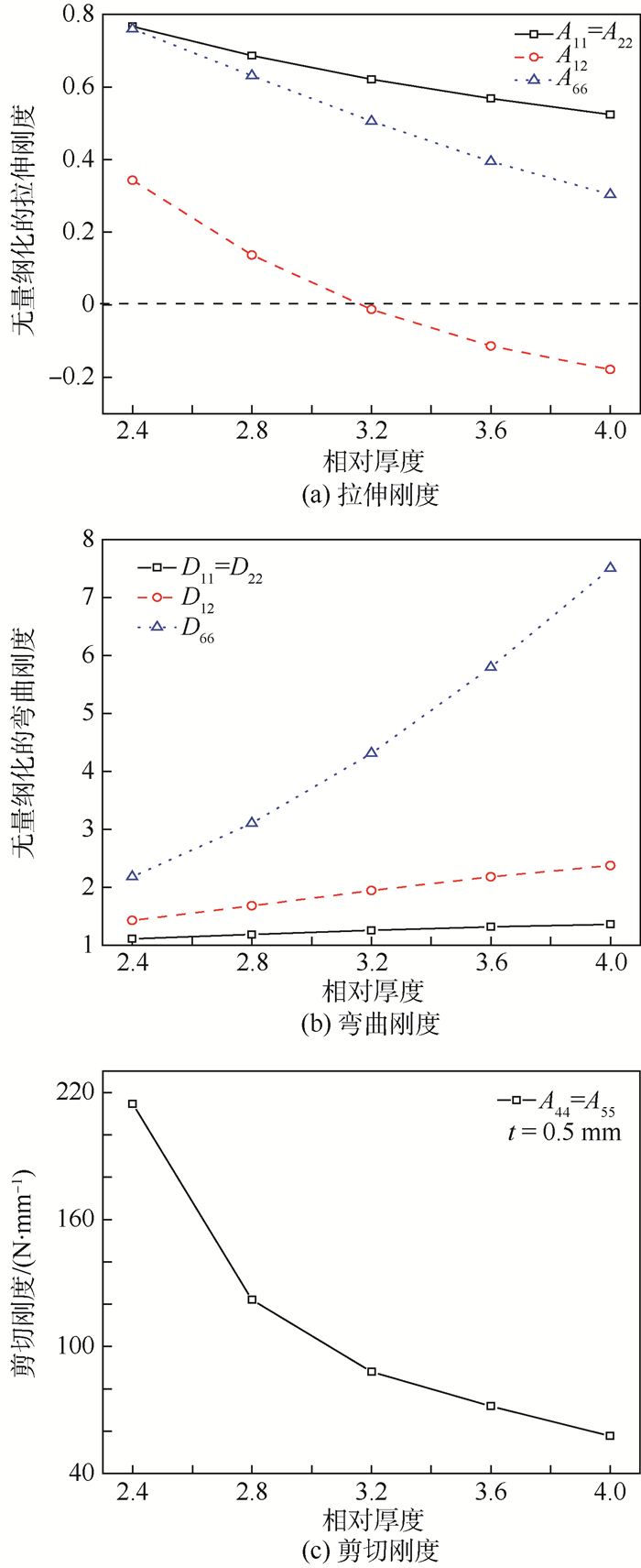 |
| 图 9 相对厚度对等效刚度特性的影响 Fig. 9 Effect of h/t on equivalent stiffness property |
| 图选项 |
3.3 相对周期间距对刚度特性的影响 图 10为h/t=3.2,p/t=14~24时波纹板的等效刚度特性变化规律。可以看出,当p/t由小变大时,即波纹板的波纹周期变长时,其拉伸刚度和剪切刚度逐渐提升,弯曲刚度逐渐降低。分析形成这一规律的原因如图 8(b)所示,当h/t固定时,随着p/t的增大使得单胞结构的形貌更趋近于基础薄板,其性能也逐渐趋向于基础薄板,从而使拉伸刚度和剪切刚度提升,弯曲刚度降低。
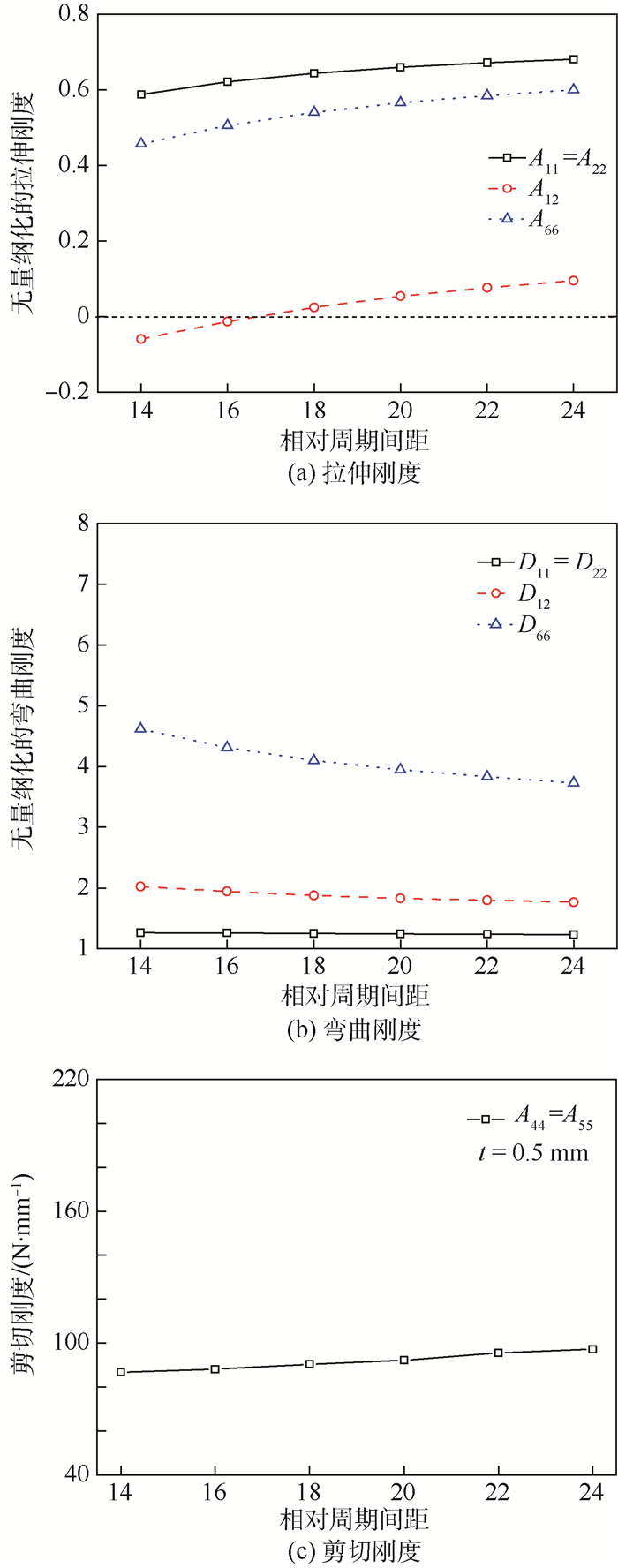 |
| 图 10 相对厚度对刚度特性的影响 Fig. 10 Effect of p/t on equivalent stiffness property |
| 图选项 |
4 结论 1) 通过建立波纹板单胞结构周期性边界条件及应变载荷的计算方法,得到了波纹板的等效刚度特性。该方法计算效率高、数值准确,可以实现以波纹板为基础材料的复杂构件位移响应的计算。
2) 对典型形貌的波纹板等效刚度特性的分析表明,普通薄板经过滚压加工后截面形貌趋于复杂,波纹板相对厚度增加导致其弯曲刚度提升,而在受拉伸载荷时的应力分布不均导致其拉伸刚度降低。
3) 波纹板的相对厚度和波纹相对周期间距都会影响其等效刚度特性。相对厚度的增加会降低拉伸刚度和剪切刚度,提升波纹板的弯曲刚度;波纹相对周期间距的增加会提升拉伸刚度和剪切刚度,降低波纹板的弯曲刚度。
本文分析了波纹板结构参数对其刚度特性的影响规律,未来结合其结构的隔热、隔声和成形性等性能,可对波纹板的实际应用提供理论依据,使得波纹板在航空航天、船舶重工等领域具有更广泛的应用。
参考文献
| [1] | NGUYEN V B, WANG C J, MYNORS D, et al. Mechanical properties and structural behaviour of cold-roll formed dimpled steel[J].Steel Research International, 2011(Special): 1072–1077. |
| [2] | NGUYEN V B, WANG C J, MYNORS D J, et al. Finite element simulation on mechanical and structural properties of cold-formed dimpled steel[J].Thin-Walled Structures, 2013, 64: 13–22.DOI:10.1016/j.tws.2012.11.002 |
| [3] | NGUYEN V B, WANG C J, MYNORS D J, et al. Dimpling process in cold roll metal forming by finite element modeling and experimental validation[J].Journal of Manufacturing Processes, 2014, 16(3): 363–372.DOI:10.1016/j.jmapro.2014.03.001 |
| [4] | OH S H, AHN D C, KIM Y S. A study on the mechanical properties and springback of 3D aluminum sheets[J].International Journal of Precision Engineering and Manufacturing, 2016, 17(5): 671–677.DOI:10.1007/s12541-016-0082-0 |
| [5] | KIM Y S, OH S H, DO V C, et al. Evaluation of the plastic yield locus for embossed sheet using biaxial tensile tests[J].Metals and Materials International, 2016, 22(6): 974–981.DOI:10.1007/s12540-016-6173-8 |
| [6] | NGUYEN V B, WANG C J, MYNORS D J, et al. Compression tests of cold-formed plain and dimpled steel columns[J].Journal of Constructional Steel Research, 2012, 69(1): 20–29.DOI:10.1016/j.jcsr.2011.07.004 |
| [7] | NGUYEN V B, MYNORS D J, WANG C J, et al. Analysis and design of cold-formed dimpled steel columns using finite element techniques[J].Finite Elements in Analysis and Design, 2016, 108(C): 22–31. |
| [8] | LIANG C, WANG C J, NGUYEN V B, et al. Experimental and numerical study on crashworthiness of cold-formed dimpled steel columns[J].Thin-Walled Structures, 2017, 112: 83–91.DOI:10.1016/j.tws.2016.12.020 |
| [9] | LABERGERE C, BADREDDINE H, MSOLLI S, et al. Modeling and numerical simulation of AA1050-O embossed sheet metal stamping[J].Procedia Engineering, 2017, 207: 72–77.DOI:10.1016/j.proeng.2017.10.741 |
| [10] | SUQUET P. Elements of homogenization theory for inelastic solid mechanics[C]//Homogenization Techniques for Composite Media. Berlin: Springer, 1987: 193-278. |
| [11] | SMIT R J M, BREKELMANS W A M, MEIJER H E H. Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling[J].Computer Methods in Applied Mechanics & Engineering, 1998, 155(1-2): 181–192. |
| [12] | WHITCOMB J D, CHAPMAN C D, TANG X. Derivation of boundary conditions for micromechanics analyses of plain and satin weave composites[J].Journal of Composite Materials, 2000, 34(9): 724–747.DOI:10.1177/002199830003400901 |
| [13] | XIA Z, ZHANG Y, ELLYIN F. A unified periodical boundary conditions for representative volume elements of composites and applications[J].International Journal of Solids & Structures, 2003, 40(8): 1907–1921. |
| [14] | LI S. Boundary conditions for unit cells from periodic microstructures and their implications[J].Composites Science & Technology, 2008, 68(9): 1962–1974. |
| [15] | 张超, 许希武, 严雪. 纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现[J].航空学报, 2013, 34(7): 1636–1645. ZHANG C, XU X W, YAN X. General periodic boundary conditions and their application to micromechanical finite element analysis of textile composites[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1636–1645.(in Chinese) |
| [16] | SANKAR B V, MARREY R V. A unit-cell model of textile composite beams for predicting stiffness properties[J].Composites Science & Technology, 1993, 49(1): 61–69. |
| [17] | RAVISHANKAR B, SANKAR B V, HAFTKA R T. Homogenization of integrated thermal protection system with rigid insulation bars[C]//Proceeding of the 51st AIAA/ASME/ASCE/AHS/ASC Structure, Structural Dynamics, and Materials Conference. Reston: AIAA, 2010: 2687. |
| [18] | MARTINEZ O M. Micromechanical analysis and design of an integrated thermal protection system for future space vehicles[D]. Gainesville: University of Florida, 2007: 33-55. |
| [19] | SHARMA A, SANKAR B V, HAFTKA R T. Homogenization of plates with microsctructure and application to corrugated core sandwich panels[C]//Proceeding of the 51st AIAA/ASME/ASCE/AHS/ASC Structure, Structural Dynamics, and Materials Conference. Reston: AIAA, 2010: 2706. |
| [20] | 沈观林, 胡更开. 复合材料力学[M].北京: 清华大学出版社, 2013: 80-111. SHEN G L, HU G K. Mechanics of composite materials[M].Beijing: Tsinghua University Press, 2013: 80-111.(in Chinese) |
| [21] | WHITNEY J M. Structural analysis of laminated anisotropic plates[M].Lancaster: Technomic, 1987: 263-312. |
| [22] | HARTLEY P, PILLINGER I. Developments in computational modelling techniques for industrial metal forming processes[J].Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2001, 215(7): 903–914.DOI:10.1243/0954405011518818 |
| [23] | 中华人民共和国国家质量监督检验检疫总局. 金属材料拉伸实验. 第一部分: 室温试验方法: GB/T 228. 1-2010[S]. 北京: 中华人民共和国国家质量监督检验检疫总局, 2010. Standardization Administration of the People's Republic of China. Metallic materials-tensile testing. Part 1: Method of test at room tempertures: GB/T 228. 1-2010[S]. Beijing: Administration of Quality Supervision, Inspection and Quarantine, 2010(in Chinese). |
| [24] | JAVID F, SMITHROBERGE E, INNES M C, et al. Dimpled elastic sheets:A new class of non-porous negative Poisson's ratio materials[J].Scientific Reports, 2015, 5: 18373. |
