国内外对于冲突探测的研究主要分为确定型(也称几何型)和概率型(也称解析型)2类。确定型冲突探测[2-4]一般采用计算几何的方法,判断2架航空器在相遇几何内是否存在潜在飞行冲突。但是实际情况下存在风、导航定位、飞行员操作等不确定性因素引起的误差,将直接影响到冲突探测的准确度。概率型冲突探测[5-7]则通过计算航空器之间的冲突概率,以解析的方法确定是否存在潜在飞行冲突,但是阈值的选取十分关键:如果阈值选取过大,可能造成漏警;如果阈值选取过小,则可能造成大量的误警[8]。
传统的空中交通警戒与防撞系统(Traffic Alert and Collision Avoidance System, TCAS)是当前广泛应用的机载避撞系统[9],主要为飞行员提供空-空碰撞告警。TCASⅠ只提供碰撞告警服务,TCASⅡ除了告警外,还提供冲突解脱建议,但只是简单的爬升和下降机动,此外TCASⅡ在1 000 m以下低空存在较高的虚警率,在通用航空上应用并不广泛[10]。广播式自动相关监视(Automatic Dependent Surveillance-Broadcast,ADS-B)设备结构简单,成本较低,信息更新速率快,监视精度较高,已经广泛用于高空航线飞机和低空通航飞机上[11]。
Lin[12]根据TCAS检测逻辑,设计了一种基于ADS-B和目视飞行规则的针对低空通航小飞机的空域冲突探测和解脱方法。焦玉亮等[13]采用支持向量机(Support Vector Machine, SVM),提出一种针对高空航路的水平二维冲突探测方法。
考虑到通用航空一般在特定空域内飞行,在相对固定的飞行环境中,可以获取丰富的历史飞行数据,通过提前分析这些先验数据,挖掘数据关联特征,提取飞行冲突探测的判定依据,是一种解决低空复杂飞行冲突探测问题的新思路。航空器可以在起飞前加载经过训练的分类器,减少飞行中在线解算的时间,有效解决传统冲突探测算法难以兼顾适用性与解算效率的缺陷。
1 基于SVM的冲突探测 假设空域内的飞机均装有ADS-B OUT设备,飞机获取到由监视空域内其他飞机播发的ADS-B报文数据,由自身的机载设备获取到本机的相关信息。数据选取主要选择目标飞机的识别号(ID)、目标飞机和本机的位置信息和速度信息。目标飞机的位置表示为Pia=(xi, yi, zi),速度为Via(vxi, vyi, vzi),本机的位置表示为Po=(xo, yo, zo),速度为Vo=(vxo, vyo, vzo)。
检测系统的结构如图 1所示。
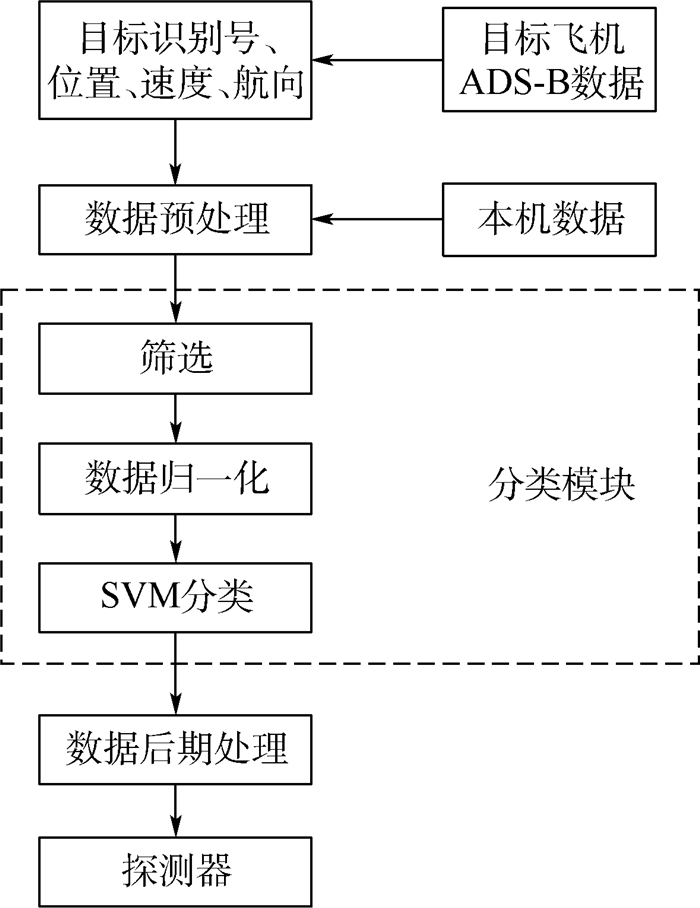 |
| 图 1 检测系统结构 Fig. 1 Detection system structure |
| 图选项 |
1.1 数据预处理 数据预处理主要计算目标飞机相对于本机的位置、速度和航向等信息。
首先以本机为参考,进行坐标转换,得到相对位置PR=(xR, yR, zR)=Pia-Po=(xi-xo, yi-yo, zi-zo),此时,本机位于坐标原点,本机航向方向为Y轴正方向方向。相对速度表示为VR=(vRx, vRy, vRz)=Via-Vo=(vxi-vxo, vyi-vyo, vzi-vzo)。之后,根据相对位置坐标和相对数据坐标计算目标飞机的相对水平航向和垂直航向。根据冲突模型,为避免飞机与飞机发生物理接触,设置一个环绕于飞机的圆柱形区域,该区域同时考虑了冲突模型中2架飞机导航设备的精度而产生的不确定性和飞机本身的尺寸。当一架飞机的位置处于另一架飞机的冲突保护区内时,则认为两架飞机发生冲突。当一架飞机的航迹将在一定时间后到达另一架飞机的冲突保护区内,则认为存在潜在冲突。
为了简化模型,保护区设置为半径528 ft(1 ft=0.304 8 m)的球形,如图 2所示。
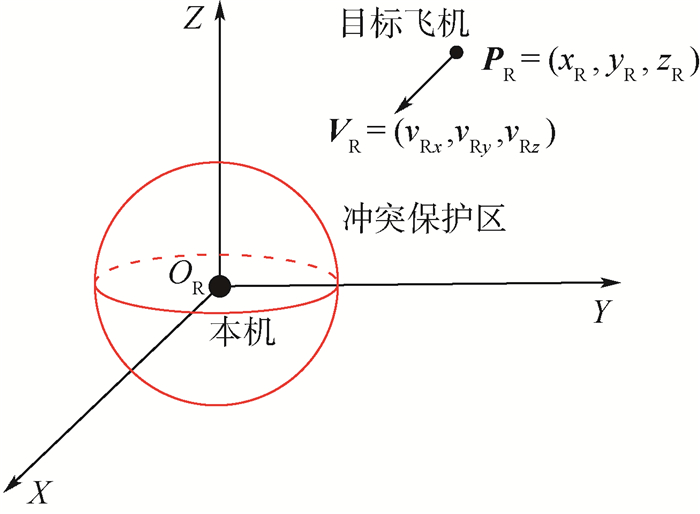 |
| 图 2 保护区模型 Fig. 2 Protection zone model |
| 图选项 |
相对水平航向是以相对坐标系的X轴正方向为基准的。
1) 如果目标飞机的相对速度vRx>0, vRy>0, 水平相对航向为
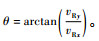
2) 如果目标飞机的相对速度vRx<0, vRy>0或者vRx<0, vRy<0, 水平相对航向为
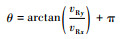
3) 如果目标飞机的相对速度vRx>0, vRy<0, 水平相对航向为
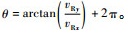
垂直航向是以相对坐标轴中Z轴正方向为基准。
1) 如果垂直相对速度vRz>0,垂直航向为φ=

2) 如果垂直相对速度vRz<0,垂直航向为φ=

将经过预处理的数据Ti=(xRi, yRi, zRi, ‖VRi‖, θRi, φRi)输入SVM模块进行分类判别,xRi、yRi、zRi、θRi、φRi分别为相对经度、相对纬度、相对高度、相对水平航向、相对垂直航向,‖VRi‖=
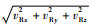
1.2 SVM模块 在将经过预处理的数据输入SVM模块后,笔者首先将数据进行过滤处理,将一些一定不会发生冲突的目标提前进行分类处理,如表 1所示。
表 1 无冲突判定准则 Table 1 No conflict judgment criteria
| 卦限编号 | 卦限区间 | 无冲突判定准则 |
| 1 | xR>0, yR>0, zR>0 |  |
| 2 | xR<0, yR>0, zR>0 | 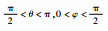 |
| 3 | xR<0, yR<0, zR>0 | 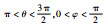 |
| 4 | xR>0, yR<0, zR>0 | 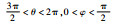 |
| 5 | xR>0, yR>0, zR<0 | 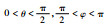 |
| 6 | xR<0, yR>0, zR<0 | 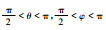 |
| 7 | xR<0, yR<0, zR<0 | 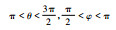 |
| 8 | xR>0, yR<0, zR<0 | 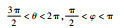 |
表选项
经过训练的SVM分类器对经过过滤和归一化的输入数据进行分类。对于所有的分类目标,如果在t时刻目标为存在潜在冲突可能,则在假设对于第i架飞机在t时刻的预测值为Pt(Ti)=1,如果目标在t时刻经过SVM分类检测不存在冲突可能,则Pt(Ti)=-1。
数据后期处理主要采用移动平均加权,考虑到对飞机的冲突检测是一个连续的过程,在某个时间点对冲突进行探测,需要考虑前一段时间的预测结果。移动加权平均的滑动窗口为m,滑动加权系数w={wt-m+1, …, wt-1, wt},则对于第i架飞机在t时刻经过移动加权平均后的预测值为
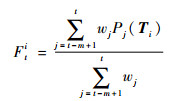 |
设置判断阀值T(固定常量)。如果Fti>T, 则在t时刻对于此目标飞机判定为存在冲突的可能,否则判为非冲突目标。
2 支持向量机 SVM是由Cortes和Vapnik[14]提出的一种基于统计学习理论的机器学习方法,它是基于结构风险最小化原则对数据进行分类,将原始数据通过核函数映射到高维空间中,采用线性超平面对数据进行分类,解决了在低维数据空间中线性不可分的问题。常用的核函数有:线性核函数为〈α·αi〉;多项式核函数为(〈α·αi〉+R)d;径向基核函数为
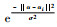
通过选取适当的核函数及相应的参数,以及惩罚因子C, 可以建立一个适当的分类模型对数据进行分类。所以,参数的选取是建立SVM模型的重要步骤。本文选取径向基函数作为其核函数,涉及到的参数有C和σ。
C主要影响建立SVM模型的复杂度。较高的C使得模型的复杂度高,但模型的推广能力差,C越低,建立的模型越简单,模型的推广能力越高。较高的C虽然使得模型训练准确度高,但是对于预测样本的分类正确率低。
σ控制了径向的作用范围,σ越高,对于特征数据的映射能力越弱,σ越低,映射能力越强,但是可能会造成过拟合的情况。
传统的参数选取的方法包括网格搜索(Grid-Search)法和经验选择法,经验选择法虽然简单,但是存在很大的主观性。网格搜索法在一定的搜索空间中以一定的步进逐步搜索,但是存在计算量大,搜索精度不足等问题。
近年来,国内外许多研究****采用进化算法对SVM的参数进行选取。常用的有遗传(GA)算法和粒子群(PSO)算法。GA算法借鉴生物界中生物进化繁衍的规律,通过对个体的选择、交叉、变异等操作来寻找解空间的潜在最优解。但是GA算法具有较大的随机性,且算法本身的参数设置过多,容易产生早熟收敛等问题。PSO算法模拟鸟群捕食行为,通过考虑粒子的个体最优值和全体最优值来引导粒子的搜索策略。但是PSO算法同样存在容易陷入局部最优的情况,切对于粒子的初始值比较敏感。所以本文结合GA和PSO算法各自的优点,提出一种GA-PSO混合算法,来解决SVM的参数寻优问题,训练流程如图 3所示。
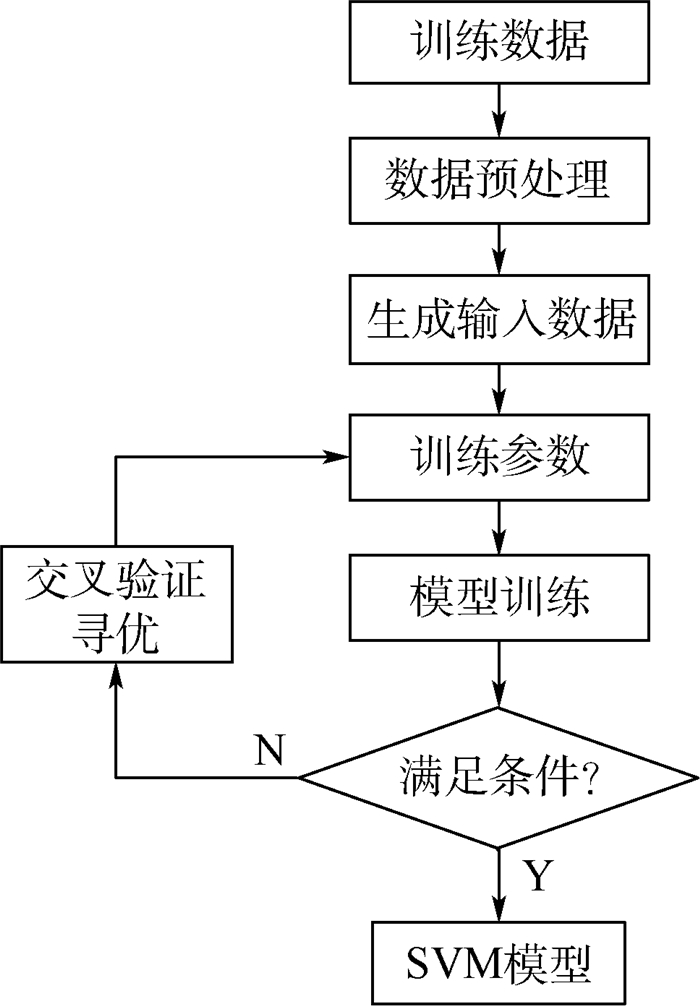 |
| 图 3 GA-PSO混合算法训练流程 Fig. 3 GA-PSO hybrid algorithm training process |
| 图选项 |
2.1 GA-PSO混合算法 PSO算法粒子种群由n个粒子组成X=(X1, X2, …, Xn),每一个粒子位置Xi=(xi1, xi2, …, xiD),D为解空间的维数;每一个粒子的速度为Vi=(Vi1, Vi2, …, ViD),以K类交叉验证(cross-validation)[15]正确率作为粒子的适应度函数P。所谓K类交叉验证,就是将训练集平均分为K份,每次取1份作为测试集,剩余的K-1份作为训练集,然后采用当前的参数取值,也就是粒子位置Xi=(xi1, xi2, …, xiD)作为训练参数时进行模型的建立和对测试集的分类,最后将K个模型的分类正确率平均。个体极值为Pi=(Pi1, Pi2, …, PiD),全局极值为Pg=(Pg1, Pg2, …, PgD),粒子的更新公式为
 |
式中:k为种群的当前迭代次数;c1、c2为加速度常数;r1、r2为(0, 1)之内的随机数。
粒子的位置变化幅度是由粒子的飞行速度的大小决定的,粒子飞行速度大,能够在短时间内飞到搜索空间中最优解的区域,其全局搜索能力较强,粒子飞行速度较低时,粒子的位置变化幅度较小,有利于增加搜索的精度,局部搜索能力强,全局搜索能力弱。但是,如果粒子的飞行速度一直保持一个较高的值,可能会导致粒子越过最优解区域,飞行速度一直较低的时候,虽然搜索的精度会增加,但是可能导致粒子陷入局部最优解。所以对速度更新公式增加了一个加权系数:
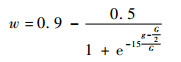 |
式中:g为当前迭代次数;G为最大迭代次数。以此,粒子在迭代初期能够保持较高的更新速度,以获得较强的全局搜索能力,在迭代后期具有较低的更新速度,具有较强的局部搜索能力,w变化曲线如图 4所示。
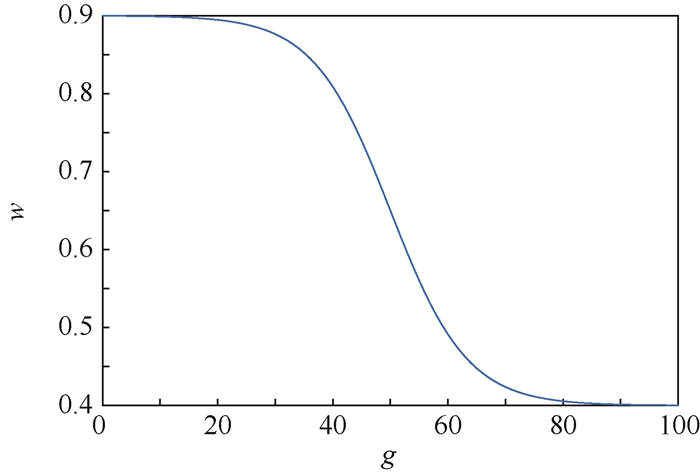 |
| 图 4 w变化曲线 Fig. 4 Variation curve of w |
| 图选项 |
在算法迭代初期,为了加大粒子的不确定度,增强算法的全局搜索能力参考遗传算法的机理,对粒子进行变异,具体流程如图 5所示。
 |
| 图 5 粒子变异流程 Fig. 5 Particle variation process |
| 图选项 |
步骤1??设定种群规模和迭代次数, 搜索空间大小和速度大小等参数。根据限制随机初始化粒子的位置X=(X1, X2, …, Xn)和速度V=(V1, V2, …, Vn)。
步骤2??根据每个粒子的位置Xi=(xi1, xi2)对模型进行训练,将交叉验证正确率作为该粒子的适应度。
步骤3??根据每个粒子的适应度和其历史位置上的适应度相比较,将适应度较高的作为新的个体极值Pi=(Pi1, Pi2, …, PiD)。
步骤4??根据每个粒子的适应度和所有粒子经过的最优适应度相比较,将适应度较高的作为新的全局极值Pg=(Pg1, Pg2, …, PgD)。
步骤5??根据粒子的速度和位置更新公式对粒子进行更新。
步骤6??迭代次数是否满足条件g<40,若满足进行步骤7,是否满足最大迭代次数,如果满足,输出结果,若不满足,返回步骤3。
步骤7??计算粒子的适应度值,根据粒子适应度的大小按一定比例选从种群Z取出种群Z2。
步骤8??对Z2进行重组交叉。
步骤9??对Z2进行变异。
步骤10??计算Z2的适应度,根据适应度重插入种群Z中,保留适应度高的,排除适应度低的。
步骤11??返回步骤3。
2.2 算法比较 实验的相关参数设置如表 2所示。
表 2 3种算法参数 Table 2 Parameters of three algorithms
| 参数 | GA算法 | PSO算法 | GA-PSO混合算法 |
| 训练代数 | 100 | 100 | 100 |
| 种群大小 | 30 | 30 | 30 |
| c1 | N/A | 1.5 | 1.5 |
| c2 | N/A | 1.7 | 1.7 |
| 代沟 | 0.9 | N/A | 0.5 |
| 交叉概率 | 0.7 | N/A | 0.7 |
| 变异概率 | 0.02 | N/A | 0.02 |
| 注:N/A表示不适用。 | |||
表选项
采用5-折交叉验证,分别生成了3组训练数据,比较GA、PSO和GA-PSO 3种算法的寻优性能。训练数据为经过过滤和归一化的目标飞机状态信息,包含目标飞机的相对位置、相对速度和相对航向角等信息,如表 3所示。
表 3 归一化飞行状态 Table 3 Normalized flight status
| 飞机序号 | 相对经度xRi | 相对纬度yRi | 相对高度zRi | 相对速度‖VRi‖ | 相对航向角θRi |
| 1 | 0.34 | 0 | 0.212 | -1 | 0.2 |
| 2 | 0.78 | -0.5 | -0.261 | 0.2 | 0.5 |
| 3 | -0.88 | 1 | 0.921 | 0 | 0.1 |
| | | | | | |
| N | -0.44 | 0.34 | 0 | -0.3 | 0.8 |
| 注:xRi、yRi、zRi、‖VRi‖的区间为[-1, 1];θRi区间为[0, 1]。 | |||||
表选项
记录训练过程中的每一代的交叉验证正确率,针对每组数据,采用3种算法分别进行50次寻优,记录训练过程中每一代的平均正确率。图 6为训练数据样本为200个的时候,训练过程中,交叉验证过程适应度的变化。
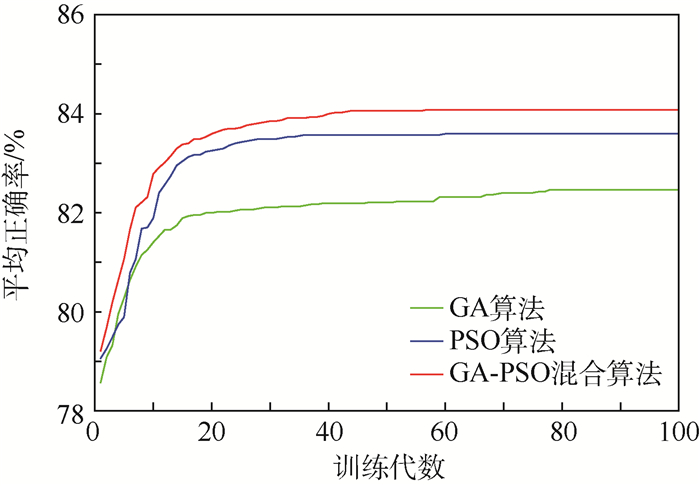 |
| 图 6 交叉验证平均正确率 Fig. 6 Average accuracy of cross-validation |
| 图选项 |
将50次的训练结果作为参数去分别训练SVM模型,并对测试数据进行预测分类,测试数据为目标飞机相对状态信息,其中一半为冲突状态,另一半为非冲突状态。
平均正确率统计如表 4所示。
表 4 SVM模型的平均正确率 Table 4 Average accuracy of SVM models
| % | |||
| 训练集(冲突-非冲突) | GA算法 | PSO算法 | GA-PSO混合算法 |
| 100-100 | 82.016 9 | 81.903 | 82.789 |
| 150-150 | 87.649 8 | 87.603 4 | 89.029 |
| 200-200 | 82.713 1 | 83.641 4 | 84.244 |
| 300-300 | 85.779 7 | 87.139 8 | 87.411 |
表选项
可以看出,GA-PSO混合算法能够克服原GA和PSO算法过早收敛的不足。由于寻优前期较大的随机性和随着训练代数而变化的粒子速度。由于GA-PSO混合算法具有较好的全局寻优能力,在局部寻优时也有较好的准确性,其能够搜索到更优的解。
3 仿真分析 以经典的CESSNA 172单引擎飞机作为目标参考(其主要参数见表 5),生成了4 000个作为训练数据,其中包含2 000个冲突飞机的特征数据,2 000个不冲突飞机的特征数据,相对位置坐标位于本机水平范围0.9~3.0 nmi(1 nmi=1.852 km)。选取RBF径向基核函数,采用GA-PSO混合算法寻得训练参数。
表 5 CESSNA 172的尺寸和性能 Table 5 Dimensions and performance of CESSNA 172
| 尺寸 | 数值 | 主要性能 | 数值 | |
| 长/ft | 27.2 | 最大巡航速度/(km·h-1) | 230 | |
| 高/ft | 8.9 | 最大航程/nmi | 640(1 185 km) | |
| 翼展/ft | 36.1 | 最大爬升率/(ft·mim-1) | 730(223 m/min) | |
| 极限速度/(km·h-1) | 302 | |||
| 失速速度/(km·h-1) | 89 | |||
| 注:最大承载人数为4。 | ||||
表选项
采用蒙特卡罗方法对该方法的性能进行分析,生成测试数据一共20组,每组一共包含500个航迹信息,250个冲突航迹和250个不冲突的航迹,航迹的初始相对位置位于本机监视范围1.3~3.0 nm之间,针对每个航迹,进行持续10 s的检测时间,监视范围为水平1~3 nm,如果目标飞机位置处于在水平监视范围以外时停止检测,垂直检测范围为1 000 m以下,测试统计结果如表 6所示。
表 6 用于检测的统计数据 Table 6 Statistical data for detection
| 检测总次数 | 冲突航迹检测次数 | 不冲突航迹检测次数 |
| 104 069 | 51 680 | 52 439 |
表选项
表 7显示了所提出的检测系统的性能。初始检测状态是指第1 s时,SVM对目标飞机状态的分类结果,-1为非冲突,1为冲突。10 s内检测是指对目标的航迹进行持续10 s的检测,不经过移动平均加权时,-1为非冲突,1为冲突,经过移动平均时,Fti≥T为冲突,Fti<T为不冲突,此处,移动步数为3,加权系数w={2, 3, 5},T=0。
表 7 检测系统性能的统计数据 Table 7 Statistical data for performance of detection system
| 性能 | 初始检测状态 | 10 s内检测 | |
| 不经过移动加权平均 | 经过移动加权平均 | ||
| 漏警数 | 10 | 57 | 52 |
| 误警数 | 363 | 3 280 | 3 277 |
| 漏警率/% | N/A | 0.110 3 | 0.100 6 |
| 误警率/% | N/A | 6.254 9 | 6.249 2 |
表选项
4 结论 1) 本文提出的基于SVM的冲突探测算法,将冲突探测问题转化为一个规划求解的问题。首先对ADS-B报文数据进行筛选和归一化处理,其次通过GA-PSO混合算法完成SVM的参数选优,并通过先验信息对SVM进行训练,最后通过移动加权平均,优化SVM分类判定结果,实现了基于SVM的飞行冲突探测。
2) 通过对比参数优化及探测能力实验结果,GA-PSO混合算法在参数优化上性能优良,确保训练后的SVM在冲突探测时保持了较高的正确率和解算速度,本文算法适用于解决低空复杂飞行冲突探测问题。
参考文献
| [1] | GARIEL M, HANSMAN R, FRAZZOLI E. Impact of GPS and ADS-B reported accuracy on conflict detection performance in dense traffic: AIAA-2011-6893[R]. Reston: AIAA, 2011. |
| [2] | FULTON N L. Airspace design:Towards a rigorous specification of complexity based on computational geometry[J].Aeronautical Journal, 1999, 103(1020): 75–84.DOI:10.1017/S0001924000027779 |
| [3] | CHIANG, YI J, KLOSOWSKI J, et al. Geometric algorithms for conflict detection and resolution in air traffic management[C]//36th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 1997, 2(2): 1835-1840. |
| [4] | MCDONALD J, VIVONA R. Strategic airborne conflict detection of air traffic and area hazards: NAS2-98005[R]. Washington, D. C. : NASA, 2000. |
| [5] | PRANDINI M, HU J, SASTRY S. A probabilistic approach to aircraft conflict detection[J].IEEE Transactions on Intelligent Transportation Systems, 2000, 1(4): 199–220.DOI:10.1109/6979.898224 |
| [6] | JARDIN M R. Grid-based strategic air traffic conflict detection: AIAA-2005-5826[R]. Reston: AIAA, 2005. |
| [7] | HU J. Aircraft conflict detection in presence of spatially correlated wind perturbations: AIAA-2003-5339[R]. Reston: AIAA, 2003. |
| [8] | 李彬, 吴珍珍. 基于航迹预测的飞行冲突预测[J].微处理机, 2011(2): 73–80. LI B, WU Z Z. Flight conflict detection based on flight path prediction[J].Microprocessors, 2011(2): 73–80.(in Chinese) |
| [9] | 韩艳茹, 敬忠良, 龚嘉琦. 空中交通预警与防撞系统(TCAS)风险及对策研究[J].计算机测量与控制, 2012, 20(3): 737–740. HAN Y R, JING Z L, GONG J Q. Research of traffic alert and collision avoidance system(TCAS) risk and countermeasure[J].Computer Measurement & Control, 2012, 20(3): 737–740.(in Chinese) |
| [10] | WILLIAMSON T, SPENCER N A. Development and operation of the traffic alert and collision avoidance system(TCAS)[J].Proceedings of the IEEE, 1989, 77(11): 1735–1744.DOI:10.1109/5.47735 |
| [11] | 林熙. 密集飞行条件下的间隔自主保持方法研究[D]. 北京: 北京航空航天大学, 2011: 11-13. LIN X. Research on self-separation assurance methods in condition of intensive flight[D]. Beijing: Beihang University, 2011: 11-13(in Chinese). |
| [12] | LIN C E. Collision avoidance solution for low-altitude flights[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2011, 225(7): 779–790.DOI:10.1177/0954410011399211 |
| [13] | JIAO Y L, ZHANG X J, GUAN X M. An algorithm for airborne conflict detection based on support vector machine[J].Applied Mechanics and Materials, 2012, 229-231: 1140–1145.DOI:10.4028/www.scientific.net/AMM.229-231 |
| [14] | CORTES C, VAPNIK V. Support-vector networks[J].Machine Learning, 1995, 20(3): 273–276. |
| [15] | KOHAVI R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence. New York: ACM, 1995: 1137-1143. |
