基于上述背景,本文就转运策略在三站点库存组织中对系统期望延期交货量(EBO)的影响展开研究。文献[22]制定了按固定概率进行备件供应保障的转运策略(站点的备件需求根据固定概率由指定站点提供备件保障),并对采用此策略的三站点库存系统进行了建模和分析。本文在此基础上,对备件转运策略进行拓展和延伸,制定了具有优先级约束的备件转运策略(在选择备件供应保障站点时具有偏好),并针对三站点库存系统建立了新的库存转运模型。通过2种转运策略对库存系统EBO的影响分析可以发现不同备件转运策略的可行作用空间。上述发现可以为多站点库存系统备件的供应与补给提供指导性意见。
1 问题描述和建模 1.1 问题描述 保障站点由于库存量的约束或维修能力的限制,存在由其他站点进行紧急供货以及将部分故障件送去其他站点维修的情况。文献[22]中按照固定概率规定了备件转运策略,但当目标站点无可用库存时,进行目标站点的更换往往会带来更积极的作用。为了方便与文献[22]作对比,本文设定,各站点产生的备件需求部分由本地站点满足,部分由其他站点转运满足,其他站点的选择依需求产生站点的顺时针方向具有优先级,如图 1所示。
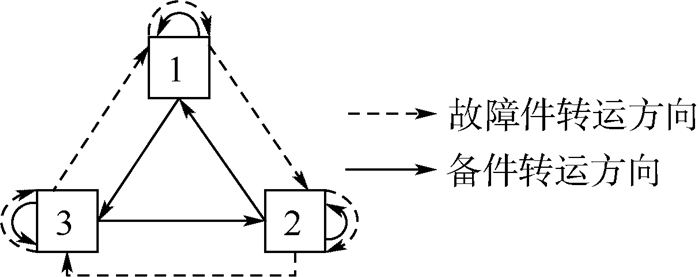 |
| 图 1 部件在三站点库存组织中的转运模型 Fig. 1 Transshipment model of items in three-site inventory system |
| 图选项 |
图 1中各站点的备件需求有rii的概率由本地满足,有1-rii的概率通过其他站点的转运满足。与此同时,提供备件的站点将会接收对应的故障件进行修复,修复后的故障件将被作为备件重新放入备件仓库。依图 1所示规则,当首选站点无可用备件时,便继续寻找下一站点。如果所有备选站点均无可用备件,将强制选择最后的备选站点作为备件供应站点,此时被选站点的备件延期交货将对源站点产生影响。本研究中采用的主要假设如下:
1) 站点自身产生的备件需求服从均值为di(i=1, 2, 3)的泊松分布。
2) 站点维修能力不设限,因此不存在故障件维修延迟现象。
3) 站点内故障件的维修时间相互独立,且服从均值为1/ui(i=1, 2, 3)的指数分布。
4) 故障件经送修后修复如新。
5) 各站点库存盘点策略为(s-1, s), s为初始库存量。
1.2 模型建立 在稳态下,库存状态关系式如下[27]:
 | (1) |
式中:sOH为可用库存;sDI为应得备件数,涵盖了处于修理环节、运输环节以及其他站点对本站点延期交货的备件及故障件;sBO为备件延期交货量。
令sMi为正在站点i处维修的故障件数;sTPji和sTFji分别为站点j运往站点i途中的备件数和故障件数;sBOji为站点j对站点i的延期交货量。定义站点i顺时针方向的第1个站点为j,第2个站点为k,那么站点i的应得备件数sDIi可以表示为
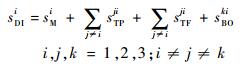 | (2) |
式(2)各部分的表达式分别为
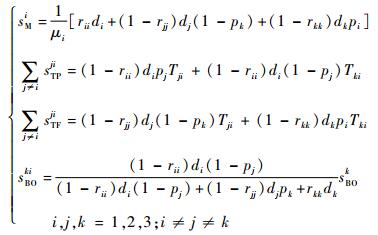 | (3) |
式中:Tij为站点i到站点j的运输时间;μi为站点i的故障件平均维修速率; pi为站点i处的备件满足率,其定义为
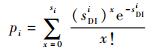 | (4) |
其中:si为站点i的初始库存量。
sBOi为站点i的延期交货量,稳态下可以表示为延期交货量期望值的形式:
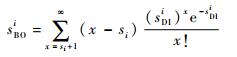 | (5) |
2 方程分析及求解 2.1 方程分析 将式(3)代入式(2)得到
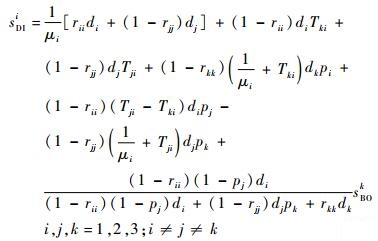 | (6) |
对式(6)进行简化,记:
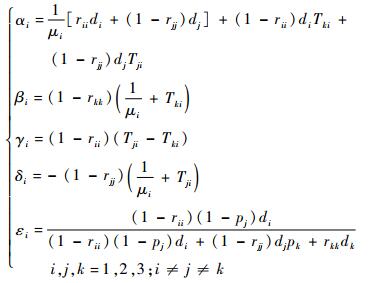 | (7) |
同时令sBOi=θisDIi,其中θi为sBOi与sDIi之间的比例系数,因为0 < sBO≤sDI,所以0 < θi≤1。可分别得到sDI1、sDI2、sDI3的表达式,整理成式(8)。
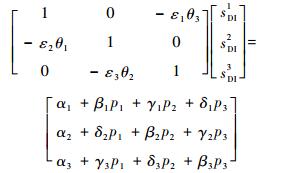 | (8) |
定义

如果|A|>0,那么A-1存在,方程式(8)有唯一解。
如果|A|=0,即ε1ε2ε3θ1θ2θ3=1,此时必有ε1ε2ε3=1及θ1θ2θ3=1。根据式(6)可得
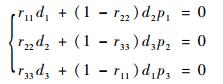 | (9) |
因为pi>0,所以式(8)无解,因此|A|=0的情况不存在。综上所述,模型具有唯一解。
2.2 求解算法设计 令sDI=[sDI1, sDI2, sDI3]T,fn(sDI)(n=1, 2, 3)表示式(8)等号右侧矩阵中每一项与sDI之间的函数关系,那么方程式(8)可以写成
 | (10) |
根据2.1节分析可知方程的映射关系为压缩映射,参考式(10),可以采用迭代法构造柯西列逼近方程解,过程参见图 2。图 2中m为迭代次数,ε为误差精度,sDI(m)为m轮迭代的输入值,sDI(m)*为m轮迭代的输出值,通过对比输入输出的差值与ε的大小确定迭代是否终止。
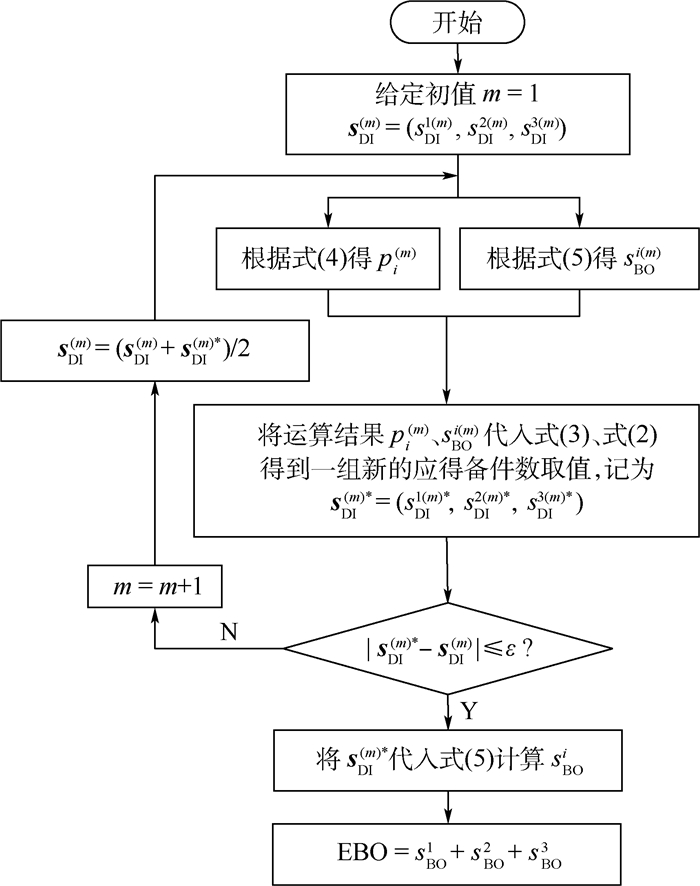 |
| 图 2 算法流程图 Fig. 2 Algorithm flowchart |
| 图选项 |
3 不同转运策略算例 记文献[22]中转运策略对应模型Ⅰ,本文转运策略对应模型Ⅱ。将表 1中的数据作为基础输入,利用MATLAB软件展开参数影响分析。
表 1 基础数据 Table 1 Basic data
| 参数 | si/个 | di/(个·h-1) | ui/(个·h-1) | rii | Tij/h | Tik/h |
| 数值 | 15 | 0.12 | 0.05 | 0.2 | 50 | 50 |
| ??注:文献[22]中模型Ⅰ还包含2个输入参数rij和rik,分别代表了站点i的备件需求中由站点j、k提供备件满足的概率,案例中规定rij=rik=(1-rii)/2。 | ||||||
表选项
3.1 库存配置方案对模型输出的影响 令s1+s2+s3=50,首先取s1=0,s2从0取值,逐次增加5,直到等于(50-s1)停止。然后s1逐次增加5,从而产生共66组(s1, s2, s3)库存配置方案并按其产生顺序进行编号,记库存方案编号为N,则N=1, 2, …, 66。将每种库存方案代入模型进行计算,得到模型Ⅰ的系统期望延期交货量EBO1和模型Ⅱ的系统期望延期交货量EBO2,结果反映在图 3。
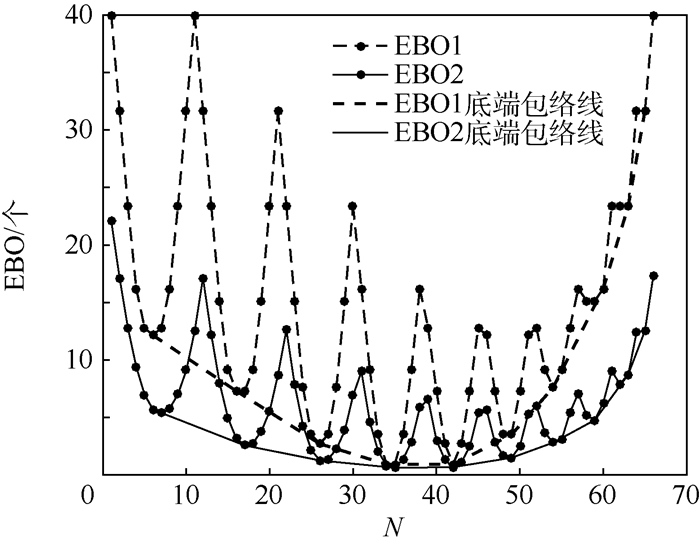 |
| 图 3 库存配置方案(s1+s2+s3=50)对系统EBO的影响曲线 Fig. 3 Influence curves of inventory allocation schemes (s1+s2+s3=50) on system EBO |
| 图选项 |
图 3中2条底端包络曲线的最低点为最优库存配置方案,此时站点库存配置量与站点实际需求相对应。同时图中有EBO1≥EBO2,因为本文转运策略相对模型I的优势在于考虑到站点实时库存状况,提高备件利用率,能够降低系统EBO。但在不同的配置方案下,EBO1-EBO2的值会有所变化。
局部放大图 3中方案编号1~11输出曲线,得到图 4。从图 4中可以看出两模型最优库存配置不一致。对于模型Ⅰ,需求分配根据概率进行,各站点实际需求完全相等,所以站点1库存为零的情况下,站点2、3库存相等为最优配置。而对于模型Ⅱ,站点1备件满足率接近0,站点2、3备件满足率接近1,那么站点2、3的实际需求分别近似等于
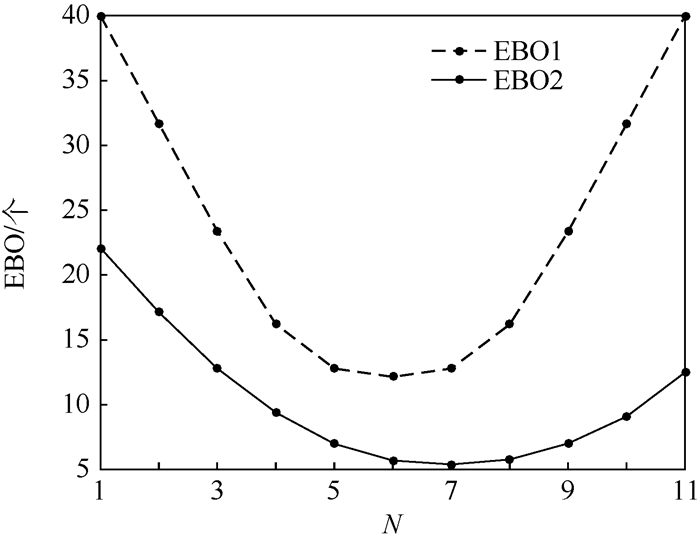 |
| 图 4 库存配置方案(s1=0, s2+s3=50)对系统EBO的影响曲线 Fig. 4 Influence curves of inventory allocation schemes (s1=0, s2+s3=50) on system EBO |
| 图选项 |
 | (11) |
所以站点2初始库存稍大于站点3的情况为最优库存配置。由此说明,模型Ⅱ中各站点的实际需求与站点库存量相关,导致其最优库存配置与模型Ⅰ不一致。
3.2 备件需求由本地满足的概率对模型输出的影响 根据图 5,随着备件需求由本地满足的概率rii(i=1, 2, 3)上升,站点间由转运满足的备件需求下降,那么转运策略的作用域缩小,2种策略之间的优劣对比就更不明显。因此,需求由本地满足的概率决定了转运策略的作用空间大小。当其等于1时,转运策略不发挥作用。
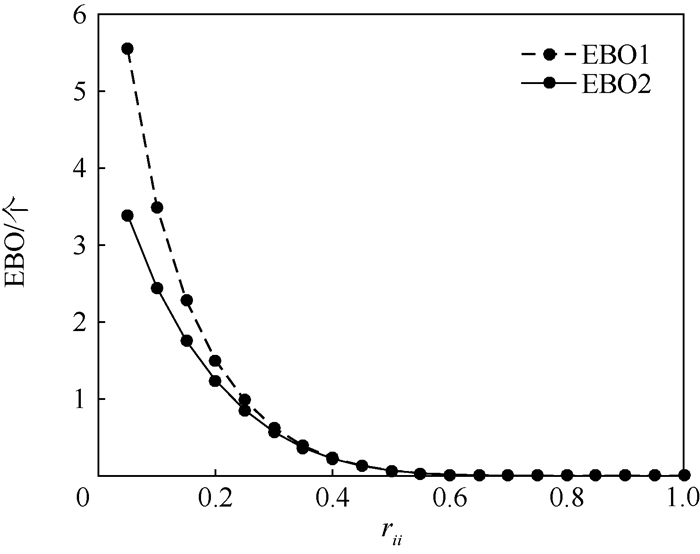 |
| 图 5 备件需求由本地满足的概率对系统EBO的影响曲线 Fig. 5 Influence curves of probability of demands filled by local site on system EBO |
| 图选项 |
在图 5中,随rii增大,系统EBO下降。因为本案例中,各站点为最优库存配置,各站点相互独立自给自足时效能最高,此时rii=1。rii不等于1时,不必要的转运造成系统EBO增大,且rii越小,转运带来的消极影响越大。从而说明了站点库存配置与站点需求不对应时,备件转运才会产生积极影响,否则额外的转运会降低系统效能。
3.3 站点需求率、维修速率和站点间运输时间对模型输出的影响 缺货意味着可用备件满足不了备件需求,而可用备件包括了库存和过程中修复如新的故障件。为了排除库存的影响,这里设置si=0(i=1, 2, 3)。
根据图 6及式(3)进行分析:站点需求率di与维修速率ui共同作用影响系统EBO。站点需求率与维修速率的比值di/ui较小时,故障件转化成备件的速度近似满足备件需求,此时对于系统中的有限备件而言,模型Ⅱ的转运策略能够提高备件利用率,因此EBO1>EBO2;当di/ui较大时,维修产生的备件数量相对需求量过于少,系统EBO增大。此时提高备件共享率所带来的积极效果很微弱,因此EBO2曲线与EBO1曲线逐渐重合,但是2条曲线重合点的位置与其他模型参数相关。
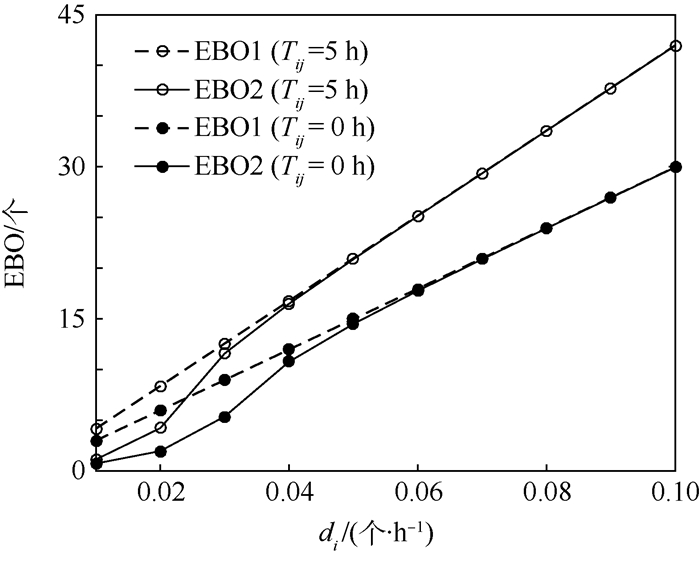 |
| 图 6 需求率和运输时间对系统EBO的影响曲线 Fig. 6 Influence curves of demanding rate and transport time on system EBO |
| 图选项 |
由此可以总结出需求率和维修速率的相对大小,对于模型输出和运输策略作用的发挥具有显著影响。且可用库存降为0之后,系统维修速率与需求率的相互作用才开始起主导作用。在此之前,配置库存的共享为主导过程。
同时从图 6可以看出, EBO受运输时间Tij的影响并随时间的增大而增大。因为运输时间增加会延长故障件处于维修周转状态的时间和可用备件的送达时间,因此对需求得到满足的数量和时间产生消极影响。
4 结论 1) 具有优先级约束的转运策略能够提高备件利用率并降低系统EBO,但是作用效果主要由转运策略的可行作用空间大小决定。作用空间的可行变化范围主要由备件需求由本地满足的概率、库存配置方案以及需求率与维修速率决定。其中,备件需求由本地满足的概率决定了转运策略的作用域;可用库存不为零时配置方案的合理性决定了转运策略的作用效果,而可用库存降为零后维修速率与需求率的相对大小决定转运策略的作用效果。
2) 据此如果所有备件需求统一处理,优先选择本地备件保障,在本地无可用库存时依据优先级条件选择其他站点,并在所有站点无可用库存时,将故障件留在本地进行维修同时等待本地提供备件保障,系统的备件利用率将进一步提高,这一点在后续研究将进行论证。另外,本文的转运策略本质上是用运输成本增加来换取缺货成本降低,缺少经济性权衡分析,这可以作为以后的研究方向。
参考文献
| [1] | SHERBROOKE C C. METRIC:A multi-echelon technique for recoverable item control[J].Operations Research, 1968, 16(1): 122–141.DOI:10.1287/opre.16.1.122 |
| [2] | MUCKSTADT J A. A model for a multi-item, multi-echelon, multi-indenture inventory system[J].Management Science, 1973, 20(4): 472–481. |
| [3] | SLAY F M. VARI-METRIC: An approach to modeling multi-echelon resupply when the demand process is Poisson with a gamma prior: Report AF301-3[R]. Washington, D. C. : Logistics Management Institute, 1984. |
| [4] | SHERBROOKE C C. VARI-METRIC:Improved approximations for multi-indenture, multi-echelon availability models[J].Operations Research, 1986, 34(2): 311–319.DOI:10.1287/opre.34.2.311 |
| [5] | AXSATER S. Modelling emergency lateral transshipments in inventory systems[J].Management Science, 1990, 36(11): 1329–1338.DOI:10.1287/mnsc.36.11.1329 |
| [6] | KRANENBURG A A, HOUTUM G J V. A new partial pooling structure for spare parts networks[J].European Journal of Operational Research, 2009, 199(3): 908–921.DOI:10.1016/j.ejor.2009.01.057 |
| [7] | LEE H L. A multi-echelon inventory model for repairable items with emergency lateral transshipments[J].Management Science, 1987, 33(10): 1302–1316.DOI:10.1287/mnsc.33.10.1302 |
| [8] | TER S. Exact and approximate evaluation of batch-ordering policies for two-level inventory systems[J].Operations Research, 1993, 41(4): 777–785.DOI:10.1287/opre.41.4.777 |
| [9] | 董琪, 徐延学, 丛林虎. 基于Markov三级库存系统备件横向调拨配置模型[J].系统工程与电子技术, 2015, 37(11): 2524–2530. DONG Q, XU Y X, CONG L H. Allocation model of spare parts for three-echelon inventory system with lateral transshipment based on Markov[J].Systems Engineering and Electronics, 2015, 37(11): 2524–2530.(in Chinese) |
| [10] | 张光宇, 李庆民, 郭璇. 基于横向转运策略的可修备件多点库存建模方法[J].系统工程与电子技术, 2012, 34(7): 1424–1429. ZHANG G Y, LI Q M, GUO X. Modeling for repairable spare parts in multi-location inventory system with lateral transshipments[J].Journal of Systems Engineering and Electronics, 2012, 34(7): 1424–1429.(in Chinese) |
| [11] | ALFREDSSON P, VERRIJDT J. Modeling emergency supply flexibility in a two-echelon inventory system[J].Management Science, 1999, 45(10): 1416–1431.DOI:10.1287/mnsc.45.10.1416 |
| [12] | OLSSON F. An inventory model with unidirectional lateral transshipments[J].European Journal of Operational Research, 2010, 200(3): 725–732.DOI:10.1016/j.ejor.2009.01.024 |
| [13] | AXSATER S. Evaluation of unidirectional lateral transshipments and substitutions in inventory systems[J].European Journal of Operational Research, 2003, 149(2): 438–447.DOI:10.1016/S0377-2217(02)00447-2 |
| [14] | 阮旻智, 刘任洋. 基于横向转运策略的多级库存配置建模与优化[J].中国工程科学, 2015, 17(5): 106–112. RUAN M Z, LIU R Y. Modeling and optimization for multi-echelon spares inventory configuration with lateral transshipments[J].Engineering Sciences, 2015, 17(5): 106–112.(in Chinese) |
| [15] | DIKS E B, KOK A G D. Controlling a divergent 2-echelon network with transshipments using the consistent appropriate share rationing policy[J].International Journal of Production Economics, 1996, 45(1-3): 369–379.DOI:10.1016/0925-5273(95)00007-0 |
| [16] | OLSSON F. Optimal policies for inventory systems with lateral transshipments[J].International Journal of Production Economics, 2009, 118(1): 175–184.DOI:10.1016/j.ijpe.2008.08.021 |
| [17] | JUNG B R, SUN B G, KIM J S, et al. Modeling lateral transshipments in multiechelon repairable-item inventory systems with finite repair channels[J].Computers & Operations Research, 2003, 30(9): 1401–1417. |
| [18] | ALVAREZ E M, HEIJDEN M C V D, VLIEGEN I M H, et al. Service differentiation through selective lateral transshipments[J].European Journal of Operational Research, 2013, 237(3): 824–835. |
| [19] | KRANENBURG A A, HOUTUM G J V. A new partial pooling structure for spare parts networks[J].European Journal of Operational Research, 2009, 199(3): 908–921.DOI:10.1016/j.ejor.2009.01.057 |
| [20] | KUKREJA A, SCHMIDT C P, MILLER D M. Stocking decisions for low-usage items in a multilocation inventory system[J].Management Science, 2001, 47(10): 1371–1383.DOI:10.1287/mnsc.47.10.1371.10263 |
| [21] | 包记凯, 罗长远, 周道水, 等. 维修备件横向转运库存优化模型[J].信息工程大学学报, 2014, 15(1): 24–28. BAO J K, LUO C Y, ZHOU D S, et al. Optimization model for maintenance spare parts inventory system with lateral transshipments[J].Journal of Information Engineering University, 2014, 15(1): 24–28.(in Chinese) |
| [22] | 张颖, 王蕴, 薛佩. 三站点备件供应保障关系建模与分析[J].北京航空航天大学学报, 2017, 43(8): 1625–1631. ZHANG Y, WANG Y, XUE P. Modeling and analysis of spares supply support relations among three stations[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(8): 1625–1631.(in Chinese) |
| [23] | NONAS L M, JORNSTEN K. Optimal solutions in the multi-location inventory system with transshipments[J].Journal of Mathematical Modelling and Algorithms in Operations Research, 2007, 6(1): 47–75.DOI:10.1007/s10852-006-9049-y |
| [24] | TAGARAS G. Pooling in multi-location periodic inventory distribution systems[J].Omega, 1999, 27(1): 39–59.DOI:10.1016/S0305-0483(98)00030-9 |
| [25] | 张勇, 杨宏伟, 杨学强, 等. 基于复杂网络理论的装备保障网络模型研究[J].上海理工大学学报, 2012, 34(5): 429–434. ZHANG Y, YANG H W, YANG X Q, et al. Model of equipment support network based on theory of complex networks[J].Journal of University of Shanghai for Science and Technology, 2012, 34(5): 429–434.(in Chinese) |
| [26] | 张勇, 杨宏伟, 白勇, 等. 基于复杂网络理论的装备保障网络实证研究[J].装备学院学报, 2014, 25(1): 83–87. ZHANG Y, YANG H W, BAI Y, et al. An empirical study on the equipment support network based on complex networks[J].Journal of Academy of Equipment, 2014, 25(1): 83–87.(in Chinese) |
| [27] | SHERBROOKE C C. Optimal inventory modeling of systems:Multi-echelon techniques[M].2nd edBoston: John Wiley & Sons, 2004: 48-57. |
