对于初始备件来说,因为掌握的信息量少,缺乏备件的故障率信息,对于其需求的确定较为困难。目前常用的初始备件需求预测方法有:相似产品预计法[2-4]、备件保障概率法[5-7]、备件需求量概率分布预计法[8-9]等,这些方法已经在工程中得到了应用。但是随着装备部署部队,其可靠性会随着使用环境的变化发生改变,研制阶段确定的初始备件需求常常无法满足装备部署部队后的保障要求,影响了装备的完好率。
针对上述情况,为了提高初始备件需求预测精度,本文引入了相似系统理论(Similarity System Theory, SST)和Bayes方法。首先,提出基于特征重要性的系统相似度度量方法,初步确定备件的初始失效率;然后,以装备首次部署初期的实际故障数据为先验信息,结合装备使用阶段的备件消耗特性,利用Bayes方法得到后验失效率, 最后,综合初始失效率和后验失效率确定初始备件需求,尝试为初始备件需求确定问题提供一种新的方法。
1 备件需求量分析 参考国军标GJB 4355—2002[10],已知零部件在装备中的单机安装数N,累积工作时间t,失效率λ和备件保障概率P。备件需求量的基本计算公式为
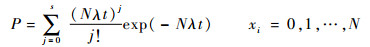 | (1) |
式中:s为装备中某零部件的备件需求量;P为在规定保障时间内,需要该备件时,不缺件(能得到它)的概率;j为递增符号,j从0开始逐一增加,直至某s值,使得P ≥规定的保障概率,该s值即为所求备件需求量。
由此可见,当装备中的单机安装数N,累积工作时间t和备件保障概率P确定的情况下,失效率λ决定备件的需求量。
2 初始备件配置方案分析 装备部署部队后使用环境随之改变,研制阶段确定的初始备件需求常常难以满足装备部署部队初期的保障要求。使用方亟需对初始备件需求方案进行调整。由此可见,初始备件的配置是一个逐步调整和优化的过程。为了能够及时准确地对初始备件需求方案进行优化调整,需要利用装备部署初期的可靠性数据,对研制阶段估计的失效率进行修正。
本文基于SST和Bayes方法给出初始备件方案调整优化方法。SST是根据功能相似装备在使用中所得到的经验(数据),对新设计装备的失效率参数进行估计,这种方法适用于具有相似可靠性数据的新装备在研制阶段用以预计其失效率。Bayes方法综合利用研制阶段的可靠性试验数据和使用阶段的可靠性数据对装备失效率进行估计,在可靠性评估中得到了广泛的应用。综合2种方法对备件失效率进行估计,进而确定装备初始备件需求。
3 初始备件需求确定方法 3.1 总体思路 首先根据SST初步确定备件的初始失效率;然后在实际使用数据的基础上,运用Bayes方法得到后验失效率,最后综合初始失效率和后验失效率,进而确定初始备件需求。总体思路如图 1所示。
 |
| 图 1 总体思路 Fig. 1 General idea |
| 图选项 |
3.2 基于SST的备件初始失效率确定 20世纪90年代,周美立和王浣尘[11-12]提出了SST,计算系统相似度的新理论。SST为备件初始失效率的确定提供了一种可靠方法。
定义1?相似要素:假设要素ai(i=1, 2,…, K)属于系统A,要素bj(j=1, 2,…, L)属于系统B,系统A、B有共同的属性(特征)S,且在数值上存在差异,则称要素ai和bj为相似系统A、B间的相似要素。
定义2?相似元:如果系统A、B间存在对应的相似要素(ai,bj),该集合便构成一个相似单元,称为相似元,记为u(ai, bj)。
若系统A、B间有n个相似元素,则2个相似元构成的集合,记为U,则有U=(u1, u2, …, un),在相似系统A、B中元素数量一定条件下,系统间相似元素的多少直接决定着由元素数量确定的相似程度,记为Qn,即
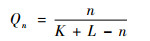 | (2) |
设相似元素有m个共有相似特征,依次为S1, S2, …, Sm。相似特征可用特征函数Uj(xi)表示,考虑相似元ui,记Uj(ai)为元素ai中特征Sj所对应的值,Uj(bi)为元素bi中特征Sj所对应的值,特征值的确定要依据元素的具体属性和特征而定。用n维空间度量,对应特征值比例系数记为
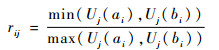 | (3) |
式中:0≤rij≤1,i=1, 2,…, n,j=1, 2,…, m,对于相似元素一切特征Sj都有Uj(ai)=Uj(bi),则rij=1。
假定相似元素共有m个特征,对于第i个相似元的m个特征值的比例系数可分别记为ri1, ri2, …, rim。设相似要素ai,bi的特征数目分别为k, l,相似元素值记为q(ui)n,则有
 | (4) |
每个特征对元素相似的影响程度不同,取特征权重为d1, d2, …, dm,则相似元素的特征相似程度记为q(ui)s,则有
 | (5) |
对于元素整体相似度,元素间有数量相似度,元素内有特征相似程度,根据典型并合算法[13],可给出相似元相似度q(ui)的计算式如下:
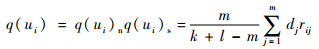 | (6) |
式中:
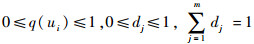
针对系统相似度,每一相似元值对系统相似度的影响可以不同,取特征权数分别为p1, p2, …, pm,给出相似元数值确定的相似度,记为Qc,即
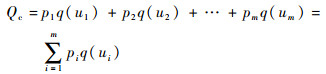 | (7) |
对于系统整体相似而言,系统间有数量相似度,系统内有元素相似程度,根据典型并合算法[13],得到系统相似度的计算式如下:
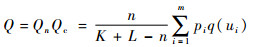 | (8) |
假设2个系统的相似度为Q,Q反映了新系统对老系统的继承性,设老系统的失效率为λe,则新系统的初始失效率为
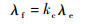 | (9) |
式中:kc为修正因子,可根据系统的相似度Qe,结合工程信息和专家经验来确定。
3.3 基于Bayes方法的备件后验失效率确定 Bayes方法的核心是Bayes定理[14]。Bayes定理可以实现通过收集到的数据对已有信息的更新。先验分布代表了试验前对待估参数的初始估计。在得到数据试验之后,可以利用“新的信息”对先验分布进行更新。由于更新后待估参数的概率分布反映了在得到实验数据之后对参数的认识,所以该分布被称为后验分布,数学上,Bayes定理可表示为
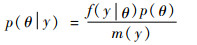 | (10) |
式中:p(θ|y)为后验密度函数,p(· |·)用来表示条件密度函数和;

由于式(10)中的m(y)与模型参数θ无关,因此,在式(10)中,m(y)被视为比例常数的一部分,并没有直接出现。将式(10)写为概率密度函数的形式,则有
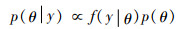 | (11) |
式中:符号“∝”表示两边仅相差一个不依赖于θ的常数因子。
通过上述分析可知,Bayes方法的核心是找到恰当的先验分布,如何确定先验分布的选取符合实际与否,可以通过共轭先验分布法确定。常用的先验分布及其共轭分布如表 1所示。
表 1 常用的先验分布及其共轭分布 Table 1 Commonly-used prior distribution and its conjugate distribution
| 先验分布(参数) | 共轭分布 |
| Binomial(π) | Beta |
| Exponential(λ) | Gamma |
| Gamma(λ) | Gamma |
| Multinomial(π) | Dirichlet |
| Multivariate Normal(μ,Σ) | Normal Inverse Wishart |
| Negative Binomial(π) | Beta |
| Normal(μ,σ已知) | Normal |
| Normal(σ,μ已知) | Inverse Gamma |
| Normal(μ,σ) | Normal Inverse Gamma |
| Pareto(β) | Gamma |
| Poisson(λ) | Gamma |
| Uniform(0, β) | Pareto |
表选项
假设备件寿命服从指数分布Exponential(λ),它的故障分布密度函数为f(t)=λe-λt,得到定数截尾的前r个失效时刻t1≤t2≤…≤tr(样本的前r个顺序统计量),似然函数为
 | (12) |
式中:
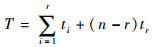
 | (13) |
式中:α>0为形状参数;β>0为尺度参数;均值和方差分别为E(λ)=α/β和Var(λ)=α/β2。
可知
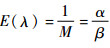
 | (14) |
先验分布中的未知参数称为超参数,怎样通过先验信息求得超参数是使用Bayes方法必须研究的问题。本文采用最大熵原则来确定2个超参数。
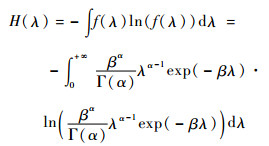 | (15) |
当α=1时,熵H(λ)的值达到最大[15],此时β=M,相应的先验分布为
 | (16) |
此时,后验分布为
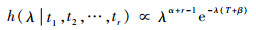 | (17) |
从式(17)出发,可得λ的Bayes估计为
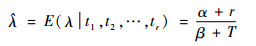 | (18) |
3.4 备件失效率组合预测模型 备件失效率组合预测模型为
 | (19) |
式中:w1、w2分别为初始失效率
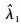
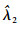
此时,当装备中的单机安装数N,累积工作时间t以及备件保障概率P全部确定以后,通过式(1)便能够确定使用阶段的初始备件需求量s。
4 实例分析 某种新设计的教练机,发动机系统某备件LLRU(外场可更换单元)由9个SSRU(内场可更换单元)构成(单机安装数均为1),构建失效率相似分析指标体系如图 2所示。收集到同类机种的可靠性预计值,如表 2所示。
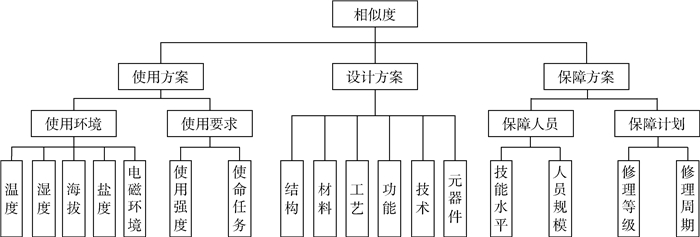 |
| 图 2 失效率相似分析指标体系 Fig. 2 Failure rate similar analysis index system |
| 图选项 |
表 2 SSRU1备件相似性分析 Table 2 Spare parts similarity analysis of SSRU1
| 失效率影响因素 | 使用环境 | 使用强度 | 使命任务 | 结构 | 材料 | 功能 | 保障人员 | 保障计划 |
| 特征权数β1 | 0.2 | 0.1 | 0.15 | 0.1 | 0.1 | 0.15 | 0.1 | 0.1 |
| 相似元相似度q(ui)s | 0.98 | 0.91 | 0.95 | 0.94 | 0.85 | 0.95 | 0.88 | 0.91 |
| 注:失效率相似度为0.93。 | ||||||||
表选项
以SSRU1为例,由工程研制信息和专家经验来确定特征权数和相似元相似度,利用相似系统原理计算失效率相似度,假设新设计的教练机和同类机种具有相同的失效率影响因素集,即k=L=n=8,结果如表 2所示。
据式(2)~式(8)计算出新老设备之间的失效率相似度为0.93,同理可得其他SSRU的失效率相似度,参考文献[10]中的算例,根据系统的相似度Qi,结合工程信息和专家经验得到平均故障间隔时间M预计值如表 3所示。
表 3 统计数据及预计值 Table 3 Statistical data and expected value
| 设备名称 | 老产品的M/h | 相似度 | 预计的M/h | λ/10-4 | 备注 |
| SSRU1 | 1 192.8 | 0.93 | 1 800 | 5.56 | 选用新型号,可靠性大大提高 |
| SSRU2 | 6 262 | 0.92 | 6 262 | 1.60 | 选用老产品 |
| SSRU3 | 2 087.3 | 0.86 | 2 087.3 | 4.79 | 选用老产品 |
| SSRU4 | 863.7 | 0.89 | 863.7 | 11.6 | 选用老产品 |
| SSRU5 | 6 000 | 0.91 | 6 500 | 1.54 | 在老产品的基础上,局部改进 |
| SSRU6 | 15 530 | 0.93 | 15 530 | 0.644 | 选用老产品 |
| SSRU7 | 6 520 | 0.85 | 7 000 | 1.43 | 在老产品的基础上,局部改进 |
| SSRU8 | 1 578.2 | 0.88 | 2 400 | 4.17 | 选用新型号,可靠性大大提高 |
| SSRU9 | 3 400 | 0.94 | 3 400 | 2.94 | 选用老产品 |
| LLRU | 253.3 | 292.05 | 3.42 |
表选项
通过SST计算出M=292.05,相应的初始失效率为0.003 42。在保障时间t0=600 h和备件保障概率P=0.86的情况下,根据式(1)可以得到初始备件需求量为4个。
假设收集到20台该型装备运行到100 h的故障数据,具体如表 4所示。
表 4 故障时刻数据 Table 4 Failure time data
| h | |||||
| 装备序号 | 1 | 2 | 3 | 4 | 5 |
| 故障时刻 | 9.28 | 25.8 | 39.6 | 56.8 | 77.4 |
表选项
注意到有15台装备未发生故障,利用Bayes方法处理该组数据,可以得到后验失效率为0.003 01。取初始失效率的权重系数w1和后验失效率的权重系数w2均为0.5。得到备件失效率为0.003 215。在保障时间t0=600 h和保障概率P=0.86的情况下利用式(1)可以确定该组件应配置3件备件就能满足装备部署初期的保障要求。
5 结论 1) 采用基于特征重要性的系统相似度度量方法,初步确定备件的初始失效率,使用SST充分利用相似装备的数据信息来确定初始失效率,比单纯使用试验数据更合理。
2) 采用Bayes方法,以装备的实际使用数据为依据,得到备件的后验失效率,该方法反应了装备的独有特性,计算简便,可以推广到其他常见分布。
3) 综合考虑初始失效率和后验失效率确定装备的初始备件需求。该方法在确定初始备件需求的过程中,实现了主观与客观相结合,全面考虑了研制阶段影响初始备件需求的主要因素,既合理地反映了新装备的独有特性,又有效地综合了历史信息,提高了初始备件需求预测精度。
参考文献
| [1] | U.S.Department of Defense.Defense and program-unique specifications format and content:MIL-STD-961E(1)[S].Washington, D.C.:U.S.Department of Defense, 2008:130-135. |
| [2] | 夏秀峰, 董彦军. 基于改进马尔科夫模型的航空备件需求预测[J].兵工自动化, 2013, 32(11): 39–43. XIA X F, DONG Y J. Demand prediction for spare parts of aviation based on improved Markov model[J].Ordnance Industry Automation, 2013, 32(11): 39–43.DOI:10.7690/bgzdh.2013.11.010(in Chinese) |
| [3] | 徐宗昌, 张永强, 呼凯凯, 等. 备件携行量研究方法综述[J].航空学报, 2016, 20(4): 944–948. XU Z C, ZHANG Y Q, HU K K, et al. Survey on amount configuration methods of carrying spare parts[J].Acta Aeronautica et Astronautica Sinica, 2016, 20(4): 944–948.(in Chinese) |
| [4] | 徐飞, 杨士英, 魏祥生, 等. 基于改进灰色预测模型的雷达备件消耗预测[J].雷达科学与技术, 2015, 13(6): 610–615. XU F, YANG S Y, WEI X S, et al. The forecast of radar spare part consumption based on the improved gray forecasting model[J].Radar Science and Technology, 2015, 13(6): 610–615.(in Chinese) |
| [5] | 林国宝, 黄照协, 王齐. 基于保障概率的初始备件需求预测方法研究[J].计算机与数字工程, 2015, 43(2): 249–251. LIN G B, HUANG Z X, WANG Q. Initial spare parts forecast method based on supportability[J].Computer & Digital Engineering, 2015, 43(2): 249–251.(in Chinese) |
| [6] | 周伟, 郭波, 张涛. 两级供应关系装备常用备件初始配置模型[J].系统工程与电子技术, 2011, 33(1): 90–93. ZHOU W, GUO B, ZHANG T. Initial configuration model for common equipment parts based on two class supply relationship[J].Systems Engineering and Electronics, 2011, 33(1): 90–93.(in Chinese) |
| [7] | 肖波平, 康锐, 王乃超. 民机初始备件方案的优化[J].北京航空航天大学学报, 2010, 36(9): 1057–1061. XIAO B P, KANG R, WANG N C. Optimal of initial spares scenario in civil aviation[J].Journal of Beijing University of Aeronautic and Astronautic, 2010, 36(9): 1057–1061.(in Chinese) |
| [8] | 谢君, 王红卫. 基于更新过程的多阶段备件需求模型[J].海军工程大学学报, 2009, 21(1): 1–4. XIE J, WANG H W. Calculation models of spare demand for multi-period inventory system based on renewal process[J].Journal of Naval University of Engineering, 2009, 21(1): 1–4.(in Chinese) |
| [9] | BLANCHARD B S. Logistics engineering and management[M].Upper Saddle River: Prentice Hall, 2004: 36-96. |
| [10] | 中国人民解放军总装备部. 备件供应规划要求: GJB 4355-2002[S]. 北京: 中国人民解放军总装备部, 2003. PLA General Armament Department.Spares provisioning requirements:GJB 4355-2002[S].Beijing:PLA General Armament Department, 2003(in Chinese). |
| [11] | ZHOU M L. Principles and practice of similarity system theory[J].International Journal of General Systems, 1994, 23(1): 39–48.DOI:10.1080/03081079408908028 |
| [12] | 周美立, 王浣尘. 相似系统的分析与度量[J].系统工程, 1996, 14(4): 1–4. ZHOU M L, WANG H C. An analysis and measure of similar systems[J].System Engineering, 1996, 14(4): 1–4.(in Chinese) |
| [13] | 王浣尘. 可行性研究和多目标决策[M].北京: 机械工业出版社, 1986: 15-22. WANG H C. The feasibility study and multi-objective decision[M].Beijing: China Machine Press, 1986: 15-22.(in Chinese) |
| [14] | HAMADA M S, WILSON A G, REESE C S, et al. Bayesian reliability[M].Berlin: Springer, 2008: 12-16. |
| [15] | 李贤平. 概率论基础[M].北京: 高等教育出版社, 2010: 212-214. LI X P. The basic of probability theory[M].Beijing: Higher Education Press, 2010: 212-214.(in Chinese) |
