传统算法很难对上述大规模动态图进行有效分析和挖掘。首先,由于图的规模庞大,导致在图的计算上的时间过长。其次,程序往往不能获取图的全部数据,而只能获取数据的一部分。例如社交网络图,通常只能通过爬虫抓取获得部分数据。另外,即使有的图规模略小一些,但是计算某些图的重要的度量值需要的处理时间非常长(例如生物细胞科学的实验)。因此,需要采用并行处理的技术提高图的处理能力。
目前大部分的研究聚焦在基于图的数据关系结构分析。目前图挖掘算法针对特定的数据集处理一类特定的图,或者把一种具体的图算法应用到不同的领域。但是,这些算法都不能很好地解决图挖掘的扩展性问题,尤其是大规模动态图的异常检测问题。例如Facebook拥有8亿用户,用户每分钟发表 50万条评论,超过29万条状态更新。这样包含上亿结点、每分钟产生几十万边的图的分析和异常检测问题都没有得到很好地解决。另外,除了图的结构信息,语义信息(如标签、权重和属性等信息)也能辅助检测图异常,提高检测的准确性。
异常行为通常模仿正常的行为模式,所以越接近于正常模式的异常,越难以分辨。因此本文把与正常模式相似的近似模式称为异常模式。在基于图的表示中,异常模式通常在正常模式上进行修改,例如添加边和结点、删除边和结点或修改结点属性信息。目前基于图的异常检测(Graph Based Anomaly Detection, GBAD)[2]首先使用一种基于最小描述长度的压缩算法来寻找正常模式,然后分析与正常模式相近的模式,计算其异常值,最后判断这些相近的模式是否为异常模式。虽然这个算法在很多领域被广泛应用[3],但是算法的可扩展性问题,尤其是处理百万级结点的图的算法效率问题没有得到很好地解决。大规模图随着时间不断演化,这也加剧了分析的困难——正常模式随着时间或者事件触发也会发生变化。为解决此问题,本文提出了针对大规模图数据的增量并行式异常检测的DPADS(Dynamic Parallel Anomaly Detections)算法,该算法可以更有效的处理大规模静态以及动态流图的异常检测。
1 相关工作 根据早期的图异常检测的研究,Noble和Cook[4]探讨图结构的异常。他们先基于正常模式对图进行压缩,后把余下的结构定义为异常。Akoglu等[5]处理了大规模图的异常检测问题,但是他们的目标是检测异常的结点。文献[4-5]都认为图是静态的。
一种解决大规模图的算法是把图看做边的数据流,每次处理图的一个或者多个边。研究者在异常检测领域提出一些不同的算法来处理图的边数据流。其中一种被称为“semi-streaming model”的算法,可以处理不能把所有边存储到内存的大规模图。Feigenbaum等提出了semi-streaming常量近似算法,来处理无权重和带权重图的匹配问题,同时也扩展应用到二分图[6]。其他的研究则把此算法扩展,来解决不同的图问题,例如有向图的最短路径问题、使用中间的临时流来解决特定问题等[7-9]。总之,这些算法分析了可用的内存和访问整个图所需访问硬盘次数这两者之间的关系,并根据实际情况进行策略调整。
基于k-core结构的图结构中的模式识别和异常检测[10]通常用来进行层级结构分析,图可视化和图聚类。它探讨了常见的模式与k-core之间的3种关系并设计相关算法,并证明这些模式有效地处理大规模图数据。随时间变化的图数据多层级异常检测[11]提出一种建模和分析的框架检测标签的异常。它通过概率模型描述子图和通过相关的层级模型同时检测异常。此算法不仅能检测结构异常,也能检测标签上下文中的事件。一种图划分算法[12]有效地检测图数据流规模的异常。文献[13]归纳总结了基于图的异常检测和描述。
有些算法检测图数据流中的异常,其目标是通过分析边数的统计信息识别异常的子图簇,而不是发现图或图数据流中结构的异常。另外一些算法尝试使用基于整个图的算法[2]来发现异常子图[13],但这类算法没有解决可扩展性问题。
另外,大多数异常检测算法使用监督的学习算法,需要数据提前打好标签、做好分类,然后再训练模型,进行预测。而实际情况是大多数时候不能提前知道异常或者正常的相关信息,因此需要一种无监督的算法来检测那些看起来像正常、合法但实际上结构不同的异常模式。
2 DPADS算法的流程及分析 DPADS算法把静态图的异常检测算法GBAD和并行异常检测(Parallel Anomaly Detection, PLAD)算法扩展到大规模动态图的异常检测中,如图 1所示,Ti-1、Ti、Ti+1为时间滑动窗口。本文定义3种基本类型图的异常:添加、修改和移除。添加异常是正常模式增加了结点或边。修改异常包含了一个结点或边的意外标签。移除异常的子结构比正常子结构缺少了边或结点。
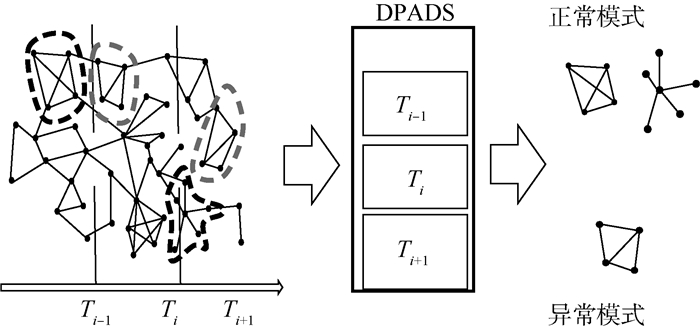 |
| 图 1 DPADS算法并行处理子图 Fig. 1 Parallel processing subgraphs of DPADS algorithm |
| 图选项 |
DPADS算法检测图的异常基于这样的思想:异常的子结构(或子图)是正常模式的结构变种(正常模式边和节点的增加或者缺失)。假设d(G1, G2)表示2个图G1和G2之间的结构差异度量,计算把图G1转化为G2的同构图的计算量(添加、删除点与改变标签的变化数量),衡量G1和G2之间的差异。
定义1??在图G中,正常模式S可由最小描述长度(Minimum Description Length,MDL)原理来判定,并最小化以下目标函数:
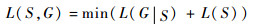 |
式中:G为整个图;L(G|S)为使用S压缩G之后的描述长度;L(S)为正常模式S的描述长度;S为正常模式。MDL[14]原理即要求模型的总描述长度最小。正常模式检测的MDL原理具有2个重要的性质:
1) 当有2个模式都能很好地匹配原始图时,MDL原理选择“最简单”的模式,即选择压缩率更高的描述。这也反映了奥卡姆剃刀对简单理论的优先选择。
2) MDL原理是一致的。随着数据量的不断增加,中间过程产生的正常模式收敛于真正的正常模式。
定义2??图G1和G2之间的差异:
 |
定义3??一个子结构SA在图G中为异常如果(0 < d(SA, S) < D)且(0 < P(SA|S, G) < P)。式中S为G中的正常模式,D定义了异常模式SA到正常模式S的最大差异,P(SA|S, G)为图G在正常模式S的压缩下SA为异常的概率,P限定了SA为异常的最大概率。
定义4??在图G中,基于正常子结构S的异常子结构SA的值R=d(SA, S)P(SA|S, G)。根据实验分析R值在(0, 2.6)之间,表示SA为异常的子结构可能性越大。
若找到一个正常模式S和与其相似的异常模式SA,则可迭代地找到其他的异常。先使用正常模式对原始图进行压缩,例如把正常模式替换成一个带有新标签的结点。再在压缩之后的图上寻找正常模式S和相关的异常SA,这个过程可以进行多次迭代以找到更多的正常模式和异常模式,直到遍历到整个图,当图进一步压缩时还能够进行不同级别的异常检测。
2.1 DPADS算法流程图及删除边的处理 本文提出了DPADS算法,它以n个子图为输入,可以是静态图的切分,也可以是随时间获取的图的一部分。DPADS主要分为2个阶段:初始化和迭代处理。初始化阶段的主要目标是在n个子图中找出正常模式S及其相关的异常模式。首先,并行处理n个子图,分别检测top-M个正常模式,一共得到n×M个正常模式。然后,判定正常模式集合S。最后根据正常模式S检测异常的结构。迭代处理阶段的主要目标是迭代分析新获取的数据的结构异常。首先,把活动窗口向后移动一个窗口,让新获取的子图包含在滑动窗口内。其次,在新的子图中检测top-M正常模式。然后,从滑动窗口中的所有子图中判定正常模式S′。如果S′=S,只需检测新子图里的异常;否则,窗口里的每个子图都基于正常模式S′检测异常结构。接下来,对每个异常子结构计算R值,值最小的子结构判定为异常结构。最后,重复迭代过程。DPADS算法流程图如图 2所示。
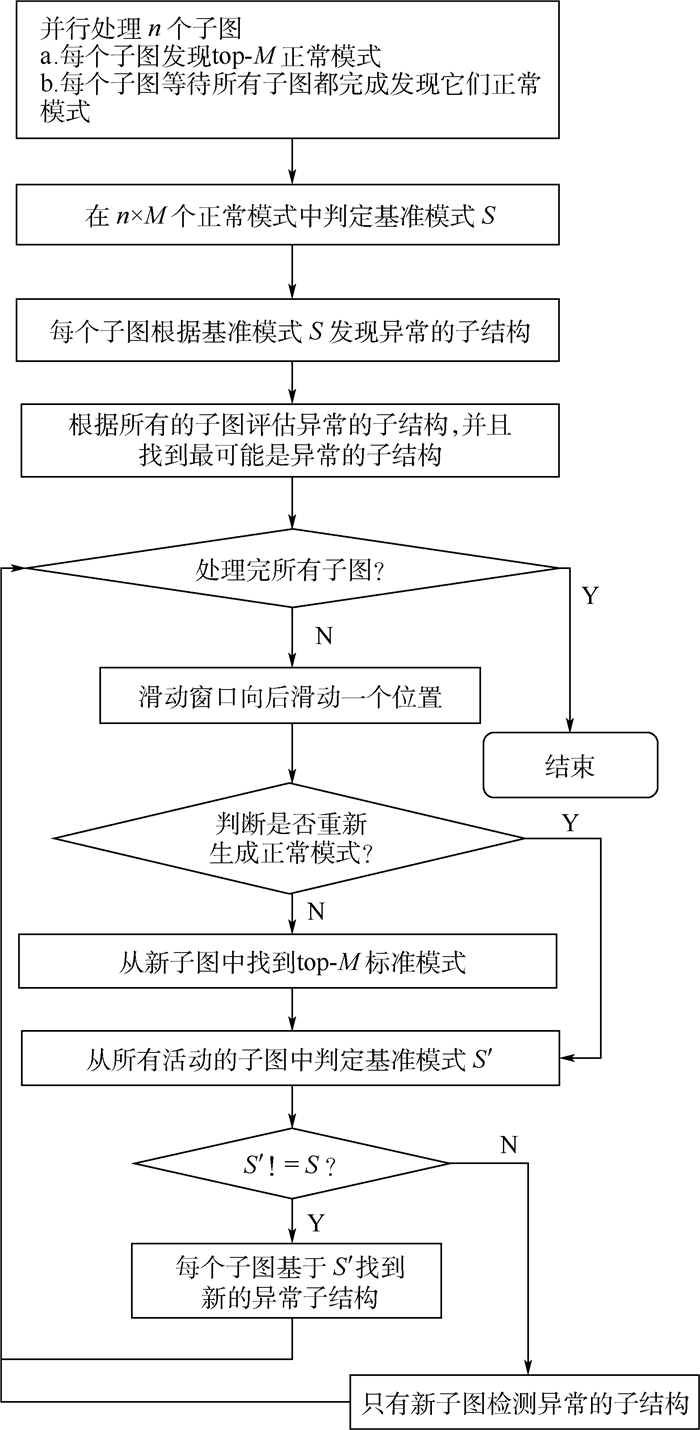 |
| 图 2 DPADS算法流程图 Fig. 2 Flowchart of DPADS algorithm |
| 图选项 |
1) 初始化
步骤1??并行处理n个子图:
a.每个子图发现top-M正常模式。
b.每个子图等待所有子图都完成发现它们正常模式。
步骤2??在n×M个正常模式中判定基准模式S。
步骤3??每个子图根据基准模式S发现异常的子结构。
步骤4??根据所有的子图评估异常的子结构,并且找到最可能是异常的子结构。
2) 迭代处理
步骤5??处理新的子图:
a.如果序号在最前面的子图超过了阈值T(基于一定的标准,例如可处理的子图数量,或者子图的时间戳),那么把这些子图移除,不进行下一步分析。
b.判断是否重新生成正常模式,若为TRUE,则跳转到步骤d。
c.否则,从新子图中找到top-M标准模式。
d.从所有活动的子图中判定基准模式S′。
e.如果(S′!=S),每个子图基于S′找到新的异常子结构。
f.否则只有新子图检测异常的子结构。
g.评估所有子图的异常子结构,并且找到最可能是异常的子结构。
h.重复上述过程。
PLAD算法[15]解决了图随着时间不断插入新的结点、边和属性过程中的异常检测问题,但它并没有考虑已有的结点、边和属性随时间或环境变化而移除的过程。所以本文对以上的算法进行改进以适应动态图的情景。算法的主要思想是维护正常模式,因此可以根据正常模式检测异常。但是图随着时间动态更新会导致正常模式发生变化或者重新检测,这一过程耗时较长。当前目标是尽量少地重新检测正常模式[16]。在移除边e之后,需要保证
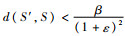
2.2 算法分析 针对DPADS算法,描述检测正常模式的算法所需要的信息量可以分为正常模式描述长度代价L(S)和图G的描述长度代价L(G|S)。首先简要介绍用到的符号,Si为S中独立的正常模式,n(Si)为Si的数量,ni(a)为Si中属性a的数量,ni和ei分别为Si中的结点数和边数。
1) 正常模式描述代价
正常模式描述代价指的是描述获得正常模式算法所需要的信息量,描述复杂度由以下部分构成:
A.结点个数N,属性数量L,需要的信息量为(lb N+lb L)bit。
B.记录正常模式的个数M,需要lb M bit。
C.记录在寻找正常模式过程中,对l个属性进行检测,需要lb l bit。
D.描述每个正常模式中的结点信息,需要
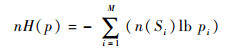 |
式中:pi=n(Si)/n;H(p)为香农熵理论,p为概率。
E.描述正常模式之间的连接关系,理论上它们之间的连接越少越好,eij表示正常模式之间的边个数。
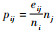
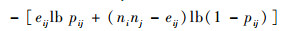 |
F.描述每个正常模式中所包含的属性信息,需要
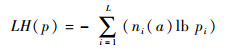 |
式中:pi=ni(a)/L。
2) 图描述代价
图描述代价指的是在给定正常模式情况下,对原始图进行压缩描述所需要的代价。假设正常模式中的结点和边服从0-1分布,且节点相互独立,则根据香农熵理论,对正常模式S中的元素x进行描述需要花费n(S)H(p(x)) bit的信息量,其中
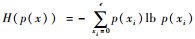
在正常模式内部,如果结点及其边和属性联系紧密,则其相应的熵值比较小,所需要的描述信息量也较小。
因此,基于MDL描述的图的复杂度由两部分组成:
A.用期望来描述正常模式内部的联系,表示正常模式中结点之间的关系。正常模式S的结点数为n,边数为e,因此,pi=p(S=1)=e/n2,描述所需要的代价为
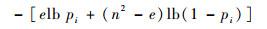 |
B.对每个正常模式中的属性信息,设每个正常模式中属性包含ai的结点个数n(ai),则p(ai)=n(ai)/ni,则在每个正常模式中的属性描述代价为
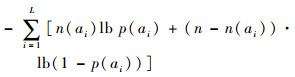 |
根据以上的分析,总的正常模式描述代价函数为
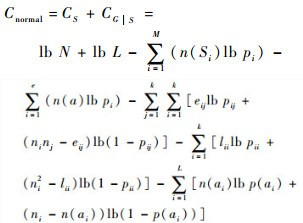 |
式中:CS和CG|S分别为正常模式和基于最小原理用正常模式S描述图G的描述代价函数。
那么,n×M个正常模式与其异常模式(3种情况)的描述代价函数为
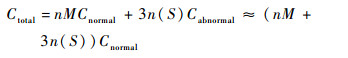 |
式中:n(S)为正常模式S的个数;Cabnormal为异常模式描述代价函数。
3 实验和评估 本节在多个真实的数据集上验证第2节提出的算法,包括效率、准确性和误报性。从斯坦福大学SNAP[17]项目中选取了3个数据集:无向图、有向图和有向时序图进行算法验证,数据的详细信息如表 1所示。
表 1 实验数据集 Table 1 Experimental data sets
| 数据名称 | 类型 | 结点个数 | 边个数 |
| YouTube | 无向图 | 1 134 890 | 2 987 624 |
| LiveJ | 有向图 | 484 751 | 68 993 773 |
| Math | 有向时序图 | 24 818 | 50 650 |
表选项
3.1 效率 在3个数据集上的运行时间总体上随着数据集的大小而变化。图 3给出本文提出算法DPADS与对比算法PLAD在运行时间t上的比较:DPADS算法在运行时间上优于现有的算法。DPADS算法不仅处理图的增量式增加而且还解决现有的节点和边随时间减少的演化流式图的异常检测,通过提前判断正常模式的变化,减少整个异常检测过程的时间。
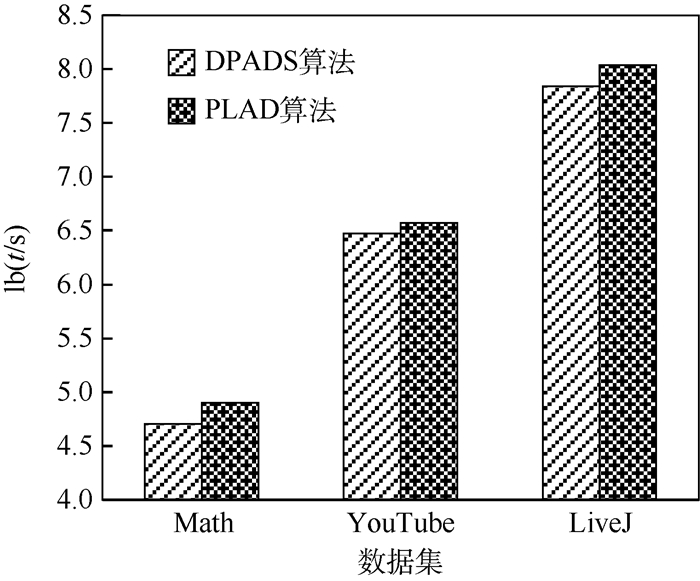 |
| 图 3 DPADS与PLAD算法运行时间比较 Fig. 3 Comparison of running time betweenDPADS and PLAD algorithms |
| 图选项 |
3.2 准确率、召回率和ROC 异常检测的重要指标是PR(Precision Recall)曲线和ROC(Receiver Operating Characteristic)曲线。异常检测的准确率为检测到异常个数与总样本数之比;召回率为检测到的异常个数与总异常个数之比。从图 4中可以看出,理想结果由空心三角表示,准确率和召回率都是100%。本文提出的DPADS算法检测异常准确率平均达到96%,即检测到的异常模式中96%都是异常模式;召回率的平均值为85%,即85%的异常都可以检测到。由于DPADS算法首先对图进行划分,而且划分时只按照时间或获得边的顺序划分,并没有考虑到图的连接性和子图的相关性,所以导致准确率没有达到100%。另外,由于动态图随时间不断变化,正常模型也随之不断变化,导致召回率没有达到100%。
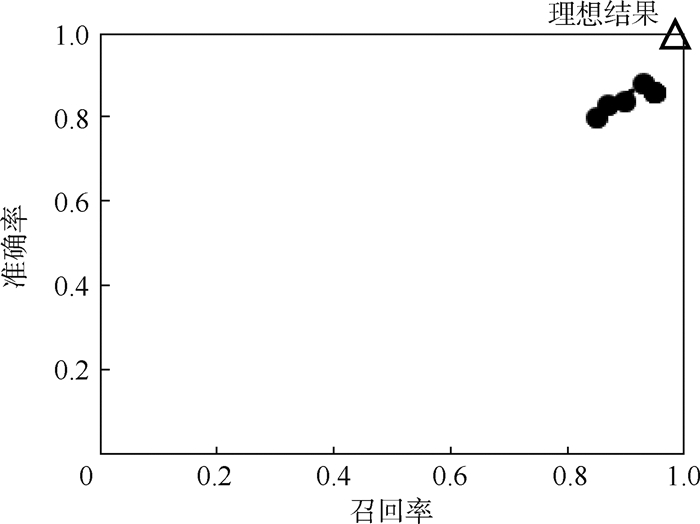 |
| 图 4 准确率和召回率 Fig. 4 Accurate rate and recall rate |
| 图选项 |
ROC曲线是一种对于灵敏度进行描述的功能图像。ROC曲线可以通过描述真阳性率(True Positive Rate,TPR)和假阳性率(False Positive Rate,FPR)来实现。最好的检测方式是在左上角的点,即ROC空间坐标轴(0, 1)点,它代表 100%灵敏(没有假阴性)和100%特异(没有假阳性)。完全随机的检测的任一结果对应的准确度都是50%。如图 5所示,虚线表示真阳性率和假阳性率都为0.5的随机结果,在此虚线上方的结果都比随机结果的效果好;坐标上(0,1)点的实心三角表示理想的结果,3个实心圆点分别是3个数据集的ROC结果,分别为0.95、0.94和0.98。这3个值都接近(0,1)点,即都接近理想的结果。
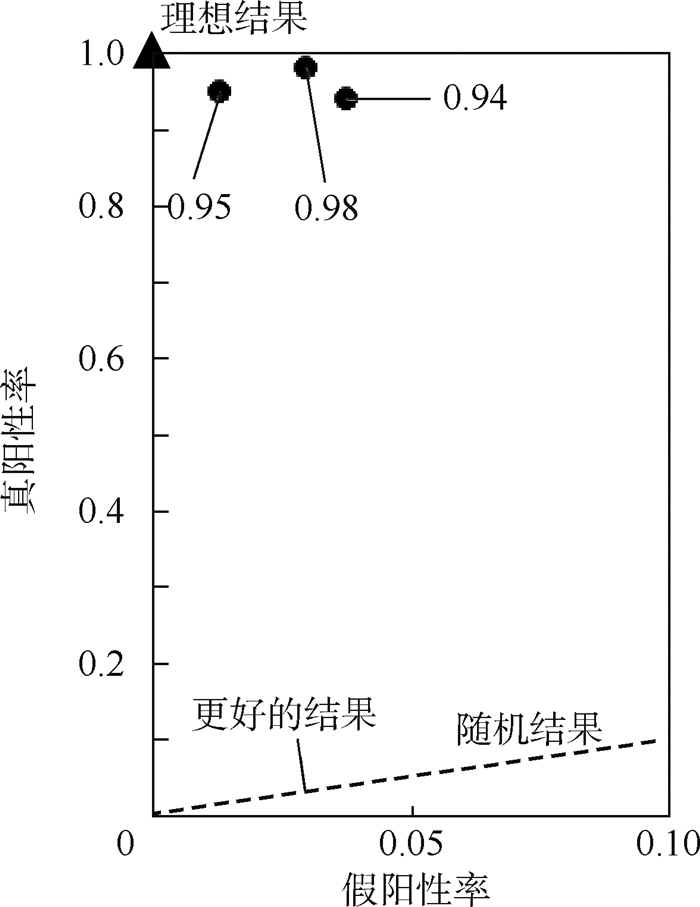 |
| 图 5 ROC曲线 Fig. 5 ROC curve |
| 图选项 |
3.3 M值对准确率和召回率的影响 M值表示每个子图中正常模式选取的个数,即top-M。正常模式根据L(S)+ L(G|S)计算的值进行从小到大排序,前M个作为top-M的正常模式。M是根据经验设定的固定值。如果M取值过小,导致每次检测没有包含足够的正常模式,则准确率和召回率下降。如果M取值到一定范围,不会影响算法的准确率和召回率,如图 6所示。
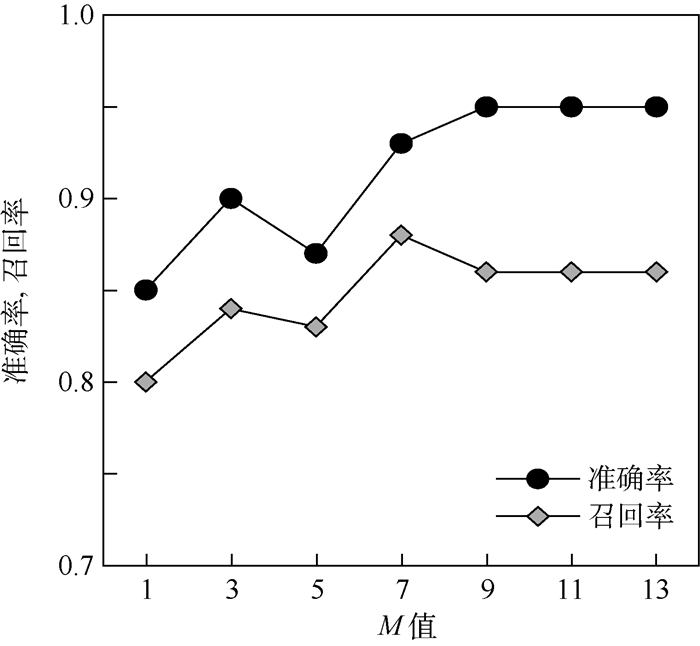 |
| 图 6 M值对准确率和召回率的影响 Fig. 6 Influence of M value on accurate rate and recall rate |
| 图选项 |
4 案例分析 本文使用图生成器产生包含两百万边的稀疏图。虽然这个图的规模没有达到“大数据”典型的上十亿的结点,但是DPADS算法能快速处理“大数据”规模的图。
1) 静态图的异常检测算法
图包含一个特定的正常子图由10个结点(v1, v2, …, v10)和9条边(e1, e1, …, e9)组成,随机产生多个级别的异常子结构插入到图中。在整个图上运行静态图异常检测算法后,异常子结构包含一个多余结点VW和多余边EW,连接到正常模式上,如图 7所示。但是正常模式和异常子结构花费了76 356 s(21.21 h)的运行时间,这在现实环境中运行时间太长,不能接受。
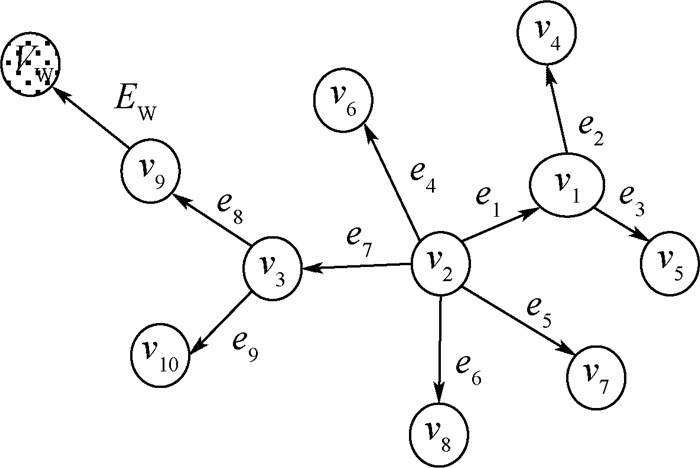 |
| 图 7 正常模式和异常模式 Fig. 7 Normal pattern and abnormal pattern |
| 图选项 |
2) DPADS算法
为了验证本文提出的增量式异常检测算法在图的流数据上的有效性,本文把DPADS算法应用到合成数据集上。在此实验中,原始图划分成100个小图,每个图包含大约20 000条边。初始化阶段随机选取20(T)个小图。选取20个小图的目的是得到初始化的正常模式和异常模式。然后并行处理它们,花费40 s,每个小图得到3(M)个正常的模式。
在处理过程中即使小图采用顺序方式处理,总共花费486 s完成20个小图的正常模式检测。然后,对60(T×M)个正常模式进行分析和整合,确定正常模式集S。最后,根据正常模式S检测异常模式SA,这一步骤花费156 s完成。在迭代阶段,本文使用T=20个作为处理窗口的大小(把20个小图都放到内存中)。然后依照算法进行多次迭代。
实验结果表明,本文算法可以应用到大规模图中。该算法在图流数据上检测到的异常模式与在整个图上检测到的异常模式是一致的,而在流数据上运行完成时间是3 017 s(在整个图上运行静态图算法花费76 356 s)。每个小图的运行时间如图 8所示,含有异常模式的小图由菱形点标出,没有检测到异常的小图由圆点表示。
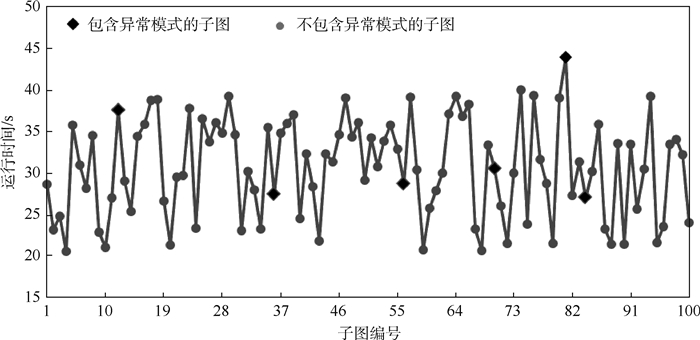 |
| 图 8 DPADS算法在每个子图上的运行时间并标记发现异常的子图 Fig. 8 Running time of DPADS algorithm in each subgraph and marked subgraphs with abnormal pattern |
| 图选项 |
值得指出的是,窗口的大小(保留在内存中小图的个数)也影响了检测异常模式的时间。在检测结束时,异常的子结构被认为是异常模式。但是,如果异常模式在前面的小图出现,而窗口向后滑动,前面的小图不在窗口范围内(T=20个),那么不能检测到这样的异常结构。这符合处理流数据的“概念漂移”,因此检测到的异常模式在新的数据到来之前变少。本文还设置不同的窗口大小并进行实验(初始过程子图的个数T),可以发现:
1) T=1个时,最新的小图总是检测到当前的异常子模式(如果存在)。
2) T=5个时,由于插入的异常模式比较少,窗口中仅有一个小图包含一个异常子结构,使得新的子图总是包含当前的最可能为异常的子结构。
3) T=10个时,当异常子结构在小图 85发现的时候,它的异常值低于之前的异常子结构的异常值,所以变成了当前的异常模式(当T=15个时,结果相同)。
除了准确率之外,运行时间也受到窗口大小T的影响,如图 9所示。由于并行处理的小图增加,结果显示运行的总体时间随着窗口大小T的增加而减少。
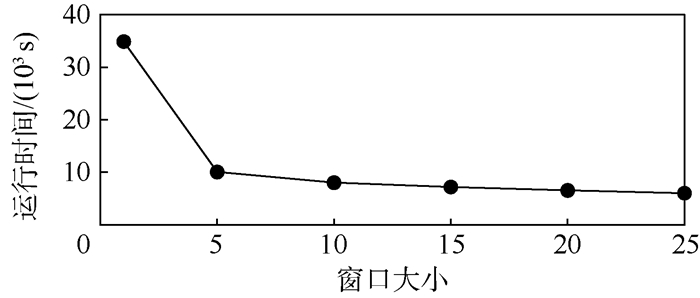 |
| 图 9 DPADS算法在合成数据集上随窗口大小变化的运行时间 Fig. 9 Running time of DPADS algorithm on synthetic datasets with different windows size |
| 图选项 |
5 结论 本文提出大规模动态图的异常检测算法DPADS,贡献如下:
1) 算法大大缩短了运行时间,例如处理结点数为一百万,边数量为三百万的动态图的运行时间为5 h,而其他算法运行时间为21 h。
2) 算法可实现较为优异的检测性能,例如处理边数量约七千万动态图数据检测异常结构准确率达到96%,召回率达到85%。
3) 滑动窗口大小约束了并行处理子图的数量,滑动窗口越大,算法运行时间越少。
4) 动态图不仅由结点和边随时间不断增加,而且还会不断减少。算法先增量并行处理大规模动态图的增加模式,再在此基础上处理边和结点减少的情况。
为使本文提出的算法进一步提高准确率和召回率,仍需要优化正常模式的检测和异常模式的参数。
参考文献
| [1] | AHMED N K, NEVILLE J, KOMPELLA R. Network sampling:From static to streaming graphs[J].ACM Transactions on Knowledge Discovery from Data(TKDD), 2014, 8(2): 7:1–7:56. |
| [2] | EBERLE W, HOLDER L. Anomaly detection in data represented as graphs[J].Intelligent Data Analysis, 2007, 11(6): 663–689. |
| [3] | EBERLE W, HOLDER L, GRAVES J. Insider threat detection using a graph-based approach[J].Journal of Applied Security Research, 2011, 6(1): 32–81. |
| [4] | NOBLE C C, COOK D J. Graph-based anomaly detection[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM Press, 2003: 631-636. |
| [5] | AKOGLU L, MCGLHON M, FALOUSTSOS C. OddBall: Spotting anomalies in weighted graphs[C]//Proceedings of the 14th Pacific-Asia conference on Advances in Knowledge Discovery and Data Mining. Berlin: Springer-Verlag, 2010, 3: 410-421. |
| [6] | FEIGENBAUM J, KANNAN S, MCGREGOR A, et al. On graph problems in a semi-streaming model[J].Theoretical Computer Science, 2005, 348(2-3): 207–216.DOI:10.1016/j.tcs.2005.09.013 |
| [7] | DEMETRESCU C, FINOCCHI I, RIBICHINI A. Trading off space for passes in graph streaming problems[J].ACM Transactions on Algorithms(TALG), 2009, 6(1): 6:1–6:17. |
| [8] | AGGARWAL G, DATAR M, RAJAGOPALAN S, et al. On the streaming model augmented with a sorting primitive[C]//Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science(FOCS). Washington, D. C. : IEEE Computer Society, 2004: 540-549. |
| [9] | SARMA A, GOLLAPUDI S, PANIGRAHY R. Estimating PageRank on graph streams[C]//Proceedings of the 27th ACM Sigmod-Sigact-Sigart Symposium on Principles of Database Systems. New York: ACM Press, 2008: 69-78. |
| [10] | SHIN K, ELIASSI-RAD T, FALOUTSOS C. CoreScope: Graph mining using k-core analysis-Patterns, anomalies and algorithms[C]//2016 IEEE 16th International Conference on Data Mining (ICDM). Washington, D. C. : IEEE Computer Society, 2017: 469-478. |
| [11] | BRIDGES R A, COLLINS J P, FERRAGUT E M, et al. Multi-level anomaly detection on time-varying graph data[C]//2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM). New York: ACM Press, 2016: 579-583. |
| [12] | EBERLE W, HOLDER L. A partitioning approach to scaling anomaly detection in graph streams[C]//2014 IEEE International Conference on Big Data. Washington, D. C. : IEEE Computer Society, 2014: 17-24. |
| [13] | AKOGLU L, TONG H, KOUTRA D. Graph based anomaly detection and description:A survey[J].Data Mining and Knowledge Discovery, 2015, 29(3): 626–688.DOI:10.1007/s10618-014-0365-y |
| [14] | 吴烨, 钟志农, 熊伟, 等. 一种高效的属性图聚类算法[J].计算机学报, 2013, 36(8): 1704–1713. WU Y, ZHONG Z N, XIONG W, et al. An efficient method for attributed graph clustering[J].Chinese Journal of Computers, 2013, 36(8): 1704–1713.(in Chinese) |
| [15] | EBERLE W, HOLDER L. Incremental anomaly detection in graphs[C]//2013 IEEE 13th International Conference on Data Mining Workshops. Washington, D. C. : IEEE Computer Society, 2013: 521-528. |
| [16] | EPASTO A, LATTANZI S, SOZIO M. Efficient densest subgraph computation in evolving graphs[C]//Proceedings of the 24th International Conference on World Wide Web. Geneva: International World Wide Web Conferences Steering Committee, 2015: 300-310. |
| [17] | YANG J, LESKOVEC J. Defining and evaluating network communities based on ground-truth[C]//Proceedings of the ACM SIGKDD Workshop on Mining Data Semantics. New York: ACM Press, 2012, 3: 1-3: 8. |
