传统的惯性/天文组合导航采用捷联惯组和星敏感器两者相组合的方法,利用星敏感器高精度定姿特性,通过卡尔曼滤波原理,抑制因陀螺漂移而造成的姿态角发散误差,同时估计出陀螺的常值漂移并进行补偿。文献[1]提出一种基于弹道导弹主动段状态转移阵的误差估计方法,有效地解决了关机点时刻速度和位置误差较大的问题,但由于星敏感器无法从根本上消除加速度计常值偏置等因素对系统的影响,因此无法保证后续飞行中速度、位置误差收敛。针对该问题近些年涌现出一些新方法,旨在改善定位误差,比如文献[2-3]在全面最优组合校正模式下对基于星光折射间接敏感地平的组合导航方法开展研究,实现了高精度定位,但就如何保证星敏感器始终扫描平流层获取折射星的问题工程上尚未实现。文献[4]通过直接敏感地平观测信息并利用高度差法,设计了一种气压高度表辅助的天文/惯性位置组合导航方案,虽然可以提高机载组合导航系统的整体定位精度,但定姿精度远不如星敏感器且不适用于弹道导弹。
雷达高度表(RA)作为一种主动式距离传感器,可分为激光雷达与无线电雷达。随着制导导航与控制技术在深空探测、航天航空的迅猛发展,雷达测距技术己经成功应用于轨道测量、弹道修正、卫星定位、交会对接、巡航制导、航天着陆、大地测量、微波遥感等方面[5-6]。与合成孔径雷达(SAR)适用于末制导微波成像不同[7],RA结构简单,可为稳定飞行平台提供精准的高度测量信息,适用于弹道导弹中段及末段飞行环境。本文针对弹道导弹中段飞行过程中导航精度偏低的问题,在SINS/CNS组合的基础上,提出一种基于雷达高度表的量测模型,引入新的位置量测量,在姿态机动的条件下,利用非线性扩展卡尔曼滤波(EKF)构建SINS/CNS/RA组合导航系统,以获取更高的速度、位置精度。
1 SINS与RA高程差量测模型 导弹在飞行过程中,通过向地球反射表面(海平面或地表平面)发射一系列雷达脉冲,由弹上雷达信号接收机测得回波信号后,可根据时间间隔Δt得到雷达高度表测量高度H′为[8]
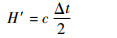 | (1) |
式中:c午磁波传播速度。
为了获得雷达高度表测得的海拔观测高度Ho,需在实测值H′的基础上进行高度补偿,即
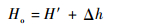 | (2) |
式中:补偿值Δh由当地地表海拔等因素决定[9]。弹道导弹的惯性导引通常以发射惯性系(以下简称l系)作渭航坐标系,如图 1所示,Re伪地地球半径,Re0为发射点至地心Oe的距离。
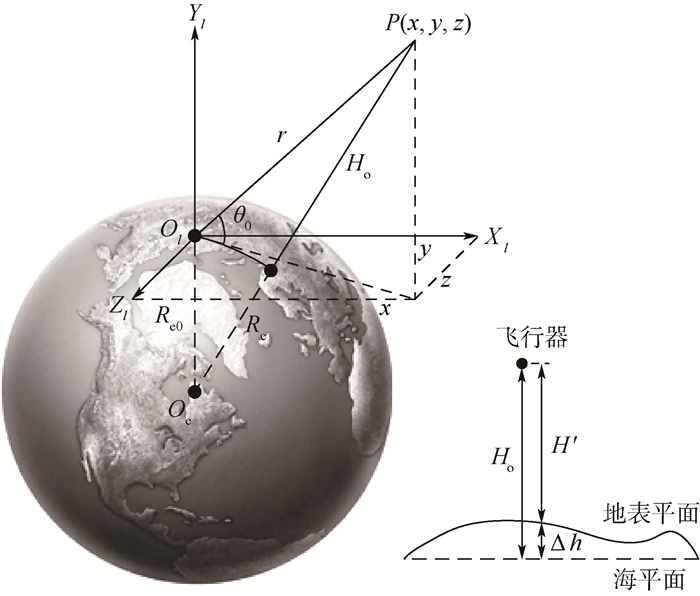 |
| 图 1 发射惯性系下雷达高度表测高示意图 Fig. 1 Geometric illustration of RA in launch inertial system |
| 图选项 |
在l系Ol-XlYlZl下,位置矢量
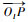
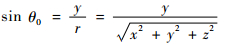 | (3) |
式中:r=
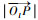
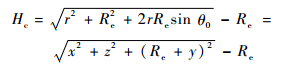 | (4) |
Hc与Ho之差ΔH满足如下关系:
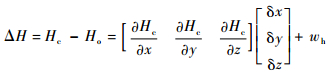 | (5) |
式中:
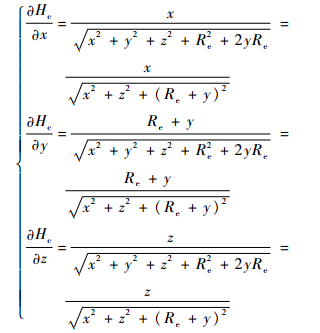 | (6) |
wh为误差项,受导航误差及量测噪声影响;δx、δy、δz分别为捷联解算与标称弹道的位置误差。
2 弹道环境分析 弹道导弹飞行过程一般分为主动段、中段与再入段。主动段由于发动机点火工作,导弹时刻处于大振动环境且质量变化较大;而再入段中,高速飞行的弹头将会受到强大气动力作用[11]。因此对于依赖相对静态环境的星敏感器而言,通常将中段作为工作段,此时空间气动力可以忽略,飞行稳定后三轴角速率较小[12]。由于中段约占全弹道的80%~90%,因此如何提高中段导弹的导航精度对于弹道导弹来说显得尤为重要[13]。在没有施加姿态机动的情况下,导弹飞行全过程如图 2所示。
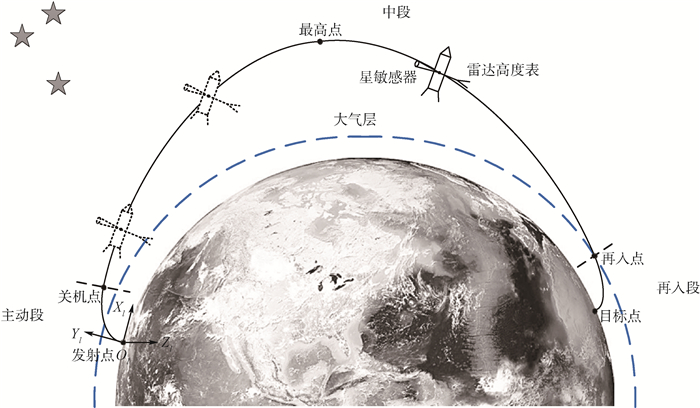 |
| 图 2 无姿控弹道示意图 Fig. 2 Schematic of ballistic trajectory without attitude control |
| 图选项 |
星敏感器通过星光成像并获得在成像阵列上星像质心位置,由星图识别及定姿算法,通过安装矩阵,可以获得导弹本体系(以下简称b系)相对地心赤道惯性坐标系(以下简称i系)下的实时姿态[14]。同时l系到i系的坐标转换矩阵Cli与发射时刻状态有关,其大小满足:
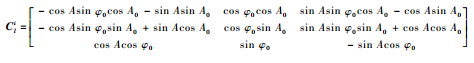 | (7) |
式中:A为发射时导弹相对于地理北向的发射方位角;A0=λ0+AΥ0,λ0、φ0为初始发射位置的地理经纬度,AΥ0为发射时刻春分点格林时角。进而得到b系相对l系的坐标转换矩阵
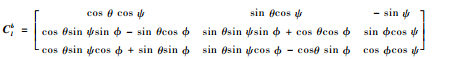 | (8) |
式中:?、ψ、θ为绝对姿态角。当弹体在真空环境中无角速率处于绝对静止状态时,Clb保持不变。
以导弹质心为坐标原点建立当地铅垂坐标系On-XnYnZn(即北-东-地坐标系,以下简称n系),进而得到b系相对n系的相对姿态角?r、ψr、θr,其坐标转换矩阵为
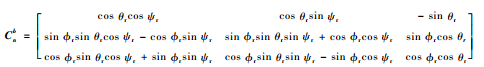 | (9) |
在n系下根据雷达高度表的捷联安装方式及相应测高算法对导弹进行实时姿态机动,以确保雷达有效测高[8]。
弹道导弹再入段飞行导航精度取决于地球坐标系(以下简称e系)。通过解算中段飞行位置的地理经纬度λ、φ,有利于导弹的实时导航与控制,从而实现末段精确制导。i系到e系的坐标转换矩阵为
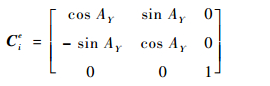 | (10) |
式中:AΥ伪前时刻春分点格林时角[15]。则由式(11)即可解算出当前λ、φ的计算主值:
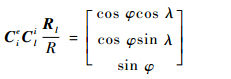 | (11) |
式中:Rl为
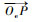
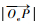
3 SINS/CNS/RA组合方案 3.1 总体方案 由捷联惯组获得解算绝对姿态角、当前位置地理经纬度及海拔计算高度,由星敏感器获得高精度绝对姿态信息用于补偿惯导陀螺漂移,由雷达高度表结合数字地图获得海拔观测高度用于校正定位误差,设计非线性扩展卡尔曼滤波器,建立SINS/CNS/RA组合导航新算法。整体方案流程图如图 3所示。
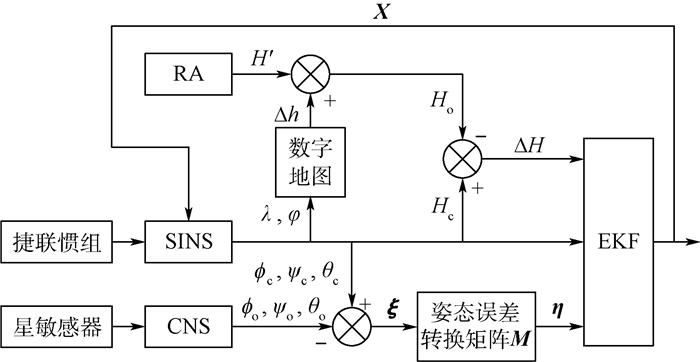 |
| 图 3 SINS/CNS/RA组合导航方案流程图 Fig. 3 Flowchart of SINS/CNS/RA integrated navigation scheme |
| 图选项 |
图中X为状态变量,?c、ψc、θc为捷联解算获得的姿态角,?o、ψo、θo为星敏感器观测获得的姿态角,ξ为绝对姿态误差角,η为数学平台失准角,且η=M×ξ[16]。
在姿态机动条件下,陀螺仪输出角速率ω由机动角速率ωm、陀螺漂移ε及随机噪声wg三部分构成,满足
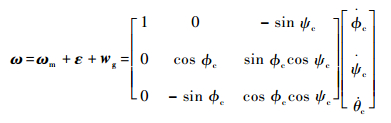 | (12) |
3.2 状态方程 以捷联惯导三轴数学平台失准角ηx、ηy、ηz,l系三轴速度误差δvx、δvy、δvz和位置误差δx、δy、δz,3个陀螺仪漂移εx、εy、εz和3个加速度计偏置?x、?y、?z建立15维状态变量:
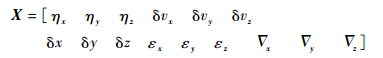 | (13) |
式中:陀螺漂移ε包含陀螺随机常值漂移εb和一阶马尔可夫过程εr,即ε=εb+εr;加速度计偏置?包含加速度计常值漂移?b和一阶马尔可夫过程?r,即?=?b+?r[17]。
考虑J2项引力摄动项的影响[6],摄动状态方程为
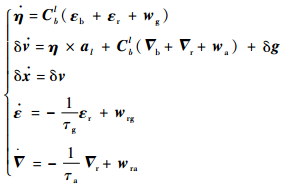 | (14) |
式中:al为加速度计所敏感的视加速度矢量在l系下的投影;wg、wa分别为陀螺仪及加速度计模型的高斯白噪声;v为速度;wrg、wra为对应一阶马尔可夫过程的驱动高斯白噪声;τg、τa为相关时间常数,当时间常数较大时一阶马尔可夫过程可近似为高斯白噪声;导航坐标系下重力加速度g满足
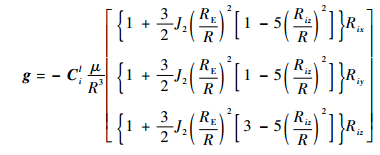 | (15) |
式中:μ为万有引力常数与地球质量的乘积;RE呜球赤道半径;Rix、Riy、Riz分别为
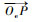
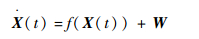 | (16) |
式中:W为系统噪声。
3.3 观测方程 构建4维系统观测量,包括由星敏感器与捷联惯导测得的ξ以及由雷达高度表测得的ΔH两部分,即
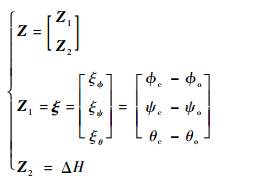 | (17) |
于是,观测方程为
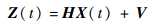 | (18) |
式中:
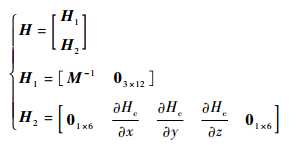 | (19) |
V=[V???Vψ??Vθ??wh]T为观测噪声。
3.4 EKF滤波设计 虽然捷联惯导严格意义上属于非线性系统,但为了简化模型便于研究,在姿态误差角为小量的条件下,采用卡尔曼滤波进行线性化处理,通常能够满足精度要求。不过,随着量测时间间隔的增加以及持续噪声的影响,SINS误差积累会导致系统非线性增强。同时由地球椭球模型所引起的重力加速度偏差也对系统摄动状态方程产生重要影响。鉴于此,本文采用EKF算法进行处理。
对于采样输出率高的惯导系统,其连续非线性状态方程近似泰勒展开并略去二阶以上项得
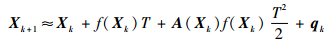 | (20) |
式中:Xk=X(tk)为k时刻状态变量;A(X)=
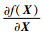
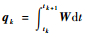
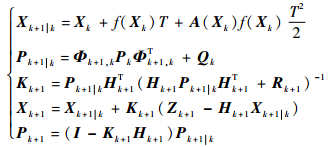 | (21) |
式中:Pk、Qk、Rk、Kk分别为k时刻卡尔曼滤波状态估计阵、系统噪声阵、观测噪声阵、增益矩阵;Φk+1, k=I+A(Xk)T为k时刻状态传递函数。
由于星敏感器与雷达高度表的采样周期不同,造成观测量Z1、Z2数据的采集不同步,因而采用集中式滤波结构,在不断对系统进行时间更新的基础上,适时间断进行局部量测更新。
4 实验仿真 4.1 仿真条件设置 为验证滤波算法,设计标称弹道轨迹发生器作为信息源,其仿真参数如下:
1) 发射点时刻t0(t0=0)
(φ0, λ0)=(40°N, 100°E),海拔高度10 m,方位角42°,AΥ0=0°。
2) 主动段(推力加速度at=40 m/s2)
① 垂直飞行段t0~t1(t1=10 s) θr=90°
② 程序飞行段t1~t2(t2=30 s)
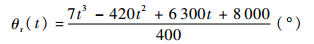 |
③ 瞄准飞行段t2~t3(t3=205 s) θr=20°
3) 中段(at=0)
① 无控调整段t3~t4(t4=250 s) θr ≈ 20°
② 姿态控制段
a.t4~t5(t5=400 s)
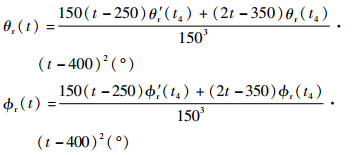 |
b.t5~t6(t6=1 810 s)
θr= 0°,?r=0°,弹道最高点海拔为1 017 km。
4) 再入点时刻t6
(φr, λr)=(40°6′36″ N, 129°1′45″ W),海拔高度为70 km,射程为9 828 km。
标称弹道轨迹曲线如图 4所示。
 |
| 图 4 标称弹道轨迹曲线 Fig. 4 Nominal ballistic trajectory curves |
| 图选项 |
t0时刻,位置误差5 m,速度误差0.1 m/s,方向失准角6′,水平失准角10″。导航器件精度如表 1所示,σ为误差标准差。
表 1 导航器件仿真参数 Table 1 Simulation parameters of navigational apparatus
| 导航器 | 精度 | 采样周期 | 工作阶段 |
| 陀螺仪 | 常值漂移0.5(°)/h | 0.01s | t0 ~ t6 |
| 随机漂移0.1(°)/h(1σ) | |||
| 加速度计 | 常值偏置50 μg | ||
| 随机误差10 μg(1σ) | |||
| 星敏感器 | 安装误差5″ | 0.1s (交替间隔0.05s) | t5 ~ t6 |
| 测量误差10″(1σ) | |||
| 雷达高度表 | 测量误差50m(1σ) |
表选项
4.2 仿真结果分析 在标称弹道上分别对SINS、SINS/CNS与SINS/CNS/RA进行仿真,结果如图 5和图 6所示。
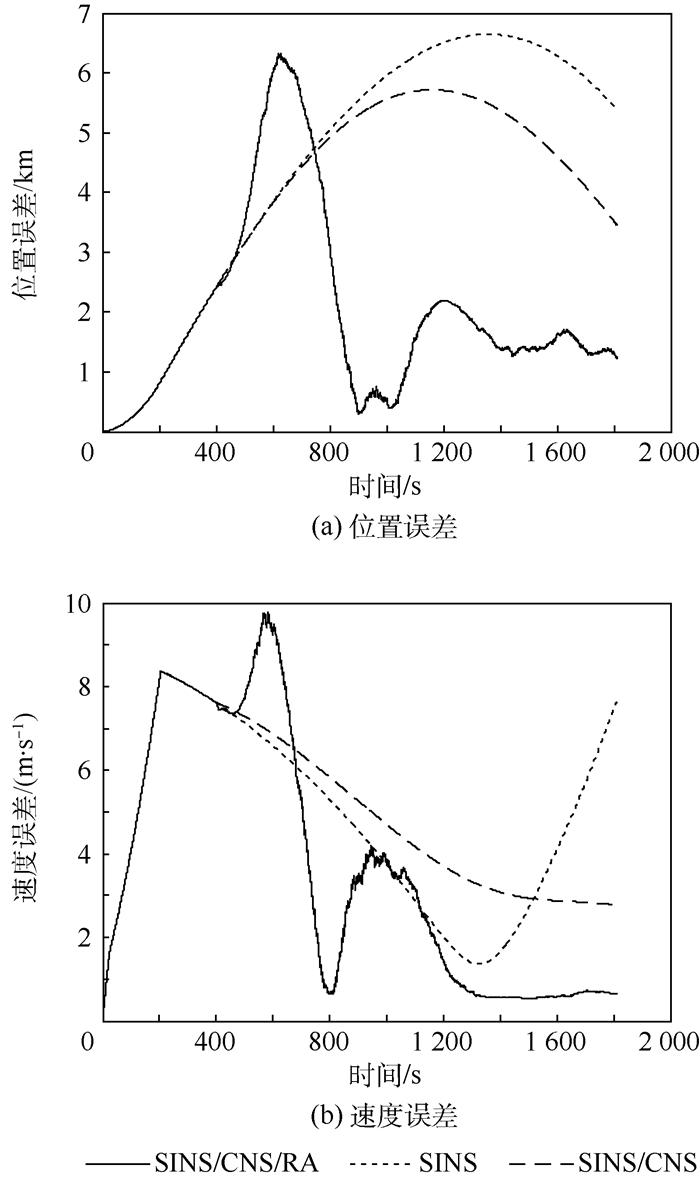 |
| 图 5 l系下位置、速度误差曲线 Fig. 5 Position and velocity error curves in l frame |
| 图选项 |
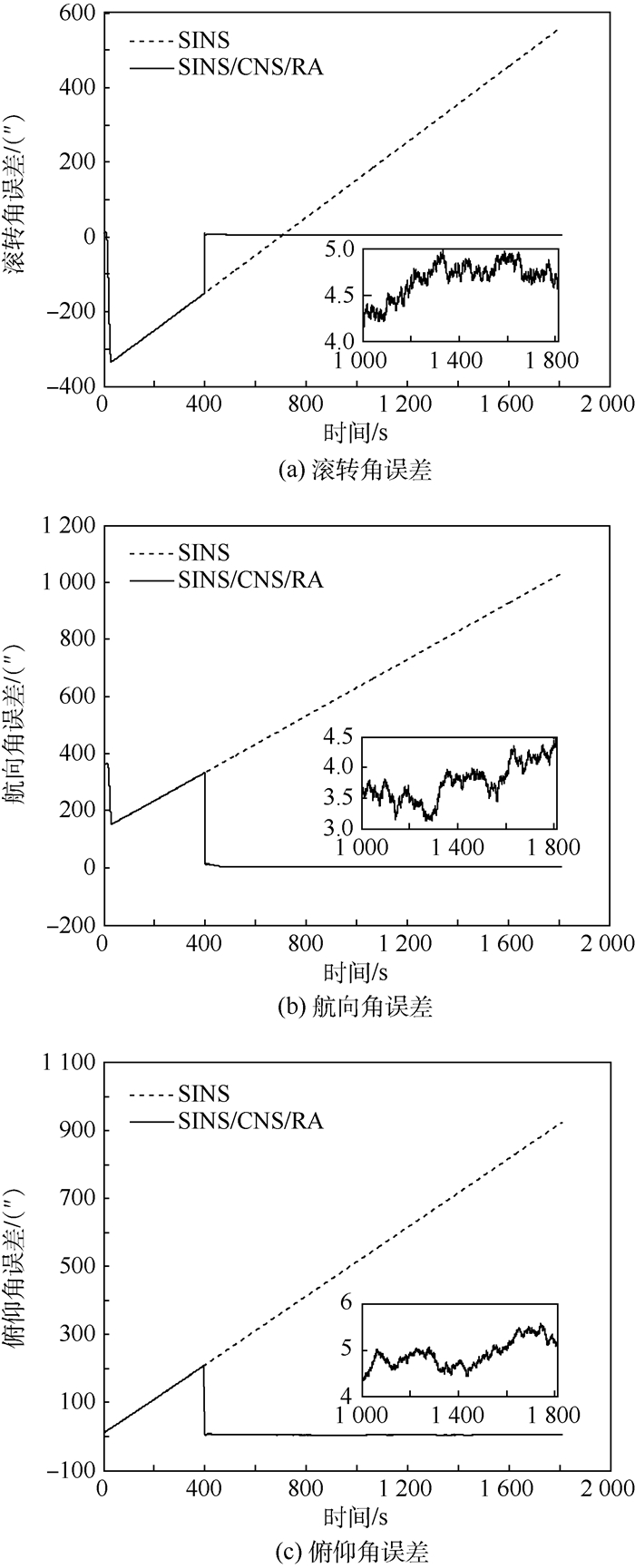 |
| 图 6 l系下姿态误差曲线 Fig. 6 Attitude error curves in l frame |
| 图选项 |
由图 5可以看出,受主动段影响导弹在关机点时刻已具有较大误差,经过1 810 s时间的飞行,当SINS单独工作时各项误差指标均明显发散;SINS/CNS组合后位置、速度误差发散得到抑制;SINS/CNS/RA组合后,通过一维位置信息的观测校正,经滤波处理,位置、速度误差趋于振荡收敛,导航位置、速度精度显著提高。如表 2所示。
表 2 再入点误差 Table 2 Reentry point error
| 组合模式 | 位置误差/m | 速度误差/(m·s-1) |
| SINS | 5 396 | 7.63 |
| SINS/CNS | 3 456 | 2.72 |
| SINS/CNS/RA | 1 211 | 0.65 |
表选项
由图 6可知,1 000 s后经滤波处理,SINS/CNS/RA组合姿态角误差分别减小为4.70″、3.83″、4.97″(RMS)。
为了更好验证雷达高度表在地心方向上的位置校正效果,对组合导航系统n系下各分量位置误差仿真图 7所示。
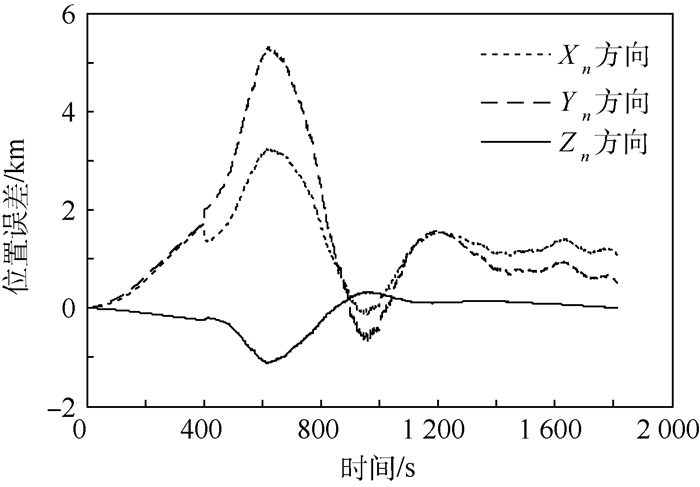 |
| 图 7 n系下位置误差曲线 Fig. 7 Position error curves in n frame |
| 图选项 |
在姿态机动的条件下,雷达高度表可实时获得Zn轴方向的观测信息,通过n系相对惯性系l系的坐标转换,经由滤波器耦合解算实现对导弹位置信息的校正。从图中可以看出,再入点位置处3轴定位误差分别为1 090、526、6 m,Zn轴方向的定位精度明显高于其他方向。
独立重复试验20次,统计用本方法得到的再入点估计位置相对标称位置的误差,计算圆概率误差(CEP)。结果如图 8、表 3所示。
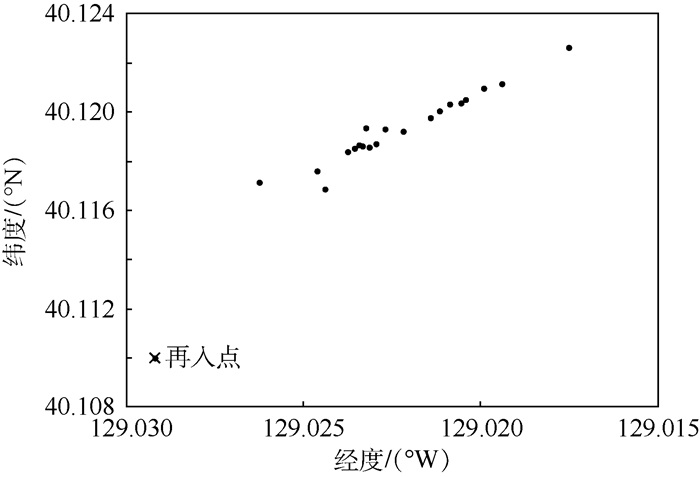 |
| 图 8 再入点位置分布统计图 Fig. 8 Cartogram of reentry point position distribution |
| 图选项 |
表 3 再入点位置误差统计表 Table 3 Statistics of reentry point position error
| 再入点坐标(φr, λr) | 位置误差/m |
| (40°7′7″ N, 129°1′23″ W) | 1 098 |
| (40°7′3″ N, 129°1′29″ W) | 942 |
| (40°7′9″ N, 129°1′22″ W) | 1 186 |
| (40°7′16″ N, 129°1′12″ W) | 1 472 |
| (40°7′7″ N, 129°1′24″ W) | 1 094 |
| (40°7′6″ N, 129°1′26″ W) | 1 056 |
| (40°7′11″ N, 129°1′17″ W) | 1 286 |
| (40°7′10″ N, 129°1′24″ W) | 1 172 |
| (40°7′7″ N, 129°1′24″ W) | 1 095 |
| (40°7′9″ N, 129°1′20″ W) | 1 200 |
| (40°7′21″ N, 129°1′3″ W) | 1 741 |
| (40°7′7″ N, 129°1′22″ W) | 1 119 |
| (40°7′14″ N, 129°1′15″ W) | 1 385 |
| (40°7′2″ N, 129°1′34″ W) | 845 |
| (40°7′7″ N, 129°1′25″ W) | 1 076 |
| (40°7′12″ N, 129°1′16″ W) | 1 325 |
| (40°7′1″ N, 129°1′28″ W) | 876 |
| (40°7′13″ N, 129°1′14″ W) | 1 385 |
| (40°7′14″ N, 129°1′13″ W) | 1 402 |
| (40°7′16″ N, 129°1′10″ W) | 1 511 |
表选项
由统计特性可以看出,惯导级精度捷联惯组经校正后再入点时刻位置误差保持在2 km以内,CEP为1.2 km。
5 结论 1) 本文方法能够确保导航系统高精度定姿,姿态误差分别为4.70″、3.83″、4.97″(RMS),趋近于星敏感器安装误差。
2) 在原有SINS/CNS两者组合的基础上引入高度测量信息,逐步校正了主动段造成的累积误差,提高了导航系统定位精度,使得速度、位置误差由原先的发散变为振荡收敛,再入点速度、位置误差分别减小了76.1%和65.0%。
考虑到弹体动态特性以及匹配地形图高度数据精度对系统测量和滤波精度的影响,本文采用精度为50 m(1σ)的雷达高度表测定高程,随着测量仪器精度的提高及测高算法的改进,最终定位精度仍有提升空间。
参考文献
| [1] | 徐帆, 房建成. 基于状态转移阵的SINS/星光组合速度位置误差估计方法[J].航天控制, 2007, 25(6): 27–31. XU F, FANG J C. Velocity and position error compensation using SINS/star integration based on evaluation of transition matrix[J].Aerospace Control, 2007, 25(6): 27–31.(in Chinese) |
| [2] | NING X L, WANG L H, BAI X B, et al. Autonomous satellite navigation using starlight refraction angle measurements[J].Advances in Space Research, 2013, 51(9): 1761–1772.DOI:10.1016/j.asr.2012.12.008 |
| [3] | QIAN H M, SUN L, CAI J N, et al. A starlight refraction scheme with single star sensor used in autonomous satellite navigation system[J].Acta Astronautica, 2014, 96: 45–52.DOI:10.1016/j.actaastro.2013.11.028 |
| [4] | 屈蔷, 刘建业, 熊智, 等. 机载天文/惯性位置组合导航[J].南京理工大学学报, 2010, 34(6): 729–732. QU Q, LIU J Y, XIONG Z, et al. Airborne SINS/CNS location integrated system[J].Journal of Nanjing University of Science and Technology, 2010, 34(6): 729–732.(in Chinese) |
| [5] | LORENZ R D, SVEDHEM H, TRAUTNER R, et al. Observations of the surface of Titan by the radar altimeters on the Huygens probe[J].Icarus, 2016, 270: 248–259.DOI:10.1016/j.icarus.2015.11.007 |
| [6] | 刘军, 韩潮. 基于UKF的雷达高度计自主定轨[J].北京航空航天大学学报, 2006, 32(8): 889–893. LIU J, HAN C. Autonomous orbit determination of spacecraft based on UKF using radar altimeter[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(8): 889–893.(in Chinese) |
| [7] | 邓欢, 李亚超, 全英汇, 等. 弹载下降段大前斜聚束SAR成像时序设计[J].系统工程与电子技术, 2016, 38(5): 1032–1038. DENG H, LI Y C, QUAN Y H, et al. Sequential design for highly squinted missile-borne spotlight SAR imaging on descent trajectory[J].Systems Engineering and Electronics, 2016, 38(5): 1032–1038.DOI:10.3969/j.issn.1001-506X.2016.05.10(in Chinese) |
| [8] | 张华. 雷达高度表动态环境模拟理论与技术研究[D]. 武汉: 华中科技大学, 2011. ZHANG H.Research on theory and technology of radar altimeter dynamic environment simulation[D].Wuhan:Huazhong University of Science and Technology, 2011(in Chinese).http://d.wanfangdata.com.cn/Thesis/D185961 |
| [9] | PATEL A, KWOK R, LEUSCHEN C, et al. Fine-resolution radar altimeter measurements on land and sea ice[J].IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2547–2564.DOI:10.1109/TGRS.2014.2361641 |
| [10] | 王海涌, 高自谦. 针对惯性导航的雷达高度表辅助方法: 201610180539. 9[P]. 2016-08-10. WANG H Y, GAO Z Q.Radar altimeter aided method based on inertial navigation:201610180539.9[P].2016-08-10(in Chinese).http://d.wanfangdata.com.cn/Periodical/htkz200706005 |
| [11] | 周啟航, 张刘, 霍明英, 等. 弹道导弹中段突防弹道设计与验证[J].光学精密工程, 2015, 23(9): 2645–2655. ZHOU Q H, ZHANG L, HUO M Y, et al. Design and validation of ballistic missile midcourse penetration trajectory[J].Optics and Precision Engineering, 2015, 23(9): 2645–2655.(in Chinese) |
| [12] | THEIL S, STEFFES S, SAMAAN M, et al.Hybrid navigation system for spaceplanes, launch and re-entry vehicles:AIAA-2009-7381[R].Reston:AIAA, 2009.http://arc.aiaa.org/doi/abs/10.2514/6.2009-7381 |
| [13] | 邓红, 刘光斌, 陈昊明, 等. 基于UKF的导弹SINS/CNS姿态估计方法[J].系统工程与电子技术, 2010, 32(9): 1987–1990. DENG H, LIU G B, CHEN H M, et al. Application of missile attitude estimation based on UKF algorithm[J].Systems Engineering and Electronics, 2010, 32(9): 1987–1990.(in Chinese) |
| [14] | ZHANG H B, ZHENG W, TANG G J. Stellar/inertial integrated guidance for responsive launch vehicles[J].Aerospace Science and Technology, 2012, 18(1): 35–41.DOI:10.1016/j.ast.2011.04.003 |
| [15] | SEIDELMANN P K, SEAGO J H. Time scales, their users, and leap seconds[J].Metrologia, 2011, 48(4): 186–194.DOI:10.1088/0026-1394/48/4/S09 |
| [16] | 李镇, 王海涌, 靳宇航, 等. 一种弹道导弹捷联惯导/地磁组合导航方法[J].中国惯性技术学报, 2015, 23(5): 636–641. LI Z, WANG H Y, JIN Y H, et al. Strapdown inertial/geomagnetic integrated navigation method for ballistic missile[J].Journal of Chinese Inertial Technology, 2015, 23(5): 636–641.(in Chinese) |
| [17] | LV P, LAI J Z, LIU J Y, et al. Stochastic error simulation method of fiber optic gyros based on performance indicators[J].Journal of the Franklin Institute, 2014, 351(3): 1501–1516.DOI:10.1016/j.jfranklin.2013.11.007 |
