双耦合Duffing振子仿真系统是一种比较新颖的检测方法,针对微弱信号的检测具有抗干扰能力较强、灵敏度高的特点。李月等[13]分析耦合参数的作用、大尺度周期相态时系统的复杂性以及系统各状态的比较,构造出一类含特定恢复力项双中强度耦合Duffing振子系统,并成功检测色噪声背景中的谐波、方波信号。吴勇峰等[14]研究环形耦合Duffing振子系统,成功演化出了耦合振子间的同步作用机理。杨东升等[15]提出一种针对未知频率微弱信号的分段测频检测方法,解决微弱信号检测的难点问题。利用双耦合Duffing振子系统有效解决了单Duffing振子微弱信号检测方法容易受到噪声影响干扰而产生误判这一问题。赵雪平等[16]通过对哈密顿系统和耗散系统进行仿真实验分析以及理论推导,证明在用于检测同相轴的Duffing型系统中,非线性恢复力项的选取至关重要。刘海波等[17]提出了一种新的微弱周期信号检测方法,即以Duffing振子系统相态由大周期态向混沌态的相变作为判据来检测信号,结果证明该方法在相变时受过渡带影响较小,具有较好的检测性能。
目前,两相流动特性的研究大都集中在常规管道和微米级通道,而介于2种尺度之间的毫米级小通道(尤其是1~5 mm)的研究成果相对匮乏,相关文献报道很少。基于上述原因,本文运用双耦合Duffing振子仿真系统,针对内径为2 mm×0.81 mm的矩形垂直玻璃通道内的气液两相流进行了流型动力学特性分析和研究。
1 理论基础 双耦合Duffing振子仿真系统方程如下:
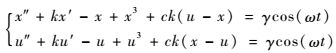 | (1) |
式中:c为耦合系数;k为阻尼比;(u-x)为耦合项;γcos(ωt)为系统周期策动力, γ为振幅, ω为角速度。当c=0时,系统的耦合现象消失,此时系统与单Duffing振子仿真系统的行为一样。当c≠0时,振子系统的2个变量x和u通过耦合作用逐渐趋于一致。另外,系统外加驱动力也令其具有相同的上述形式。MATLAB中的双耦合Duffing振子仿真系统如图 1所示。
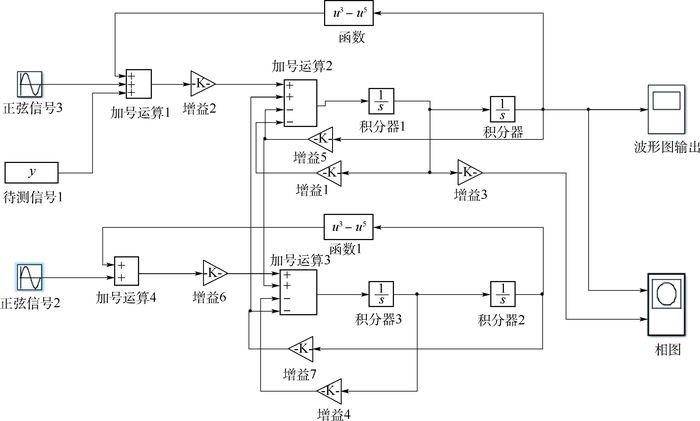 |
| 图 1 双耦合Duffing振子仿真系统 Fig. 1 Double coupled Duffing oscillator simulation system |
| 图选项 |
研究表明,相对于同一类振子仿真系统,双耦合振子仿真系统具有更复杂、精确的动力学特征。例如,利用耦合振子间存在的联系以及制约特点,获取到的相态更稳定,抗噪能力更强,这是单振子所不具有的。为了得到符合实验条件的双耦合Duffing振子仿真系统,将上述各参数输入系统运行,直到选取出仿真系统中较优的上述参数值。显然,这样有助于提高双耦合Duffing振子仿真系统的检测能力。
对于双耦合Duffing混沌振子仿真系统,本文采用了以下特定式:
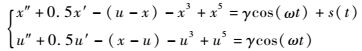 | (2) |
式中:耦合系数c=2;阻尼比k=0.5;内部策动力幅值γ=0.752 5;s(t)为待检测信号。为了能够较好地检测小通道气液两相流压降信号,本文选取ω=1 rad/s,相态边缘相对稳定,轨迹运动较活跃,易表征气液两相流流型作用机理。
对于双耦合Duffing振子仿真系统,当耦合作用出现并加强时,系统会产生一个频率相同的信号,该信号与系统信号振幅包络的同步调试有关,此类同步行为是振幅包络同步;强耦合Duffing振子之间的相差使耦合振子从混沌运动转变为周期运动;系统的耦合项还对相差具有抑制作用。根据双耦合Duffing振子方程式(2),利用MATLAB/Simulink软件建立仿真系统式(1)。
2 方法评价 为评价双耦合Duffing振子仿真系统处理被噪声污染的时间序列的有效性,本文从具有代表性的Lorenz和R?ssler混沌时间序列角度考察该方法在处理受到噪声污染的时间序列所表现出的抗噪性与表征能力。选择混沌时间序列作为评价本文方法的仿真信号,主要原因是考虑到现场所采集的信号具有典型的混沌特征,且混沌系统具有典型的动力学行为表征,具有一定的代表性。
2.1 混沌时间序列构建 对Lorenz以及R?ssler系统分别掺入不同程度噪声,组成几组时间序列,产生条件如下:
1) Lorenz混沌信号。Lorenz方程如下:
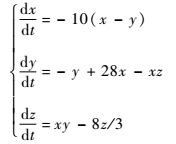 | (3) |
初始条件为:x=2, y=2, z=20, 运用四阶龙格-库塔迭代法,以变量x为仿真序列。
2) Lorenz+噪声。1)中所得变量x掺入5 dB高斯白噪声xx=awgn(x, 5)。awgn为MATLAB软件中的命令,awgn(x, 5)表示在x信号中加入信噪比为5 dB的高斯白噪声指令。
3) Lorenz+噪声。2)中所得变量xx与15 dB高斯白噪声直接掺混,yy=awgn(x, 5)+wgn(m, n, 15)。wgn同样为MATLAB软件中的命令,wgn(m, n, 15)表示生成一个m行n列的噪声强度为15 dBW的高斯白噪声序列。
4) R?ssler系统。
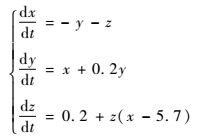 | (4) |
5) R?ssler+噪声。4)中所得变量x掺入5 dB高斯白噪声xx=awgn(x, 5)。
6) R?ssler+噪声。5)中所得变量xx与15 dB高斯白噪声直接掺混,yy=awgn(x, 5)+wgn(length(x), 15)。
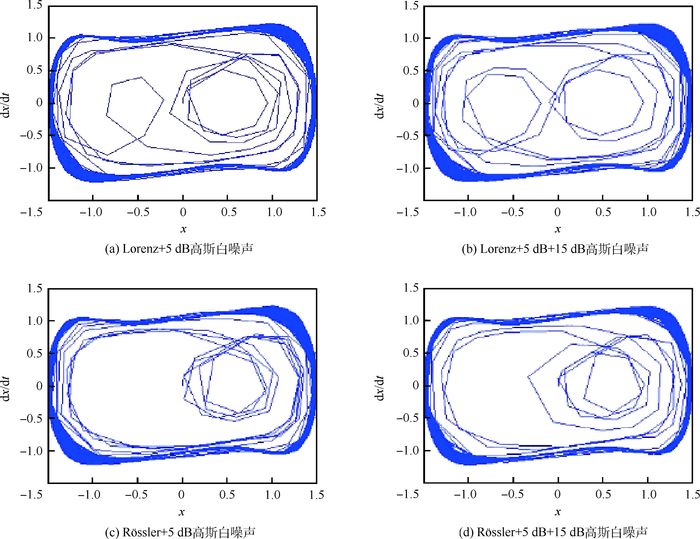
2.2 典型信号仿真验证 根据方程式(2),将待检测典型混沌信号Lorenz+5 dB高斯白噪声、Lorenz+5 dB+15 dB高斯白噪声、R?ssler+5 dB高斯白噪声、R?ssler+5 dB+15 dB高斯白噪声依次加入到双耦合Duffing振子仿真系统策动力中,其中阻尼比为0.5,耦合系数为2,若仿真系统由混沌态跃变到大尺度周期态,则表示有信号摄入,没有进入检测盲区[18-19],系统验证所得相图如图 2所示。图中:横轴代表振子位移,对应式(1)中的x;纵轴代表振子振动的瞬时速度,对应式(1)中的dx/dt。
 |
| 图 2 2种混沌信号不同噪声下的相轨迹图 Fig. 2 Phase trajectory chart of two chaotic signals with different noise |
| 图选项 |
混沌系统是敏感地依赖于初始条件的内在变化系统。典型混沌信号Lorenz、R?ssler在双耦合Duffing振子仿真系统中完成仿真,初始条件已经设定。从图 2中可知,随着噪声的增加,该环的边界变得粗糙,这些粗糙的摆动围绕着理想环往复振荡,且向外振荡幅度基本处于等幅振荡,向内振荡幅度按着某种规律不等幅振荡,混沌程度明显增大,相图变化完全反应了典型混沌信号Lorenz、R?ssler的混沌特征,相图轨迹随着噪声的增加,轨迹按一定规律变化,说明双耦合Duffing振子仿真系统能在一定的噪声环境下检测到更多的有效信息,有较好的抑制噪声作用。
通过以上2种典型混沌信号的验证,双耦合Duffing振子仿真系统可以检测混沌信号,充分显示其混沌特征,小通道气液两相流压降信号也具有周期、混沌、噪声的非线性波动信号特点,伴随着流型转变过程,其非线性特征极为突出,符合双耦合Duffing振子仿真系统检测信号的特点,说明应用该系统检测小通道气液两相流压差信号是可行的。同时,通过对混沌信号的验证,也证明了搭建的双耦合Duffing振子仿真系统的正确性。
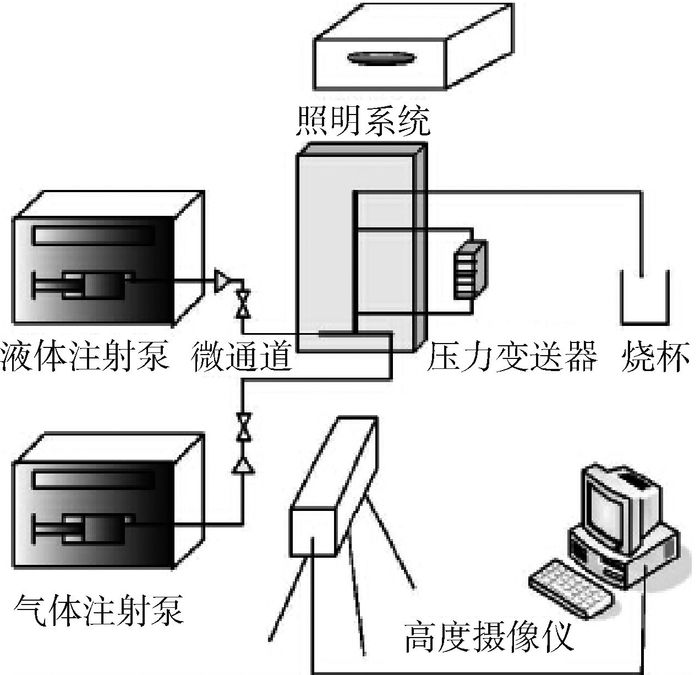
3 流型辨识及其动力学机理分析 如图 3所示,实验系统由气液两相流动与控制装置、数据采集装置等部分组成。实验段所采用的材料为透光性、可视性强的有机玻璃。在通道相距150 mm处分别选取2个直径为0.3 mm的测压圆孔,上游微孔距离通道入口80 mm,下游小孔距离通道出口60 mm,矩形微通道横截面宽为2.0 mm,缝隙为0.81 mm,水力直径为0.85 mm。
 |
| 图 3 气液两相流实验系统 Fig. 3 Gas-liquid two-phase flow experimental system |
| 图选项 |
实验环境压力取值为(0.1±0.000 5) MPa,实验环境所处温度为(25±0.5) ℃,气相表观速度jg为0.1~30 m/s,液相表观速度jL为0.01~5 m/s。
实验段上采集到4种典型流型的图像和差压信号,并利用双耦合Duffing振子仿真系统进行检测,结果如图 4~图 8所示。
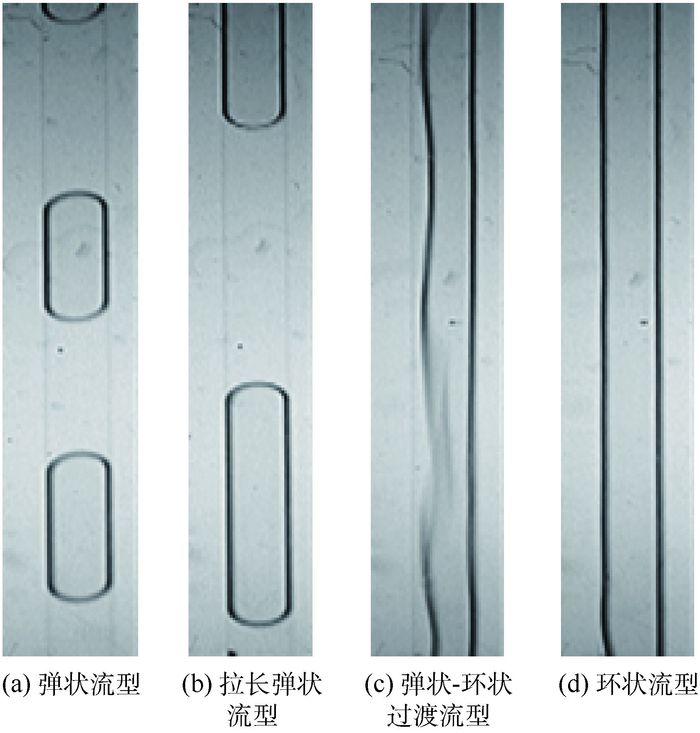 |
| 图 4 4种典型流型的图像 Fig. 4 Images of four typical flow patterns |
| 图选项 |
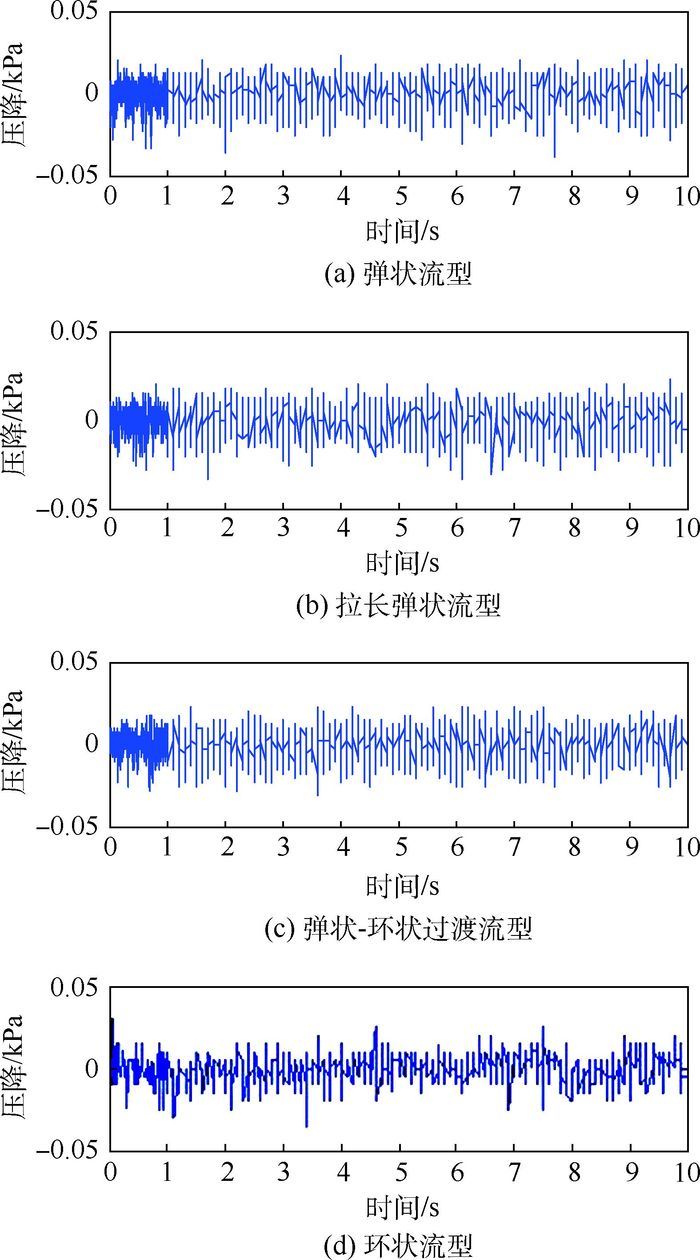 |
| 图 5 4种典型流型的差压信号 Fig. 5 Pressure difference signals of four typical flow patterns |
| 图选项 |
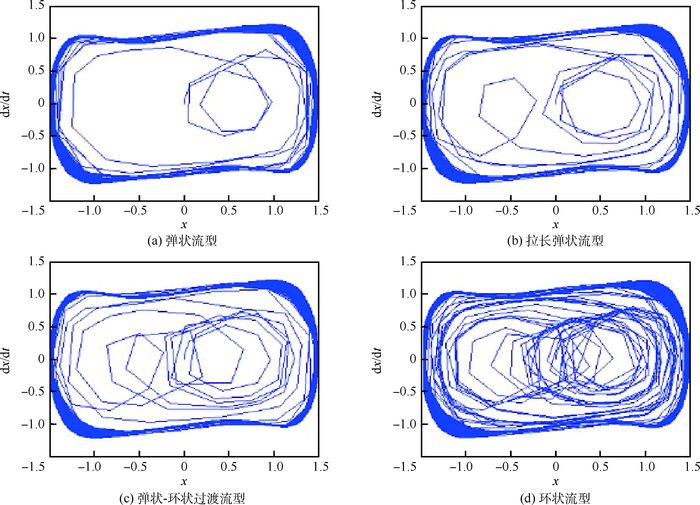 |
| 图 6 jL=0.277 8 m/s时4种典型流型对应的系统相图 Fig. 6 System phase diagrams of four typical flow patterns when jL=0.277 8 m/s |
| 图选项 |
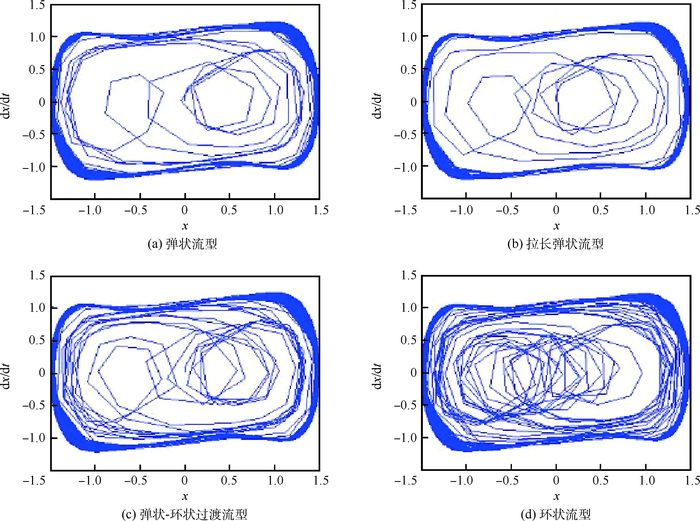 |
| 图 7 jL=0.694 5 m/s时4种典型流型对应的系统相图 Fig. 7 System phase diagrams of four typical flow patterns when jL=0.694 5 m/s |
| 图选项 |
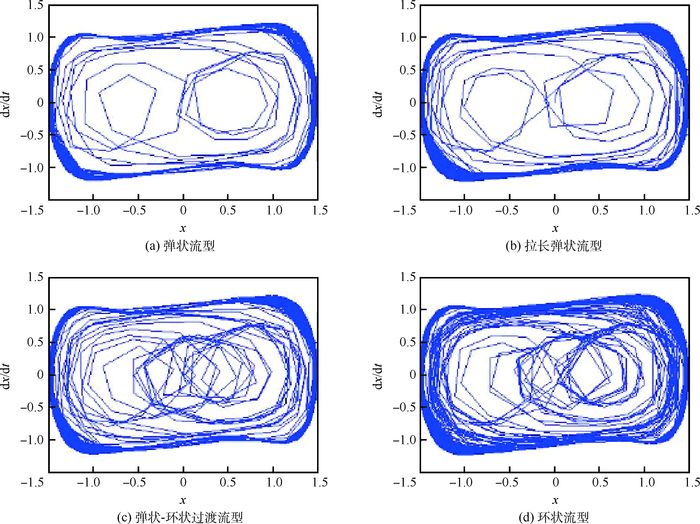 |
| 图 8 jL=1.389 0 m/s时4种典型流型对应的系统相图 Fig. 8 System phase diagrams of four typical flow patterns when jL=1.389 0 m/s |
| 图选项 |
图 6为液相表观速度为0.277 8 m/s时4种典型流型的系统相图。图 6(a)为小通道弹状流型,圆环内混沌程度不大,边缘较圆滑,说明该流型的周期性更好,流动结构相对简单;气相表观速度开始增大,气弹在拉长时呈现圆柱状,且气液间隔出现向下流动,如图 6(b)所示;气相表观速度继续增大,压力变大,混沌程度逐渐变得剧烈,气弹破碎,气液两相碰撞激烈,其状态如图 6(c)所示;当气相表观速度超过一定值时,液相连续地分布附着在管道周围,此时气相核心处于通道中心,呈线性流动,气液两相界面扰动加强,界面波动剧烈,混沌程度此时达到最大,出现典型的环状流型,如图 6(d)所示。图 7和图 8分别给出了液相表观速度为0.694 5、1.389 0 m/s时4种典型流型的系统相图。与图 6相比,随着液相表观速度的增大,小通道内气液两相流动速度明显加快,管内运动剧烈,相图中圆环内混沌程度增强,边缘环稳定性降低,但仍能表征4种典型流型特征的变化。可知,利用双耦合Duffing振子仿真系统检测,所受噪声污染小,检测到的有效信息相对多,有助于对小通道气液两相流动进行分析与推演。
为了定量地对气液两相流动力学特性进行分析,结合Duffing振子仿真系统,本文提取了振子振动的瞬时速度和位移2个特征值。其中,振子位移代表在系统策动力下振子发生相应的周期性位置变化,对应于式(2)中的x或u,振子振动瞬时速度是振子振动位移对时间项的求导,对应于式(2)中的dx/dt或du/dt。
从上述分析中可以看出,弹状流型和拉长弹状流型的系统相图形态相近,其流动机理都是气弹和液弹之间相互交替流动,气弹在流动中受到液弹的作用,处于弹状流型的工质随着气相速度增加,气弹变长,形成拉长弹状流型,流动形式未发生变化,故在提取特征值的讨论分析中,把弹状流型与拉长弹状流型统称为弹状流型加以分析。
图 9为液相表观速度为0.6945m/s时振子振动瞬时速度随气相表观速度的变化情况。在应用Duffing振子演化小通道气液两相流动过程中,振子振动瞬时速度表征压力衍生速度,在t=1 s时刻,处于流型转变的初始阶段,随着气相表观速度的增大,小通道内流动速度增大,气液两相不断发生碰撞,活动剧烈,压力衍生速度逐渐变大,振子振动瞬时速度也在不断增大;在t=5 s时刻,随着气相表观速度的继续增大,促使流型发生转变,其过程最为剧烈,压力衍生速度持续增大,振子振动瞬时速度依然增大;到达t=10 s时刻,振子振动瞬时速度随着气相表观速度的增大,较小幅度变大之后逐渐趋于平缓,相对于1s、5 s时刻振子振动瞬时速度增幅较大。这是因为管道内两相流动达到一个相对稳定的状态,流型变换波动相对减弱,压力衍生速度变化不大,在液相表观速度一定的情况下,由于形成环状流型的气相表观速度较大,则导致压力衍生速度较1 s、5 s时刻增幅较大,振子振动瞬时速度明显增大。此演化过程实际上反映出了小通道气液两相混合初始阶段、混合阶段、稳定阶段压力衍生速度的变化规律。
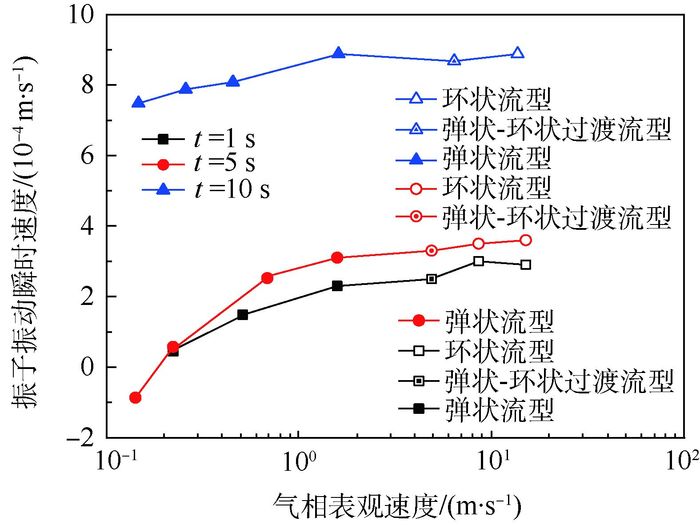 |
| 图 9 振子振动瞬时速度随气相表观速度的变化 Fig. 9 Variation of oscillation instantaneous velocity of oscillator with gaseous phase superficial velocity |
| 图选项 |
为了方便后面的流型分类讨论,先对不同时刻的振子振动瞬时速度对不同流型的表征程度进行了判断。选用2个指标来衡量分类效果[20]。
首先考虑2组数据间的比率因子:
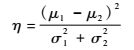 | (5) |
式中:μ1和μ2为统计2种不同流型序列参数的均值;σ1和σ2为相应的标准差。为获取一个好的分类,组间数据均值的平方差应远远大于其标准差,即η?1。其次,还要满足的是计算需达到2组数据最小不正确分类状态下边界均值的统计距离d2。
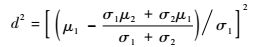 | (6) |
表 1列出了不同时刻振子振动瞬时速度的3种流型间的η和d2值。这2个值越大,表明本文方法的分类效果越明显。从表 1中可以明显看出,1 s时刻的振子振动瞬时速度对于3种流型的区分度更好,所以接下来本文针对1 s时刻对应的振子位移进行了进一步分析,并基于这2个参数进行了流型识别分析。
表 1 不同时刻振子振动瞬时速度在3种流型间的η和d2值 Table 1 Values of η and d2 of oscillation instantaneous velocity of oscillator among three flow patterns at different moments
| 时刻/s | ηs, sa | ηs, a | ηsa, a | ds, sa2 | ds, a2 | dsa, a2 |
| 1 | 2.524 | 3.047 | 2.986 | 1.124 | 1.397 | 0.985 |
| 5 | 1.875 | 2.892 | 1.203 | 1.254 | 1.048 | 0.532 |
| 10 | 2.305 | 1.907 | 2.387 | 0.856 | 1.113 | 1.065 |
| ????注:s—段塞流;a—环状流;sa—段塞-环状过渡流。 | ||||||
表选项
图 10为振子振动位移随气相表观速度变化的曲线。3条曲线的轨迹大致相似,随着气相、液相表观速度的增大,振子振动位移不断增大。根据双耦合Duffing振子方程式(2)及仿真系统特点,振子振动位移反映的是小通道气液两相流两点压差的大小,随着气相表观速度的增大,流型由弹状流型到弹状-环状过渡流型,弹状-环状过渡流型到环状流型变化,流量变大,单位时间内流过管道的工质增加,进而流体的动能增大,使其摩擦压降不断变大。
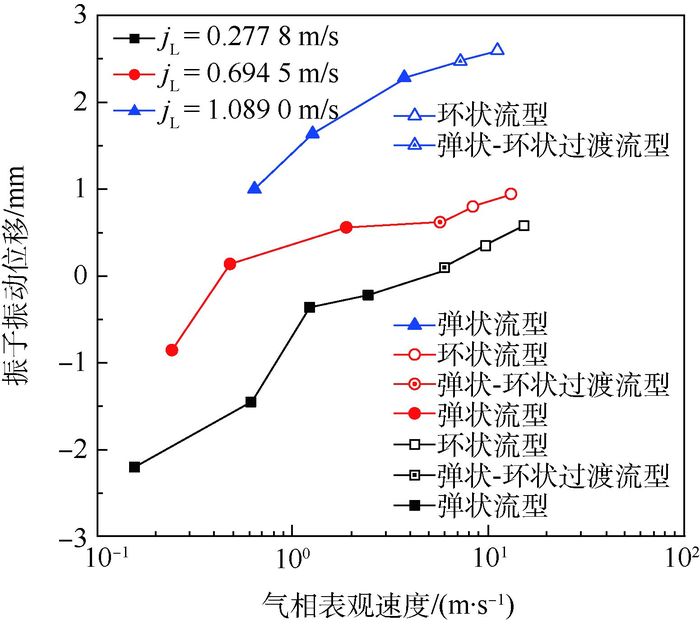 |
| 图 10 1 s时刻振子振动位移随气相表观速度的变化 Fig. 10 Variation of oscillation displacement of oscillator with gaseous phase superficial velocity at moment of 1 s |
| 图选项 |
通过双耦合Duffing振子仿真系统,利用1 s时刻振子振动瞬时速度结合振子振动位移的变化对流型进行辨识。为使识别结果更加具有代表性,本文对振子振动瞬时速度和位移做了无量纲处理,即分别将振子振动瞬时速度和位移除以平均振子振动瞬时速度和位移,也就是通过信号压力衍生速度这个无量纲物理表征量与信号的压降变化大小建立起联系,识别结果如图 11所示。
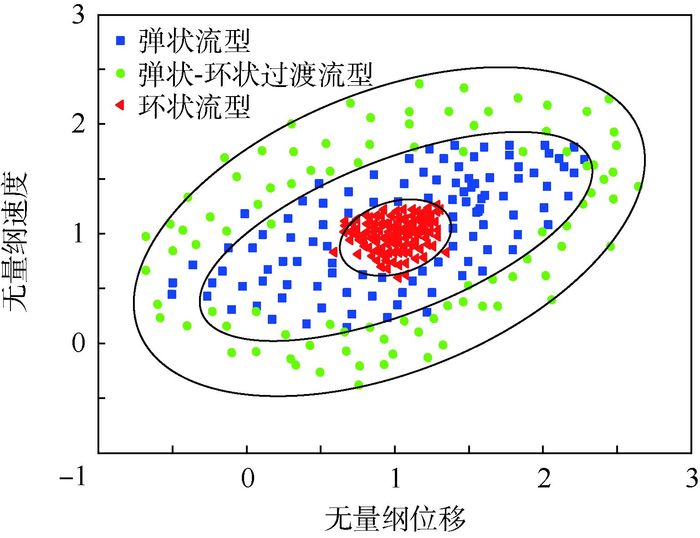 |
| 图 11 水力直径为0.85 mm时无量纲速度与位移的流型 Fig. 11 Flow pattern of dimensionless flow velocity and displacement when hydraulic diameter is 0.85 mm |
| 图选项 |
图 11为利用无量纲位移和速度对本实验中记录的3种流型所绘制的流型。可以看出,弹状流型、弹状-环状过渡流型、环状流型有明显的分隔线,其中环状流型处在图正中间位置,无量纲位移和速度都分布在数值1附近,这表明环状流型流动状态稳定,在流动过程中液相工质在管壁附近形成液膜,气相工质在液膜中间流过,随着工质表观速度的改变,其流动过程中产生的压降较小,流动压力和由此产生的压力衍生速度变化不大,趋于稳定。弹状流型无量纲位移处在-0.3~0.5与1.3~2.3之间,无量纲速度处在0~1.5之间。可见,系统在对弹状流型仿真分析时,振子振动瞬时速度和位移波动较大,这是由于弹状流型气相和液相交替流过管内,且随着工质速度的增加,气弹的长度在增加,对管中压力产生较大影响,使得压力波动较为明显,由此产生的压力衍生速度波动也随之增加。弹状-环状过渡流型是一种不稳定的流型,随着工质速度的增加,管内气弹长度变长且相邻2个气弹之间的距离越来越小,当二者相互接触时,气弹首尾端液膜破碎相互融合形成较大的气弹,此时在气弹接口处会产生小漩涡使液膜变薄,同时使得管内压力变化剧烈,系统中振子振动振幅较大且不稳定,压力衍生速度变化明显。
为了验证本文方法对小通道气液两相流动特性分析的普遍性,选取本课题组内水力直径为1.15 mm小通道[20]的压力信号进行特征参数提取,所得流型如图 12所示。结果表明,对于3种典型流型以无量纲振子速度与位移进行流型区域划分有明显的分隔线,对流型识别结果较好。
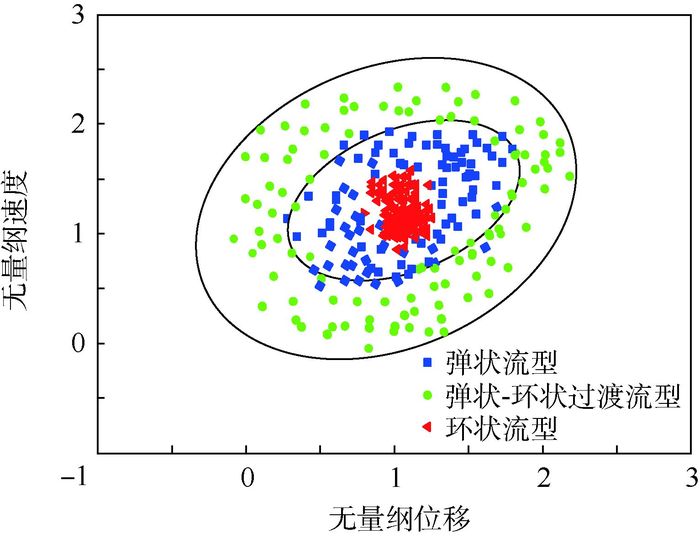 |
| 图 12 水力直径为1.15 mm时无量纲速度与位移的流型 Fig. 12 Flow pattern of dimensionless flow velocity and displacement when hydraulic diameter is 1.15 mm |
| 图选项 |
在应用本文方法对小通道气液两相流动特性分析时,进行特征参数分析未涉及有关尺寸的问题及参数,也即说明所得到的结论与通道尺寸无关,进而理论上说明本文方法可使用于常规管道及微小通道两相流的研究工作中。
4 结论 1) 本文提出了一种基于双耦合Duffing振子仿真系统检测小通道两相流信号的方法,同时应用2种典型混沌信号来验证该方法的正确性,主要是通过对抗噪能力与其对非线性的表征能力进行检测验证。实验结果表明,该方法在检测2种混沌信号时表现出较强的抗噪能力,能够很好地表征混沌信号的混沌特性。
2) 小通道气液两相流差压信号检测中,本文方法分析得到的流型区分度比较明显,而且振荡程度揭示出不同流型的流动机理,弹状流型由于明显的周期性使得振子在边环作等幅振荡,内部简单明了;在弹状流型转变为环状流型过程中,振子振荡随着气相表观速度的增大而剧烈,内部混沌明显加剧;环状流型较弹状流型与弹状-环状过渡流型更为复杂,其气相与液膜相互作用显示出强烈混沌特征。
3) 通过流型差压信号所得相图提取了振子振动瞬时速度、位移2个特征值,实现了对流型转变过程的非线性分析及3种流型的准确识别,发现无量纲振子振动瞬时速度与位移的组合能够很好地对流型进行分类。更进一步,将研究领域拓展到其他多相流的流型识别中,亦是有益的探究与尝试。
参考文献
| [1] | 杨亮, 丁国良, 黄冬平, 等. 超临界二氧化碳流动和换热研究进展[J].制冷学报, 2003(2): 51–56. YANG L, DING G L, HUANG D P, et al. Review of flow and heat transfer of supercritical carbon dioxide[J].Journal of Refrigeration, 2003(2): 51–56.(in Chinese) |
| [2] | 陈光文, 袁权. 微化工技术[J].化工学报, 2003, 54(4): 427–439. CHEN G W, YUAN Q. Micro-chemical technology[J].Journal of Chemical Industry and Engineering, 2003, 54(4): 427–439.(in Chinese) |
| [3] | 施丽莲, 蔡晋辉, 周泽魁. 基于图像处理的气液两相流流型识别[J].浙江大学学报, 2005, 54(4): 1128–1129. SHI L L, CAI J H, ZHOU Z K. Flow pattern identification of gas-liquid two-phase flow based on image processing[J].Journal of Zhejiang University, 2005, 54(4): 1128–1129.(in Chinese) |
| [4] | SUN B, WANG E P, DING Y, et al. Time-frequency signal processing for gas-liquid two-phase flow through a horizontal venturi based on adaptive optimal-kernel theory[J].Chinese Journal of Mechanical Engineering, 2011, 19(2): 243–252. |
| [5] | 黄竹清. 基于小波分析的垂直上升管气液两相流流型识别[J].中国电机工程学报, 2006, 26(1): 26–29. HUANG Z Q. Flow pattern identification of gas-liquid two-phase flow in vertical upward pipe based on based wavelet analysis[J].Proceedings of the CSEE, 2006, 26(1): 26–29.(in Chinese) |
| [6] | DU M, JIN N D, GAO Z K. Analysis of total energy and time-frequency entropy of gas-liquid two-phase flow pattern[J].Chemical Engineering Science, 2012, 82: 144–158.DOI:10.1016/j.ces.2012.07.028 |
| [7] | 金宁德, 陈万鹏. 混沌递归分析在油水两相流流型识别中的应用[J].化工学报, 2006, 57(2): 274–280. JIN N D, CHEN W P. Application of chaotic recursive analysis in flow pattern identification oil-water two-p-hase flow[J].Journal of Chemical Industry and Engin-eering, 2006, 57(2): 274–280.(in Chinese) |
| [8] | 李洪伟, 周云龙, 王世勇, 等. 小通道氮气水两相流三谱切片波动特性及其流型表征[J].物理学报, 2013, 62(14): 14050501–14050510. LI H W, ZHOU Y L, WANG S Y, et al. The sliced trispectrum fluctuation characteristics and flow pattern representation of the nitrtrogen-water two-phase flow of small channel[J].Chinese Journal of Physics, 2013, 62(14): 14050501–14050510.(in Chinese) |
| [9] | 李洪伟, 周云龙, 任素龙. 符号动力学信息熵在气液两相流型电导信号分析中的应用[J].化工学报, 2012, 63(11): 3486–3492. LI H W, ZHOU Y L, REN S L. Application of conductance signals analysis of gas-liquid two-phase flow patterns based on symbolic dynamics entropy[J].Journal of Chemical Industry and Engineering, 2012, 63(11): 3486–3492.DOI:10.3969/j.issn.0438-1157.2012.11.015(in Chinese) |
| [10] | 李洪伟, 周云龙, 刘旭, 等. 基于随机子空间结合稳定图的气液两相流型分析[J].物理学报, 2012, 61(3): 03050801–03050808. LI H W, ZHOU Y L, LIU X, et al. Stochastic subspace parameter identification and stability diagram of gas-liquid two-phase flow patterns[J].Acta Physica Sinica, 2012, 61(3): 03050801–03050808.(in Chinese) |
| [11] | LI H W, ZHOU Y L, HOU Y D, et al. Flow pattern map and time-frequency spectrum characteristics of nitrogen-water two-phase flow in small vertical upward noncircular channels[J].Experimental Thermal and Fluid Science, 2014, 54: 47–60.DOI:10.1016/j.expthermflusci.2014.01.017 |
| [12] | GAO Z K, JIN N D. Flow pattern identification and nonlinear dynamics of gas-liquid two-phase flow in complex networks[J].Physical Review E, 2009, 79(6): 066303.DOI:10.1103/PhysRevE.79.066303 |
| [13] | 李月, 杨宝俊, 赵雪平, 等. 检测地震勘探微弱同相轴的混沌振子算法[J].地球物理学报, 2005, 48(6): 1428–1433. LI Y, YANG B J, ZHAO X P, et al. An algorithm of chaotic vibrator to detect weak events in seismic prospecting records[J].Chinese Journal of Geophysics, 2005, 48(6): 1428–1433.(in Chinese) |
| [14] | 吴勇峰, 张世平, 孙金玮, 等. 环形耦合Duffing振子间的同步突变[J].物理学报, 2011, 60(2): 135–140. WU Y F, ZHANG S P, SUN J W, et al. Abrupt change of synchronization of ring coupled Duffing oscillator[J].Acta Physica Sinica, 2011, 60(2): 135–140.(in Chinese) |
| [15] | 杨东升, 李乐, 杨珺, 等. 基于双耦合混沌振子的未知频率弱信号检测[J].东北大学学报(自然科学版), 2012, 33(9): 1226–1230. YANG D S, LI L, YANG J, et al. Detection of the weak signal with unknown frequency based on the coupled chaos oscillator[J].Journal of Northeastern University(Natural Science), 2012, 33(9): 1226–1230.(in Chinese) |
| [16] | 赵雪平, 李月, 杨宝俊. 用于检测同相轴的Duffing型系统恢复力项的讨论[J].地球物理学进展, 2006, 21(1): 61–69. ZHAO X P, LI Y, YANG B J. The discussion to the resilience items in the Duffing type system used for detecting events[J].Progress in Geophysics, 2006, 21(1): 61–69.(in Chinese) |
| [17] | 刘海波, 吴德伟, 金伟, 等. Duffing振子微弱信号检测方法研究[J].物理学报, 2013, 62(5): 050501. LIU H B, WU D W, JIN W, et al. Study on weak signal detection method with Duffing oscillators[J].Acta Physica Sinica, 2013, 62(5): 050501.(in Chinese) |
| [18] | 牛德智, 陈长兴, 班斐, 等. Duffing振子微弱信号检测盲区消除及检测统计量构造[J].物理学报, 2015, 64(6): 060503. NIU D Z, CHEN C X, BAN F, et al. Blind angle elimination method in weak signal detection with Duffing oscillator and construction of detection statistics[J].Acta Physica Sinica, 2015, 64(6): 060503.(in Chinese) |
| [19] | AMARAL L A N, GOLDBERGER A L, IVANOV P C, et al. Scale-independent measures and pathologic cardiac dynamics[J].Physical Review Letters, 1998, 81(11): 2388–2391.DOI:10.1103/PhysRevLett.81.2388 |
| [20] | 周云龙, 王洪波. 矩形小通道内气液两相流垂直向上流动特性[J].化工学报, 2003, 62(5): 1226–1232. ZHOU Y L, WANG H B. Flow characteristics of gas-liquid two-phase flow in small vertical rectangular channel[J].Journal of Chemical Industry and Engineering, 2003, 62(5): 1226–1232.(in Chinese) |
