电容层析成像(Electrical Capacitance Tomography,ECT)技术[1]基于电容敏感机理在线监测被测物场中介电常数分布,具有响应速度快、非侵入、结构简单、成本低等优点[2]。在飞机复合材料缺陷可视化检测及航空发动机气路监测方面具有较好的应用潜力,目前已有****开展了相关的研究工作[3-4]。
按是否需要迭代,ECT的图像重建算法可以分为非迭代及迭代算法[5]。对于前者而言,如线性反投影算法,其优点为成像速度快,缺点为重建图像的质量差;而后者,典型的如Landweber迭代算法,虽然其重建图像的精度有所提高,但所需的迭代次数较多、速度慢。
Donoho于2006年基于稀疏分解及逼近论提出了压缩感知(Compressed Sensing,CS)的理论框架[6],该理论核心思想是:若原始信号本身具有稀疏性或可压缩性[7],那么可以采用随机观测的方式对原始信号进行低维投影,从而获得更少的采样信号。这种低维随机投影可保留原始信号绝大多数特征信息,使得原始信号可从少量投影信号中精确重建。CS理论突破了传统采样定理对采样带宽的限制,极大地减轻了信号采集系统和数据处理系统的负担,提高信号处理效率,为信号采集技术开启了新的篇章。目前,CS理论的研究已涉及军事、医疗、工业、社会生活等诸多领域[8]。
有许多****研究了采用稀疏性作为正则化约束的图像重建方法。张玲玲等研究了基于1范数的电阻层析成像图像重建算法[9],常甜甜等研究了基于CS的电阻抗图像重建算法[10],王丕涛等引入l1范数同时作为数据项和正则化项,将问题转化为凸优化问题,采用原始-对偶内插点法进行数值计算[11],Ye等提出基于稀疏表达的ECT图像重建算法[12]。
本文研究将CS理论应用于ECT图像重建中,利用CS可在低维采样同时实现高精度信号重建的优势,解决ECT系统成像欠定性问题。首先,使用快速傅里叶变换(Fast Fourier Transformation, FFT)基将原始图像灰度信号进行稀疏化处理;接着,将ECT灵敏度矩阵的各行按随机顺序进行排列,得到ECT系统随机观测矩阵;最后,使用多种当前流行的CS图像重建算法进行ECT图像重建,给出仿真结果。通过分析各种典型流型仿真结果,对各种CS图像重建算法优缺点及适用范围进行探讨。
1 压缩感知的基本理论 1.1 稀疏表示概述 若x为一离散信号,为N×1维列向量。则在RN空间中任选一组N×1维基向量{ψi}i=1N,均可将信号x作线性表示
 | (1) |
式中:Ψ为N×N维正交基,ΨN×N=[ψ1 ψ2 … ψN];s为N×1维的稀疏系数向量。s具有K(K?N)个非零系数,称为其稀疏度,Ψ则称为x的稀疏基,可依据信号自身的特点灵活选择[13]。
1.2 信号非相关测量 信号的线性测量为CS理论的核心技术,即用一个与稀疏基Ψ不相关的M×N(M < N)的测量矩阵Φ,对信号x进行线性投影,得到低维投影信号y,即
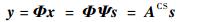 | (2) |
式中:ACS=ΦΨ为传感矩阵。
由式(2)可知,给定y,并从式(2)中求解x为线性规划问题,由于M < N,其为一欠定方程,因此无确定解。
若Ψ与Φ不相关,则在很大程度上可以保证有限等距限制性质(Restricted Isometry Property, RIP)[14],可以通过CS理论,从其M个测量值中对s的K个非零系数求解,实现信号x的精确重建。文献[15]指出,如果观测矩阵Φ和稀疏基Ψ不相关,ACS可在较高概率下满足RIP条件,从而可求解欠定方程式(2)。文献[16]证明,高斯随机矩阵与大多数固定的正交基矩阵不相关,可将其选作系统观测矩阵。
1.3 图像重建算法 最直接的方法是通过求解L0范数下的最优化问题来进行CS信号重构,即
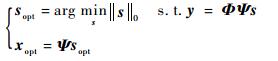 | (3) |
由于式(3)的求解是个NP难问题[17]。为求解该CS问题,研究者们先后提出了替代模型及其相应的CS重建算法。
1.3.1 内点法 Chen等指出[18],当Φ和Ψ不相关时,最小L1范数和最小L0范数具有相同的解。采用L1范数度量向量s的稀疏度,可使非凸问题式(3)转变为凸问题式(4),从而求解CS问题。
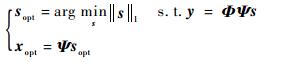 | (4) |
迄今为止,内点法是求解式(4)的精度最高的重建算法,其由加州理工的CS研究组[19]提出。由于L1最小范数与L0最小范数在一定条件下具有等价性,式(4)转化为式(5)所示的L1最小范数最优化问题,α为正则化参数。
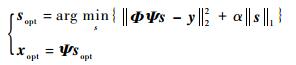 | (5) |
1.3.2 GPSR算法 梯度投影(Gradient Projection for Sparse Reconstruction, GPSR)算法[20]按正负将s分为两部分(u=(s)+=max(0, s>)≥0,v=(-s)+≥0,且有s=u-v),将式(6)的L1范数正则化模型转化为式(7)的二次规划问题,从而进行求解。
 | (6) |
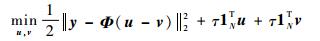 | (7) |
式中:τ为拉格朗日因子;1N为包含N个1的列向量。
1.3.3 贪婪算法 贪婪算法[21]的基本思想是采用迭代的方式在测量向量集合Φ中依次找出构成y的K个非零系数向量,基于某种贪婪准则,每次迭代找出一个或多个支撑向量,尽最大可能减少y与ΦΨs之间的能量残差。典型算法如正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[22],并采用如下模型求解:
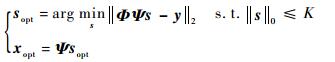 | (8) |
贪婪算法迭代次数严格依赖先验稀疏度K,具有迭代次数少,计算复杂度低,信号重建速度快等优点,其缺点是重建精度难以保证。
2 基于CS理论的ECT图像重建 对于管道内的两相流体,其截面图像为二值图像。欲将CS理论运用于ECT图像重建,必须将二值图像灰度信号稀疏化处理,使其满足CS前提条件。对常见两相流流型,经对比分析可得:FFT基可将多种典型流型的二值图像信号较好地进行稀疏化处理[23],稀疏向量s的稀疏度可达25~35。故可将其用作ECT系统稀疏基,对二值图像灰度信号稀疏化处理
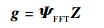 | (9) |
式中:g为N×1维重建图像灰度向量;ΨFFT为N×N维FFT基;Z为N×1维稀疏系数向量。
ECT系统的线性模型如下[1]:
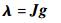 | (10) |
将式(9)代入式(10)中,得到
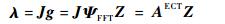 | (1) |
式中:J为M×N维灵敏度系数矩阵;AECT为ECT系统的传感矩阵;λ为M×1维的归一化观测投影向量。
典型16电极ECT系统独立测量数M=C162=16×15/2=120[1],管道内部成像区域采用正方形网格剖分,像素数N=812,即M?N,式(9)为欠定性方程,通常无确定解。结合CS理论,引入图像灰度信号可被稀疏处理的先验条件,则式(9)可以得到求解。
由CS理论可知:当观测矩阵为高斯随机矩阵[12]时,CS矩阵AECT满足RIP条件,稀疏向量Z的K个非零系数可由λ的M个独立测量值精确重建。由于ECT数据采集系统采用固定的激励测量方式,本文通过对J进行高斯随机重新排列,使AECT在一定概率下满足RIP条件。
具体做法如下:J的每一行代表一个角度的观测投影数据,按高斯随机将各行顺序打乱,产生了随机观测矩阵Jnew,与此相应的测量电容向量λ各行亦需以相同的顺序重新排列,获得相应的随机投影向量λnew。由此所得随机观测矩阵Jnew与稀疏基ΨFFT在一定程度上是不相关的,AECT在一定概率下可满足RIP条件,由此得到基于CS理论的ECT数学模型为
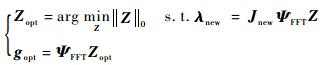 | (12) |
ECT图像重建过程即为模型式(12)的求解过程,其为典型的最小L0范数模型,可由1.3节所述的3类典型的CS图像重建算法求解。
重建图像灰度值g∈[0, 1],非二值图像,若寻找合适的阈值,进行图像的二值化处理,可使重建图像与原始图像更加接近。
本文使用最优阈值方法,考虑所有可能的阈值,然后由经过阈值处理后的重建图像计算出测量电容值,并计算其与实际测量电容值的误差,最终选取电容误差最小时所对应的灰度阈值为最优阈值,如式(13)所示:
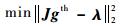 | (13) |
式中:gth为阈值处理后的图像灰度值。
3 仿真实验与结果分析 为研究CS理论在ECT系统图像重建中的应用效果,本文采用第1节所述的基于CS理论的内点法、GPSR算法和OMP算法,选择了5组模型,分别进行图像重建,并与采用LBP算法及Landweber迭代算法所得的重建图像进行比较,以分析基于CS理论的ECT图像重建算法的重建效果。
本文以油气两相流为仿真对象,进行无量纲仿真,管道半径为1,管壁厚度0.1,16电极ECT传感器,电极张角为18°,设定5种典型流型进行仿真,其中流型1和流型2考察重建算法对于简单流型的重建效果,流型3和流型4考察对于复杂流型的重建效果,流型5则重点考察对于管道中心灵敏度较低区域物体的成像效果。仿真中油、气的相对介电常数分别设定为2.6和1,管内成像区域采用正方形网格剖分,管内有812个像素。基于COMSOL有限元计算软件,获得各流型下仿真的测量电容值,联合MATLAB软件编程实现图像重建算法以进行ECT图像重建。
Landweber算法重建图像时,迭代次数设置为100次;内点法重建图像时,正则化参数α取0.005;GPSR算法重建图像时,拉格朗日因子τ取0.005;OMP算法稀疏度k取30;Landweber算法重建图像时,其重构精度受初始点影响较大,故使用LBP算法重建图像作为其迭代初值。各种算法重建图像如图 1所示。对重建图像进行最优阈值二值化处理后的图像如图 2所示。图 1、图 2各分图从上到下依次为流型1~流型5。
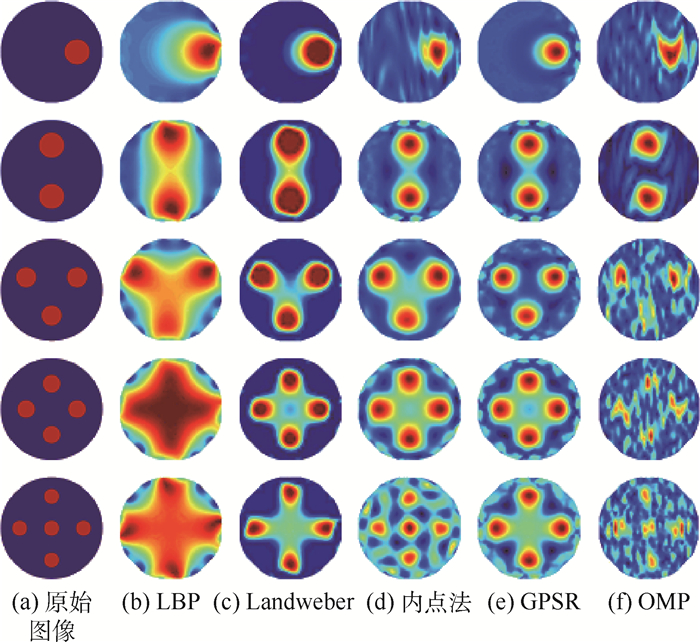 |
| 图 1 初始重建图像 Fig. 1 Initial reconstructed images |
| 图选项 |
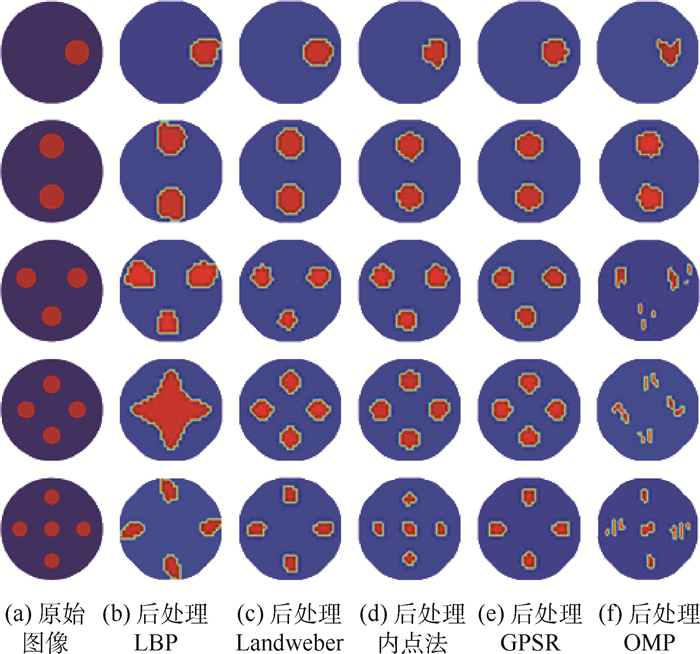 |
| 图 2 基于最优阈值处理的重建图像 Fig. 2 Reconstructed images based on optimal threshold processing |
| 图选项 |
同时,选取重建图像的图像相对误差(Er)及其相关系数(Cc)作为定量评价重建图像质量的指标,其定义为
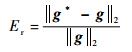 | (14) |
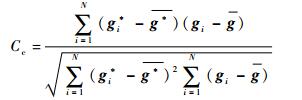 | (15) |
式中:g*为真实分布的归一化值;g及
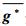
计算得到各算法重建图像的评价指标,如表 1~表 5所示。
表 1 初始重建图像相对误差 Table 1 Relative error of initial reconstructed image
| 流型 | Er | ||||
| LBP | Landweber | 内点法 | GPSR | OMP | |
| 流型1 | 1.405 3 | 0.793 3 | 0.807 8 | 0.590 7 | 0.798 8 |
| 流型2 | 1.238 3 | 0.807 0 | 0.689 1 | 0.675 2 | 0.689 3 |
| 流型3 | 1.570 9 | 0.882 6 | 0.718 9 | 0.774 0 | 0.863 9 |
| 流型4 | 2.002 7 | 1.020 4 | 0.892 5 | 0.883 7 | 0.938 1 |
| 流型5 | 2.052 8 | 1.114 7 | 0.904 1 | 1.091 0 | 0.971 5 |
表选项
表 2 初始重建图像相关系数 Table 2 Correlation coefficient of initial reconstructed image
| 流型 | Cc | ||||
| LBP | Landweber | 内点法 | GPSR | OMP | |
| 流型1 | 0.616 9 | 0.769 6 | 0.813 8 | 0.874 2 | 0.737 5 |
| 流型2 | 0.569 3 | 0.742 3 | 0.843 1 | 0.839 0 | 0.855 8 |
| 流型3 | 0.445 8 | 0.685 0 | 0.730 3 | 0.812 9 | 0.575 2 |
| 流型4 | 0.357 8 | 0.603 0 | 0.662 7 | 0.728 8 | 0.551 6 |
| 流型5 | 0.322 8 | 0.536 6 | 0.675 2 | 0.632 2 | 0.525 6 |
表选项
表 3 后处理重建图像相对误差 Table 3 Relative error of reconstructed image after processing
| 流型 | Er | ||||
| 后处理 LBP | 后处理 Landweber | 后处理内点法 | 后处理 GPSR | 后处理 OMP | |
| 流型1 | 0.854 9 | 0.339 7 | 0.392 2 | 0.277 4 | 0.425 1 |
| 流型2 | 0.784 5 | 0.392 2 | 0.240 2 | 0.219 3 | 0.325 2 |
| 流型3 | 0.872 0 | 0.692 2 | 0.489 5 | 0.102 1 | 0.747 8 |
| 流型4 | 1.258 3 | 0.640 3 | 0.517 4 | 0.408 2 | 0.822 9 |
| 流型5 | 1.030 8 | 0.698 2 | 0.497 6 | 0.559 0 | 0.702 0 |
表选项
表 4 后处理重建图像相关系数 Table 4 Correlation coefficient of reconstructed image after processing
| 流型 | Cc | ||||
| 后处理 LBP | 后处理 Landweber | 后处理内点法 | 后处理 GPSR | 后处理 OMP | |
| 流型1 | 0.630 6 | 0.943 1 | 0.813 8 | 0.958 4 | 0.738 8 |
| 流型2 | 0.696 6 | 0.920 4 | 0.966 6 | 0.972 2 | 0.938 3 |
| 流型3 | 0.681 9 | 0.700 6 | 0.870 6 | 0.994 1 | 0.507 8 |
| 流型4 | 0.552 2 | 0.846 1 | 0.797 4 | 0.915 4 | 0.542 7 |
| 流型5 | 0.500 2 | 0.716 9 | 0.819 3 | 0.799 4 | 0.663 0 |
表选项
表 5 重建图像所用时间 Table 5 Consumed time of image reconstruction
| 流型 | 重建图像所用时间/s | ||||
| LBP | Landweber | 内点法 | GPSR | OMP | |
| 流型1 | 0.013 43 | 4.799 04 | 8.609 49 | 2.779 11 | 0.060 46 |
| 流型2 | 0.014 73 | 4.585 68 | 8.791 92 | 2.623 62 | 0.043 96 |
| 流型3 | 0.011 82 | 5.560 35 | 9.095 21 | 3.539 22 | 0.054 18 |
| 流型4 | 0.013 81 | 5.262 73 | 9.862 51 | 4.610 25 | 0.087 01 |
| 流型5 | 0.015 43 | 5.040 01 | 9.932 23 | 4.735 56 | 0.119 94 |
表选项
分析各种算法重建图像及其评价指标可知,内点法作为目前精度最高的CS理论图像重建算法,对于各种流型均可实现高精度的ECT图像重建,其重建图像质量优于LBP算法和Landweber算法;GPSR算法同样可以实现各种流型的高精度重建,重建图像质量优于LBP算法和Land-weber算法,但由流型5可知,对于管道中心灵敏度较低区域的物体,GPSR算法无法将其重建出来;OMP算法可较高精度地重建简单流型的ECT图像,但对于复杂流型,其成像精度低。
分析各种算法重建图像所用时间可知,内点法重建图像所需迭代次数最多,通过较多的重建时间换取较高精度的重建图像;GPSR算法迭代次数较少,其重建时间少于Landweber算法;OMP算法迭代次数仅取决于稀疏向量稀疏度,重建图像所需时间极短。
故通过定性定量分析各种CS算法重建图像质量及其重建所需时间可知,采用GPSR算法可较高精度的重建多种流型,同时具有较好的实时性;对于简单流型同时重建精度要求较低时,可尝试采用OMP算法进行图像重建,其实时性较高;对于复杂流型同时实时性要求较低时,可采用内点法进行图像重建,管道中心灵敏度较低区域的物体亦可高精确重建出来。
4 结论 1) 基于CS理论建立了ECT系统模型。首先,选择了FFT基进行图像灰度的稀疏化;然后,基于高斯随机方法设计了ECT系统的观测矩阵并计算相应的雅可比矩阵;最后,研究了基于内点法、GPSR算法以及OMP算法的CS重建算法。
2) 进行了相应的仿真实验,结果表明:内点法重建图像精度最高,但耗时也最长;OMP算法速度快,但其重建精度低;而GPSR重建算法重建精度较高,耗时介于内点法与OMP算法之间,因此,需要根据实际应用需求选择对应的图像重建算法。
参考文献
| [1] | 王化祥. 电学层析成像[M].北京: 科学出版社, 2013: 4-20. WANG H X. Electrical tomography[M].Beijing: Science Press, 2013: 4-20.(in Chinese) |
| [2] | 赵玉磊, 郭宝龙, 闫允一. 电容层析成像技术的研究进展与分析[J].仪器仪表学报, 2012, 33(8): 1909–1920. ZHAO Y L, GUO B L, YAN Y Y. Latest development and analysis of electrical capacitance tomography technology[J].Chinese Journal of Scientific Instrument, 2012, 33(8): 1909–1920.(in Chinese) |
| [3] | 郝魁红, 范文茹, 马敏, 等. 平面式电容传感器阵列测量复合材料技术研究[J].传感器与微系统, 2014, 33(2): 35–38. HAO K H, FAN W R, MA M, et al. Research on technology of composite materials measurement by planar capacitance sensor array[J].Transducer and Microsystem Technologies, 2014, 33(2): 35–38.(in Chinese) |
| [4] | 马敏, 周苗苗, 李新建, 等. 基于ECT技术的航空发动机尾气监测系统设计[J].传感器与微系统, 2015, 34(5): 88–91. MA M, ZHOU M M, LI X J, et al. Design of aero-engine off gas monitoring system based on ECT technology[J].Transducer and Microsystem Technologies, 2015, 34(5): 88–91.(in Chinese) |
| [5] | 吴新杰, 黄国兴, 王静文. 粒子滤波算法在ECT图像重建中的应用[J].光学精密工程, 2012, 20(8): 1826–1830. WU X J, HUANG G X, WANG J W. Application of particle filtering algorithm to image reconstruction of ECT[J].Optics and Precision Engineering, 2012, 20(8): 1826–1830.(in Chinese) |
| [6] | DONOHO D L. Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306.DOI:10.1109/TIT.2006.871582 |
| [7] | YU Y, HONG M, LIU F, et al.Compressed sensing MRI using singular value decomposition based sparsity basis[C]//Annual International Conference of the IEEE Engineering in Medicine and Biology Society.Piscataway, NJ:IEEE Press, 2011:5734-5737.http://www.ncbi.nlm.nih.gov/pubmed/21896962 |
| [8] | 吴新杰, 黄国兴, 王静文. 压缩感知在电容层析成像流型辨识中的应用[J].光学精密工程, 2013, 21(4): 1062–1068. WU X J, HUANG G X, WANG J W. Application of compressed sensing to flow pattern identification of ECT[J].Optics and Precision Engineering, 2013, 21(4): 1062–1068.(in Chinese) |
| [9] | 张玲玲, 王化祥, 范文茹, 等. 基于1范数的电阻层析成像图像重建算法[J].天津大学学报, 2011, 44(9): 786–790. ZHANG L L, WANG H X, FAN W R, et al. Image reconstruction algorithm based on 1-norm for electrical resistance tomography[J].Journal of Tianjin University, 2011, 44(9): 786–790.(in Chinese) |
| [10] | 常甜甜, 魏雯婷, 丛伟杰. 电阻抗成像的稀疏重建算法[J].西安邮电学院学报, 2013, 18(2): 92–96. CHANG T T, WEI W T, CONG W J. Electrical impedance tomography based on sparse reconstruction[J].Journal of Xi'an University of Post and Telecom, 2013, 18(2): 92–96.(in Chinese) |
| [11] | 王丕涛, 王化祥, 孙犇渊. 基于l1范数的电容层析成像图像重建算法[J].中国电机工程学报, 2015, 35(18): 4709–4714. WANG P T, WANG H X, SUN B Y. l1-norm-based image reconstruction algorithm for electrical capacitance tomography[J].Proceedings of the CSEE, 2015, 35(18): 4709–4714.(in Chinese) |
| [12] | YE J M, WANG H G, YANG W Q. Image reconstruction for electrical capacitance tomography based on sparse representation[J].IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 89–102.DOI:10.1109/TIM.2014.2329738 |
| [13] | 马坚伟, 徐杰, 鲍跃全, 等. 压缩感知及其应用:从稀疏约束到低秩约束优化[J].信号处理, 2012, 28(5): 609–623. MA J W, XU J, BAO Y Q, et al. Compressive sensing and its application:From sparse to low-rank regularized optimization[J].Signal Processing, 2012, 28(5): 609–623.(in Chinese) |
| [14] | CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory, 2006, 52(2): 489–509.DOI:10.1109/TIT.2005.862083 |
| [15] | BARANIUK R G. Compressive sensing[lecture notes][J].IEEE Trans on Signal Processing Magazine, 2007, 24(4): 118–121.DOI:10.1109/MSP.2007.4286571 |
| [16] | 陈宇, 高宝庆, 张立新, 等. 基于加权奇异值分解截断共轭梯度的电容层析图像重建[J].光学精密工程, 2010, 18(3): 701–707. CHEN Y, GAO B Q, ZHANG L X, et al. Image reconstruction based on weighted SVD truncation conjugate gradient algorithm for electrical capacitance tomography[J].Optics and Precision Engineering, 2010, 18(3): 701–707.(in Chinese) |
| [17] | NATARAJAN B K. Sparse approximate solutions to linear systems[J].SIAM Journal on Computing, 1995, 24(2): 227–234.DOI:10.1137/S0097539792240406 |
| [18] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J].SIAM Review, 2001, 43(1): 129–159.DOI:10.1137/S003614450037906X |
| [19] | SEUNG J K, KOH K, LUSTIG M, et al. An interior-point method for large-scale l1-regularized least squares[J].IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 606–617.DOI:10.1109/JSTSP.2007.910971 |
| [20] | FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction:Application to compressed sensing and other inverse problem[J].IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586–597.DOI:10.1109/JSTSP.2007.910281 |
| [21] | TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666.DOI:10.1109/TIT.2007.909108 |
| [22] | BLUMENSATH T, DAVIES E. Iterative hard thresholding for compressed sensing[J].Applied and Computational Harmonic Analysis, 2009, 27(3): 265–274.DOI:10.1016/j.acha.2009.04.002 |
| [23] | GILBERT A C, INDYK P, IWEN M, et al. Recent developments in the sparse fourier transform:A compressed Fourier transform for big data[J].IEEE Signal Processing Magazine, 2014, 31(5): 91–100.DOI:10.1109/MSP.2014.2329131 |
