备件是对装备进行维修保障的重要物质基础，它的保障程度对于装备的战备完好和任务持续性有直接影响。在传统的备件供应保障模式下，保障组织中的站点有“层级”之分，通常是低层级的站点向高层级的站点申领备件，高层级的站点接收低层级站点发送过来的故障件进行修复，并向低层级的站点供应备件。这种组织结构就是典型的“树状”保障组织结构，它更适用于描述保障站点的“纵向”保障关系；与此并存的还包括横向保障(或者称为横向转运)，即向同级站点而非上级站点申领备件，这种情况的出现往往意味着向相邻站点申请“横向”保障往往要比从上级站点申请“纵向”保障更加经济和高效。对于单纯考虑“纵向”保障的备件库存分析与优化问题，可以参考METRIC系列^[1-3]模型以及其他相关研究^[4-6]。对于库存系统中的横向保障或横向转运，是指同级站点之间的备件流动，根据转运原则、转运时机、转运范围又可以对其进行细分^[7-9]。对于单级别多个站点的库存系统，横向补货策略最早出现在Gross^[10]的文章中，众多的研究表明：当不同站点的缺货成本差别较大时横向保障策略更为有效，且有利于提供整个系统的备件保障效能^[11-14]。
在横向保障模型中，一个中心站点和多个被横向保障的站点组成的系统是较为普遍的研究对象，有很多****对此问题进行了研究。如Lee^[8]针对由一个中心仓库和多个带横向供应时间的地方仓库组成的两级库存系统，在完全共享模式下的3种转运规则进行了研究。Sherbrooke^[15]运用回归分析方法确定两级库存系统的备件延期交货量。Tagaras和Cohen^[16]运用仿真和网格搜索的方法对两级三站点库存系统在4种库存共享策略下的备件成本对比分析。Grahovac和Chakravarty^[17]在Axs?ter^[18]研究的基础上，研究在不同缺货补给时机下的系统备件延期交货量。类似的研究还包括文献[7, 12, 19-20]等。
综上所述，以上问题的主流解决思路是：允许将横向保障的站点看成是一个保障组(即复合站点，内含多个同级站点)，从形式上将其转化成多级库存控制理论研究范畴的问题。而对于横向保障组，已有研究大多假定其中站点属性是完全相同的，即在备件的横向保障策略上不存在任何差别，包括横向保障组内各站点到上级站点的备件周转供应时间、备件需求率、各站点的故障件维修速率等大多均假定相同。此外，绝大多数允许横向保障的库存模型中都忽略横向保障站点间的备件周转供应时间，对于横向转运的方向性也基本没有限制。以上这些做法虽然可以降低数学建模和解析计算的难度，但是这些假设和简化与实际情况并不十分吻合。在现实情况中，由于装备部署、自身状态、使用强度等因素的变化，使得各装备对备件的需求强度往往有所差异；其次，由于不同装备部署站点之间距离相等的情况很少，因而在传统研究中假定各站点的属性基本一致也非常不合理。
针对上述问题，本文针对三站点库存系统提出一种能够综合考虑站点间纵向保障关系和横向保障关系的备件供应保障模型。首先，通过引入站点间备件需求关系的定量描述建立了三站点间的备件供应保障关系，并建立了三站点库存系统的备件延期交货量方程组；其次，运用压缩映射原理判定了方程组解的唯一性，并据此结论给出了方程组的求解算法；最后，通过示例验证了算法的有效性。
1 分析及建模 1.1 问题描述及假设 本文研究三站点间备件供应保障关系如图 1所示。图 1中，实线箭头表示备件的供应方向，虚线箭头表示故障件的流动方向。当站点i产生备件需求时，产生的故障件将分别以概率r_ij(≥0)(i, j=1, 2, 3)，送至站点j进行维修，且1(j=1, 2, 3)。与此同时，对应的站点将以相同的概率向站点i提供备件。在建立备件横向保障模型之前，先给出如下前提假设：① 站点的备件需求服从泊松分布，且相互独立。② 站点的维修资源充足，不存在故障件排队等待维修的情况。③ 故障件不存在修理报废的情况且修复如新。④ 库存系统中故障件及备件的修复时间以及运输时间均相互独立。⑤ 站点库存采用连续盘点的(s, s－1)(s为初始库存量)库存控制策略，即当一个站点向另一个站点申领1个备件时，会将1个故障件送至被申领站点。⑥ 站点间备件完全共享。本文的研究对象主要指装备中的可修件，属于需求率低而单价较高的产品，其经济订货量约等于1，因此采用(s, s－1) 库存控制策略以及上述其他假设是合理的。

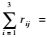
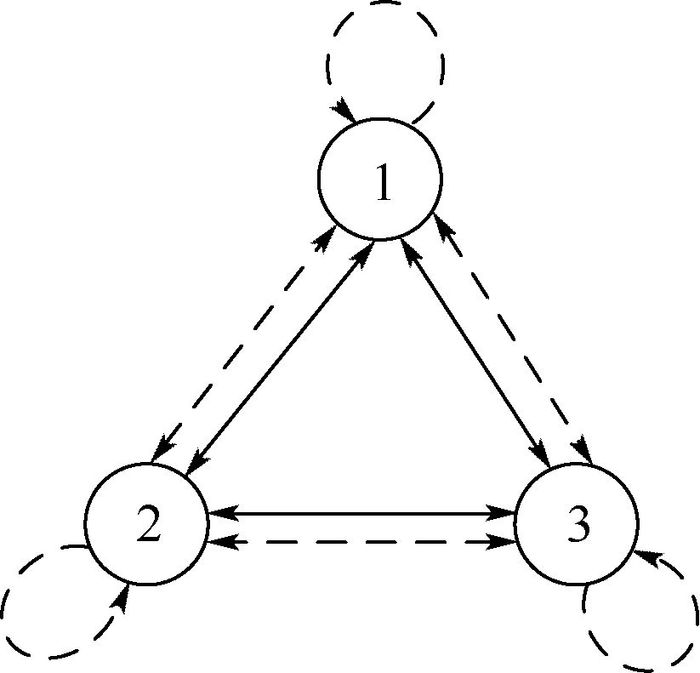图 1 备件和故障件在三站点库存系统中的流动模型 Fig. 1 Transportation model of spares and failure items in inventory systems of three stations

图选项

1.2 模型的建立 显然，在图 1所示备件供应保障系统中，站点i与周边站点的供应保障关系是通过供应保障规则建立起来的，因而站点i的备件延期交货量不但受站点i自身的备件需求率、库存量、故障件的维修周转时间等因素影响，其还受到站点i周边其他站点备件延期交货量(EBO)以及备件补给请求及补给情况等因素的影响。应得备件数量是表征站点备件状态的一个重要变量，它与初始库存量s、可用库存量s_OH和备件短缺数s_BO之间存在一个平衡等式，被称为库存平衡公式。单站点的库存平衡公式为

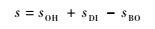(1)

式中:s_DI为应得备件数，它涵盖处于修理、运输环节中的备件数量。
在稳定状态下，可分别列出三站点的库存平衡方程：

(2)

式中:s_i、s_OHⁱ、s_DIⁱ和s_BOⁱ分别为站点i的初始库存量、可用库存量、应得备件数和备件短缺数。
站点i的应得备件数s_DIⁱ包括正在站点i进行维修的故障件、处于运输途中来自站点j(j≠i)的故障件、处于运输途中来自站点j(j≠i)的备件、站点j(j≠i)延迟交付给站点i的备件数量。为了便于表达，定义如下参数。
因为站点j产生备件需求时，站点j将以p_ji的概率向站点i申领备件，与此同时站点j会将等数量的故障件送至站点i进行维修，故

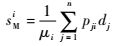(3)

式中：s_Mⁱ为正在站点i进行维修的故障件数；d_i(>0) 为站点i(i=1, 2, 3) 处的备件需求率；μ_i(>0) 为站点i(i=1, 2, 3) 处的故障件修复率；p_ij(i, j=1, 2, 3) 为站点i向站点j申领备件的概率，p_ij≥0，。
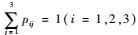
处于运输途中的从站点j运往站点i的故障件数量，与站点j的备件需求率和两站点间的转运时间有关，故

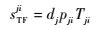(4)

式中：s_TF^ji为处于运输途中的从站点j运往站点i的故障件数量；T_ij(i, j=1, 2, 3) 为站点i向站点j运送备件或故障件的时间，T_ij>0。
处于运输途中的从站点j运往站点i的备件数量，它与站点i的备件需求率和两站点间的转运时间有关，故

(5)

式中：s_TP^ji为处于运输途中的从站点j运往站点i的备件数量。
站点j延迟交付给站点i的备件数量，它与站点j所有延迟交付的备件中站点i所占比例相关(且为正比)，故

(6)

式中：s_BO^j为站点j的备件短缺数，它的期望值为EBO_j；s_BO^ji为站点j延迟交付给站点i的备件数量。
由此可以得到通用的备件横向保障模型：

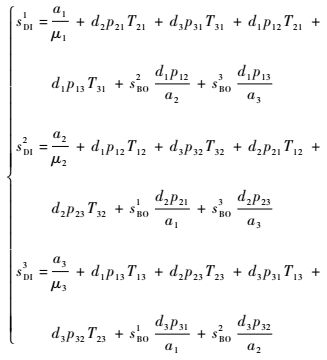(7)

式中:a₁=d₁p₁₁+d₂p₂₁+d₃p₃₁; a₂=d₁p₁₂+d₂p₂₂+d₃p₃₂; a₃=d₁p₁₃+d₂p₂₃+d₃p₃₃。延期交货量和应得备件数量的关系为

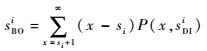(8)

式中：s_BOⁱ为站点i的备件短缺数，它的期望值为EBO_i；P为概率。因而0＜s_BO≤s_DI。令s_BO¹=α₁s_DI¹(0＜α₁≤1)，s_BO²=α₂s_DI²(0＜α₂≤1)，s_BO³=α₃s_DI³(0＜α₃≤1)，则式(7) 最终可以写成

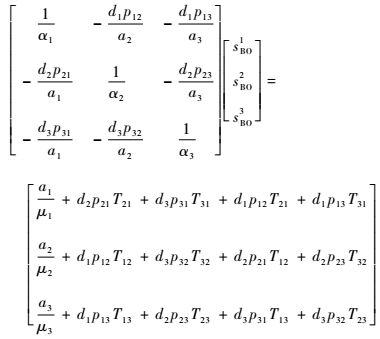(9)

2 模型解唯一性判定 令，则由a₁、a₂、a₃的定义可知：，。
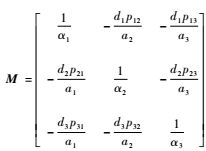
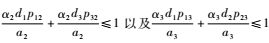
令。
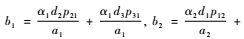
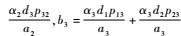
情况1? b₁＜1且b₂＜1且b₃＜1，此时矩阵M为主对角占优矩阵，因此M可逆。
情况2? 1－b₁>0, 1－b₂=0, 1－b₃=0, 则。如果，则|M|=0，M不可逆。但是此时必须有α₂=1、α₃=1、p₁₂=p₂₂=0及p₁₃=p₃₃=0，进而可以推出p₁₁=1。此时方程组不相容，无解。因此情况2不可能出现。同理可证1－b₁=0、1－b₂>0、1－b₃=0的情况和1－b₁=0、1－b₂=0、1－b₃>0的情况也不可能出现。
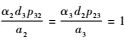
情况3? 1－b₁>0，1－b₂>0，1－b₃=0，则，由题设知|M|表达式中各项均大于等于0，又因为，所以|M|≠0，因此情况3中矩阵M可逆。同理，在1－b₁>0、1－b₂=0、1－b₃>0的情况和1－b₁=0、1－b₂>0、1－b₃>0的情况中，矩阵M可逆。
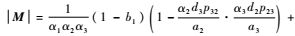
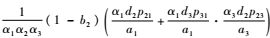
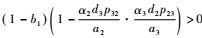
情况4? 1－b₁=0且1－b₂=0且1－b₃=0，则由式(9) 可知

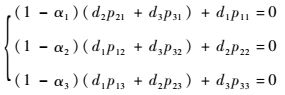(10)

因为d_i>0，0≤1－α_i＜1，所以式(10) 成立时必须有

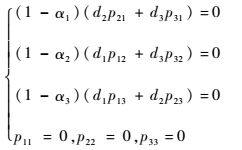(11)

对于式(11)，如果p₁₁=0，p₂₂=0，p₃₃=0且α₁=1，α₂=1，α₃=1，那么式(9) 方程不相容，因而无解；如果p₁₁=0，p₂₂=0，p₃₃=0且d₂p₂₁+d₃p₃₁=0，d₁p₁₂+d₃p₃₂=0，d₁p₁₃+d₂p₂₃=0，那么同样存在不相容的情况。
综上所述，矩阵M始终可逆，因而对于给定的输入方程始终有唯一解。
3 模型的求解与算例分析 3.1 模型的求解 将式(9) 写成如下形式：

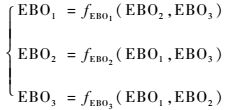(12)

式中：EBO为备件延期交货量的期望值。由第2节分析可知式(9) 有唯一解，这也意味着式(9) 所列方程确定的映射关系为压缩映射，因而可以运用迭代算法求出模型的解：通过设定初值(EBO₁, EBO₂)，利用公式(EBO₁^(k), EBO₂^(k))=f(EBO₁^(k－1), EBO₂^(k－1))建立的迭代关系，依据以及，通过反复迭代计算得到系统最终的逼近解(EBO₁^*, EBO₂^*)。此外，在迭代计算过程中，可以选定相邻两次迭代目标函数差值与给定差值容限ε的大小关系作为终止迭代运算的判据。得到算法迭代步骤如图 2所示。

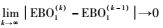
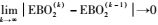
图 2 系统延期交货量迭代方法计算流程 Fig. 2 Calculation process of EBO with iteration method

图选项

3.2 算例分析 假定站点1、2、3处的备件需求率分别为：d₁=0.12，d₂=0.23，d₃=0.41；站点1向自身及其他站点产生备件需求的概率分别为：p₁₁=0.72，p₁₂=0.21，p₁₃=0.07，站点2向自身及其他站点产生备件需求的概率分别为：p₂₁=0.12，p₂₂=0.76，p₂₃=0.12，站点3向自身及其他站点产生备件需求的概率分别为：p₃₁=0.18，p₃₂=0.22，p₃₃=0.6；故障件在站点1、2、3的维修周转速率分别为：μ₁=0.12，μ₂=0.23，μ₃=0.41；从站点1到站点2和站点3的运输时间分别为：T₁₂=78，T₁₃=93，从站点2到站点1和站点3的运输时间分别为：T₂₁=113，T₂₃=156，从站点3到站点1和站点2的运输时间分别为：T₃₁=97，T₃₂=105；站点1、站点2和站点3的初始库存量分别为：s₁=7，s₂=9，s₃=7。依据此输入可以计算得到：EBO₁=10.46，EBO₂=12.91，EBO₃=27.85。如果变动各个站点处的备件需求概率，可以得到3个站点总的EBO随备件需求概率的变化曲线。例如，可以通过变动p₁₁得到EBO总和与p₁₁之间的变化曲线，见图 3。

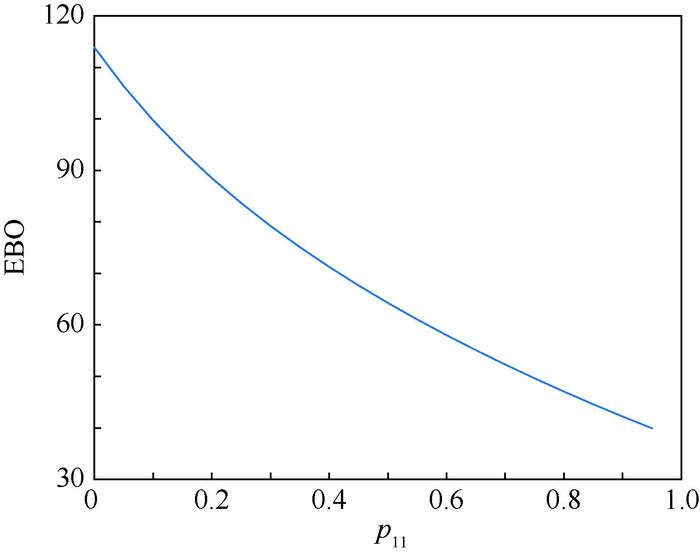图 3 三站点总的EBO随p11变化曲线 Fig. 3 Curve of total EBO within three stations versus p11

图选项

通过分析可以得知：在上述输入下，如果增加站点1处故障件在本地维修的概率，那么将有助于降低系统总的EBO，因而当p₁₁=1时系统总的EBO将达到最小值。很明显，针对不同输入将得到不同的结论。当然，还可以针对其他参数进行敏感性分析以及比较分析，但这不是本文的研究重点，因而不在此赘述。
4 结论 1) 本文虽然通过弱化保障组织内站点间的层级关系建立了较为通用的备件供应保障关系模型，但是文中结论也是在众多的假设和限定的基础上得来的，因而所得模型也会与实际情况存在一定的出入。
2) 在很多考虑横向保障或横向转运的相关研究中，横向保障往往是在备件缺货时才被考虑。这也就意味着站点的备件需求概率与站点的备件满足率相关，而本文中模型并未考虑这种情况。作者认为，针对这种较为复杂的情况，只要在本文所给模型的基础上，另构造一个备件需求概率或备件满足率的柯西数列，基于本文给出的计算流程建立一个两层迭代算法即可。
3) 尽管本文提出的模型存在一定的应用局限性(在现实中备件供应保障站点的数目往往会远大于3个)，但是文中的研究方法具有很好的扩展性，可以为后续复杂对象的研究提供一定的理论参考。
致谢    
感谢北京航空航天大学可靠性与系统工程学院马麟、王乃超两位老师的宝贵意见。
参考文献

[1]	SHERBROOKE C C. METRIC:A multi-echelon technique for recoverable item control[J].Operations Research, 1968, 16(1): 122–141.DOI:10.1287/opre.16.1.122
[2]	MUCKSTADT J A. A model for a multi-item, multi-echelon, multi-indenture inventory system[J].Management Science, 1973, 20(4): 472–481.
[3]	SHERBROOKE C C. VARI-METRIC:Improved approximations for multi-indenture, multi-echelon availability models[J].Operations Research, 1986, 34(8): 311–319.
[4]	王乃超, 康锐. 基于备件保障概率的多级库存优化模型[J].航空学报, 2009, 30(6): 1043–1047. WANG N C, KANG R. Optimization of multi-echelon repairable item inventory systems with fill rate as objective[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1043–1047.(in Chinese)
[5]	刘任洋, 李庆民, 李华. 基于横向转运策略的可修件三级库存优化模型[J].航空学报, 2014, 35(12): 3341–3349. LIU R Y, LI Q M, LI H. Optimal model of three-echelon inventory for repairable spare parts with lateral transshipments strategy[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3341–3349.(in Chinese)
[6]	阮曼智, 彭英武, 李庆民, 等. 基于体系保障度的装备备件三级库存方案优化[J].系统工程理论与实践, 2012, 32(7): 1623–1630. RUAN M Z, PENG Y W, LI Q M, et al. Optimization of three-echelon inventory project for equipment spare parts based on system support degree[J].Systems Engineering-Theory & Practice, 2012, 32(7): 1623–1630.DOI:10.12011/1000-6788(2012)7-1623(in Chinese)
[7]	LEE Y H, JUNG J W, JEON Y S. An effective lateral transshipment policy to improve service level in the supply chain[J].International Journal of Production Economics, 2007, 106(1): 115–126.DOI:10.1016/j.ijpe.2006.05.007
[8]	LEE H L. A multi-echelon inventory model for repairable items with emergency lateral transshipments[J].Management Science, 1987, 33(10): 1302–1316.DOI:10.1287/mnsc.33.10.1302
[9]	TAGARAS G. Pooling in multi-location periodic inventory distribution systems[J].Omega, 1999, 27(1): 39–59.DOI:10.1016/S0305-0483(98)00030-9
[10]	GROSS D. Centralized inventory control in multi-location supply systems[M].Stanford: Stanford University Press, 1963: 47-84.
[11]	KUKREJA A, SCHMIDT C P, MILLER D M. Stocking decisions for low-usage items in a multi-location inventory system[J].Management Science, 2001, 47(10): 1371–1383.DOI:10.1287/mnsc.47.10.1371.10263
[12]	AXS?TER S. Evaluation of unidirectional lateral transshipments and substitutions in inventory systems[J].European Journal of Operational Research, 2003, 149(2): 438–447.DOI:10.1016/S0377-2217(02)00447-2
[13]	KUKREJA A, SCHMIDT C P. A model for lumpy demand parts in a multi-location inventory system with transshipments[J].Computers & Operations Research, 2005, 32(8): 2059–2075.
[14]	WONG H, VAN H G J, CATTRYSSE D, et al. Multi-item spare parts systems with lateral transshipments and waiting time constraints[J].European Journal of Operational Research, 2006, 171(3): 1071–1093.DOI:10.1016/j.ejor.2005.01.018
[15]	SHERBROOKE C C. Multi-echelon inventory systems with lateral supply[J].Naval Research Logistics, 1992, 39: 29–40.DOI:10.1002/(ISSN)1520-6750
[16]	TAGARAS G, COHEN M A. Pooling in two-location inventory systems with non-negligible replenishment lead-times[J].Management Science, 1992, 38(8): 1067–1083.DOI:10.1287/mnsc.38.8.1067
[17]	GRAHOVAC J, CHAKRAVARTY A. Sharing and lateral transshipment of inventory in a supply chain with expensive low demand items[J].Management Science, 2001, 47(4): 579–594.DOI:10.1287/mnsc.47.4.579.9826
[18]	AXS?TER S. Modeling emergency lateral transshipments in inventory systems[J].Management Science, 1990, 36(11): 1329–1338.DOI:10.1287/mnsc.36.11.1329
[19]	TAGARAS G, VLACHOS D. Effectiveness of stock transshipment under various demand distributions and no negligence transshipment times[J].Production and Operational Management, 2002, 11(2): 183–198.
[20]	OLSSON F. An inventory model with unidirectional lateral transshipments[J].European Journal of Operational Research, 2010, 200(3): 725–732.DOI:10.1016/j.ejor.2009.01.024