航空、航天、汽车等工业中的复杂充液成形管件的成形通常包括管坯的制备、弯曲、预成形、充液成形,端面切割等工序。管材弯曲过程中,管材弯曲内侧通常受压增厚,弯曲外侧则受拉而减薄。而在充液成形过程中,由于侧推力的作用和管材贴模顺序的不可控导致变形过程更无规律所循。在管材贴模之前对管材的应力分析通常不考虑厚向应力,认为管材处于平面应力状态,而当管材贴模后管材的厚向应力等于内压力,由于内压力、侧推力和摩擦力等的综合作用,使管材的变形行为更为复杂。相比板材的成形过程,复杂的变形历史和变形路径使管材的成形性能与失效分析更为困难。
金属板料成形中通常采用成形极限图(Forming Limit Diagram, FLD)来评估材料的成形性能。FLD是由Keeler、Backofen[3]和Goodwin[4]在实验的基础上提出的,并确立了完整的实验方法。之后,随着管材充液成形技术的广泛应用,很多****便开展了管材成形极限的研究。Muammer和Taylan[5]结合塑性理论、薄膜理论和薄-厚壁管理论提出了管材胀形过程中的塑性屈曲、起皱和破裂预测的理论模型,并通过实验对模型进行了验证。Kim等[6]认为管材充液成形过程中的破裂不同于屈曲和起皱,它是一种不可复原的失效形式,并基于塑性失稳理论和韧性断裂理论提出了一种预测破裂的模型,并用试验进行了验证。Hwang[7]和Chen[8]等利用管材胀形实验获得了完整的FLD,通过理论计算和数值模拟保证了实验过程的线性加载。理论研究方面Swift和Hill首先结合分散性失稳理论和集中性失稳理论得到了完整的成形极限图,但是由于连续性假设,材料在双拉状态下无法预测成形极限,因而适于范围局限。而基于沟槽的M-K理论更为被****广泛认可并得到修正和发展。郎利辉等[9]在研究铝合金的成形极限考虑了厚向应力的作用对M-K模型进行了修正。崔晓磊等[10]建立了以厚向应力为第3轴的三维成形极限。杨希英等[11]将韧性断裂准则嵌入到M-K模型进行修正。
但是对于管材的充液成形往往需要多道次成形,其加载路径呈现出明显的非线性。理论和实验表明用应变表示的FLD的形状是与加载路径相关的[12-13]。Stoughton[14]提出一种基于应力的成形极限图(SFLD), 并且证明应力成形极限图是路径无关的。因此SFLD吸引了众多****的广泛关注。Yoshida和Kuwabara[15]利用两步线性应力加载的管材胀形试验获得了SFLD,并且发现SFLD不是完全路径无关的,并且受到给定路径的硬化行为的影响。当加载较大的预应变或者应变路径的突变都会导致SFLD的路径相关。由于变形过程中的应力变化很难检测,因此SFLD并未得到广泛的应用。
随着航空航天和汽车工业的轻量化发展趋势,弯曲异性截面充液成形管件的需求日益广泛。因此研究弯管胀形过程的变形行为和失效方式对充液成形的工艺设计具有重要意义。当管材经过弯曲变形后,由于几何形状的变化导致管材胀形过程中的应力分布及变形方式也会相应地发生变化。同时管材的弯曲也会使其材料产生不同程度的硬化,从而影响其胀形过程的失效形式。
1 管材弯胀理论模型 1.1 内压作用下环壳的应力应变表达 为了便于分析,将管材的弯曲段等效成薄壁圆环的一部分如图 1所示。假设圆环的材料是连续的、一致的和各向同性的。根据薄膜理论可得
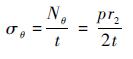 | (1) |
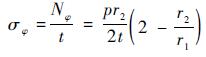 | (2) |
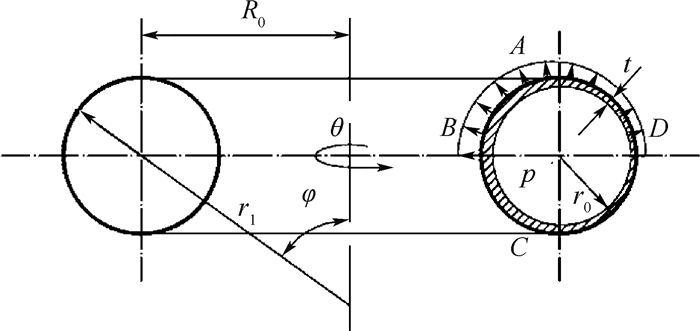 |
| A、B、C、D——管材截面在水平和竖直方向上的顶点。 图 1 环壳胀形理论模型 Fig. 1 Theoretical model of an internally pressurized torus |
| 图选项 |
式中:σθ和σφ分别为管材的轴向应力和环向应力;Nθ和Nφ分别为管材所受的轴向力和环向力;p为内压力;t为环壳的厚度;r0、r1和r2分别为截面圆半径、壳体经线上任一点的曲率半径、经线上任一点垂直于经线的平面与中面相割形成的曲线在这一点的曲率半径,对于环壳有
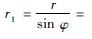
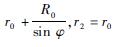
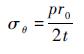 | (3) |
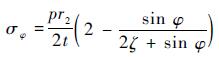 | (4) |
式中:ζ=R0/(2r0)为相对弯曲半径。忽略环壳胀形过程中的厚向应力,认为环壳在胀形过程中处于平面应力状态,则等效应力可表达为
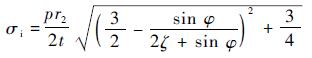 | (5) |
根据增量理论可得
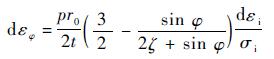 | (6) |
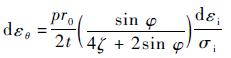 | (7) |
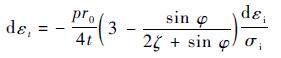 | (8) |
式中:εφ、εθ、εt和εi分别为环向应变、轴向应变、厚向应变和等效应变。
1.2 内压作用下环壳的应力应变的变化规律 由式(3) 可知,在给定规格的环壳和内压力的情况下,轴向应力是与环向角度φ无关的函数,环向应力则是轴向应力的函数,因此定义应力比k=σφ/σθ,应力比k的变化也能够反应环向应力的变化规律,kout、kin和ktop分别为管材弯曲外侧、中性面及内侧的应力比。
图 2中可以看出,在内压力p的作用下管材弯曲内侧的环向应力最大,中性面上其次,弯曲外侧最小。相对弯曲半径对中性面的应力大小没有影响。弯曲外侧,环向应力随着相对弯曲半径的增加而增加,但是增加幅度平缓,数值上的变化量小于0.5σθ;而对于弯曲内侧,环向应力随着相对弯曲半径的增加呈减小趋势,尤其当ζ < 2.5时,相对弯曲半径越小环向应力增加越急剧,当ζ > 2.5时弯曲内侧环向应力变化趋于平坦。
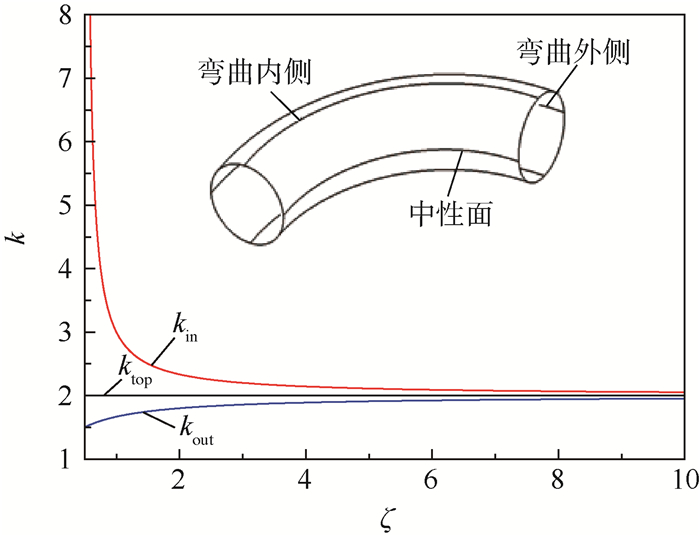 |
| 图 2 参数k随相对弯曲半径的变化规律 Fig. 2 Parameter k's variation pattern with relative bending radius |
| 图选项 |
图 3中可以看出对于弯曲外侧相对弯曲半径对应力比的影响较小(kmax-kmin < 0.5,kmax和kmin分别为k的最大值和最小值),并且呈递减分布。而对于弯曲内侧(-90°~0°),相对弯曲半径越小弯曲内侧的应力比越大,且在最内侧达到极值点。当ζ > 1.25变化趋于平缓。可以看出相对弯曲半径对弯曲内侧应力分布的影响更为严重。
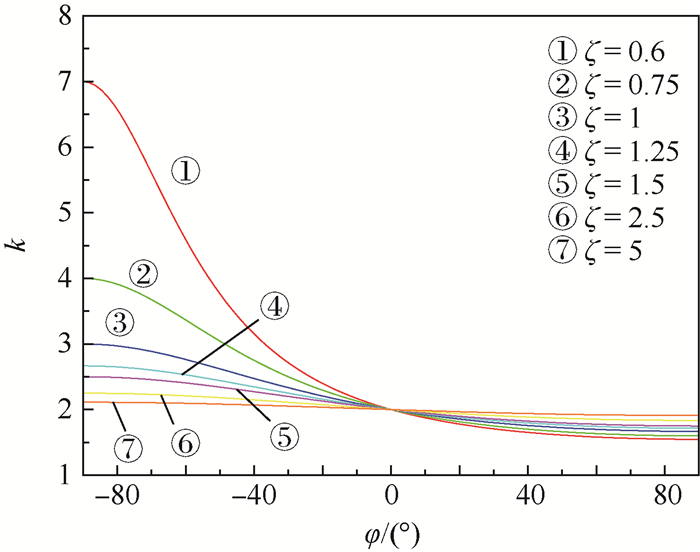 |
| 图 3 参数k沿截面圆环向的变化规律 Fig. 3 Parameter k's variation pattern in circumferential direction |
| 图选项 |
对于环壳必有关系式ζ > 0.5成立,图 4中可以看出在胀形过程中环壳在截面圆环向是拉长的变形,在弯曲内侧的伸长量达到最大;厚向是缩短的变形,即全局减薄,而在弯曲内侧的减薄量最大;圆环的轴向在弯曲内侧是缩短的变形而弯曲外侧是伸长的变形。同时也可以看出相对弯曲半径越小,则胀形过程中弯曲内侧的变形越大,而弯曲外侧的变形量越小。从而也表明相对弯曲半径对弯曲内侧的应变分布影响较大,而弯曲外侧的变形对相对弯曲半径的变化不敏感。
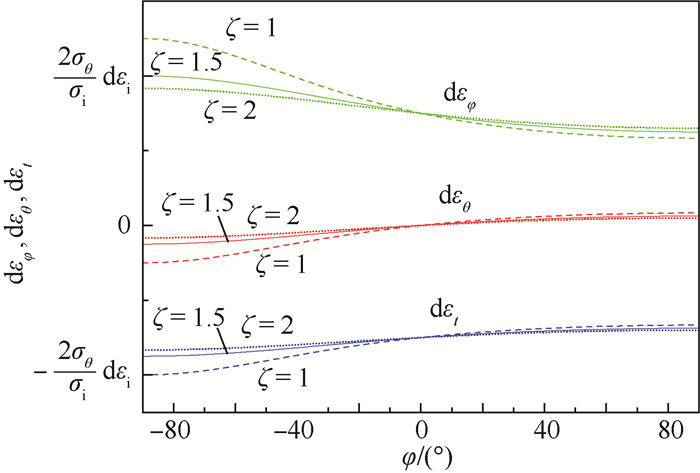 |
| 图 4 应变增量沿截面圆环向的变化规律 Fig. 4 Strain increment variation pattern in circumferential direction |
| 图选项 |
2 理论模型的有限元分析验证 为了验证上述理论模型的适用性,分别对理想等壁厚的圆环和两端直段约束的弯管进行自由胀形过程的有限元分析。由于薄膜理论是基于小挠度假设的基础上得出的,对于金属大的塑性变形是否适用尚不明确,因此本次研究把胀形过程中弹性变形和塑性变形典型阶段的应力分布分别讨论。
应力分布的理论与有限元分析模型对比,如图 5所示。环壳和弯管在胀形过程环向应力的有限元分析和理论结果较为吻合,尤其在弹性变形阶段,其应力沿剖面圆的环向从弯曲内侧到弯曲外侧依次减小。在塑性变形阶段,环向应力分布的趋势与理论模型相同,但数值上有偏差,弯曲内侧的理论值偏大而弯曲外侧的理论值偏小,但其最大偏差都不超过15%。而轴向应力与理论值的结果偏差较大,除了环壳弹性变形阶段。一方面是由于薄膜理论的小挠度基本假设对大变形的塑性阶段适用性较差,另一方面在弯管的自由胀形初期,由于内压力较小弯管两端的直段有模具之间的摩擦力较小,管材没有完全处于平衡状态,导致弯管弹性变形阶段的偏差较大。尽管如此,等效应力分布的模拟结果与理论结果的一致性较好。因此理论解析的结果能够较好地表征弯管在自由胀形状态下的内力分布情况。变形各阶段有限元分析具体的应力分布结果如图 6所示。
 |
| 图 5 应力分布的理论分析与有限元结果对比 Fig. 5 Comparison of stress distribution between theoretical analysis and FE results |
| 图选项 |
 |
| 图 6 环壳与弯管自由胀形状态下的应力分布 Fig. 6 Stress distribution of torus and bent tube in free-expansion state |
| 图选项 |
3 考虑弯曲影响的管材自由胀形失效分析 3.1 管材弯曲过程的变形特点 在典型的充液成形低碳钢管材零件中,其塑性5%~15%消耗在管材制备过程中,20%~30%消耗在管材弯曲过程中,5%~15%消耗在充液成形过程中[16]。可以看出,管材弯曲过程变形消耗的管材的塑性最多,因此研究管材弯曲过程的变形特点是十分必要的。管材弯曲的方法包括:压弯、滚弯、推弯、绕弯等,其中绕弯是这些弯曲工艺中最简单、高效、高精度的成形方法。
典型的弯曲模具结构,如图 7所示。在管件绕弯过程中,夹模夹紧力是弯曲的主动力,同时还起到增大管件的周向压应力、提高材料塑性的作用,但由于施力位置远离形变区域,故对成形质量影响有限;压模压力既可看作是夹紧力的被动力,对抗管件的回弹力防止其翘曲,又可看作是主动力,使管件紧贴模具,限制材料流动的空间,其作用机理与夹紧力类似;弯曲模和防皱模支撑力是被动力,其大小由相应的模具主动力和管件回弹力决定,主要作用是与其他模具一起将管件限制在狭小空间内,防止其起皱;助推力是辅助力,以静摩擦力的形式由压力模施加到管件外侧,通过形成与管件外侧内力矩方向相反的力矩来减小其所受拉应力,在限制壁厚减薄、伸长、回弹等方面有一定作用。
 |
| 图 7 典型的弯曲模具结构 Fig. 7 Typical bending mold structure |
| 图选项 |
在绕弯的过程中由于摩擦力的作用而使得管材沿轴向全局伸长。管材壁厚的变化只是第3向主应变,无法体现板料的全局变形,材料的全局变形通常用等效应变表示。典型位置的全局变形如图 8所示。对于弯曲外侧,弯曲中间截面等效应变值达到最大。而由于管材与弯曲模之间的摩擦力作用,使得管材弯曲内侧和中性层的主应变的压缩变形聚集在弯曲的后半程,从而使其等效应变沿θ方向呈现依次减小的趋势。此外,从图 8(a)中也可以看出左侧(θ=0°~45°)的变形量要大于右侧(θ=45°~90°)。即弯曲过程后半阶段的变形整体上要大于前半阶段的变形。
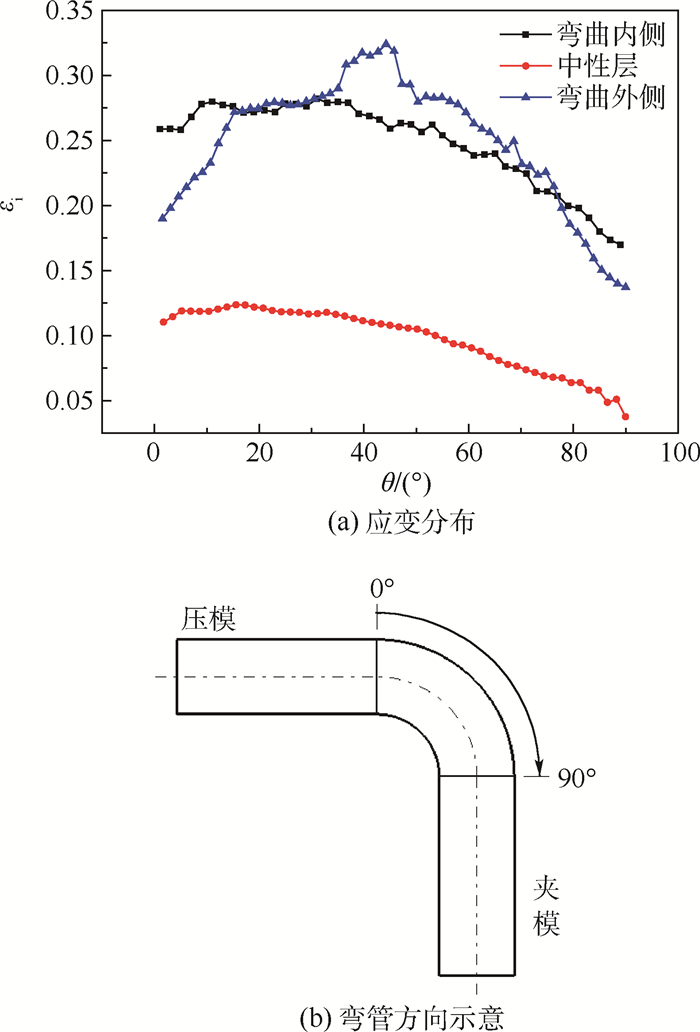 |
| 图 8 典型位置沿轴向等效应变分布规律 Fig. 8 Equivalent strain distribution rule in axial direction at typical location |
| 图选项 |
3.2 弯曲管材胀形过程失效形式分析 假设管材弯曲过程按照幂函数规律硬化
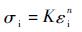 | (9) |
式中:K为应变硬化系数;n为应变硬化指数。
从图 8和式(9) 中也可以看出, 在管材弯曲过程的前半阶段(靠近夹模处的弯曲段)的硬化程度要小于管材弯曲的后半阶段(靠近压模的弯曲段)。当弯曲后的管材加载内压力后,靠近夹模处的弯曲段强度较低, 首先发生屈服,因此此段材料也容易最先发生破裂。在沿截面圆的方向上,如图 9所示, 在弯曲段的中性层上所需的胀形压力最小,且发生的塑性变形量最大。同时结合式(5) 也可以看出, 弯曲内所需的胀形压力小于弯曲内侧,但两侧的变形量基本相似。综上所述, 弯管胀形过程的破裂位置分布于位于管材的边缘靠近夹模的中性层处。
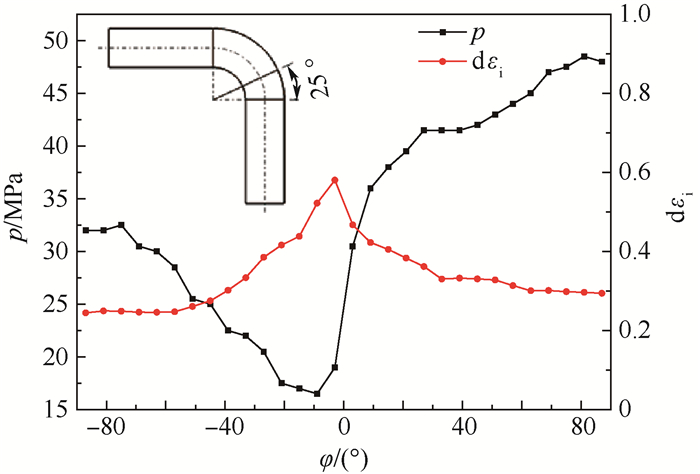 |
| 图 9 管材弯胀过程中所需内压力及各截面应变增量分布 Fig. 9 Internal pressure needed during tube bending and expansion process and strain increment distribution at cross-sections of a bent tube |
| 图选项 |
尽管成形极限图对于多道次成形和非线性加载路径的成形过程的判断存在较大误差,但是成形极限图的操作简单, 易于判断, 在实际的板料成形工程中仍然得到广泛的应用。从FLD中可以直观地看出,当成形过程的应变路径与纵轴重合,即材料的变形处于平面应变状态时,板料的成形性能最差。变形路径的倾斜度越大,则成形性能越好。管材弯曲胀形的有限元分析如图 10所示,分别选取弯曲边缘破裂危险段中弯曲内侧,弯曲中性层和弯曲外侧的单元观察其应变路径,可以看出弯曲中性层处的应变路径趋近FLD中的纵轴即平面应变状态。因此也从另一方面说明中性层最先容易发生开裂。通过对相对弯曲半径为2.5,弯曲角度为60°的低碳钢进行胀形实验(如图 11所示),其结果与数值模拟吻合。
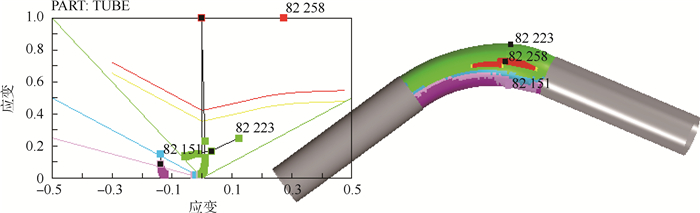 |
| 图 10 弯管胀形典型单元的应变路径 Fig. 10 Strain paths at different typical points of a pressurized bent tube |
| 图选项 |
 |
| 图 11 弯管的自由胀形实验 Fig. 11 Free-expansion experiment of bent tubes |
| 图选项 |
如果管材过度弯曲使得弯曲外侧受拉消耗了过多的塑性,则结果会与上述的讨论结果有所不同。过度弯曲的管材弯曲外侧的塑性变形最为严重,接近破裂极限(如图 12所示),胀形后一旦发生塑性变形就可能发生破裂(如图 13所示)。胀形过程中典型截面上应力和应变增量分布如图 13所示,弯曲外侧由于过度减薄使其自由胀形过程中等效应力最大,使管材早于其他区域发生塑性变形,因此其胀形期间的变形量也最大。此情况的胀形实验样件如图 14所示。
 |
| 图 12 过度弯曲的管材自由胀形过程中的应变路径 Fig. 12 Strain paths of a bent tube losing most of formability during free expansion process |
| 图选项 |
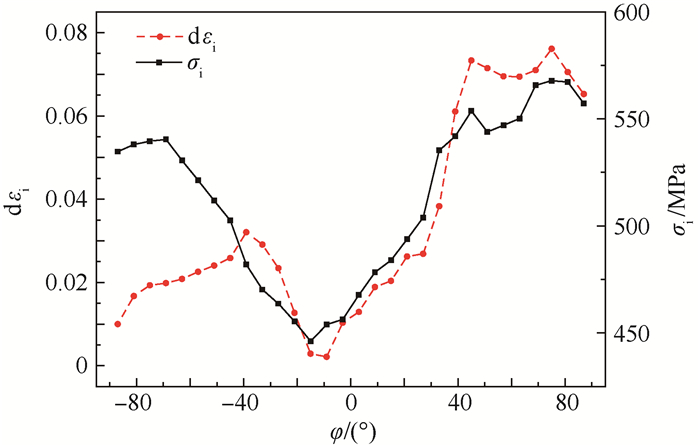 |
| 图 13 过度弯曲的管材自由胀形过程典型截面上的等效应力和应变增量分布 Fig. 13 Equivalent stress and strain increment distribution of a bent tube losing most of formability at typical cross-section during free expansion process |
| 图选项 |
 |
| 图 14 过度弯曲的管材自由胀形过程实验样件 Fig. 14 Experimental sample of a bent tube losing most of formability during free expansion process |
| 图选项 |
4 结论 1) 对于等壁厚理想的弯管在自由胀形过程中,其环向应力沿截面圆从弯曲最内侧至弯曲最外侧呈递减分布,且弯曲内侧的变化率大于弯曲外侧。而轴向应力则在截面圆上的分布一致。
2) 理想等壁厚弯管自由胀形过程中弯曲内侧的环向应力分布随着弯曲半径的增大而减小,而弯曲外侧随着相对弯曲半径的增加而增加。当ζ < 2.5时弯曲内侧的应力分布对相对弯曲半径的敏感程度比弯曲外侧高。
3) 理想等壁厚弯管的自由胀形过程中,弯曲外侧是环向和轴向双向受拉减薄的变形。而弯曲内侧则是环向受拉轴向受压壁厚减薄的变形。
4) 在管材绕弯工艺过程中,弯曲外侧的最大变形区域位于弯曲的中间段,而对于弯曲内侧和中性层上最大变形则发生在弯曲端部靠近压模处。
5) 考虑弯曲影响的管材自由胀形的破裂位置通常位于弯曲的端部靠近夹模的中性层处,而过度弯曲时管材胀形的破裂位置则位于弯曲的外侧。
参考文献
| [1] | ZENG Y S, LI Z Q. Experimental research on the tube push-bending process[J].Journal of Material Processing Technology, 2002, 122(2-3): 237–240.DOI:10.1016/S0924-0136(02)00027-4 |
| [2] | 苑世剑. 现代液压成形技术[M].北京: 国防工业出版社, 2009: 8-9. YUAN S J. Modern hydroforming technology[M].Beijing: National Defence Industry Press, 2009: 8-9.(in Chinese) |
| [3] | KEELER S P, BACKOFEN W A. Plastic instability and fracture in sheets stretched over rigid punches[J].ASM Transactions Quarterly, 1963, 56: 25–48. |
| [4] | GOODWIN G M.Application of strain analysis to sheet metal forming in the press shop:680093[R]. Warrendale, PA:SAE, 1968. |
| [5] | MUAMMER K, TAYLAN A. Prediction of forming limits and parameters in the tube hydroforming process[J].International Journal of Machine Tools & Manufacture, 2002, 42(1): 123–138. |
| [6] | KIM S W, SONG W J, KANG B S, et al. Analytical and number approach to prediction of forming limit in tube hydroforming[J].International Journal of Mechanical Sciences, 2005, 47(7): 1023–1037.DOI:10.1016/j.ijmecsci.2005.02.011 |
| [7] | HWANG Y M, LIN Y K, CHUANG H C. Forming limit diagrams of tubular materials by bulge test[J].Journal of Material Processing Technology, 2009, 209(11): 5024–5034.DOI:10.1016/j.jmatprotec.2009.01.026 |
| [8] | CHEN X F, LI S H, YU Z Q, et al. Study on experimental approaches of forming limit curve for tube hydroforming[J].International Journal of Advanced Manufacturing Technology, 2012, 61(1): 87–100. |
| [9] | LANG L H, CAI G S, LIU K N, et al. Investigation on the effect of through thickness normal stress on forming limit at elevated temperature by using modified M-K model[J].International Journal of Material Forming, 2015, 8(2): 211–228.DOI:10.1007/s12289-014-1161-3 |
| [10] | 崔晓磊, 王小松, 林艳丽, 等. 管材流体压力成形三维成形极限图[J].塑性工程学报, 2014, 21(5): 1–5. CUI X L, WANG X S, LIN Y L, et al. Three-dimension forming limit diagram for fluid pressure forming of tubes[J].Journal of Plasticity Engineering, 2014, 21(5): 1–5.(in Chinese) |
| [11] | 杨希英, 郎利辉, 刘康宁, 等. 基于修正M-K模型的铝合金板材成形极限图预测[J].北京航空航天大学学报, 2015, 41(4): 675–679. YANG X Y, LANG L H, LIU K N, et al. Prediction of forming limit diagram of AA7075-O aluminum alloy sheet based on modified M-K model[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 675–679.(in Chinese) |
| [12] | GRAF A, HOSFORD W. Calculations of forming limit diagrams for changing strain paths[J].Metallurgical Transactions A, 1993, 24: 2503–2512.DOI:10.1007/BF02646529 |
| [13] | KLEEMOLA H J, PELKKIKANGAS M T. Effect of predeformation and strain path on the forming limits of steel copper and brass[J].Sheet Metal Industries, 1977, 63: 591–599. |
| [14] | STOUGHTON T B. A general forming limit criterion for sheet metal forming[J].International Journal of Mechanical Sciences, 1999, 42(1): 1–27. |
| [15] | YOSHIDA K, KUWABARA T. Effect of strain hardening behavior on forming limit stresses of steel tube subjected to nonproportional loading paths[J].International Journal of Plasticity, 2007, 23(7): 1260–1284.DOI:10.1016/j.ijplas.2006.11.008 |
| [16] | SINGH H. Computer simulation of tubular hydroforming[J].Tube & Pipe Journal, 2000, 11: 8–13. |
