最近几十年,世界各国****提出了许多全色锐化方法。成分替代法是常见的全色锐化方法之一,主要有主成分分析 (PCA)[1],Gram-Schmidt正交化[2],亮度、色调、饱和度 (IHS) 变换[3]等。此类方法通过对多光谱图像进行某种变换,将多光谱图像的空间信息集中于某一通道,然后用空间信息丰富的全色图像进行替换,最后由逆变换得到空间分辨率提升的多光谱图像,但是此类方法较易产生光谱扭曲。针对此问题,后续的****又提出了一些改进的方法[4-5],文献[4]利用互相关系数对PCA进行改进,给出一种自适应PCA方法,并与轮廓波变换结合,未考虑到遥感图像的光谱特征。文献[5]利用粒子群优化给出一种自适应成分替代法,得到自适应的权重系数,未考虑到遥感图像的几何特征。上述方法可以在一定程度上降低光谱误差,但仍未完全克服光谱误差较大的弊端。为进一步减少光谱信息损失,人们开始提出基于多尺度变换的方法,主要有小波变换 (WT)[6-7]、非下采样小波变换 (ATW)[8-10]、拉普拉斯金字塔变换 (LP)[11-12]、曲波变换 (Curvelet)[13]、非下采样轮廓波变换 (NSCT)[14-15]及小波框架变换[16-18]等。此类方法首先将图像从空间域转换到变换域,然后针对变换系数的特点制定相应的融合规则,最后将得到的融合系数进行逆变换得到融合图像。此外,还有****提出其他方法[19-22],文献[19]通过区域地图学习插值进行全色锐化,文献[20]提出基于非局部参数的优化模型,文献[21-22]将稀疏表示与细节注入模型结合。2015年,Vivone等对全色锐化方法进行了总结和比较分析[23]。
Grady将基于图论的随机游走方法应用于图像分割,此方法有助于对边缘轮廓信息的识别,且对弱边缘也有较好的提取效果[24-25]。Shen等将其推广到多曝光图像融合[26],通过随机游走得到每个像素点的到达概率来确定融合权重。Hua等根据多聚焦图像的特点,重新构造随机游走协调函数,将其应用于多聚焦图像融合[27]。
文献[26-27]均是在空间域上建立随机游走融合模型,直接对像素点融合。由于多光谱图像经IHS变换后,其Ⅰ通道仍包含了一部分光谱信息。如果利用随机游走在空间域对多光谱图像的Ⅰ通道与直方图匹配后的全色图像 (与Ⅰ通道具有相同的均值和标准差) 进行融合,虽然可以提高融合图像的空间分辨率,但会产生一定的光谱信息损失。针对此问题,将多光谱图像的Ⅰ通道与匹配后的全色图像变换到框架域进行融合。Ⅰ通道的低频框架系数包含了大部分光谱信息,为保留光谱信息,保持其不变,只对Ⅰ通道和匹配后的全色图像的高频框架系数进行融合。
本文根据高频框架系数主要包含图像边缘轮廓信息的特点,建立基于随机游走的统计融合模型。此模型在构造随机游走协调函数时,考虑到每个高频框架系数的局部统计特征与相关性,又在基于图论的随机游走学习中,考虑到全局的高频框架系数,使得所得融合权重可以较好地度量高频框架系数包含的空间信息,有助于在融合过程中保留图像的边缘轮廓信息,进而提高融合图像的空间分辨率。
1 IHS变换与框架变换 1.1 图像的IHS变换 IHS变换 (式 (1)) 可以将多光谱图像的光谱信息与空间信息进行分离,其中光谱信息主要集中在H、S通道,空间信息主要集中在Ⅰ通道[3]。因此H、S通道保持不变,将匹配后的全色图像与Ⅰ通道进行融合,得到新的Ⅰ通道If,最后由逆IHS变换 (式 (2))[3]得到融合图像。
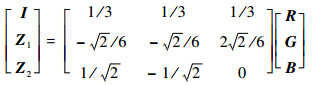 | (1) |
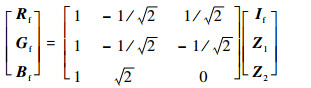 | (2) |
式中:R、G、B为多光谱图像的3个波段;I为多光谱图像的Ⅰ通道;Z1和Z2为2个中间量,H、S通道可由Z1和Z2推导得出,因此保持Z1和Z2不变即可;If为融合图像的Ⅰ通道;Rf、Gf、Bf为融合图像的3个波段。
1.2 图像的框架变换 框架变换相比传统的小波变换具有冗余性且可以实现完全重构,已经有****将其应用在图像融合中[16-18]。由于传统的框架变换不具备平移不变性,因此本文采用非下采样的框架变换,使变换具有平移不变性,且具备更好的冗余性[28]。利用线性B样条框架,通过酉拓展原理 (UEP)[29]得到此框架变换的低通滤波器
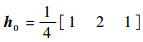
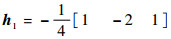
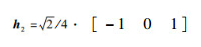
2 随机游走基本原理 本节首先给出基于图论的随机游走,在此基础上,给出随机游走标记问题 (未标记顶点到标记顶点的到达概率) 的求解过程。
由图论,图可由顶点集与边集表示。顶点集为V={vm, m=1, 2, …, K+MN}={Y, X},vm为顶点,Y={Yl, l=1, 2, …, K}为标记顶点集,Yl用来标记K个待融合的系数矩阵,X={xi, i=1, 2, …, MN}为未标记顶点集,可看作MN个随机变量,xi为第i个系数。边集为ε={ei, l1, ei, j2}, i, j=1, 2, …, MN, l=1, 2, …, K, ei, l1为未标记顶点与标记顶点连接形成的边;ei, j2为未标记顶点之间连接形成的边,一般采用四邻域的方法进行连接。本文采用无向图,边ei, l1与ei, j2的权值可记为wi, l1与wi, j2。如无特别说明,文中的上标1,2均表示序号。综上,基于图论的随机游走如图 1所示。
 |
| 图 1 基于图论的随机游走 Fig. 1 Random walk based on graph theory |
| 图选项 |
为得到未标记顶点到标记顶点的到达概率,首先定义顶点间的协调函数为[26]
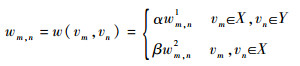 | (3) |
式中:w(vm, vn) 为计算顶点vm与vn之间权值的协调函数,wm, n为其简化表示;wm, n1为第m个未标记顶点与第n个标记顶点之间的权值;wm, n2为第m个未标记顶点与第n个未标记顶点之间的权值;α与β为调节参数,对权值wm, n1与wm, n2进行调节。
由文献[20]可知,标记问题可以转化为求解相应的狄利克雷问题。令u(vm) 表示在点vm处的能量,图 1系统的总能量E为[25]
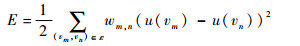 | (4) |
目标是找到满足
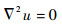
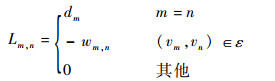 | (5) |
式中:Lm, n为矩阵L在m行n列处的矩阵元素值,L的维数为 (K+MN)×(K+MN);dm为在点vm邻域处的度;wm, n可由式 (3) 计算得到。
式 (4) 可以转化为矩阵表示
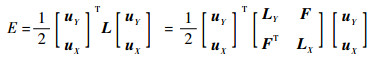 | (6) |
式中:uY和uX分别为标记的矩阵和未标记的矩阵;LY和LX分别为标记顶点间连接的权值矩阵和未标记顶点间连接的权值矩阵;F为未标记顶点与标记顶点间连接的权值矩阵。
最后通过求解
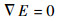
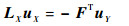 | (7) |
赋值uY,求解式 (7) 得到uX,然后由uX得到未标记顶点到标记顶点的到达概率。
3 高频框架系数的统计融合模型 本节讨论高频框架系数的融合,首先给出统计融合模型:
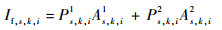 | (8) |
式中:If, s, k, i表示融合后的s尺度、k高频子带的第i个框架系数;As, k, i1与As, k, i2分别表示Ⅰ通道与匹配后的全色图像的s尺度、k高频子带的第i个框架系数;Ps, k, i1与Ps, k, i2分别表示Ⅰ通道与匹配后的全色图像的s尺度、k高频子带的第i个框架系数的融合权重;i=1, 2, …, MN;s=1, 2, …, J,J为分解尺度;k=1, 2, …, 8, 表示8个高频子带。
模型中融合权重Ps, k, i1与Ps, k, i2未知,根据第2节给出的随机游走基本原理,将融合权重Ps, k, i1与Ps, k, i2的计算转化为随机游走标记问题的求解。用标记顶点表示待融合的高频子带,未标记顶点表示高频子带中的每个框架系数。首先给出高频框架系数的统计特性,然后在此基础上重新构造随机游走协调函数,最后转化为求解线性方程组,得到每个高频框架系数与所对应高频子带的概率关系,即每个高频框架系数的融合权重。
3.1 高频框架系数的统计特性 根据文献[30]总结的小波变换特性:聚集性 (clustering) 与持续性 (persistence)。类似得出高频框架系数的统计特性:同一尺度同一子带内的邻域相关性与不同尺度相同子带间的尺度相关性。邻域相关性:如果一个框架系数是大 (小) 的,则其相邻的系数也很可能是大 (小) 的,如图 2(a)所示。尺度相关性:框架系数大 (小) 的属性沿尺度传递,如图 2(b)所示。其中,As, k, i为位于s尺度、k高频子带内第i个框架系数。
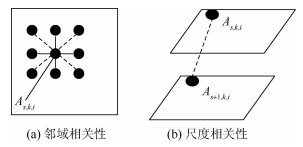 |
| 图 2 高频框架系数的邻域相关性与尺度相关性 Fig. 2 Neighborhood correlation and scale correlation of high frequency framelet coefficients |
| 图选项 |
3.2 基于高频框架系数统计特性的协调函数构造 类比式 (2),定义关于s尺度、k高频子带的协调函数:
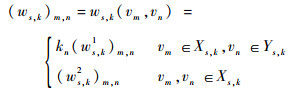 | (9) |
式中:
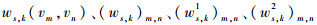
为将 (ws, k1)m, n和 (ws, k2)m, n的下标进行区分,本文用 (ws, k1)i, l表示 (ws, k1)m, n,用 (ws, k2)i, j表示 (ws, k2)m, n。此处i, j=1, 2, …, MN,表示s尺度、k高频子带的第i、j个框架系数;此外,由于本文是对2幅图像进行融合,所以取l=1, 2,分别代表多光谱图像的Ⅰ通道和匹配后的全色图像。
3.2.1 (ws, k1)i, l的构造 本节根据高频框架系数的邻域相关性与尺度相关性构造 (ws, k1)i, l。
由3.1节知,高频框架系数具有邻域相关性,所以对高频框架系数进行度量时,需要考虑其邻域信息 (四邻域或者八邻域,如图 2(a)所示) 的影响。本文先计算每个高频框架系数与其邻域均值的距离,然后再与其邻域的标准差做比值运算,具体计算过程见式 (10)~式 (12)。
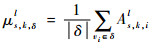 | (10) |
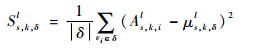 | (11) |
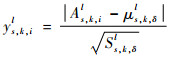 | (12) |
式中:l=1, 2;δ为高频框架系数的邻域,|δ|为邻域包含的系数个数;us, k, δl与Ss, k, δl分别为高频框架系数邻域的均值与方差;ys, k, il为高频框架系数的度量值,ys, k, il越大,表明高频框架系数越显著,包含空间信息越多。
在式 (12) 中,仅考虑了高频框架系数在同一尺度下同一子带内的邻域相关性。由于本文采用多尺度框架变换,所以仍需考虑高频框架系数在不同尺度下的相关性影响。由3.1节知高频框架系数具有尺度相关性,如图 2(b)所示。通过比较ys, k, il的大小以及Ⅰ通道与匹配后的全色图像在不同尺度同一子带间的相关系数对ys, k, il进行修正,具体计算过程见式 (13)~式 (17)。
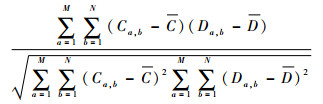 | (13) |
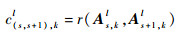 | (14) |
式中:r为计算矩阵C与D的相关系数;Ca, b和Da, b分别为矩阵C与D在a行b列的矩阵元素值;C与D分别为矩阵C与D的均值;l=1, 2;As, k1与As+1, k1分别为Ⅰ通道的s、s+1尺度、k高频子带矩阵,As, k2与As+1, k2同上所述,为匹配后的全色图像;c(s, s+1), k1与c(s, s+1), k2分别为Ⅰ通道与匹配后的全色图像在不同尺度同一子带间的相关系数。
如果ys, k, il < ys+1, k, il,则
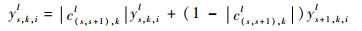 | (15) |
反之,则
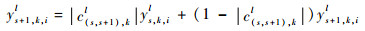 | (16) |
最后对ys, k, il进行归一化处理,得到
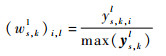 | (17) |
式中:max (ys, kl) 为求向量ys, kl所有元素中的最大值,ys, kl为由元素ys, k, il组成的向量。
3.2.2 (ws, k2)i, j的构造 本节根据高斯函数[21]构造 (ws, k2)i, j:
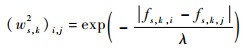 | (18) |
式中:λ取100;i, j=1, 2, …, MN;fs, k, i和fs, k, j表示s尺度、k高频子带的第i、j个系数的度量。
文献[21-22]均采用取均值的方法计算fs, k, i,但本文是在框架域上进行随机游走,需要考虑高频框架系数不同子带间的相关性影响。因此由Ⅰ通道与匹配后的全色图像在同一尺度,相同高频子带间的相关系数计算fs, k, i,具体计算过程见式 (19) 和式 (20),同理可得fs, k, j。
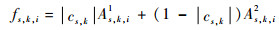 | (19) |
 | (20) |
式中:cs, k为Ⅰ通道与匹配后的全色图像在s尺度、k高频子带间的相关系数。
综上分析,利用式 (9)~式 (20) 可以得到基于高频框架系数统计特性的协调函数 (ws, k)m, n。
3.3 高频框架系数融合权重的求解 本节通过求解随机游走标记问题,得到多光谱图像的Ⅰ通道与匹配后的全色图像的s尺度、k高频子带的融合权重。
本文将3.2节构造的协调函数代入第2节给出的随机游走标记问题的求解过程,将问题转化为线性方程组的求解:
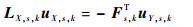 | (21) |
式中:
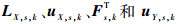
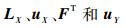
首先类比第2节给出的公式,由协调函数 (ws, k)m, n构造新的拉普拉斯矩阵,进而确定矩阵
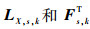
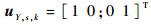
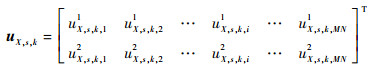 | (22) |
式中:uX, s, k, i1与uX, s, k, i2分别表示第1行和第2行的矩阵元素值。
利用uX, s, k计算Ⅰ通道与匹配后全色图像s尺度、k高频子带的第i个框架系数的融合权重为
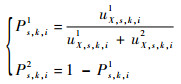 | (23) |
最后将融合权重Ps, k, i1与Ps, k, i2代入式 (8),即可得到融合后的高频框架系数。
3.4 融合算法流程 步骤1?对多光谱图像进行IHS变换 (见式 (1)),得到多光谱图像的Ⅰ通道,并利用Ⅰ通道对全色图像进行直方图匹配,使全色图像与Ⅰ通道具有相同的均值和标准差[17]。
步骤2?利用非下采样框架变换分别对多光谱图像的Ⅰ通道和匹配后的全色图像进行多尺度框架分解,得到低、高频框架系数。
步骤3?框架系数融合。低频:保留多光谱图像的Ⅰ通道的低频框架系数;高频:利用基于随机游走的统计融合模型对多光谱图像的Ⅰ通道和匹配后的全色图像的高频框架系数进行融合 (见式 (8))。
步骤4?对融合后的框架系数进行重构,得到融合全色图像空间信息的新的Ⅰ通道If。
步骤5?用If替换I,进行逆IHS变换 (见式 (2)),得到具有高空间分辨率的多光谱图像。
4 实验与结果分析 4.1 实验数据与评价指标 选取2类常见的遥感卫星拍摄的全色图像与多光谱图像进行图像融合实验:Quick Bird遥感卫星拍摄的Pyramids全色图像 (PY-PAN) 与Pyramids多光谱图像 (PY-MS) 融合;Landsat 7 ETM+遥感卫星拍摄的Wenzhou全色图像 (WZ-PAN) 与Wenzhou多光谱图像 (WZ-MS) 融和。全色图像和多光谱图像如图 3所示。选取的图像大小均为512像素×512像素,利用MATLAB-2012a对选取的图像按照3.4节给出的算法流程进行编程实验。
 |
| 图 3 全色图像与多光谱图像 Fig. 3 Panchromatic images and multispectral images |
| 图选项 |
在客观评价中,从光谱误差与空间分辨率2个角度分析融合效果,采用全色锐化常用的3个评价指标:相对平均光谱误差 (RASE)[31],相对无维全局光谱误差 (ERGAS)[31],空间相关系数 (SCC)[32]。
由文献[31]可知, RASE与ERGAS从光谱误差的角度衡量融合效果,RASE与ERGAS的值越小,表明光谱误差越小,它们的理想值为0,其定义分别为
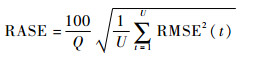 | (24) |
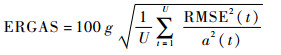 | (25) |
式中:U为波段总数;Q为参考图像所有波段的均值;RMSE (t) 为融合图像与参考图像的第t波段的均方根误差;g为全色图像与多光谱图像的像素大小的比值;a(t) 为参考图像的第t波段的均值。
由文献[32], SCC用来衡量融合图像的空间分辨率,利用拉普拉斯滤波器 (见式 (26)) 提取全色图像与融合后的Ⅰ通道的高频信息,然后计算相关系数,SCC的值越大,表明融合图像的空间分辨率越高,其理想值为1。
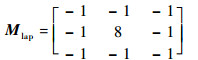 | (26) |
4.2 参数选取
4.2.1 分解尺度J的分析 本节讨论分解尺度J的选取,取k1=k2=1保持不变,J分别取2、3、4进行仿真实验,实验结果见表 1,括号内为评价指标的理想值。
表 1 不同分解尺度的融合结果 Table 1 Fusion results for different decomposition level
| 图像 | J | RASE (0) | ERGAS (0) | SCC (1) |
| PY-PAN+PY-MS4 | 2 | 3.378 8 | 0.845 8 | 0.972 0 |
| 3 | 4.336 5 | 1.084 2 | 0.978 9 | |
| 4 | 5.012 0 | 1.251 5 | 0.979 6 | |
| WZ-PAN+WZ-MS | 2 | 6.176 5 | 3.092 5 | 0.970 6 |
| 3 | 9.135 6 | 4.566 7 | 0.976 9 | |
| 4 | 10.217 4 | 5.106 1 | 0.977 4 |
表选项
由表 1可知,随着分解尺度J的增加,融合图像的空间分辨率提升,但光谱误差增大。在J取2时,融合图像的空间分辨率已经较高,随着J的增加,空间分辨率没有明显提升,又考虑到光谱误差与实验运行时间,所以本文取J为2时进行融合实验。
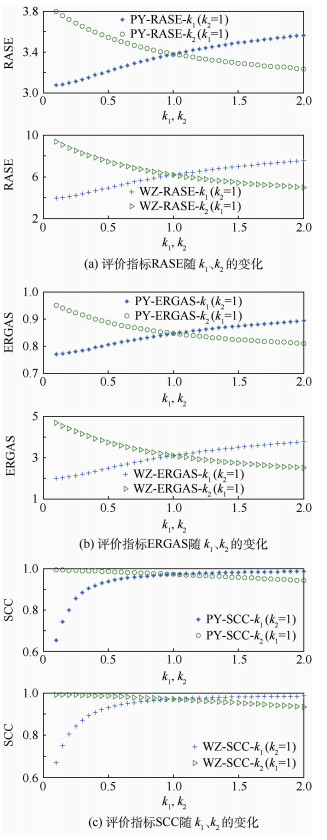
4.2.2 参数kn的分析 由于只对2幅图像融合,所以只需讨论k1与k2变化对融合效果的影响。为分别看其影响,分2种情况进行讨论:固定k2=1,令k1从0.1到2变化,间隔取0.05;固定k1=1,令k2从0.1到2变化,间隔取0.05。按照上述思想,对2类遥感图像进行融合实验。PY图像融合以及WZ图像融合的评价指标随k1与k2变化的曲线图见图 4。
 |
| 图 4 评价指标随k1、k2的变化 Fig. 4 Variation of evaluation indices with k1 and k2 |
| 图选项 |
由图 4可以发现:k2保持不变时,随着k1的增大,融合图像的空间分辨率逐渐提高,但光谱误差逐渐增大;k1保持不变时,随着k2的增大,融合图像的光谱误差逐渐减小,但融合图像的空间分辨率逐渐减小。因此,本文只需固定其中一个参数,令另一个参数变化,即可得到不同情况下的融合图像。由图 4还可以发现:固定k2,而k1变化时,评价指标在初始时波动较大,虽然可以得到较低的光谱误差,但空间分辨率更低,不符合实际需求。所以本文固定k1=1,令k2从0.1到2进行变化,融合实验结果见表 2。
表 2 取不同k2的融合结果 Table 2 Fusion results for different k2
| 图像 | k2 | RASE (0) | ERGAS (0) | SCC (1) |
| PY-PAN+PY-MS | 0.1 | 3.796 0 | 0.950 1 | 0.993 1 |
| 0.5 | 3.544 8 | 0.887 4 | 0.985 3 | |
| 0.9 | 3.403 2 | 0.852 0 | 0.974 9 | |
| 1.0 | 3.378 8 | 0.845 8 | 0.972 0 | |
| 1.1 | 3.358 4 | 0.840 7 | 0.969 2 | |
| 1.5 | 3.289 3 | 0.823 6 | 0.957 2 | |
| 1.9 | 3.243 3 | 0.812 2 | 0.944 8 | |
| 2.0 | 3.232 6 | 0.809 5 | 0.941 7 | |
| WZ-PAN+WZ-MS | 0.1 | 9.374 3 | 4.686 2 | 0.991 8 |
| 0.5 | 7.468 1 | 3.735 7 | 0.985 1 | |
| 0.9 | 6.377 2 | 3.192 3 | 0.973 8 | |
| 1.0 | 6.176 5 | 3.092 5 | 0.970 6 | |
| 1.1 | 5.996 6 | 3.003 0 | 0.967 3 | |
| 1.5 | 5.439 3 | 2.725 9 | 0.953 0 | |
| 1.9 | 5.062 7 | 2.538 8 | 0.938 1 | |
| 2.0 | 4.986 7 | 2.501 1 | 0.934 3 |
表选项
由表 2可知,当k1为1,k2大于1时,融合图像的空间分辨率变得较低,不符合实际需求。因此k1为1,k2的范围在0与1之间时,可以在空间分辨率与光谱误差之间达到较好的平衡。
4.3 与其他全色锐化方法的比较 本节将基于框架域的随机游走全色锐化方法 (NFT+RW) 与基于空间域的随机游走融合方法 (RW)[27]及其他8种主流全色锐化方法做比较,包括:Gram-Schmidt正交化法 (GS)[2]、IHS变换法 (IHS)[3]、基于广义金字塔变换与调制传递函数的方法 (MTF+GLP)[12]、基于非下采样小波变换的上下文驱动融合方法 (AWT+CDWL)[9]、光谱误差最小注入方法 (AWT+SDM)[10]、基于非下采样轮廓波变换的图像融合方法 (NSCT)[14]、基于不可分离框架提升变换的协方差交叉融合方法 (NFLT+CI)[17]以及基于稀疏表示与细节注入模型的全色锐化方法 (SRDIP)[22]。
用上述全色锐化方法对2类图像:PY-MS与PY-PAN以及WZ-MS与WZ-PAN进行融合实验,其中本文方法的参数k2取3种情况:k2=0.1,0.5,0.9。从客观评价指标和主观融合效果2个角度对比分析,客观评价指标见表 3,融合图像见图 5,分别用PY-FUS与WZ-FUS表示融合后的图像。
 |
| 图 5 融合图像 Fig. 5 Fusion images |
| 图选项 |
表 3 不同融合方法的融合结果 Table 3 Fusion results of different fusion methods
| 图像 | 融合方法 | RASE (0) | ERGAS (0) | SCC (1) |
| PY-PAN+PY-MS | GS | 14.453 6 | 3.626 0 | 0.998 8 |
| IHS | 13.193 0 | 3.272 8 | 0.999 6 | |
| MTF+GLP | 3.950 3 | 0.990 7 | 0.966 1 | |
| AWT+CDWL | 4.964 8 | 1.237 3 | 0.903 9 | |
| AWT+SDM | 6.793 1 | 1.695 0 | 0.993 9 | |
| NSCT | 7.863 2 | 1.995 9 | 0.999 0 | |
| NFLT+CI | 3.959 7 | 0.990 7 | 0.960 0 | |
| SRDIP | 3.742 8 | 0.935 3 | 0.948 0 | |
| RW | 9.485 9 | 2.355 0 | 0.986 5 | |
| NFT+RW (k2=0.1) | 3.796 0 | 0.950 1 | 0.993 1 | |
| NFT+RW (k2=0.5) | 3.544 8 | 0.887 4 | 0.985 3 | |
| NFT+RW (k2=0.9) | 3.403 2 | 0.852 0 | 0.974 9 | |
| WZ-PAN+WZ-MS | GS | 32.363 8 | 16.231 3 | 0.990 1 |
| IHS | 33.678 2 | 16.822 8 | 0.999 5 | |
| MTF+GLP | 6.440 0 | 3.232 3 | 0.868 9 | |
| AWT+CDWL | 13.256 7 | 6.614 3 | 0.931 9 | |
| AWT+SDM | 18.870 9 | 9.419 8 | 0.949 8 | |
| NSCT | 16.173 3 | 8.102 5 | 0.996 6 | |
| NFLT+CI | 6.437 4 | 3.223 8 | 0.956 3 | |
| SRDIP | 7.792 3 | 3.891 6 | 0.943 9 | |
| RW | 21.363 4 | 10.672 8 | 0.982 4 | |
| NFT+RW (k2=0.1) | 9.374 3 | 4.686 2 | 0.991 8 | |
| NFT+RW (k2=0.5) | 7.468 1 | 3.735 7 | 0.985 1 | |
| NFT+RW (k2=0.9) | 6.377 2 | 3.192 3 | 0.973 8 |
表选项
由表 3,从客观评价指标分析。首先在2类图像融合中,NFT+RW方法均可得到比传统的RW方法更优的评价指标值。其次,GS与IHS方法虽然可以得到较高的SCC值,但其RASE与ERGAS值过大。这表明,成分替代法虽然可以大幅提高融合图像的空间分辨率,但会造成较大的光谱误差。在基于多尺度变换的方法中,分析PY图像融合:NFT+RW方法的评价指标值优于MTF+GLP、AWT+CDWL和NFLT+CI方法。虽然NSCT与AWT+SDM方法的SCC值略高于NFT+RW方法,但其RASE、ERGAS值远大于NFT+RW方法;同样分析WZ图像融合:NFT+RW方法的评价指标值优于MTF+GLP、AWT+SDM AWT+CDWL、和NFLT+CI方法。虽然NSCT方法的SCC值略高于NFT+RW方法,但其RASE、ERGAS值是NFT+RW方法的2倍左右,即光谱误差远大于NFT+RW方法。此外,NFT+RW方法在2类图像融合中的评价指标值均优于SRDIP方法。综上,权衡空间分辨率与光谱误差的评价指标值,NFT+RW方法可以在保持光谱误差较低的情况下,使融合图像空间分辨率提高,优于传统的RW方法和其他全色锐化方法。
由图 5,从主观融合效果分析。首先可以发现在2类图像融合中,成分替代法GS与IHS以及传统的RW方法都会产生光谱扭曲现象。然后,观察基于多尺度变换的融合图像:在PY图像融合中,本文方法所得融合图像的边缘轮廓比MTF+GLP、AWT+CDWL和NFLT+CI方法清晰且光谱特性保持得更好。虽然NSCT与AWT+SDM方法所得融合图像的边缘轮廓的清晰度略优于NFT+RW方法,但其融合图像在草地区域发生较大的光谱扭曲;在WZ图像融合中,与NFT+RW方法相比,AWT+CDWL、AWT+SDM、NSCT方法仍有较明显的光谱扭曲现象。虽然MTF+GLP、NFLT+CI和SRDIP方法在光谱特性保持方面与NFT+RW方法接近,但其边缘轮廓不如NFT+RW方法清晰。综上,权衡融合图像的光谱特性与空间分辨率,NFT+RW方法在主观融合效果上也优于传统的RW方法和其他全色锐化方法。
4.4 计算复杂度 假设图像的像素个数为MN,框架变换的分解尺度为J,则算法中IHS变换的计算复杂度为O (MN),直方图匹配的计算复杂度为O (MN),非下采样框架变换的计算复杂度为O (JMN),协调函数构造的计算复杂度为O (JMN),稀疏线性方程组求解采用共轭梯度平方法[33],其计算复杂度与稀疏矩阵非零元的个数与以及迭代次数Iter有关,为O (IterJMN)。综上,本文方法的计算复杂度与图像大小、分解次数以及迭代次数有关。为与其他方法进行比较,本文统一利用MATLAB在3.4 GHz主频与8 GB内存的电脑环境下运行不同全色锐化方法的程序,得到运行时间见表 4。由表 4可知,本文方法的运行时间为7 s左右,优于MTF+GLP与SRDIP方法。又因为本文方法基于框架域进行分析,并在框架系数融合中考虑到每个框架系数的局部统计特征,在得到较好结果的同时,增加了一定的计算复杂度,与GS、IHS和AWT等方法相比,运行时间相对较长,可以用并行计算进行加速。综上,本文方法的计算复杂度适中,并由4.3节知,相比计算简单的方法,其融合结果更好。
表 4 不同融合方法的运行时间 Table 4 Elapsed time of different fusion methodss
| 融合方法 | PY图像融合 | WZ图像融合 |
| GS | 0.195 6 | 0.232 6 |
| IHS | 0.114 3 | 0.117 6 |
| MTF+GLP | 73.718 5 | 72.531 1 |
| AWT+CDWL | 0.835 5 | 0.877 4 |
| AWT+SDM | 0.718 5 | 0.779 5 |
| NSCT | 4.854 4 | 4.873 6 |
| NFLT+CI | 0.557 0 | 0.394 8 |
| SRDIP | 1 243.125 6 | 1 306.896 6 |
| RW | 1.652 0 | 1.666 5 |
| NFT+RW (k2=0.1) | 7.513 5 | 7.232 2 |
| NFT+RW (k2=0.5) | 7.510 9 | 7.254 2 |
| NFT+RW (k2=0.9) | 7.530 1 | 7.375 4 |
表选项
5 结论 1) 提出一种基于框架域的随机游走全色锐化方法。在低频融合中,为保留光谱信息,保持多光谱图像Ⅰ通道的低频框架系数不变;在高频融合中,为提高空间分辨率,建立基于随机游走的统计融合模型。该模型根据高频框架系数的统计特性,重新构造随机游走协调函数,通过求解框架域上的随机游走标记问题得到高频框架系数的融合权重。
2) 在实验中,利用新给出的全色锐化方法对2类遥感图像进行融合,并与8种主流全色锐化方法以及基于空间域的随机游走融合方法比较。从客观评价指标与主观融合效果2个方面可知本文方法可以在光谱误差减小与空间分辨率提高之间达到较好的平衡,并且有利于保持边缘轮廓的清晰,避免光谱扭曲现象。
参考文献
| [1] | CHAVEZ P S, SIDES J S C, ANDERSON J A. Comparison of three different methods to merge multiresolution and multispectral data Landsat TM and SPOT panchromatic[J].Photogrammetric Engineering and Remote Sensing, 1991, 57(3): 265–303. |
| [2] | LABEN C A, BROWER B V.Process for enhancing the spatial resolution of multispectral imagery using pan-sharpening:US 6011875 A[P].2000-04-01. |
| [3] | TU T M, SU S C, SHYU H C, et al. A new look at IHS-like image fusion methods[J].Information Fusion, 2001, 2(3): 177–186.DOI:10.1016/S1566-2535(01)00036-7 |
| [4] | SHAH V P, YOUNAN N H, KING R L. An efficient pan-sharpening method via a combined adaptive PCA approach and contourlets[J].IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(5): 1323–1335.DOI:10.1109/TGRS.2008.916211 |
| [5] | WANG W, JIAO L, YANG S. Novel adaptive component substitution based pan-sharpening using particle swarm optimization[J].IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 781–785.DOI:10.1109/LGRS.2014.2361834 |
| [6] | ZHOU J, CIVCO D L, SILANDER J A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data[J].International Journal of Remote Sensing, 1998, 19(4): 743–757.DOI:10.1080/014311698215973 |
| [7] | 袁晓冬, 李超, 盛浩. 小波多分辨分量相关性图像融合方法[J].北京航空航天大学学报, 2013, 39(6): 847–852. YUAN X D, LI C, SHENG H. Wavelet multi resolution weight correlation image fusion method[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(6): 847–852.(in Chinese) |
| [8] | NUNEZ J, OTAZU X, FORS O, et al. Multiresolution based image fusion with additive wavelet decomposition[J].IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(3): 1204–1211.DOI:10.1109/36.763274 |
| [9] | GARZELLI A, BENELLI G, BARNI M, et al. Improving wavelet based merging of panchromatic and multispectral images by contextual information[J].Proceedings of SPIE-The International Society for Optical Engineering, 2001, 4170: 82–91. |
| [10] | GARZELLI A, NENCINI F. Interband structure modeling for Pan-sharpening of very high-resolution multispectral images[J].Information Fusion, 2005, 6(3): 213–224.DOI:10.1016/j.inffus.2004.06.008 |
| [11] | AIAZZI B, ALPARONE L, BARONTI S, et al. Context driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(10): 2300–2312.DOI:10.1109/TGRS.2002.803623 |
| [12] | AIAZZI B, AIPARONE L, BARONTI S, et al. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery[J].Photogrammetric Engineering and Remote Sensing, 2006, 72(5): 591–596.DOI:10.14358/PERS.72.5.591 |
| [13] | CHOI M, KIM R Y, NAM M R, et al. Fusion of multispectral and panchromatic satellite images using the curvelet transform[J].IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 136–140.DOI:10.1109/LGRS.2005.845313 |
| [14] | 贾建, 焦李成, 孙强. 基于非下采样Contourlet变换的多传感器图像融合[J].电子学报, 2007, 35(10): 1934–1938. JIA J, JIAO L C, SUN Q. The nonsubsampled contourlet transform in multisensory images fusion[J].Acta Electronica Sinica, 2007, 35(10): 1934–1938.DOI:10.3321/j.issn:0372-2112.2007.10.022(in Chinese) |
| [15] | 陶旭婷, 和红杰, 陈帆, 等. 基于局部相关性的遥感图像全色锐化算法[J].光子学报, 2014, 43(3): 310003-1–310003-6. TAO X T, HE H J, CHEN F, et al. Pan-sharpening algorithm for remote sensing images based on local correlation[J].Acta Photonica Sinica, 2014, 43(3): 310003-1–310003-6.(in Chinese) |
| [16] | LI S, KWOK J T, WANG Y. Using the discrete wavelet frame transform to merge Landsat TM and SPOT panchromatic images[J].Information Fusion, 2002, 3(1): 17–23.DOI:10.1016/S1566-2535(01)00037-9 |
| [17] | SHI Y, YANG X Y, CHENG T. Pansharpening of multispectral images using the nonseparable framelet lifting transform with high vanishing moments[J].Information Fusion, 2014, 20(1): 213–224. |
| [18] | FANG F, ZHANG G, LI F, et al. Framelet based pan-sharpening via a variational method[J].Neurocomputing, 2014, 129(1): 362–377. |
| [19] | SHI C, LIU F, LI L, et al. Learning interpolation via regional map for pan-sharpening[J].IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3417–3431.DOI:10.1109/TGRS.2014.2375931 |
| [20] | GARZELLI A. Pansharpening of multispectral images based on nonlocal parameter optimization[J].IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2096–2107.DOI:10.1109/TGRS.2014.2354471 |
| [21] | VICINANZA M R, RESTAINO R, VIVONE G, et al. A pansharpening method based on the sparse representation of injected details[J].IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 180–184.DOI:10.1109/LGRS.2014.2331291 |
| [22] | YIN H T. Sparse representation based pansharpening with details injection model[J].Signal Processing, 2015, 113: 218–227.DOI:10.1016/j.sigpro.2014.12.017 |
| [23] | VIVONE G, ALPARONE L, CHANUSSOT J, et al. A critical comparison among pansharpening algorithms[J].IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2565–2586.DOI:10.1109/TGRS.2014.2361734 |
| [24] | GRADY L.Multilabel random walker image segmentation using prior models[C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2005:763-770. |
| [25] | GRADY L. Random walks for image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(11): 1768–1783.DOI:10.1109/TPAMI.2006.233 |
| [26] | SHEN R, CHENG I, SHI J, et al. Generalized random walks for fusion of multi-exposure images[J].IEEE Transactions on Image Processing, 2011, 20(12): 3634–3646.DOI:10.1109/TIP.2011.2150235 |
| [27] | HUA K L, WANG H C, RUSDI A H, et al. A novel multi-focus image fusion algorithm based on random walks[J].Journal of Visual Communication and Image Representation, 2014, 25(5): 951–962.DOI:10.1016/j.jvcir.2014.02.009 |
| [28] | SHI Y, YANG X Y, GUO Y H. Translation invariant directional framelet transform combined with gabor filters for image denoising[J].IEEE Transactions on Image Processing, 2014, 23(1): 44–55.DOI:10.1109/TIP.2013.2285595 |
| [29] | DAUBECHIES I, HAN B, RON A, et al. Framelets:MRA-based constructions of wavelet frames[J].Applied and Computational Harmonic Analysis, 2003, 14(1): 1–46.DOI:10.1016/S1063-5203(02)00511-0 |
| [30] | CROUSE M S, NOWAK R D, BARANIUK R G. Wavelet-based statistical signal processing using hidden Markov models[J].IEEE Transactions on Signal Processing, 1998, 46(4): 886–902.DOI:10.1109/78.668544 |
| [31] | WALD L.Quality of high resolution synthesised images:Is there a simple criterion?[C]//Procedings of the third Conference "Fusion of Earth Data:Merging Point Measurements, Raster Maps and Remotely Sensed Images".[S.l.]:SEE/URISCA, 2000:99-103. |
| [32] | OTAZU X, GONZALEZ-AUDICANA M, FORS O, et al. Introduction of sensor spectral response into image fusion methods[J].IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(10): 2376–2385.DOI:10.1109/TGRS.2005.856106 |
| [33] | SONNEVELD P. CGS, a fast lanczos-type solver for nonsymmetric linear systems[J].SIAM Journal on Scientific and Statistical Computing, 1989, 10(1): 36–52.DOI:10.1137/0910004 |
