文献[3-4]基于马尔可夫过程和更新方程对系统可用度的模型进行了研究。文献[5-8]利用拉氏变换和逆变换的方法各研究了一类特殊系统的瞬时可用度模型。对于复杂可修系统故障时间或维修时间不服从指数分布的系统的可用度分析, 一般借助仿真技术来实现[6, 9]。文献[10]设计了评估复杂可修系统可靠度、瞬时可用度的蒙特卡罗方法,该方法利用Bootstrap方法作为框架,评估得到一个维修周期的非马尔可夫系统的可靠度和瞬时可用度。可以看出瞬时可用度数学模型的建模方法研究工作比较成熟,国内外****对各种复杂的系统建立了较为完善的瞬时可用度方程 (微分、偏微分或积分方程),但这些模型大都直接用于研究稳态可用度是否存在或求解稳态可用度。对于瞬时可用度的求解大多数只能给出故障时间、修复时间服从指数分布、均匀分布或者威布尔分布的某种单一分布形式,不能反映真实保障系统的复杂性、结构性、拓扑性和逻辑性。另外对保障系统的资源等待、备件延误时间等要素考虑不是很充分。
对于瞬时可用度波动研究方面:文献[11-15]运用泛函分析方法,从数学上较为严格地证明了多种类型的可修复系统的瞬时可用度,当时间趋于无穷大时,是稳定的或渐近稳定的;文献[16]对威布尔分布条件下离散时间的单部件可修系统的瞬时可用度模型进行了研究,提出了刻画系统瞬时可用度波动特征的波动参数。这些结论为稳态可用度的研究和应用奠定了坚实的理论基础。然而,军用飞机是一种复杂的可修装备,工程上的现实需求关心的问题是其使用瞬时可用度表现出的波动特性的影响因素是什么?比如在某一特定使用环境、基于不同任务驱动的情况下某一时间段的可用度波动情况如何?因此研究军用飞机在任务准备期内的瞬时可用度是工程上急需的重要基础理论问题。
本文通过对使用任务要求和装备技术状态分析建立随机维修网络 (SMTN),通过定义、求解SMTN的矩母函数和传递函数,基于蒙特卡罗仿真技术设计了一种新方法来计算随机网络工期函数的数字特征,该方法可以真实地反映军用飞机维修保障过程的逻辑性、拓扑性、结构性和随机性。然后将得到的数字特征代入3种不同分布形式比较选定系统的维修度函数的分布形式,并在任务准备期内对装备的可用度仿真,刻画出在任务准备期内装备瞬时可用度的波动规律,从而为装备的使用决策提供依据、为保障系统的保障效能评估提供量化指标,该模型可以广泛应用到各种复杂的可修系统,是对装备综合保障理论在工程中“动态”指标研究的有力探索。
1 SMTN的构建及分析 1.1 SMTN的构建 项目计划评审技术 (PERT) 是比较盛行的生产管理的科学方法,在流程优化等许多领域得到了广泛应用。从图形表达来看,PERT网是一种由节点与弧组成的有向图,可用于不确定性项目时间的预测,解决项目活动逻辑关系确定、活动持续时间不确定的项目工期问题,其基本形式见图 1。
 |
| 图 1 保障网络示意图 Fig. 1 Schematic diagram of support network |
| 图选项 |
图中:节点用圆圈表示,表示一项保障工作开始或者结束的瞬间,也就是说,节点有2种,一种是工作的开始节点,指保障工作开始的节点 (i);另一种是工作的结束节点,指保障工作结束的节点 (j)。除整个保障流程的开始节点和结束节点以外,其他节点既可以作为工作的开始节点,也可以作为工作的结束节点。箭线表示一项具体的保障工作以及保障工作之间的相互关系,可以在箭线上标注具体的保障工作名称和工作持续时间,实工作 (需要消耗时间的工作) 用“→”表示,虚工作 (不需要消耗时间的工作) 用“
综合考虑军用飞机在任务准备期内涉及的保障资源、保障组织和保障流程的约束,根据保障活动间确定型邻接逻辑关系,采用PERT技术建立维修保障工作的SMTN,并且假设各项活动的持续时间主要受维修保障时间、资源等待时间和备件延误时间等要素的影响,基本思路见图 2。
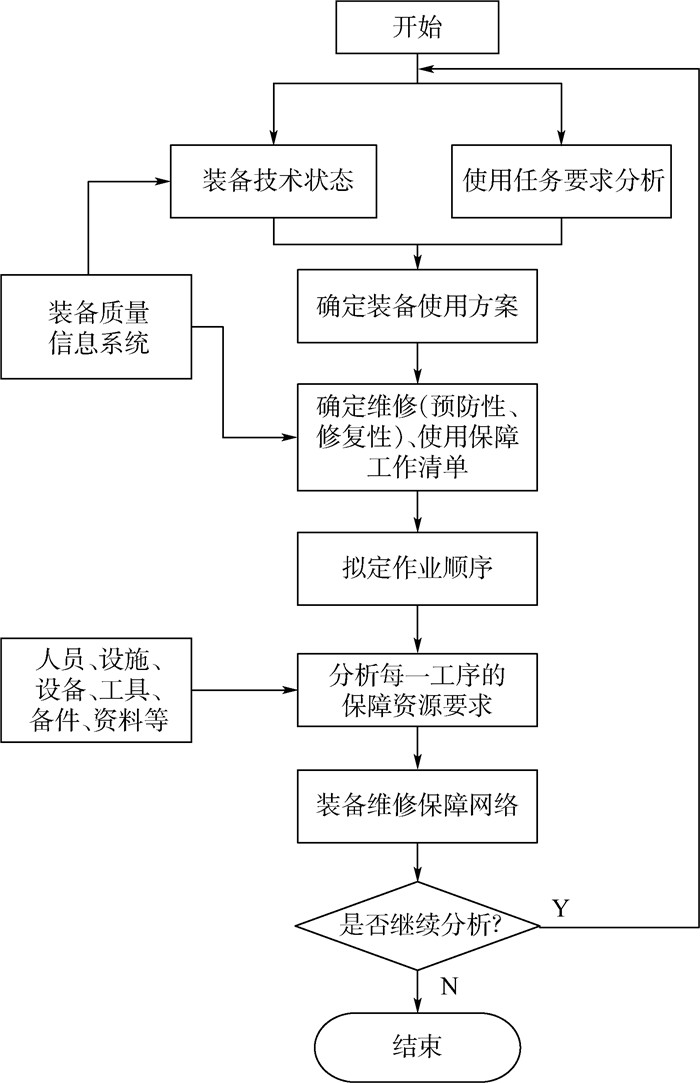 |
| 图 2 军用飞机随机维修网络的确定过程 Fig. 2 Military aircraft SMTN's establishing process |
| 图选项 |
1.2 保障活动持续时间分析 设Tij为图 1中活动从i→j的工期持续时间,Tij=Mij(t)+max (TDi, TWi),Mij(t) 为活动i→j的维修度函数,TWi为活动i→j资源组等待时间,TDi为活动i→j中更换备件引起的延误时间。
维修度函数Mij(t) 为在规定的时间内完成产品维修和保障的概率的时间分布,由于维修产品损坏程度和故障性质不同,在相同的约束条件下,维修时间是随机分布的。文献[17]对常用的分布形式和适用规律进行了归纳,具体如表 1所示。
表 1 常用维修度函数分布形式 Table 1 Classic distribution function of maintainability
| 分布类型 | 维修密度函数 | 函数说明 |
| 指数分布 | 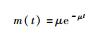 | 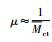 为维修率, 为维修率,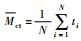 ,Mct为平均维修时间;ti为部件i的维修时间;N为样本观测数量,适用短时间修复或迅速换件的产品 ,Mct为平均维修时间;ti为部件i的维修时间;N为样本观测数量,适用短时间修复或迅速换件的产品 |
| 正态分布 | 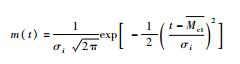 | 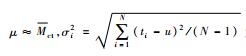 为维修时间的标准方差的平方,适用于故障简单、单一产品的维修活动或基本作业 为维修时间的标准方差的平方,适用于故障简单、单一产品的维修活动或基本作业 |
| 对数正态分布 | 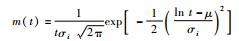 | 适用于修理频率和修理延续时间都互不相等的若干活动组成的复杂装备维修任务 |
表选项
在保障过程中,备件延误时间TDi主要和备件失效率、平均保障率、周转时间等因素相关,其计算方法为
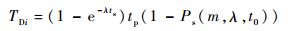 | (1) |
式中:ts为任务持续时间;Ps(m, λ, t0) 为平均备件保障率,m为现场备件数量,t0为补充备件周期中累计的工作时间,λ为部件的失效率;tp为当现场缺少备件时,得到备件的周转时间。
资源组等待时间TWi主要是指在装备维修或者保障过程中,由于维修装备、设施或者器材等因素的约束不能及时开展保障活动而产生的等待时间[18],其计算方法为
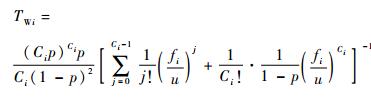 | (2) |
式中:A (k)={A1, A2, …, An (k)}为站点ek内的维修保障活动An (k)的集合,n(k)为ek内保障活动的数量, e1, e2, …, en为保障系统内的n个保障站点;f (k)={f1, f2, …, fn (k)}为站点ei内维修活动的频率的集合,fi为维修保障活动Ai的频率;站点ek内能同时开展的保障活动Ai数量为Ci;p为资源组的平均利用率;u为资源组的平均占用率,其值等于资源组平均占用时间的倒数。
2 基于SMTN的系统维修度函数建模 对于飞机这种复杂的维修系统,其在某一时刻可能需要对多部件进行维修,而且部件的维修度函数分布类型也不尽相同,各项维修工作之间存在逻辑关系,整个系统的维修度函数的分布形式是难以确定的。文献[19-21]通过计算随机网络的矩母函数和传递函数,估算了维修系统的维修度函数的期望和方差。计算过程中不仅要确定网络中各个节点维修度函数的分布形式、特征参数、矩母函数和节点之间活动发生的概率,还要计算各条路径的等价传递函数,计算量比较大,尤其各活动间的概率是比较难确定的。针对该问题基于蒙特卡罗技术设计了一种新方法,具体采用以下思路:
第1步?定义网络的工期矩母函数和传递函数。
定义1?定义M (s) 为某随机变量t的工期矩母函数,s为拉氏算子。
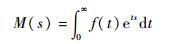 | (3) |
式中:f (t) 为工期的密度函数。
定义2?定义Wij(s) 为活动i→j传递函数。
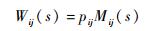 | (4) |
式中:pij为活动i→j可以实现的概率。
第2步?随机网络的工期数字特征计算。
步骤1?根据任务需求和装备的技术状态确定装备保障活动清单。
步骤2?根据保障活动间的逻辑关系建立保障网络。
步骤3?确定网络各项保障活动基本参数:维修活动的概率分布类型及其参数;是否更换备件、备件延误时间计算;是否需要专用或者特种装备,资源组的等待时间计算。
步骤4?基于蒙特卡罗方法仿真,确定关键路径。
步骤5?确定关键路径, 添加一条路径,形成网络闭环。
步骤6?根据梅森拓扑公式计算网络的等价传递函数和矩母函数。
步骤7?求
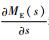
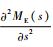
第3步?将计算得到E (t) 和方差σ代入3种分布进行验证,确定系统维修度函数的分布形式,进而计算系统在任务准备内的可用特性。
3 示例分析 假设某次任务准备期时间为2 h 20 min,飞机需要进行的维修保障工作包括:更换前起落架、左发燃油滤、右发启动电机以及机务准备。此次维修保障活动的随机网络可如图 3所示。
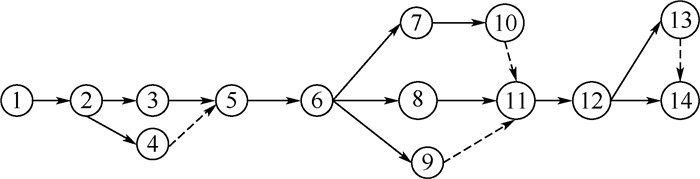 |
| 图 3 军用飞机任务准备期内的随机维修网络 Fig. 3 Military aircraft SMTN during mission preparation period |
| 图选项 |
图 3中共有14个节点,17项活动,各项活动的分布参数如表 2所示,表 2中,μi和σi采用表 1中的方法计算得出;TDi和TWi根据保障系统保障资源的配置情况和统计数据按照式 (1) 和式 (2) 进行计算;“—”表示没有资源等待时间或者延误时间。表 2中数据由飞机使用过程的质量控制信息系统查询得到,如图 4所示。
表 2 各项保障活动的分布函数及参数 Table 2 Distribution function and parameter of support activities
| 活动代号 | 名称 | M (t) | TDi/min | TWi/min | ||
| 分布类型 | μi | σi | ||||
| 1-2 | 更换起落架 | 正态 | 43.5 | 7.41 | 12 | 9 |
| 2-3 | 更换燃油滤 | 正态 | 14.7 | 1.94 | 5 | 5 |
| 2-4 | 启动发电机更换 | 正态 | 9.7 | 1.03 | 4 | 3 |
| 3-5 | 外观检查 | 指数 | 8.41 | — | — | — |
| 4-5 | — | — | — | — | — | — |
| 5-6 | 飞行前准备 | 指数 | 15.03 | — | — | — |
| 6-7 | 补充冷气 | 指数 | 6.01 | — | ||
| 6-8 | 安装阻力伞 | 指数 | 6.52 | — | — | — |
| 6-9 | 补加燃油 | 指数 | 5.21 | — | — | — |
| 7-10 | 补充附油 | 指数 | 3.31 | — | — | — |
| 8-11 | 复查座舱和进排气装置 | 指数 | 6.00 | — | — | — |
| 9-11 | — | — | — | — | — | — |
| 10-11 | — | — | — | — | — | — |
| 11-12 | 组织装挂武器 | 指数 | 15.50 | — | — | — |
| 12-13 | 填写工作日记 | 指数 | 3.56 | — | — | — |
| 12-14 | 清点工具 | 指数 | 3.2 | — | — | — |
| 13-14 | — | — | — | — | — | — |
表选项
 |
| 图 4 飞机装备质量信息控制系统 Fig. 4 Aircraft equipment quality information control system |
| 图选项 |
装备质量信息系统是装备在使用过程中,对装备使用时间、故障信息、维修时间和设备设施等信息综合管理的信息系统,可以为本文的数据采集工作提供有力支撑。
采用蒙特卡罗方法计算出关键路径概率最高的路径为1-2-3-5-6-8-11-12-14。TDi和TWi可以计算得出,所以在计算过程按照常数处理,变量只考虑工期的维修度函数,关键路径上工期持续时间为
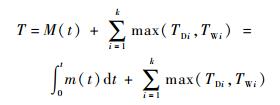 | (5) |
式中:m (t) 为系统的维修密度函数,其分布形式未知。对图 3所示网络添加一条回路,使其构成闭环,如图 5所示。
 |
| 图 5 等价网络 Fig. 5 Equivalent net |
| 图选项 |
采用梅森拓扑公式可得
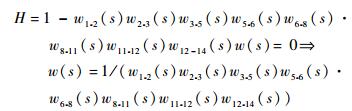 | (6) |
式中:H为网络传递量;w (s) 为网络传递函数。各个工期的矩母函数由式 (3) 计算,各工期pij≡1,则w1-2=eμ1s+0.5σ12s2,w2-3=eμ2s+0.5σ22s2,w3-5=
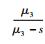
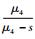
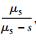
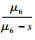
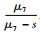
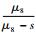
从而得到
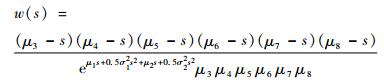 | (7) |
网络的开始时态到结束时态的等价矩母函数为ME(s)=WE(s)=1/w (s),根据矩母函数的性质,得出E (t)=
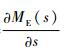
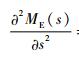
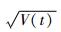
分别假设系统维修度函数服从对数正态分布、正态分布和指数分布,将以上计算结果代入对应的分布函数,采用MATLAB10.0软件对其进行仿真,结果如图 6所示。由于在准备期内装备不发生故障,所以系统的可用度曲线等价于维修度函数曲线。图 6中,曲线1代表对数正态分布, 曲线2代表正态分布, 曲线3代表指数分布。图 6中横坐标对应维修保障时间,纵坐标对应装备的瞬时可用度,随着任务时间的增加维修活动完成的概率不断增加,当t=106 min时,曲线1和2对应的值为0.5,说明了仿真结果的正确性。另外分别计算3种分布函数在时间80 min和123 min之间的完成维修保障活动的概率为0.053 1、0.602 6、0.156 8,正态分布曲线在此区间概率最高,比较符合本次维修过程的实际情况,所以选定正态分布曲线为本次维修度函数的分布形式。从图 6中可以看出,装备的可用度随着时间的变化如曲线2所示,在少于80 min时装备可用度比较低不到0.2,当保障时间到达106 min时,装备的可用度达到0.5,到达140 min时接近0.92,分析可知装备可用度在接近E (t)±σ的区间内,可用度迅速提高。由于任务准备时间为140 min,延误时间和等待时间为17 min,所以可用维修时间为123 min。采用MATLAB软件对任务准备期内装备的可用度计算如图 7所示,装备可用度可以达到0.751 74。
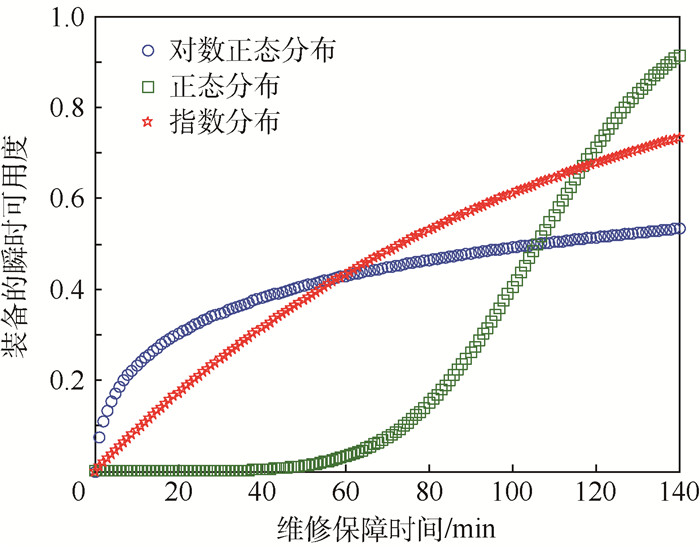 |
| 图 6 不同分布的飞机瞬时可用度 Fig. 6 Instantaneous availability of aircraft with different distributions |
| 图选项 |
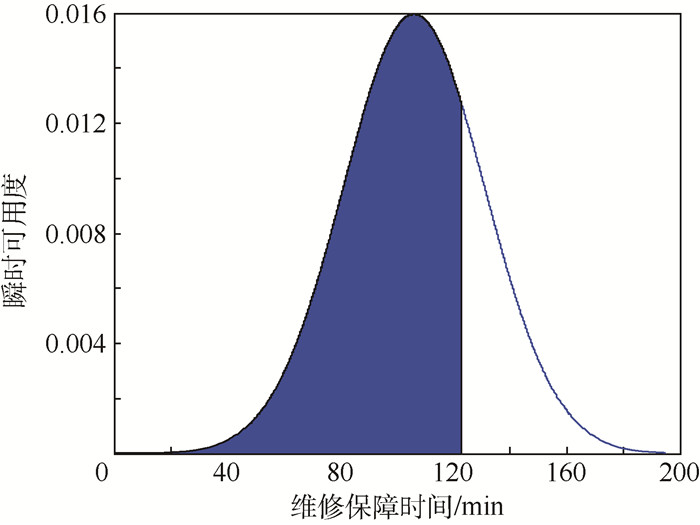 |
| 图 7 任务准备期内飞机的瞬时可用度 Fig. 7 Instantaneous availability of aircraft during mission preparation period |
| 图选项 |
4 结论 1) 构建了基于使用任务和系统技术状态驱动的SMTN,利用网络矩母函数和等价传递函数计算系统维修度函数的数字特征,将计算得到的数字特征代入3种不同分布形式比较,选定正态分布函数为此次维修保障系统的维修时间分布函数,并在任务准备期内对装备的可用度仿真。
2) 在考虑备件延误和资源等待的情况下,任务准备期结束时装备可用度达到0.75以上。计算过程中设计了一种蒙特卡罗方法的等价矩母函数求解方法,在提高了计算效率的同时,可以真实的反映军用飞机的维修保障过程的逻辑性和随机性以及维修网络的结构拓扑特点。
3) 仿真结果可以刻画出在任务准备期内装备瞬时可用度的波动规律,从而为装备的使用决策提供依据,为保障系统的保障效能评估提供量化指标,在装备综合保障领域该模型可以广泛应用到各种复杂的可修系统,是对装备综合保障理论在工程中“动态”指标研究的有力探索。
参考文献
| [1] | 康锐, 王自立. 可靠性系统工程的理论与技术框架[J].航空学报, 2005, 26(5): 633–636. KANG R, WANG Z L. Framework of theory and technique about reliability system engineering[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(5): 633–636.(in Chinese) |
| [2] | 杨懿, 任思超, 于永利. 均匀分布下系统瞬时可用度理论分析[J].北京航空航天大学学报, 2016, 42(1): 28–34. YANG Y, REN S C, YU Y L. Theory analysis of system instantaneous availability under uniform distribution[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 28–34.(in Chinese) |
| [3] | 孔德良, 王少萍. 可修系统的可用度分析方法研究[J].北京航空航天大学学报, 2002, 28(2): 129–132. KONG D L, WANG S P. Study on availability analysis for repairable system[J].Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(2): 129–132.(in Chinese) |
| [4] | MI J. Limiting availability of system with non-identical lifetime distributions and non-identical repair time distributions[J].Statistics & Probability Letters, 2006, 76(7): 729–736. |
| [5] | BRIS R, CHATELET E, YALAOUI E. New method to minimize the preventive maintenance cost of series-parallel systems[J].Reliability Engineering & System Safety, 2003, 82(3): 247–255. |
| [6] | LISNIANSKI A, FRENKEL I. Recent advances in system reliability:Signatures, multi-state system and statistcal inference[M].London: Springer, 2012: 3-29. |
| [7] | LEVITIN G. The universal generating function in reliability analysis and optimization[M].London: Springer, 2005: 61-67. |
| [8] | LISNIANSKI A. Maintenance contract assessment for aging systems[J].Quality & Reliability Engineering International, 2008, 24(5): 519–531. |
| [9] | 阮渊鹏. 基于蒙特卡洛模拟的复杂系统可靠性评估方法研究[D]. 天津: 天津大学, 2013: 10-15. RUAN Y P.Reliability evaluation of complex systems based on Monte Carlo simulation[D].Tianjin:Tianjin University, 2013:10-15(in Chinese). |
| [10] | 肖刚. 评估复杂可维修系统可靠度与瞬态可用度的蒙特卡洛方法[J].兵工学报, 2002, 23(2): 46–50. XIAO G. A Monte Carlo method for obtaining reliability and availability confidence limits of complex maintenance system[J].Acta Armamentarii, 2002, 23(2): 46–50.(in Chinese) |
| [11] | 郭卫华, 徐厚宝, 朱广田. 两部件并联维修系统解的渐近稳定性[J].系统工程理论与实践, 2006, 26(12): 62–68. GUO W H, XU H B, ZHU G T. Asymptotic stability of solution for a parallel maintenance system with two components[J].System Engineering-Theory & Practice, 2006, 26(12): 62–68.DOI:10.3321/j.issn:1000-6788.2006.12.009(in Chinese) |
| [12] | 徐厚宝, 郭卫华, 于景元, 等. 一类串联可修复系统的稳态解[J].应用数学学报, 2006, 29(1): 46–52. XU H B, GUO W H, YU J Y, et al. The asymptotic stability of a series repairable system[J].Acta Mathematic Application Sinica, 2006, 29(1): 46–52.(in Chinese) |
| [13] | 郭卫华. 两相同部件冷贮备可修系统解的定性分析[J].应用泛函分析学报, 2002, 4(4): 376–382. GUO W H. The qualitative analysis of solution of cold redundant repairable with two indentical components[J].Acta Analysis Functionlis Applicata, 2002, 4(4): 376–382.(in Chinese) |
| [14] | 范若楠. 可修系统瞬态指标逼近理论与方法[D]. 北京: 北京理工大学, 2015: 10-18. FAN R N.Approximating theory and method for instantaneous indexes of repairable system[D].Beijing:Beijing Institute of Technology, 2015:10-18(in Chinese). |
| [15] | 王立超, 杨懿, 邹云. 离散时间单部件可修系统瞬时可用度的渐近稳定性[J].数学的实践与认识, 2010, 40(23): 119–123. WANG L C, YANG Y, ZOU Y. The asymptotic stability of the instantaneous availability for the one-unit repairable system[J].Mathematic in Practice and Theory, 2010, 40(23): 119–123.(in Chinese) |
| [16] | 王立超, 杨懿, 邹云, 等. 离散Weibull分布下实现系统可用度的最小波动[J].系统工程学报, 2010, 27(5): 575–581. WANG L C, YANG Y, ZOU Y, et al. Undulation analysis of instantaneous availability under discrete Weibull distributions[J].Journal of System Engineering, 2010, 27(5): 575–581.(in Chinese) |
| [17] | 徐宗昌. 保障性工程[M].北京: 兵器工业出版社, 2002: 50-65. XU Z C. Supportablity engineering[M].Beijing: Weapon Industry Press, 2002: 50-65.(in Chinese) |
| [18] | 文佳, 康锐. 平均维修保障等待时间的计算方法[J].北京航空航天大学学报, 2010, 36(4): 451–454. WEN J, KANG R. Calculation methods for mean waiting time of maintenance support[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(4): 451–454.(in Chinese) |
| [19] | 陈翔. 基于Petri网及矩母函数的计划评审技术[J].北京理工大学学报, 2010, 30(9): 1121–1125. CHEN X. Program evaluation and review technique based on pertinent and moment generating function[J].Transactions of Beijing Institute of Technology, 2010, 30(9): 1121–1125.(in Chinese) |
| [20] | 陈翔. 基于广义随机Petri网的工作流性能分析[J].计算机集成制造系统, 2003, 9(5): 399–402. CHEN X. Performances analysis of workflows based on generalized stochastic Petri nets[J].Computer Integrated Manufacturing Systems, 2003, 9(5): 399–402.(in Chinese) |
| [21] | 葛季栋, 胡昊, 吕建. 一种基于不变量的从工作流网PERT图的转换方法[J].电子学报, 2008, 36(5): 893–898. GE J D, HU H, LV J. A transformation approach from workflow net to PERT diagram based on invariants[J].Chinese Journal of Electronics, 2008, 36(5): 893–898.(in Chinese) |
