自然界中展翅飞翔的各种昆虫大多会采用一种常见的飞行姿态，那就是悬停飞行。无论是被人们广泛探讨的果蝇、蜂蝇、蜜蜂和鹰蛾等昆虫所采用的“正常悬停”^[1]的悬停飞行方式，还是最近被关注的食蚜蝇和蜻蜓所采用的“非正常悬停”^[2]的飞行方式。人们在研究这些昆虫悬停飞行时的气动力、能耗与动稳定性问题时通常假设翅在平均拍动平面内拍动，即假设翅尖轨迹总是位于平均拍动平面内^[3-10]。实际上，昆虫飞行时其翅尖大多不是绝对位于一个平面内，而是不同程度地偏离平均拍动平面，从而形成类似“U”形、“8”字形和椭圆形等各式各样的翅尖轨迹^[11-13]。文献[14]通过研究不同形式的翅尖轨迹对昆虫悬停时气动力的影响，发现大多数昆虫翅尖轨迹的时均气动力与翅尖无偏离的情况相比变化不大(平均升力系数的变化一般不超过6%)。文献[15]则研究了昆虫前飞时“O”字形和“8”字形拍翼轨迹对气动力的影响，结果表明这2种拍翼轨迹都会提高升力。
以上研究工作都是针对正常悬停的昆虫翅尖轨迹对气动力的影响，而非正常悬停时，昆虫也会表现出“U”形的翅尖轨迹^[2]，那么在非正常悬停的情况下翅尖轨迹会对昆虫飞行时的气动力和能耗产生怎样的影响呢？本文基于已有的食蚜蝇悬停飞行时翅膀拍动的运动学数据，以及身体和翅膀的形态学数据^[2]，运用数值模拟的方法分别计算了假设情形下的翅尖轨迹所产生(即忽略食蚜蝇翅膀拍动过程中的抬升角，认为其拍动过程中翅膀始终在同一个平面上，其他参数仍与实验数据相同，本文中用Normal表示这种情形)的气动力与能耗；并将真实翅尖轨迹的情形(本文中用Real表示这种情形)与之进行比较。
1 模型描述与算法 1.1 计算模型及参数 文献[16-17]的研究表明，翅膀的褶皱以及拍动过程中翅膀的变形对气动力的影响不大，因此可忽略翅膀的褶皱和变形，将昆虫的翅膀模型视为刚性平板翼。本文中模型的平面形状取自真实翅膀的扫描图像^[2]，厚度为平均弦长c的3%，前后缘为圆弧。模型翅膀的网格采用文献[18]中介绍的泊松方程求解生成，生成的网格为O-H型网格。翅的网格平面如图 1(a)所示，网格剖面如图 1(b)所示。翅网格的维数为100×99×130，分别为法向、周向和展向的网格点数，翅面法向第1层网格间距为0.001c，网格在法向方向上远场边界距翅膀20倍平均弦长，展向方向上远场边界距翅膀6倍平均弦长。

图 1 翅网格的平面形状和剖面形状 Fig. 1 Plane shape and sectional shape of wing grid

图选项

与实验观测所使用的各角度量相同^[2]，β为拍动平面与水平面的夹角，翅膀转动的3个欧拉角是基于拍动平面坐标系(OXYZ)定义的(Oxyz为有抬升角时固定在昆虫翅膀上随翅膀一起运动的坐标系，Ox′y′z′为忽略抬升角时固定在翅膀上的坐标系)，ψ、θ和?分别为翅膀的翻转角(由翻转角可以确定翅膀的攻角α，下拍过程中，α=ψ；上拍过程中，α=180°-ψ)、抬升角和拍动角，如图 2所示。实验观测结果表明，4只食蚜蝇的拍动频率介于160~190 Hz之间，拍动幅度介于65°~85°之间；上下拍中部攻角的数值差别较大，下拍中部的攻角为50°左右，上拍中部的攻角为20°左右，翅膀的抬升角的数值相对较小(HF1、HF2、HF3和HF4的平均抬升角分别为6°、0°、4°和1°，抬升角的幅度分别为4°、5°、5°和6°)；在上下拍起始和结束时刻要比拍动中部的大，这样就使得翅尖的拍动轨迹呈现出浅“U”形。图 3给出了4只食蚜蝇的翅尖轨迹。由于食蚜蝇悬停时其翅膀是周期性运动的，所以选用傅里叶级数对其实验测得的运动学数据^[2]进行拟合。在对这些数据进行拟合的过程中，需要保证拟合曲线与数据点之间的残差呈随机分布的规律，因此用1阶傅里叶级数来拟合翅膀的拍动角?，用4阶和2阶傅里叶级数分别拟合翅膀的翻转角ψ和抬升角θ。

图 2 拍动平面与翅膀拍动姿态角的定义 Fig. 2 Definition of flapping plane and flapping wing attitude angle

图选项

图 3 4只食蚜蝇的翅尖轨迹 Fig. 3 Wing-tip trajectories of four hoverflies

图选项

4只食蚜蝇形态学参数、雷诺数Re、翅膀的拍动参考速度U及拍动的无量纲周期τ均与文献[2]中采用的数据相同。
1.2 Navier-Stokes方程及计算方法 在惯性坐标系OXYZ下，三维非定常不可压Navier-Stokes方程的无量纲形式为

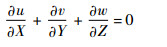(1)

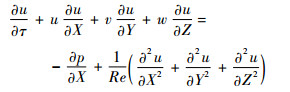(2)

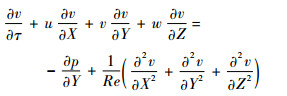(3)

(4)

式中：u、v和w分别为无量纲速度的3个分量；p为无量纲压力；Re为雷诺数，定义为Re=cU/ν，ν为运动黏性系数。
Navier-Stokes方程的数值解法采用文献[19-20]所发展的拟压缩性算法求解。下面简单介绍该算法：在连续方程中加入压力对拟时间的偏导数项，这样物理上相当于把不可压缩流变成可压缩流。动量方程的时间导数项采用2阶的三点后差来离散，黏性项近似采用2阶中心差分离散，对流项采用基于矢通量分裂方法的迎风差分来离散，这里内部网格点采用3阶的迎风差分格式离散，边界点采用2阶迎风差分格式。在求解时间离散的动量方程时，为保证速度散度为零(即满足不可压条件)，每个物理时间步用拟时间步进行内迭代，直到压力对虚拟时间的导数近似为零，此时新时间步的速度散度就近似为零，对在离散点上的代数方程组用线性Gauss-Seidel方法进行迭代求解。关于远场边界条件，在入流边界，速度分量采用自由流条件，而压力用内点插值得到；在出流边界，压力为自由流的静压，而速度用内点插值得到。在翅膀物面，采用无渗透和无滑移条件，物面的压力用相对运动坐标系的动量方程的法向分量方程计算得到。关于计算方法的详细描述参见文献[2-3]。在计算气动力时，原则上需要计算绕昆虫的身体及双翅的流场，但是文献[21-22]的研究表明，在悬停飞行时，除了“打开/合拢”运动，左右翅的相互干扰几乎可以忽略不计。文献[22-24]的计算结果表明，有翅/身干扰时的气动力与无干扰时只相差不到2%，翅膀与身体之间的相互干扰可以忽略。因此，可以认为翅/身干扰与翅/翅干扰都是可以忽略的。这样，在本文的流场计算中，气动力计算都不再考虑身体的影响并忽略双翅间的干扰，只求解单个翅的流场即可。
得到Navier-Stokes方程的数值解后，离散的网格点上每个时刻的速度分量和压力都可以得到。翅膀上的气动力(包括举力V和水平力H)可以通过翅面上的压力和黏性力得到。举力系数C_V、水平力系数C_H、升力系数C_L和阻力系数C_D分别定义为：C_V=V/(0.5 ρU²S)，C_H=H/(0.5 ρU²S)，C_L=L/(0.5 ρU²S)，C_D=D/(0.5 ρU²S)，ρ为流体的密度，S为翅膀的面积。
2 结果与讨论 2.1 翅尖轨迹对气动力的影响 由图 3可以看出，4只食蚜蝇翅尖的拍动轨迹均呈现出浅“U”形, 并且其他运动学数据也类似，此处仅对HF1在2种翅尖轨迹下的计算结果详加讨论。图 4给出了一个拍动周期内的C_V、C_H、C_L和C_D的时间过程曲线。图中：为无量纲时间。由图 4(a)可以看出，在下拍的前半段(=0~0.250)和上拍的前半段(=0.500~0.800)，Real情形下所对应的C_V比Normal情形下的要大。这是很显然的，因为食蚜蝇悬停飞行的举力是由翅膀的升力和阻力共同贡献的^[2]，在每次拍动的前半段，翅尖偏离最高位置向下运动，这个向下的运动速度增大了翅的有效攻角，使得其升力和阻力增加(见图 4(c)和图 4(d)中=0~0.250和=0.550~0.800时段)，或者其升力虽未增加但阻力增量较大(见图 4(c)和图 4(d)中=0.500~0.550时段)。翅的有效攻角的变化可从图 5给出的=0.200和=0.625时刻r₂剖面处的瞬时流线得出。对于Normal情形(见图 5(b)、图 5(d))，所见到的翅来流与翅弦的夹角(有效攻角)较小；而对于真实翅尖轨迹(见图 5(a)、图 5(c))，其有效攻角较大。

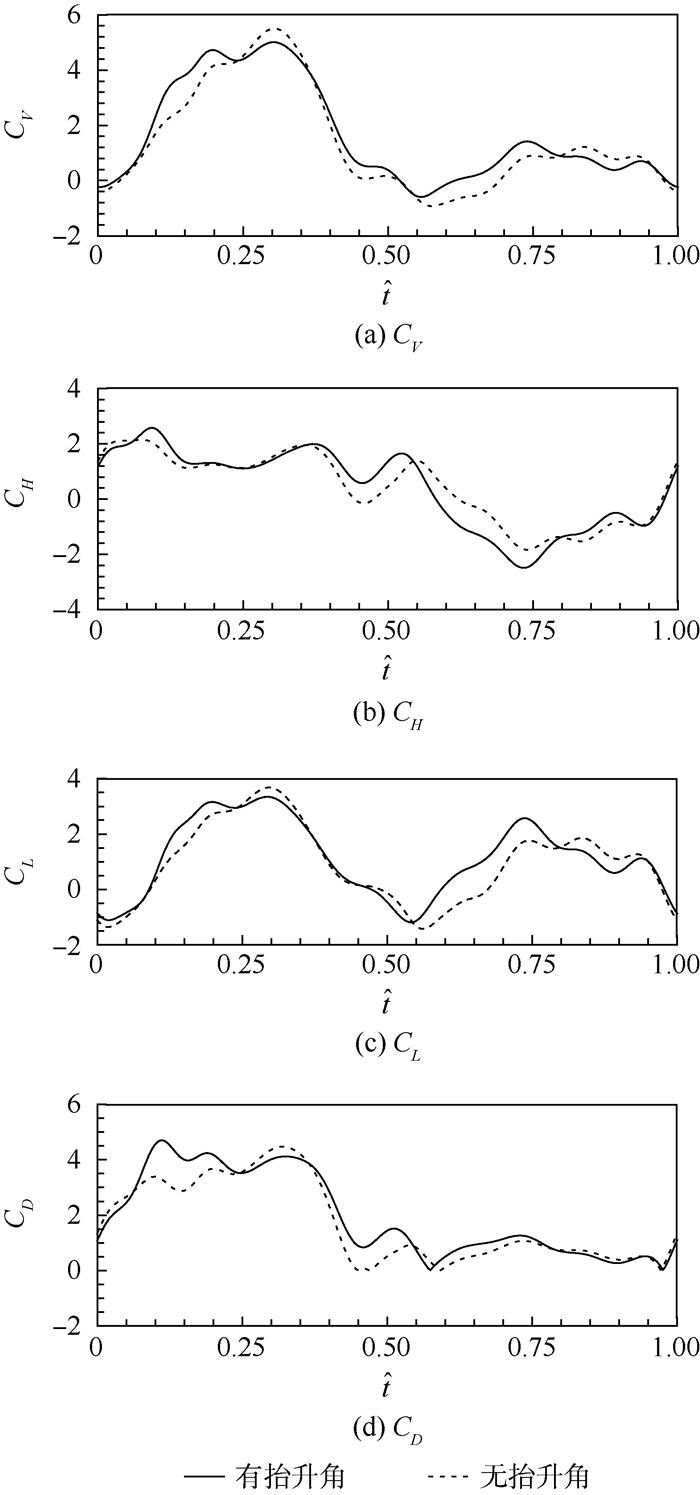图 4 2种翅尖轨迹的CV、CH、CL和CD在一个拍动周期内的变化曲线 Fig. 4 Times courses of computed coefficients CV, CH, CL and CD of HF1 in one cycle

图选项

图 5 2种翅尖轨迹在=0.200和=0.625时刻r2剖面处的瞬时流线 Fig. 5 Streamline plots at spanwise location r2 at =0.200 and =0.625 of two types of wing-tip trajectories

图选项

与此相反，在下拍(=0.250~0.380)或上拍后半段的大部分范围内(=0.800~0.920)，Real情形下的翅尖轨迹所对应的C_V(见图 4(a)中的曲线)比Normal情形下的要小。这也是很显然的，因为在每次拍动的后半段，翅尖向上运动回到最高位置，这个向上的运动速度减小了翅的有效攻角，使得举力减小。这可从图 6给出的=0.350和=0.875时刻r₂剖面处的瞬时流线得出。以上分析表明，当翅尖存在上下运动速度时，气动力会发生较大变化，原因是有效攻角发生了改变。对于=0.380~0.500时段内，Real情形下的举力比Normal情形下的大，这主要是因为此时段内处于下拍结束阶段，翅膀处于快速翻转状态，此时攻角超过65°，已经失速，抬升角速度向上使得Real情形下有效攻角减小，这反而会使其产生的举力比Normal情形下的大，并且此时抬升角较大，附加转动效应也会引起举力的增大。综合上述2种因素，所以此时段内Real情形下的举力比Normal情形下的大。

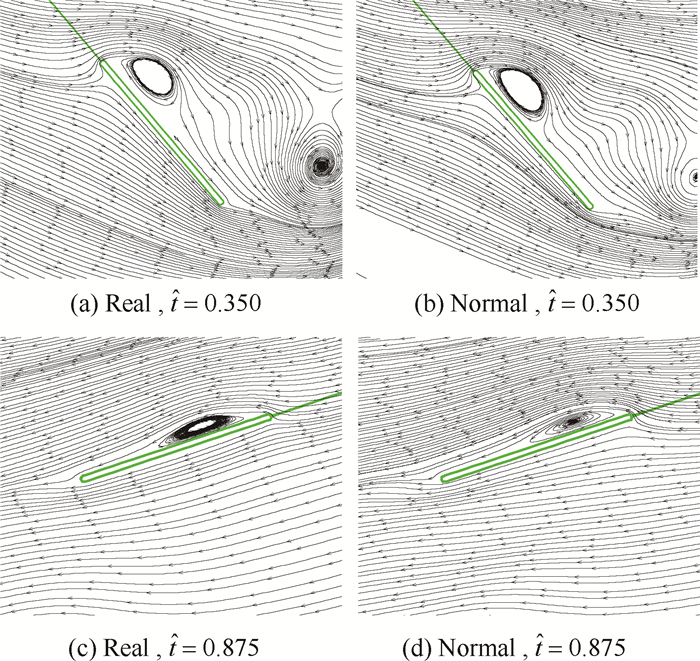图 6 2种翅尖轨迹在=0.350和=0.875时刻r2剖面处的瞬时流线 Fig. 6 Streamline plots at spanwise location r2 at =0.350 and =0.875 of two types of wing-tip trajectories

图选项

下面详细解释附加转动效应，如图 7所示。在=0.380~0.500时段内，翅膀处于下拍结束阶段，此时抬升角变大。这里气动力的改变应该是由于翅尖偏离平均拍动平面的位置引起的，此时翅绕Z轴的转动会引入一个绕翅展向轴的附加转动效应，这个效应会使气动力发生改变。图 8给出了模型翅在拍动过程中某一时刻的位置示意图，其坐标系的定义与图 2一致。假设该时刻翅的展向与平均拍动平面的夹角为θ，翅以角速度ωZ绕Z轴转动。可见，角速度矢量ω_Z可分解成2个正交分量ω_y与ω_z。其中沿翅的展向方向，使得翅有绕y轴转动的效果。这个附加的转动效应会对气动力产生影响：如果θ为正，即翅尖轨迹位于拍动平面上方时，则ω_y指向y轴正方向，使得翅有上仰转动的效果，从而使举力增加；相反若θ为负，则ω_y指向y轴负方向，使得翅有下俯转动的效果，从而使举力减小，这与之前的研究^{[14, 25]}相同。

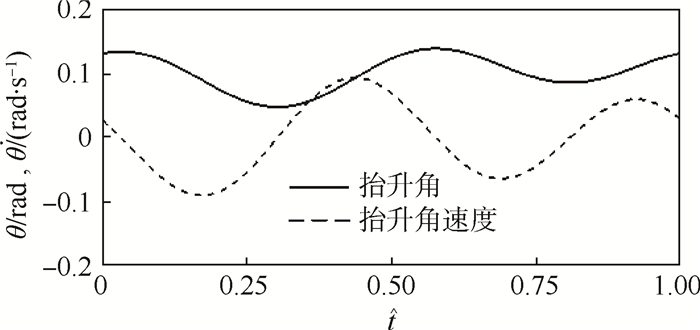图 7 HF1真实翅尖轨迹的抬升角及无量纲抬升角速度曲线 Fig. 7 Curves of deviation angle and non-dimensional deviation angular velocity of HF1 in real wing tip trajectory

图选项

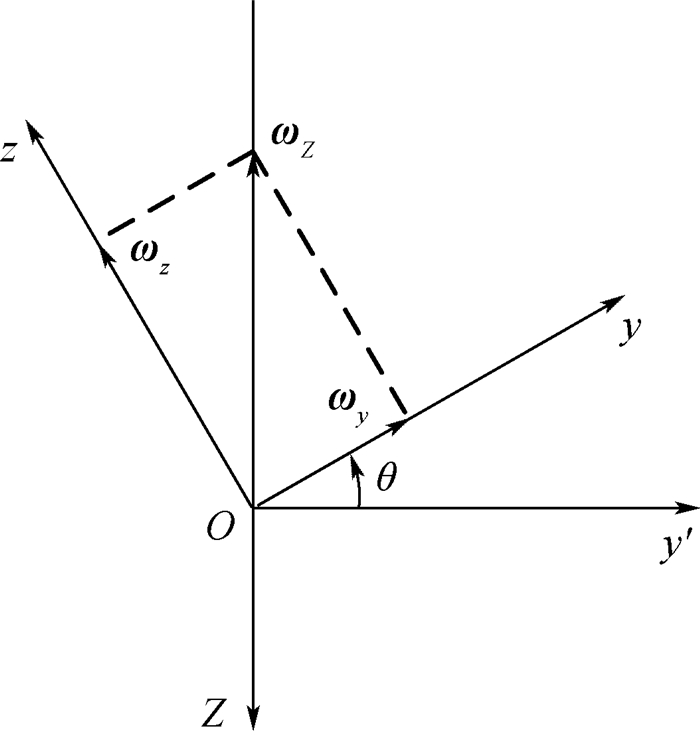图 8 各坐标轴角速度矢量示意图 Fig. 8 Schematic diagram of angular velocity vector in different axes

图选项

从以上分析可以看出，Real情形在上下拍的前半部分产生的举力比Normal情形下大，但上下拍的后半部分要比Normal情形下小。为比较一个周期内2种情形下的气动力差异，分别计算了4只食蚜蝇在上述2种情形下所对应的平均气动力系数，结果如表 1所示。可以看出，对于HF1、HF2和HF3，抬升角的存在使得平均举力系数分别增大了约16.4%、10.8%和11.8%，说明抬升角的存在使得有效攻角变大，对平均举力的增大产生了主导作用。但HF4的平均举力系数基本没有变化，这是因为HF4在下拍过程中和其他3只食蚜蝇相同，由于抬升角的存在使得有效攻角变大，Real情形下的举力比Normal情形下大；而上拍过程中的前半段抬升角均为负值(见图 3)，且此时段内抬升角速度也为负值，这使得其有效攻角反而比Normal情况下小，产生的举力也要小得多，这样使得一个拍动周期的平均举力系数的增量很小。2种情形下的平均水平力系数基本没有变化，这是因为上下拍过程中翅尖偏离平均拍动平面的变化趋势相对平均拍动位置较为对称，一个拍动周期内水平气动力的增加量与减小量可以大致抵消。
2.2 翅尖轨迹对能耗的影响 通过第2.1节的分析发现，抬升角的存在增大了Real情形下的平均举力，那么平均举力改变是否会引起其能耗的增加呢？昆虫翅膀在拍动运动过程中的能耗P为

(5)

式中：M_a为绕翅膀根部的气动力矩；M_i为绕翅膀根部的惯性力的力矩；Ω为翅膀的角速度矢量。
由表 1可以发现，假设Normal情形下产生的平均举力变小，不足以平衡昆虫的体重，因此无法使用总功率P来衡量对比2种情形下的能耗。并且由于假设情形中昆虫翅膀不再偏离平均拍动平面，惯性力矩M_i做功的部分中就缺失了θ和的贡献，所以此处不计惯性力做功消耗的功率，只考虑气动力矩M_a做功的部分所消耗的功率。M_a可由翅膀上气动力的分布计算得到，由气动力矩产生的功率系数C_{P, a}定义为：C_{P, a}=M_a·Ω/(0.5ρU²Sc)，对一个拍动周期内的C_{P, a}进行积分可得气动力矩消耗的功率系数C_{W, a}。由于2种情形下产生的举力不同，消耗的气动功率也不同，因此将单位平均举力所需的气动功系数C_{W, a}/C_V作为考察不同情形能耗的标准。从表 2中可见，4只食蚜蝇Real情形下翅尖轨迹的C_{W, a}/C_V都比Normal的情形小。这表明当翅尖偏离平均拍动平面时，会降低能耗的需要，这是因为在上下拍的前半段(即=0.250和=0.750时刻之前)，翅尖具有较大的偏离平均拍动平面的运动速度，而在相应的时间段内升力和阻力很大，所以此时大的会使气动功率有较大幅度的增加，相应地，举力随之加大。但总的看来，翅尖轨迹对能耗的影响并不大，Real情形下对应的C_{W, a}/C_V较之Normal情形下降低的幅度均为3%左右。
表 1 4只食蚜蝇2种翅尖轨迹的平均举力系数和平均水平力系数 Table 1 Mean vertical and horizontal force coefficients of four hoverflies in two types of wing-tip trajectories

翅尖轨迹情形	HF1			HF2			HF3			HF4
	CV	CH		CV	CH		CV	CH		CV	CH
Normal	1.40	0.40		1.67	-0.09		1.52	0.31		1.70	0.35
Real	1.63	0.38		1.85	-0.11		1.70	0.29		1.71	0.35

表选项






表 2 4只食蚜蝇2种翅尖轨迹气动功率系数与平均举力系数的比值 Table 2 Ratio of aerodynamic power coefficient to mean vertical force coefficient of four hoverflies in two types of wing-tip trajectories

翅尖轨迹情形	CW, a/CV
	HF1	HF2	HF3	HF4
Normal	9.00	8.82	10.14	10.63
Real	8.69	8.45	9.88	10.22

表选项






3 结论 1)食蚜蝇在悬停飞行时，抬升角的存在使得食蚜蝇的翅尖轨迹为“U”形，这种情形下产生的维持体重所需的举力比Normal情形下的举力大10%左右。
2)举力的改变是由两方面原因引起的：一方面是由于抬升角增大了来流与翅膀之间的夹角，即增大了翅膀的有效攻角；另一方面是当翅尖轨迹不在平均拍动平面内时，翅的转动会引入一个绕翅展向轴的附加转动效应，这个效应会使气动力发生变化。
3)抬升角的存在使得食蚜蝇产生相同举力的同时能耗比Normal情形下低3%左右。

参考文献

[1]	WEIS-FOGH T. Quick estimates of flight fitness in hovering animals, including novel mechanism for lift production[J].Journal of Experimental Biology, 1973, 59(1): 169–230.
[2]	MOU X L, LIU Y P, SUN M. Wing motion measurement and aerodynamics of hovering true hoverflies[J].Journal of Experimental Biology, 2011, 214(17): 2832–2844.DOI:10.1242/jeb.054874
[3]	SUN M, TANG J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J].Journal of Experimental Biology, 2002, 205(1): 55–70.
[4]	SUN M, DU G. Lift and power requirements of hovering insect flight[J].Acta Mechanica Sinica, 2003, 19(5): 458–469.DOI:10.1007/BF02484580
[5]	ZHANG Y L, SUN M. Dynamic flight stability of hovering model insects:Theory versus simulation using equations of motion coupled with Navier-Stokes equations[J].Acta Mechanica Sinica, 2010, 26(4): 509–520.DOI:10.1007/s10409-010-0360-5
[6]	DU G, SUN M. Aerodynamic effects of corrugation and deformation in flapping wings of hovering hoverflies[J].Journal of Theoretical Biology, 2012, 300(7): 19–28.
[7]	MOU X L, SUN M. Dynamic flight stability of a model hoverfly in inclined-stroke-plane hovering[J].Journal of Bionic Engineering, 2012, 9(3): 294–303.DOI:10.1016/S1672-6529(11)60123-6
[8]	LIANG B, SUN M. Dynamic flight stability of a hovering model dragonfly[J].Journal of Theoretical Biology, 2014, 348(7): 100–112.
[9]	XU N, SUN M. Lateral dynamic flight stability of a model hoverfly in normal and inclined stroke-plane hovering[J].Bioinspiration & Biomimetics, 2014, 9(3): 036019.
[10]	SUN M. Insect flight dynamics:Stability and control[J].Reviews of Modern Physics, 2014, 86(2): 615–646.DOI:10.1103/RevModPhys.86.615
[11]	ELLINGTON C P. The aerodynamics of hovering insect flight.Ⅲ.Kinematics[J].Philosophical Transactions of the Royal Society B, 1984, 305(1122): 41–78.DOI:10.1098/rstb.1984.0051
[12]	FRY S N, SAYAMAN R, DICKINSON M H. The aerodynamics of free-flight maneuvers in drosophila[J].Science, 2003, 300(5618): 495–498.DOI:10.1126/science.1081944
[13]	LIU Y, SUN M. Wing kinematics measurement and aerodynamics of hovering droneflies[J].Journal of Experimental Biology, 2008, 211(13): 2014–2025.DOI:10.1242/jeb.016931
[14]	罗国宇.翅膀皱褶和平面形状及翅尖轨迹对昆虫飞行气动力的影响[D].北京:北京航空航天大学, 2005:109-112.LUO G Y.Effect of corrugated wing, planform and wing-tip trajectory on aerodynamics of flight insect[D].Beijing:Beihang University, 2005:109-112(in Chinese).
[15]	余永亮, 童秉纲.拍翼轨迹对昆虫前飞气动性能的影响[C]//第十届全国分离流、旋涡和流动控制会议, 2004:155-159.YU Y L, TONG B G.Effect of flapping wing trajectory on insect forward flight aerodynamic[C]//10th National Separation Flow, Vortex and Flow Control Conference, 2004:155-159(in Chinese).
[16]	DU G, SUN M. Effects of wing deformation on aerodynamic forces in hovering hoverflies[J].Journal of Experimental Biology, 2010, 213(13): 2273–2283.DOI:10.1242/jeb.040295
[17]	MENG X G, XU L, SUN M. Aerodynamic effects of corrugation in flapping insect wings in hovering flight[J].Journal of Experimental Biology, 2011, 214(3): 432–444.DOI:10.1242/jeb.046375
[18]	HILGENSTOCK A.A fast method for the elliptic generation of three dimensional grids with full boundary control[C]//Numerical Grid Generation in Computational Fluid Mechanics' 88.Swansea:Pineridge Press, 1988:137-146.
[19]	ROGERS S E, KWAK D. Upwind differencing scheme for the time-accurate incompressible Navier-Stokes equations[J].AIAA Journal, 1990, 28(2): 253–262.DOI:10.2514/3.10382
[20]	ROGERS S E, KWAK D, KIRIS C. Numerical solution of the incompressible Navier-Stokes equations for steady-state and time-dependent problems[J].AIAA Journal, 1991, 29(1): 603–610.
[21]	SUN M, YU X. Aerodynamic force generation in hovering flight in a tiny insect[J].AIAA Journal, 2006, 44(7): 1532–1540.DOI:10.2514/1.17356
[22]	YU X, SUN M. A computational study of the wing-wing and wing-body interactions of a model insect[J].Acta Mechanica Sinica, 2009, 25(4): 421–431.DOI:10.1007/s10409-009-0266-2
[23]	AONO H, LIANG F, LIU H. Near-and far-field aerodynamics in insect hovering flight:An integrated computational study[J].Journal of Experimental Biology, 2008, 211(2): 239–257.DOI:10.1242/jeb.008649
[24]	LIANG B, SUN M. Aerodynamic interactions between contralateral wings and between wings and body of a model insect at hovering and small speed motions[J].Chinese Journal of Aeronautics, 2011, 24(4): 396–409.DOI:10.1016/S1000-9361(11)60047-2
[25]	LAN S, SUN M. Aerodynamic properties of a wing performing unsteady rotational motions at low Reynolds number[J].Acta Mechanica, 2001, 149(1-4): 135–147.DOI:10.1007/BF01261668