传统的高速穿孔加工采用长电极后推式进给,细长电极的低刚度会产生加工中弯曲变形问题,从而对孔批量化加工精度和效率造成不利影响。针对此问题,清华大学已研发出一种采用夹头夹在电极前端的双夹子蠕动式进给、高精度旋转及高压内冲液的复合功能主轴[2]。但前期实验表明:在加工较大深径比的小孔时,孔深和冲液压力等因素变化对孔径精度和加工效率有明显影响。分析其原因认为:由于电极具有一定的悬伸长度,在较高压力中空冲液扰动的作用下,加工中电极易产生不规则振动现象。这不仅直接影响孔加工尺寸形状精度,而且造成的侧壁放电或短路将使电极频繁回退,也降低孔的加工效率。
目前,高速穿孔加工研究还主要集中在工艺参数优化选择、电极和工件材料特性影响、电极损耗规律等方面[3-5],缺乏对高压中空冲液引起的电极扰动规律研究,国内外研究仅对这种扰动现象进行了一些报道。比如,2013年郭维城等试验研究发现随着孔深增加,电极振动现象加剧[6]。然而,为优化高速穿孔工艺过程,特别是对于加工精度和效率有较高要求的较大深径比小孔批量化加工(比如,航空发动机涡轮叶片气膜冷却孔加工),研究电极扰动规律及其影响因素具有较重要意义和实用价值。
本研究通过建立中空管状电极内冲液物理模型及流固耦合数值仿真模型,并借助ANSYS有限元仿真分析软件平台,综合考虑中空冲液压力、穿孔深度、电极悬长、主轴转速、放电间隙及导向间隙等多参数影响,研究高速穿孔过程中电极振动幅值的影响规律,并通过实验验证仿真结果及规律的正确性。
1 穿孔加工中空管状电极物理及仿真建模 如图 1所示,物理及数值仿真建模过程是基于最新开发的双夹子蠕动式进给主轴。该主轴可实现电极旋转、高压内冲液及蠕动进给功能,通过协调控制常开夹子、常闭夹子及S轴进给运动,实现电极蠕动进给补偿电极损耗,并采用精密导向器约束加工中电极的旋转径跳误差,导向器设计为具有上下导向环的结构来保证导向长度并减少摩擦面积[2]。
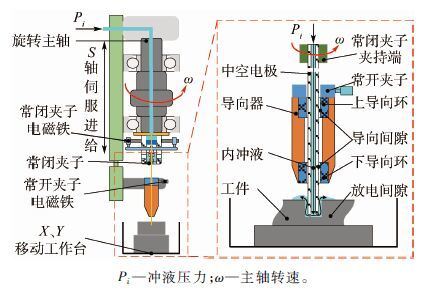 |
| 图 1 高速电火花穿孔加工主轴结构 Fig. 1 Spindle structure used in hole machining by high-speed EDM |
| 图选项 |
根据工作液的流动状态,流场模型求解器设置为耦合、三维、定常流及绝对压力求解算法。放电间隙中工作液流动速度较快,通过雷诺数计算得出工作液流动状态属于湍流。因此数值仿真采用标准的k-ε模型[7-9],湍动能k和耗散率ε的方程为
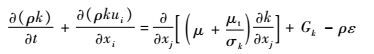 | (1) |
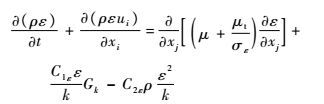 | (2) |
式中:ρ=1.0 g/cm3为工作液密度;σk=1.0、σε=1.3为湍流动能和耗散率的普朗特常数;C1ε=1.44、C2ε=1.92为经验常数;μt为湍流黏度;ui为时均速度;Gk为由于平均速度梯度引起的湍动能量;t为时间;xi和xj为坐标张量;μ为流体动力黏度。
鉴于单向流固耦合中的弱耦合方式易于收敛并满足物理模型(图 1)仿真要求,因此采用单向流固耦合求解方式,依次进行流场计算和结构力学计算。
根据图 1主轴结构参数及k和ε的方程,建立电极振动特性分析的数值仿真物理模型如图 2所示。模型中包含了导向间隙g、穿孔深度h、Pi、ω、放电间隙u和电极悬长L等重要参数。设置边界条件为:定义大气压力作用在放电间隙出口;流场计算中运动边界为流体壁面;结构力学计算中运动边界为旋转电极。为实现流固耦合面数据完全传递,设置流体壁面与中空电极旋转速度大小、方向相同。模型相关参数为:中空冲液为纯净水、电极材料为黄铜、电极中空内径为Φ 0.24 mm、电极外径为Φ 0.5 mm。
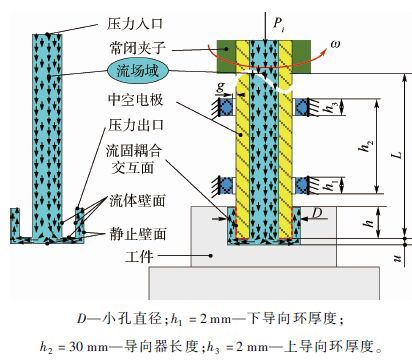 |
| D—小孔直径;h1=2 mm—下导向环厚度; h2=30 mm—导向器长度;h3=2 mm—上导向环厚度。 图 2 数值仿真物理模型及边界条件 Fig. 2 Numerical simulation of physical model andboundary conditions |
| 图选项 |
2 中空冲液电极振动特性数值仿真分析 数值仿真借助Pro/E和ANSYS Workbench软件平台中Fluid Structure Interaction(FSI)单向流固耦合模块,开展中空冲液电极振动幅值特性的仿真分析研究。划分网格时使流场计算与结构力学计算网格交互面节点100%重合,避免因节点不重合造成的数据传递误差[10]。基于考虑工作液高速高压流动、并且及时的冷却作用,忽略非接触式火花放电瞬间较小作用力、瞬时放电温度对电极的影响。
仿真流程如图 3所示,首先通过Pro/E建立几何模型并导入FSI模块中,将结构力学计算模型和流体模型网格化且保证网格节点重合。然后在Fluent中设定模型求解器、能量方程、湍流模型、流体几何属性、边界条件及耦合参数,在Mechanical中设定边界条件和映射激励。最后设置残差系数并初始化求解环境,进行流固耦合求解得到流场压力和中空电极最大变形量。
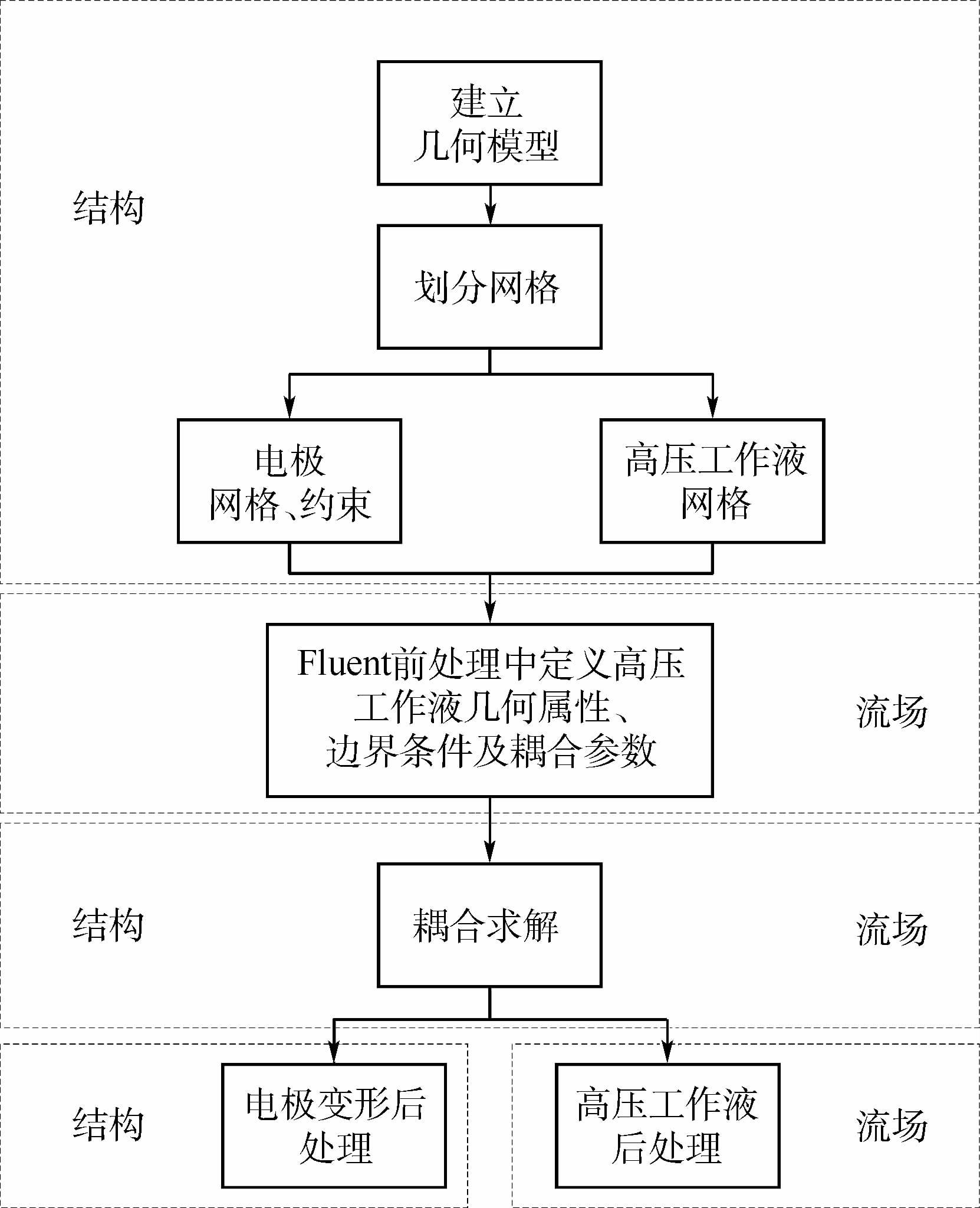 |
| 图 3 仿真分析流程图 Fig. 3 Flowchart of simulation analysis |
| 图选项 |
数值仿真预期得到各个关键单因素、以及多因素耦合对电极振动特性的影响规律,因此首先仿真关键单因素影响,然后正交仿真研究多因素耦合影响规律。采用极差分析、方差分析的统计方法,表征各因素优化规律的可信度。
2.1 关键因素对电极振动特性影响规律 在给定条件下研究Pi、g、h、ω和u等关键因素对电极振动特性的影响规律,利用电极最大变形量表征其影响程度。关键因素仿真参数如表 1所示,对电极振动幅值A的影响规律曲线如图 4所示。
表 1 关键因素仿真参数 Table 1 Simulation parameters of key factors
| 关键因素 | 仿真参数 |
| Pi/MPa | 1,3,5,7,9 |
| g/μm | 1,5,10 |
| h/mm | 1,2,3,6 |
| ω/(r·min-1) | 0,400,800,1 600,3 200 |
| u/μm | 20,40 |
表选项
 |
| 图 4 关键因素与电极振动幅值关系曲线 Fig. 4 Relation curves of key factors andelectrode vibration amplitude |
| 图选项 |
2.1.1 冲液压力对电极振动幅值的影响 电极振动幅值随Pi的变化规律如图 4(a)所示,电极振动幅值随冲液压力Pi的增加逐渐增大,且大于导向器间隙;当Pi=1 MPa时,电极振动幅值即达到10.5 μm(导向间隙10 μm时),但Pi增加到9 MPa时,其振动幅值为11.42 μm,即电极振动幅值波动量小于1.0 μm。这表明若要实现较好的排屑效果(Pi>1 MPa),必然会产生一定的振动幅值(>10 μm),而Pi变化(继续增大时)对电极振动的影响较小。分析认为,放电间隙中工作液流经电极前端面时受小孔底面阻挡,工作液速度的重新分布加剧了工作液主流中的内部摩擦(主流湍动性增加),进而加大了对电极扰动作用,但导向器的约束作用使振幅在较小范围内变化。
2.1.2 穿孔深度对电极振动幅值的影响 如图 4(b)所示,电极振动幅值随h增加而增加,且增长速率随Pi增加而加快;,当Pi保持1 MPa不变时,h从1 mm增加到6 mm时,振动幅值从10.5 mm增大到11.5 μm。但当Pi达到9 MPa时,穿孔深度6 mm时振动幅值甚至达到14 μm,即由此产生的孔径误差可达28 μm。在较深孔加工中为实现有效排屑,孔越深冲液压力要求越高,这时随着孔深增加而产生的电极振动将对孔径误差影响较大。分析认为,这是由于电极悬伸长度增加降低了电极挠曲强度,使电极抵抗弯曲变形能力下降造成的。
2.1.3 主轴转速对电极振动幅值的影响 图 4(c)结果显示,ω在0~3 200 r/min范围内变化时,即使Pi=9 MPa时电极振动幅值变化量仍小于0.3 μm,即主轴转速变化对电极振动的影响甚至可忽略。分析认为,由于电极壁面较光滑,转动时对工作液湍动性影响微弱。
2.1.4 放电间隙对电极振动幅值的影响 图 4(d)结果显示,随着Pi增加,不同放电间隙(u=20,40 μm)曲线交替上升,即表明10 μm量级的加工间隙变化对电极振动幅值影响无明显规律。可以认为在较高中空冲液压力条件下,10 μm量级放电间隙对工作液流动状态影响较小,进而对电极振动幅值影响微弱。
2.1.5 导向间隙对电极振动幅值的影响 根据图 4(e)结果,导向间隙对电极振动幅值产生显著影响。分析h=3 mm的情况:g=1 μm时振动幅值2.4 μm,而g=10 μm时振动幅值达到12.5 μm,即由此产生的孔径误差可达25 μm。这是由于工作液湍流扰动使电极产生了较大的变形,导向器约束振动幅值限制在一定的范围内。为证实分析的正确性,进一步对电极与导向器之间的接触压力进行分析如图 5所示,当Pi=4 MPa,g=20 μm,h=1 mm时存在接触压力0.046 MPa,即导向器对电极具有约束作用。因此,实际加工中应尽可能减小导向器间隙,以降低电极振动幅值,提高孔径尺寸精度。
 |
| 图 5 电极与导向器接触压力分布 Fig. 5 Contact pressure distribution of electrodeand guide apparatus |
| 图选项 |
2.2 多因素耦合对电极振动特性影响规律 进而通过正交仿真研究多因素耦合作用效果,为指导加工工艺提供依据。根据实际加工经验选取加工参数范围,如表 2所示采用5因素5水平进行正交数值仿真研究,导向间隙根据实际情况取值为10 μm。
表 2 多因素耦合水平正交表 Table 2 Level orthogonal array of multi-factor coupling
| 水平 | 仿真因素 | ||||
| Pi/MPa | h/mm | L/mm | ω/(r·min-1) | u/μm | |
| 1 | 1 | 1 | 83 | 200 | 20 |
| 2 | 2 | 2 | 84 | 400 | 30 |
| 3 | 3 | 3 | 85 | 600 | 40 |
| 4 | 4 | 4 | 86 | 800 | 50 |
| 5 | 5 | 5 | 87 | 1 000 | 60 |
表选项
通过数据统计分析方法评价多因素影响权重,均值与极差分析结果如图 6所示。得到优化水平依次为Pi(1)、h(1)、L(5)、ω(4)、u(3),即得到一组优化组合为:Pi=1 MPa,h =1 mm,L =87 mm、ω=800 r/min、u =40 μm。极差分析中,较大数值说明该因素对电极振动幅值影响能力较大,由极差分析可得对电极振动幅值影响的主次顺序为:穿孔深度、冲液压力、放电间隙、主轴转速、电极悬长。
 |
| 图 6 正交仿真均值与极差分析 Fig. 6 Mean and range analysis of orthogonal simulation |
| 图选项 |
为验证数值仿真结果的可信度,对其进行方差分析,引入误差列e进行结果有效性评估[11-12]。方差分析结果如图 7所示,因素的偏差平方和均大于e的偏差平方和,可认为数值仿真结果有效。为得到因素的显著性水平,查询F分布表知F0.05=6.390,由Fh=11.730(Fh为h的F统计量)且满足Fh> F0.05,则有95%的把握认为穿孔深度h对电极振动有显著的影响。同理,由FPi=5.134(FPi为Pi的F统计量)且满足 F0.05>FPi>F0.1,则有90%的把握认为冲液压力Pi对电极振动影响显著。同时L、ω、u的F统计量均小于F0.1,说明这些因素对电极振动的影响不显著。通过方差分析F统计量大小得到因素主次排列顺序为:穿孔深度、冲液压力、放电间隙、主轴转速、电极悬长。与极差分析结果一致,表明了数值仿真结果的准确性。
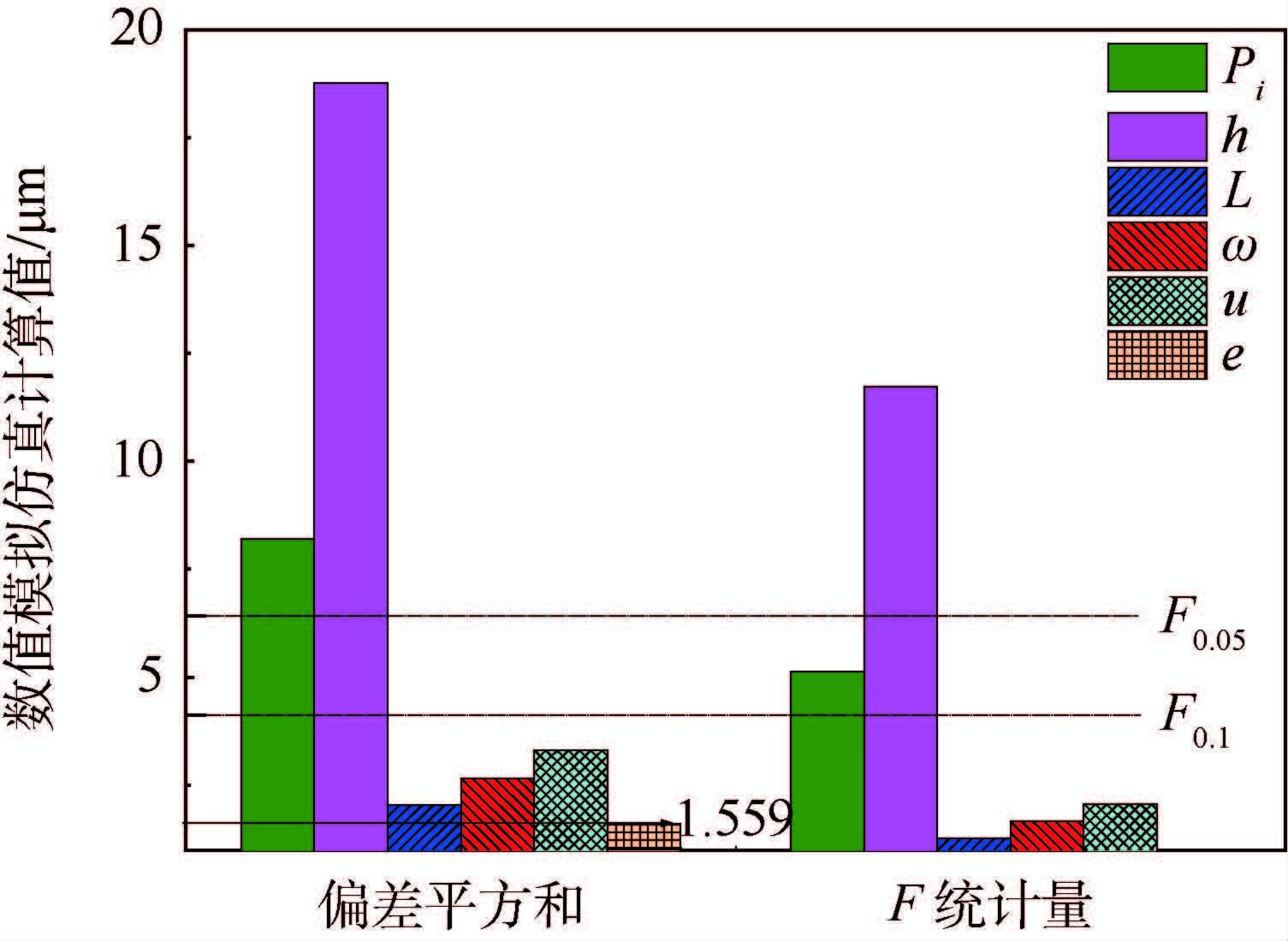 |
| 图 7 正交仿真方差分析 Fig. 7 Variance analysis of orthogonal simulation |
| 图选项 |
3 电火花穿孔加工过程实验验证 受到实验系统限制,实验验证无法达到仿真研究所覆盖的参数范围。但为验证仿真结果的正确性,根据实验机床能达到的系统参数,开展内冲液压力、穿孔深度和主轴转速的趋势性验证实验。基本实验条件如表 3所示,不同因素的参数变化范围如表 4所示。采用中空电极(内径240 μm、外径500 μm、长度400 mm)、高压内冲液方式,每个验证实验参数下分别加工出3个通孔。根据通孔直径与电极振动幅值具有正相关性,通过测量多个小孔直径取平均值的方法,实验得到各因素与电极振动幅值的关系。
表 3 电火花穿孔加工实验基本参数 Table 3 Basic parameters of EDM drillingprocessing experiment
| 参数 | 数值 |
| 电压/ V | 90 |
| 峰值电流/ A | 10 |
| 脉宽/ μs | 24 |
| 脉间/μs | 40 |
| 注:工件材料为Inconel 738;电极材料为黄铜;电极类型为中空管状;工作液为纯净水。 | |
表选项
表 4 实验验证参数变化范围 Table 4 Parameters range of verification experiments
| 参数 | 范围 |
| Pi/ MPa | 1,1.5,2,2.5,3,3.5,4 |
| h/ mm | 2,3,4,6 |
| ω/ (r·min-1) | 100,120,140,160,180 |
表选项
在h=6 mm、ω=140 r/min参数条件下,依次进行不同内冲液压力下对比加工实验。加工出的孔出、入口及典型通孔脱模显微镜测量结果如图 8所示,入口直径为Φ553~571 μm,对应出口直径为Φ552~568 μm。
 |
| 图 8 h=6 mm时阵列孔出、入口及典型通孔脱模尺寸图 Fig. 8 Inlets,outlets and injection models of array holes at h=6 mm |
| 图选项 |
图 8(a)为其他加工参数相同、内冲液压力分别为Pi =4 MPa与Pi =1 MPa所对应的孔入口图,图 8(b)为与之对应的出口图。通过图 8的孔脱模测量可知:与1 MPa冲液压力下加工孔径相比,4 MPa情况下通孔直径较大且最大相差19.7 μm。通过此测量方法,得到孔径平均值随Pi变化曲线如图 9所示,此变化趋势与仿真结果一致,即随着内冲液压力增加而电极振动幅值增大(孔径变大),但孔径变化数值大于仿真振动幅值。从穿孔加工过程来看这样结果也是合理的,因为孔径误差不仅来源于电极振动幅值几何因素,而且振动还会造成更多的二次放电,进一步扩大了加工的孔径。此研究表明在保证有效排屑前提下,适当地减小内冲液的压力有利于提高孔径尺寸精度。
 |
| 图 9 冲液压力与孔径平均值曲线 Fig. 9 Curve of hydraulic pressure of dielectric fluid andmean of aperture |
| 图选项 |
在Pi =4 MPa、ω=140 r/min参数条件下,依次进行不同穿孔深度的对比加工实验。穿孔深度为2 mm的阵列孔及典型通孔脱模测量图如图 10所示。对比图 8(c)与图 10(b)可得,通孔平均值由穿孔深度2 mm的Φ557 μm增加至穿孔深度为6 mm的Φ569 μm,孔径平均值最大相差12 μm。孔径平均值随穿孔深度变化曲线如图 11所示,此实验结果与仿真结果趋势一致,即随着加工深度增加而电极振动幅值增大(孔径变大),但孔径变化数值仍大于仿真振动幅值。
 |
| 图 10 h=2 mm时阵列孔出、入口及典型通孔脱模尺寸图 Fig. 10 Inlets,outlets and injection models of array holes at h=2 mm |
| 图选项 |
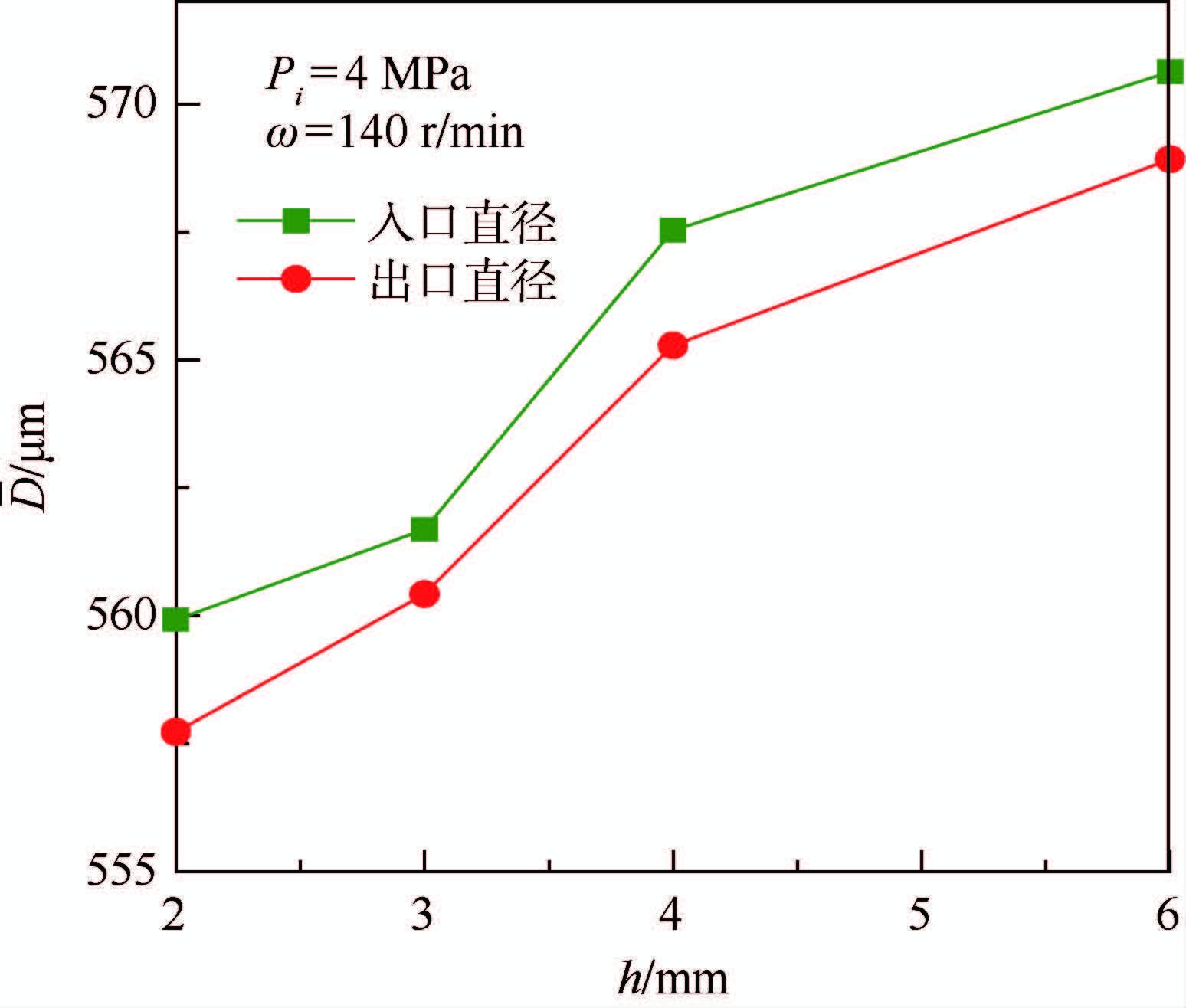 |
| 图 11 穿孔深度与孔径平均值曲线 Fig. 11 Curve of drilling depth and mean of aperture |
| 图选项 |
在Pi =4 MPa、h=6 mm参数条件下,依次进行不同主轴转速参数下对比实验结果如图 12所示,孔径随主轴转速增加呈无规律的震荡状态,且孔径平均值最大差值小于4 μm。这样结果与仿真趋势一致得出:在采用中空冲液的高速电火花穿孔加工中,无需采用过高的主轴转速,这可降低主轴的设计难度,有利于加工系统的稳定运行。
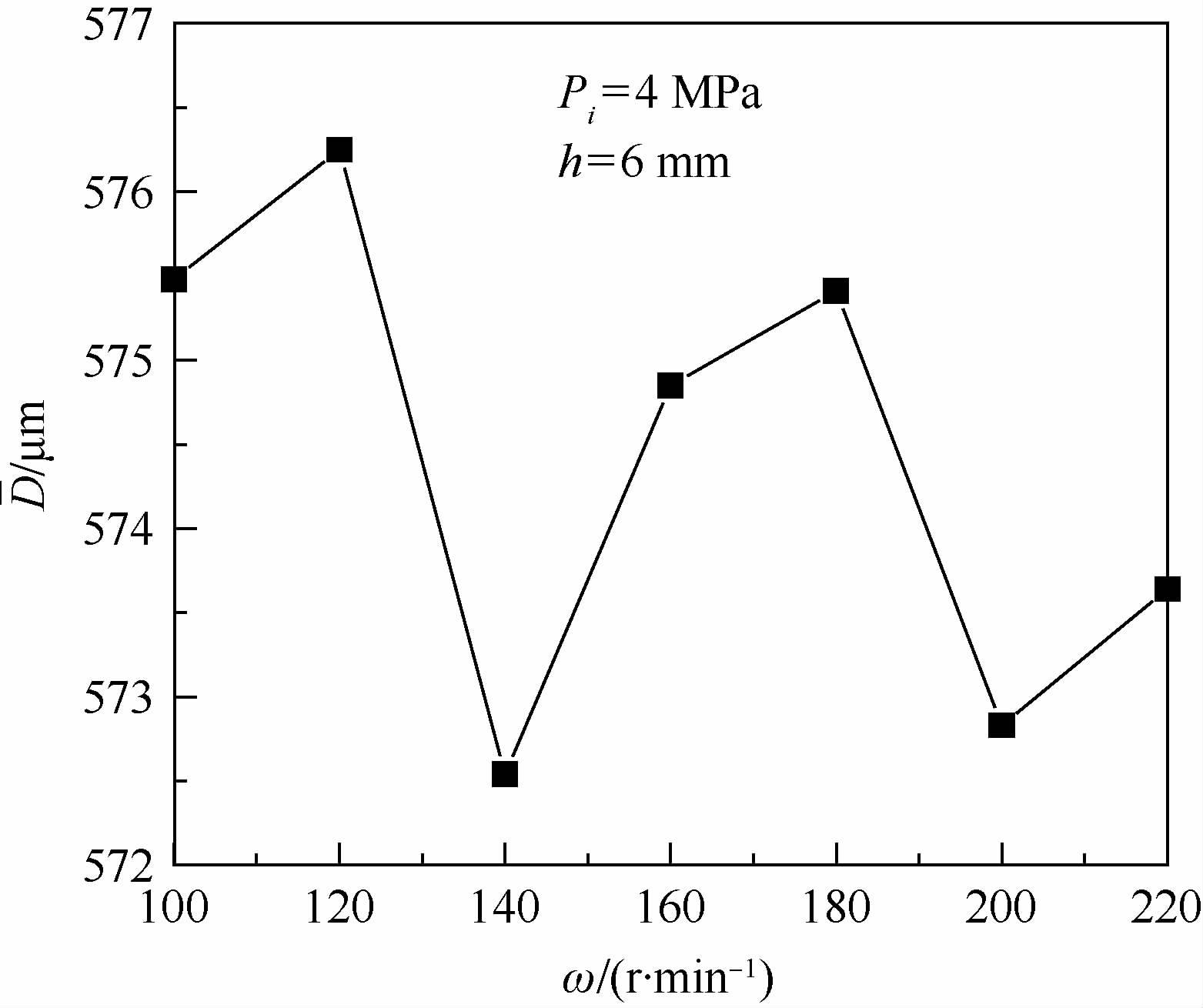 |
| 图 12 主轴转速与孔径平均值曲线 Fig. 12 Curve of spindle speed and mean of aperture |
| 图选项 |
4 结 论 通过流固耦合建模及数值仿真表明,降低冲液压力、减小穿孔深度、减小导向器间隙有利于降低电极振动幅值,提高孔径尺寸复制精度。且在导向器间隙一定的实际情况下,多因素耦合数值仿真分析得到影响电极振动幅值因素显著性排序为:穿孔深度、冲液压力、放电间隙、主轴转速、电极悬长。这从有效控制电极扰动振动的角度,得到改善加工过程和提高孔径复制精度的依据。得出如下主要结论:
1) 通过对比中空冲液电极振动仿真分析和多孔加工实验结果可得,穿孔过程加工实验结果与电极振动数值仿真结果趋势相吻合,但由于孔径误差不仅来源于电极振动幅值几何因素,实验结果中孔径变化数值大于数值仿真振动幅值。
2) 在采用中空冲液的高速电火花穿孔加工中,导向器间隙对电极振动幅值影响最为显著,通过提高导向器导向精度,可有效降低电极振动幅值。且由于主轴转速与电极悬长对电极振动幅值较小的影响作用,因此无需采用过高的主轴转速,这可降低主轴的设计难度,有利于加工系统的稳定运行。
3) 采用脱模观测孔径尺寸方法,实验得到冲液压力从4 MPa降至1 MPa时孔径尺寸可减小19.7 μm,即穿孔深度一定时,在保证有效排屑的前提下,适当减小内冲液压力有利于提高孔径尺寸精度。
参考文献
| [1] | 叶树林, 刘晋春. 高速电火花小孔加工机理的研究[J].电加工, 1997(4): 15–18.YE S L, LIU J C. The research on machining mechanism of high speed small hole EDM drilling[J].Electromachining & Mould, 1997(4): 15–18.(in Chinese) |
| [2] | 王志强, 佟浩, 李勇, 等. 气膜冷却孔电火花加工用复合功能主轴[J].清华大学学报(自然科学版), 2014, 54(9): 1131–1137.WANG Z Q, TONG H, LI Y, et al. Multifunctional spindle for machining film cooling holes in EDM[J].Journal of Tsinghua University (Science and Technology), 2014, 54(9): 1131–1137.(in Chinese) |
| [3] | 刘正勋, 陈祥康. 深小孔的高速电火花加工工艺[J].机械科学与技术, 1989(5): 5–8.LIU Z X, CHEN X K. The machining technology of EDM on deep hole[J].Mechanical Science and Technology, 1989(5): 5–8.(in Chinese) |
| [4] | YILMAZ O, OKKA M A. Effect of single and multi-channel electrodes application on EDM fast hole drilling performance[J].The International Journal of Advanced Manufacturing Technology, 2010, 51(1-4): 185–194.DOI:10.1007/s00170-010-2625-3 |
| [5] | PHAM D T, IVANOV A, BIGOT S, et al. An investigation of tube and rod electrode wear in micro EDM drilling[J].The International Journal of Advanced Manufacturing Technology, 2007, 33(1-2): 103–109.DOI:10.1007/s00170-006-0639-7 |
| [6] | 郭维城, 郭永丰, 侯朋举, 等. 电火花加工阵列穿丝孔的试验研究[J].机械设计与制造, 2013(2): 226–228.GUO W C, GUO Y F, HOU P J, et al. Study on the array wire threading hole test in electrical-discharge process[J].Machinery Design and Manufacture, 2013(2): 226–228.(in Chinese) |
| [7] | 贾振元, 郑新毅, 王福吉, 等. 微孔电火花加工极间工作液流动状态研究[J].大连理工大学学报, 2010, 50(2): 188–193.JIA Z Y, ZHEN X Y, WANG F J, et al. Research on flow state of interelectrode working fluid in micro-EDN[J].Journal of Dalian University of Technology, 2010, 50(2): 188–193.(in Chinese) |
| [8] | 张淑奎, 王燕青, 黄河, 等. 旋转电极内冲液电火花铣削加工流场仿真及实验研究[J].电加工与模具, 2011(1): 1–5.ZHANG S K, WANG Y Q, HUANG H, et al. Research on rotation electrode and iner jetted dielectric EDM milling flow simulation and experiment[J].Electromachining & Mould, 2011(1): 1–5.(in Chinese) |
| [9] | 唐家鹏. Fluent14.0超级学习手册[M].北京: 北京人民邮电出版社, 2013: 30-38.TANG J P. The study guide of Fluent14[M].Beijing: Posts & Telecom Press, 2013: 30-38.(in Chinese) |
| [10] | 黄志新. ANSYS Workbench 14.0超级学习手册[M].北京: 人民邮电出版社, 2013: 505-520.HUANG Z X. The study guide of ANSYS Workbench 14.0[M].Beijing: Posts & Telecom Press, 2013: 505-520.(in Chinese) |
| [11] | 茆诗松. 实验设计[M].2版北京: 中国统计出版社, 2012: 111-123.MAO S S. Design of experiments[M].2nd edBeijing: China Statistics Press, 2012: 111-123.(in Chinese) |
| [12] | 何为. 优化实验设计方法及数据分析[M].北京: 化学工业出版社, 2012: 29-57.HE W. Optimization design of experiment method and data analysis[M].Beijing: Chemical Industry Press, 2012: 29-57.(in Chinese) |
