2008年,欧盟的FP7项目对变形后缘等高升力装置及其驱动机构进行研究[7],以获得预期的外形。美国国防高级研究计划局(Defense Advanced Research Projects Agency,DARPA)启动的“Adaptive Wing(ADIF)”项目应用偏心梁驱动机构[8],对后缘变形进行测试以达到外部加载情况的变形要求。东京大学[9]研究了后缘采用瓦楞结构的变形机翼,可以实现光滑无缝变形,有较好的变形能力。哈尔滨工业大学[10]设计出的可实现后缘变形的索网传动机构,具有放大驱动力,提高变体后缘驱动效率的优点。文献[11]研究了翼型变形驱动装置,以耗费最低能量驱动中弧线变形,进而改善翼型升力。
近年来,波音和NASA正联合设计连续变弯度的后缘襟翼(Variable Camber Continuous Trailing Edge Flap,VCCTEF)系统,主要目标是通过连续改变后缘弯度,提高整个巡航阶段的升阻特性[12, 13]。NASA对VCCTEF的减阻特性作了初步评估:VCCTEF使巡航阻力降低近10%[14]。文献[15]对柔性后缘翼型作了流固耦合分析,研究了后缘刚度对气动力的影响。文献[16]建立了集多模块于一体的优化系统,以减阻为目的对柔性后缘进行了气动外形的优化设计。
杨智春和解江[17]对柔性后缘进行了不同偏转轨迹的方案设计和气动特性分析,研究指出可根据实际需要设计出满足任意后缘偏转要求的自适应机翼。此外,该团队还对柔性后缘机翼进行了操纵特性的研究[18],结果表明,柔性后缘机翼相对于传统刚性机翼,其产生的较大低头力矩会降低操纵效率。陈钱等[19]以变弯度翼型为研究对象,计算了不同偏转外形下的气动力,研究了不同变形参数对气动特性的影响。
国内外****对柔性后缘可变形机翼气动方面的研究,主要集中在对不同轨迹变弯度机翼的气动特性分析及其优化设计方面[14, 16, 17, 18, 19],均未与带缝隙简单襟翼的偏转进行对比研究。另一方面,飞机起飞着陆后缘大角度下偏时,在较大攻角下易引发失速,可变形机翼后缘大偏角下的失速特性有待研究。因此,本文对可变形机翼和常规带简单襟翼机翼(简称常规机翼)的气动特性进行对比研究,然后研究可变形机翼后缘大偏角下的失速特性,并从表面压力分布、流场结构和机翼变形方式等方面研究上述特性产生的机理。
1 可变形机翼柔性后缘模型NASA对VCCTEF作了初步优化,在改善巡航升阻比和压力分布方面,后缘中弧线作类抛物线轨迹变弯的布局是最优的[20]。以NACA0012翼型为基本翼型,其后缘中弧线作抛物线轨迹变弯。柔性后缘为40%机翼弦长,上下偏转范围为±20°。定义转轴点同后缘点的连线与基本翼型弦线的夹角为后缘偏角β,下偏为正。 常规机翼的襟翼与可变形机翼柔性后缘比例相同,参照文献[21]的模型,中间的缝隙取为0.3%机翼弦长,2种机翼如图 1所示。
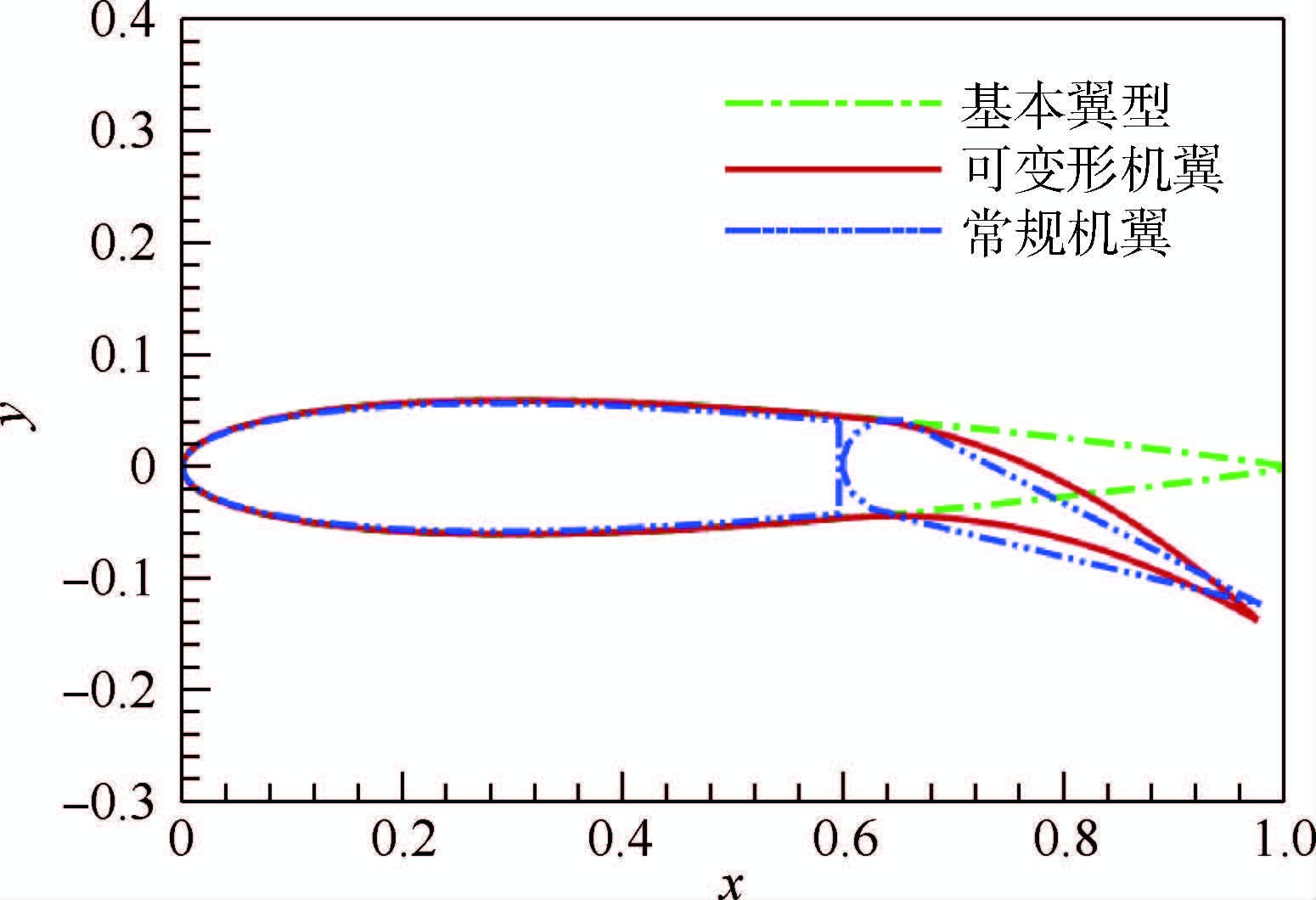 |
| 图 1 可变形机翼和常规机翼Fig. 1 Morphing wing and conventional wing |
| 图选项 |
2 数值计算方法本文数值计算中采用的基本方程为可压缩黏性常比热完全气体二维Navier-Stokes方程:
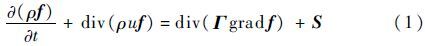
式中:f=[1 u v T]T $\Gamma ={{\left[\begin{matrix} 0 & \mu & \mu & \frac{k}{c} \\\end{matrix} \right]}^{T}}$
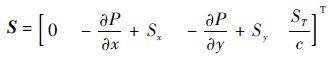
其中:ρ为气体密度;P为压强;u和v分别为x、y方向速度分量;μ为动力黏性系数;k为流体传热系数;c为比热容;T为绝对温度;S为广义源项,Si(i=x,y,T)为源项。
方程式(1)等号左端第2项为对流项,采用二阶迎风格式,等号右端第1项为扩散项,采用中心差分格式。通过有限体积法离散为差分方程,湍流模型采用Spalart-Allmaras(S-A)模型。流场网格为贴体结构网格,法向近壁面处的网格加密处理。材料为理想气体,远场采用压力远场边界条件,来流速度为0.1Ma,雷诺数Re约为2.3×106,翼型壁面采用无滑移固壁边界条件,采用求解压力耦合方程的半隐算法(SIMPLE)解上述问题。
图 2为使用上述计算方法得到的结果与实验结果[22]的对比,由图可以看出,升力系数CL和压力系数Cp分布与实验结果吻合较好,在升力系数较小时,阻力系数CD与实验结果基本吻合,随着升力系数的增大误差越来越大,但整体变化趋势相同。总体来看,模型的网格划分和所使用的计算方法是可靠的。
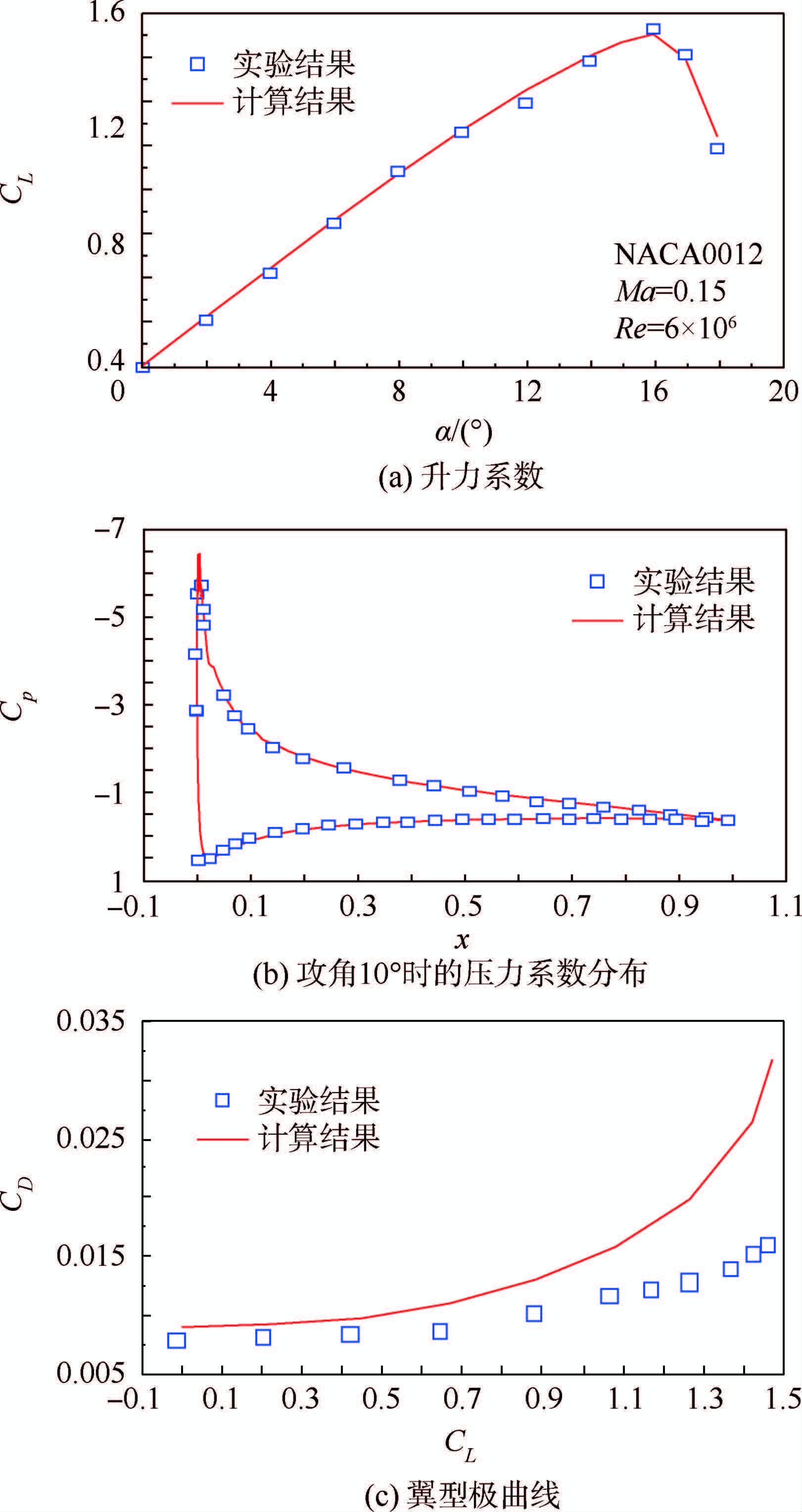 |
| 图 2 计算结果与实验结果对比Fig. 2 Comparison of computation results and experiment results |
| 图选项 |
3 计算结果3.1 可变形机翼与常规机翼气动特性对比在马赫数、雷诺数和后缘偏角β相同的条件下,对可变形机翼和常规机翼的气动特性进行数值研究,并对2种机翼的升阻特性和力矩特性进行对比分析。
后缘下偏10°时,可变形机翼与常规机翼的升力系数CL、力矩系数Cm、阻力系数CD和升阻比CL/CD随攻角的变化曲线如图 3所示。由图 3(a)看出,可变形机翼的失速攻角比常规机翼小,但两机翼的升力线斜率和最大升力系数基本一致。在失速前的攻角范围内,可变形机翼的升力系数比常规机翼的升力系数大,在攻角4°、8°和12°时,前者比后者分别提高了36.35%、21.84%和12.99%,提高的百分比随着攻角的增加而降低。在同一攻角下,可变形机翼的低头力矩系数明显大于常规机翼的低头力矩系数。攻角小于10°时,可变形机翼的阻力系数小于常规机翼的阻力系数;攻角大于10°时,可变形机翼的阻力系数明显大于常规机翼的阻力系数。由图 3(d)可以看出,2种机翼的升阻比均随着攻角的增加先升高后降低,可变形机翼的升阻比在攻角2°时达到最大值72.91,常规机翼的升阻比在攻角8°时达到最大值46.17;在攻角-10°~12°范围内,可变形机翼的升阻比明显优于常规机翼的升阻比。
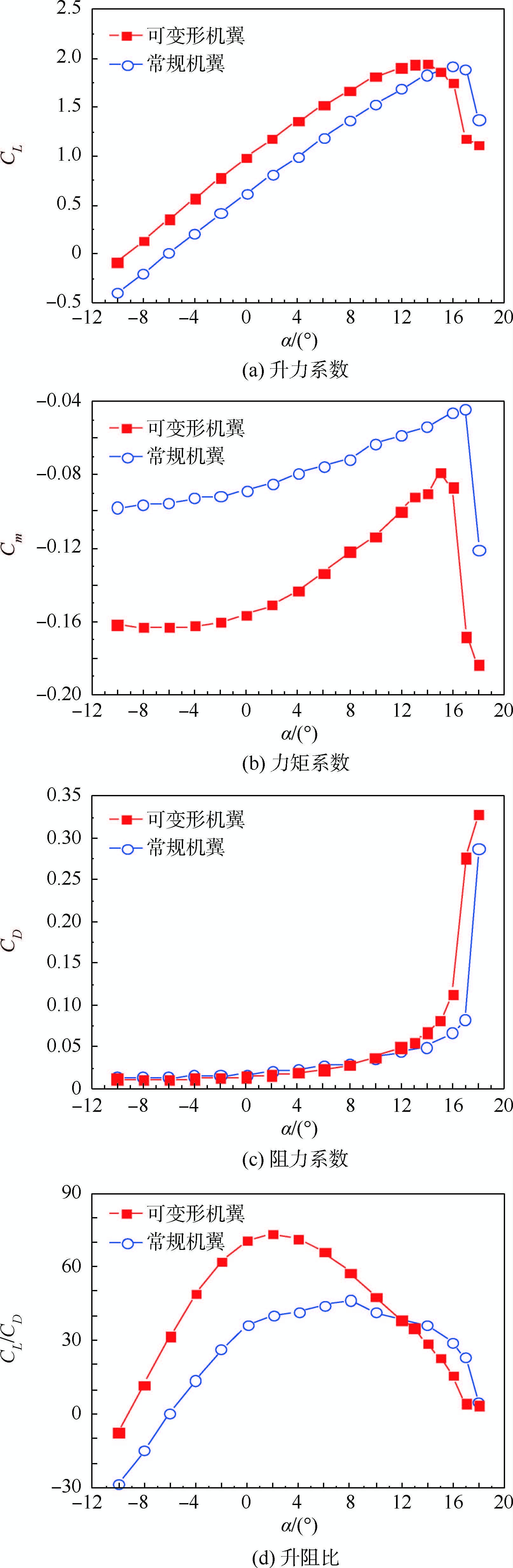 |
| 图 3 后缘下偏10°时两机翼气动系数对比Fig. 3 Comparison of aerodynamic coefficients of both wings for β=10° |
| 图选项 |
从机翼表面压力分布附近流场结构等方面研究上述气动特性产生机理。在攻角8°、12°和16°时,2种机翼的表面流线图和压力系数分布分别如图 4~图 6所示。
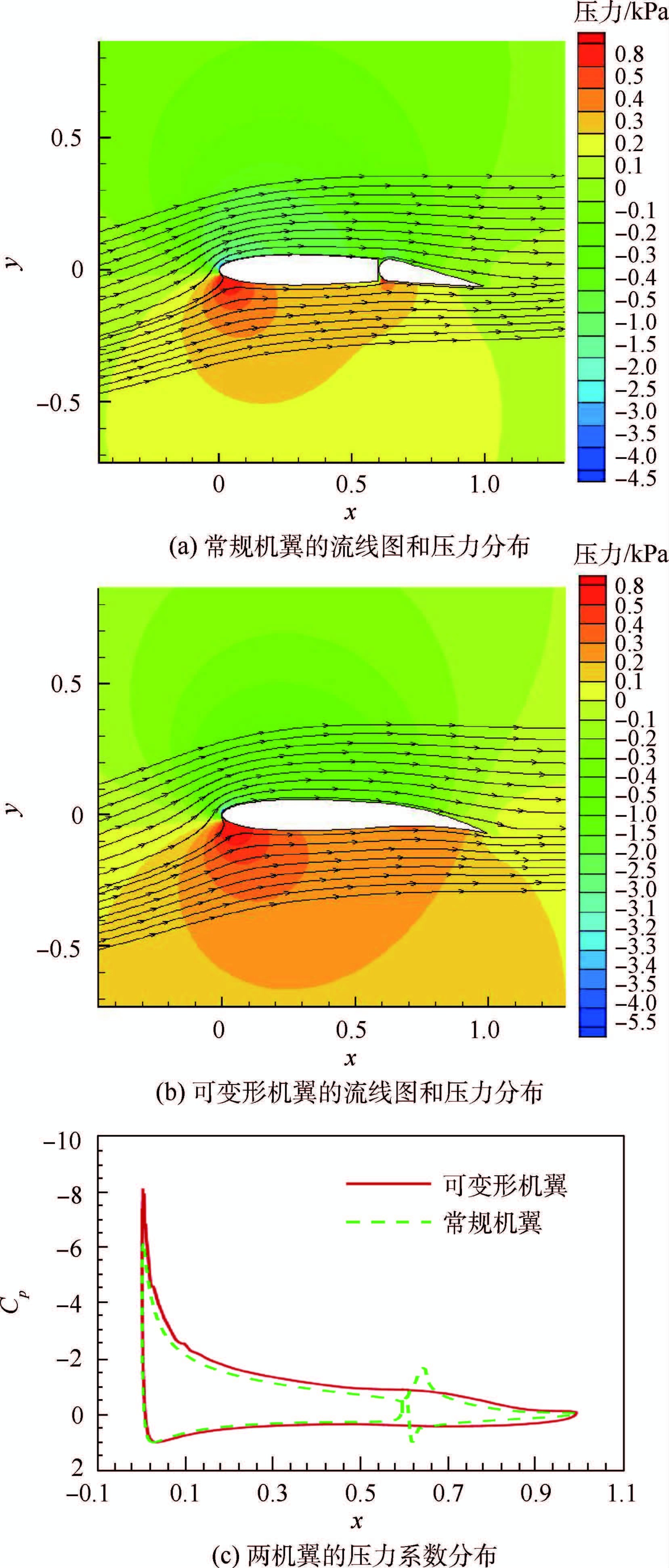 |
| 图 4 β=10°,α=8°时两机翼的流线图和压力系数Fig. 4 Streamlined diagrams and pressure coefficients of both wings for β=10°,α=8° |
| 图选项 |
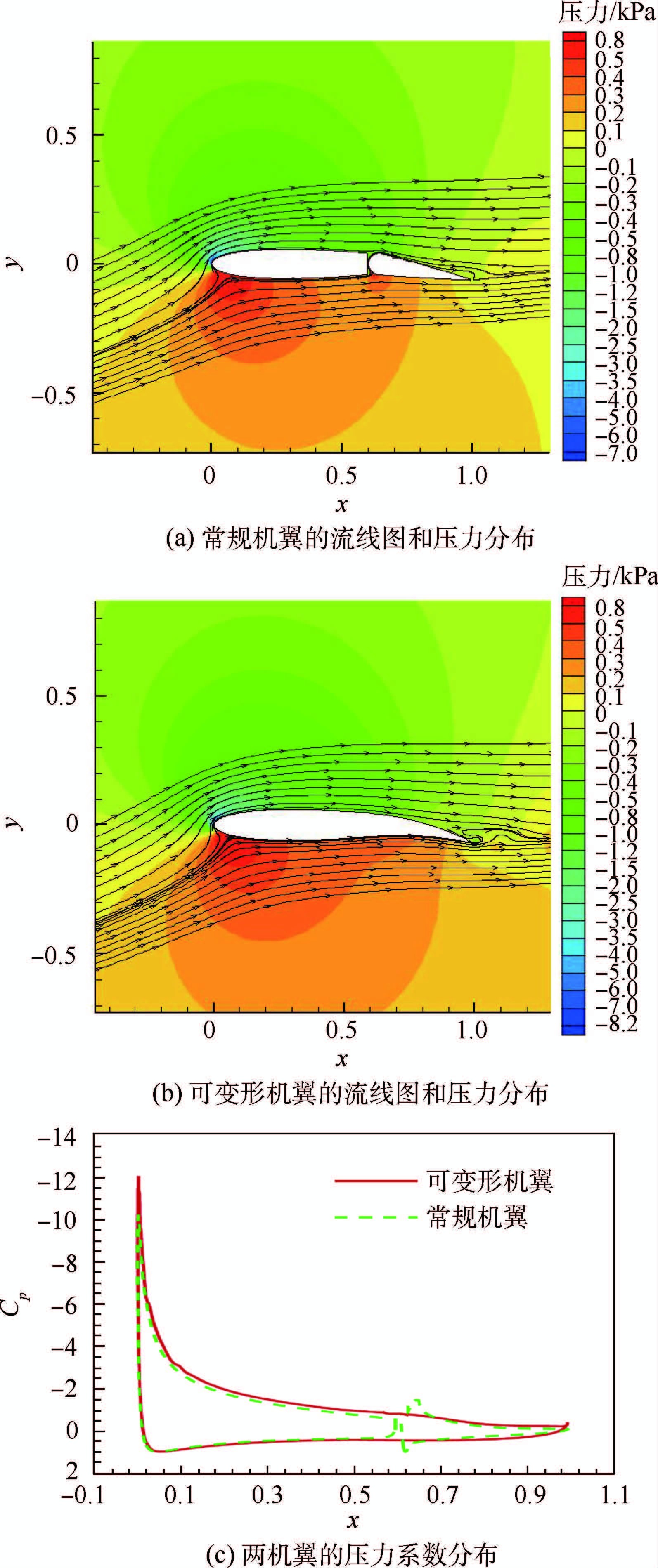 |
| 图 5 β=10°,α=12°时两机翼的流线图和压力系数Fig. 5 Streamlined diagrams and pressure coefficients of both wings for β=10°,α=12° |
| 图选项 |
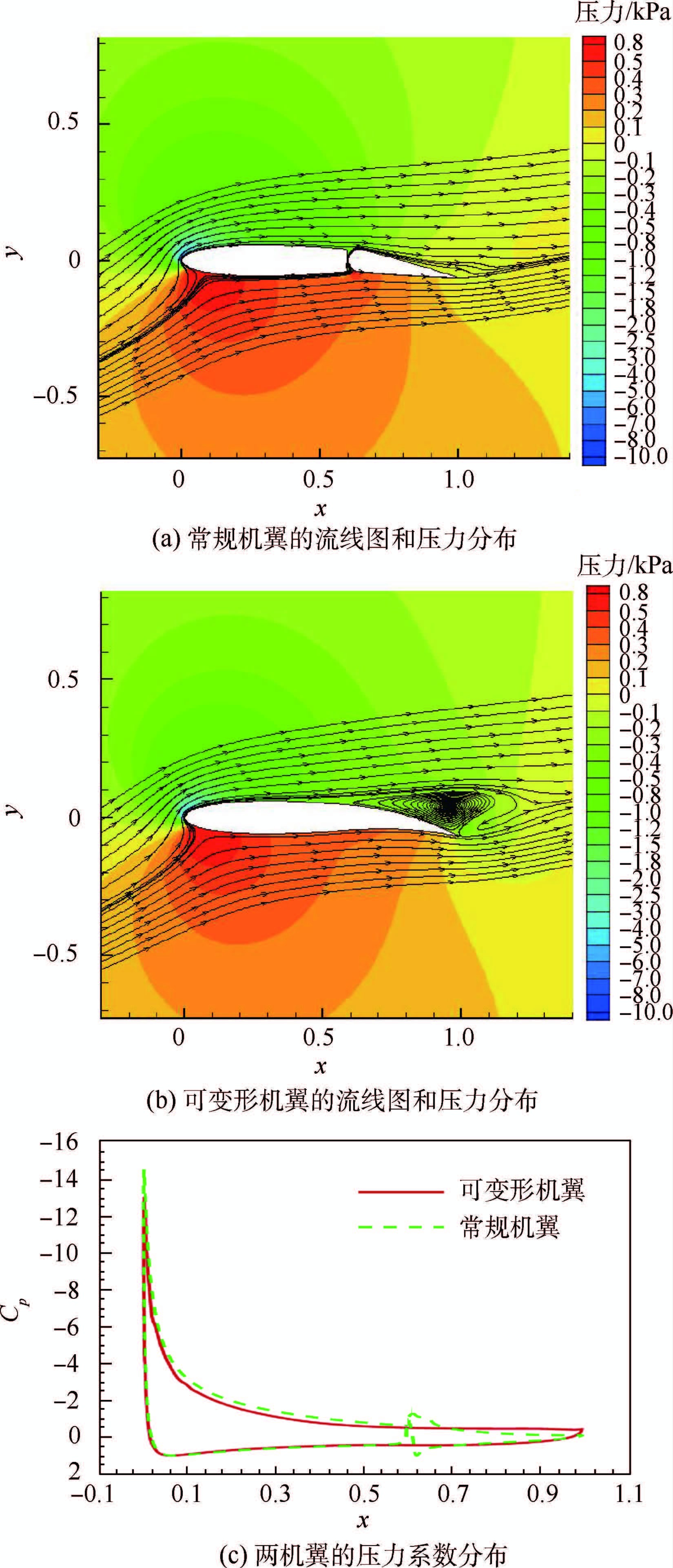 |
| 图 6 β=10°,α=16°时两机翼的流线图和压力系数Fig. 6 Streamlined diagrams and pressure coefficients of both wings for β=10°,α=16° |
| 图选项 |
在攻角8°时,可变形机翼和常规机翼的气流均平稳流过机翼后缘,没有流动分离。由压力系数分布看出,可变形机翼表面压力系数曲线平滑过渡,常规机翼表面压力系数曲线在襟翼前缘局部凸起,其主翼上表面的压力系数明显大于可变形机翼主翼上表面的压力系数。这样从整体上看,常规机翼上下表面压力系数围成的面积小于可变形机翼压力系数围成的面积,此时表现为可变形机翼的升力系数大于常规机翼的升力系数。
在攻角12°时,可变形机翼后缘已出现了较大流动分离,而常规机翼后缘只有很小的分离,可变形机翼较大的流动分离增加了阻力,升力较常规机翼增加的百分比与攻角8°时相比降低了8.84%。
攻角增大到16°,可变形机翼后缘的分离覆盖了整个后缘,已经完全失速,而常规机翼分离区很小。失速后可变形机翼的阻力迅速增加,同一攻角下远大于常规机翼的阻力。由压力系数分布看出,可变形机翼主翼上表面的压力系数明显大于常规机翼主翼上表面的压力系数。从整体上看,可变形机翼上下表面压力系数围成的面积小于常规机翼压力系数围成的面积,此时表现为常规机翼的升力系数大于可变形机翼的升力系数。
机翼后缘流动分离区大小不同引起了机翼表面压力分布不同,从而表现为升力系数、阻力系数、力矩系数的不同,也体现在升阻比的显著不同。从机翼变形方式看,可变形机翼表面无缝光滑连接,压力分布则平滑过渡,常规机翼贴近下表面的气流经缝隙流向上表面,使上表面的气流速度提高,因而襟翼前缘的压力分布出现了凸起。两机翼变形段范围一样,但襟翼的转轴点相对于柔性后缘的转轴点略靠后,偏转角度相等时,可变形机翼的后缘端点相对于常规机翼的后缘端点略偏左下方;且柔性后缘中弧线为抛物线,襟翼中弧线为直线,柔性后缘中弧线很大比例都在襟翼中弧线之上,因此可变形机翼的弯度比常规机翼的弯度大。由薄翼理论可知,靠近后缘端点的中弧线斜率越大,由弯度引起的攻角增量会越大。可变形机翼在后缘端点的中弧线斜率比常规机翼大,因此弯度引起的攻角增量较大,从而有效攻角较大,失速攻角较小,同一攻角的升力系数较大。
3.2 可变形机翼后缘大偏角的失速特性飞机起飞着陆时柔性后缘大角度下偏,若攻角较大,则易引发失速。因此,有必要对可变形机翼后缘大偏角时的失速特性进行研究。图 7给出了后缘不同偏角的升力系数变化曲线。
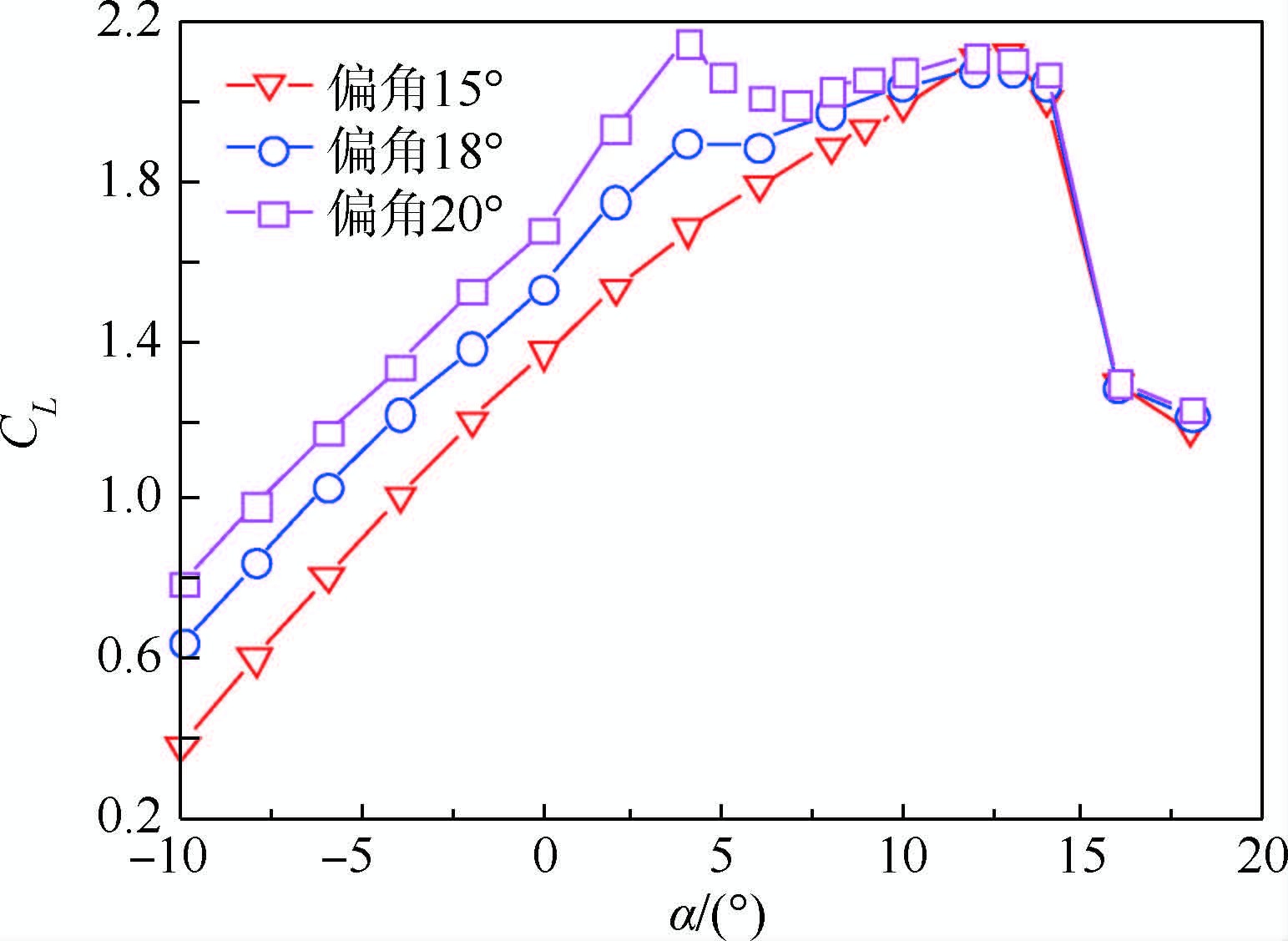 |
| 图 7 不同偏角的升力系数Fig. 7 Lift coefficients in different deflection angles |
| 图选项 |
后缘下偏15°时,升力系数随着攻角的增加而持续升高直至失速;下偏18°时,升力系数在攻角4°~6°范围内几乎无变化,而后随着攻角的增加而缓慢升高直至失速;下偏20°时,升力系数在攻角4°~7°范围内持续下降,而后随着攻角的增加而缓慢升高,在整个攻角范围内,升力系数曲线出现了2次峰值,第1次在攻角4°,第2次在攻角12°。后缘下偏15°的失速攻角为13°,下偏20°的失速攻角为4°。可以看出,随着下偏角度的增加,失速攻角有变小趋势,这是因为下偏角度越大,机翼弯度越大,有效攻角越大,从而实际失速攻角越小。
对于可变形机翼后缘下偏20°时升力系数出现2次峰值的现象,可以从机翼表面流场及压力分布的角度研究其流动机理。图 8给出了可变形机翼不同攻角的机翼表面流线图,图 9给出了不同攻角的压力系数分布。
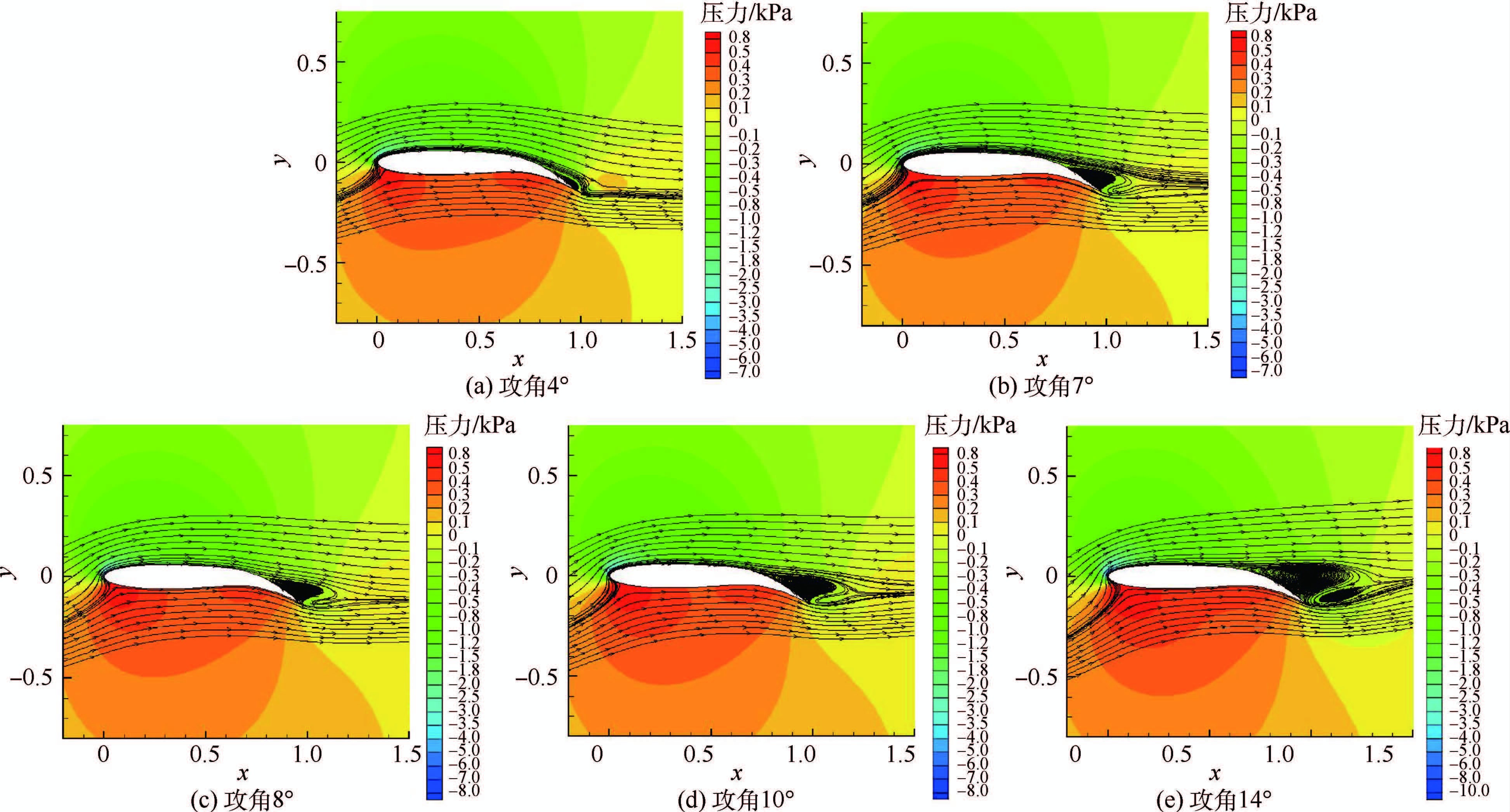 |
| 图 8 后缘下偏20°时可变形机翼不同攻角的流线图和压力分布Fig. 8 Streamlined diagrams and pressure contours of morphing wing at different angles of attack for β=20° |
| 图选项 |
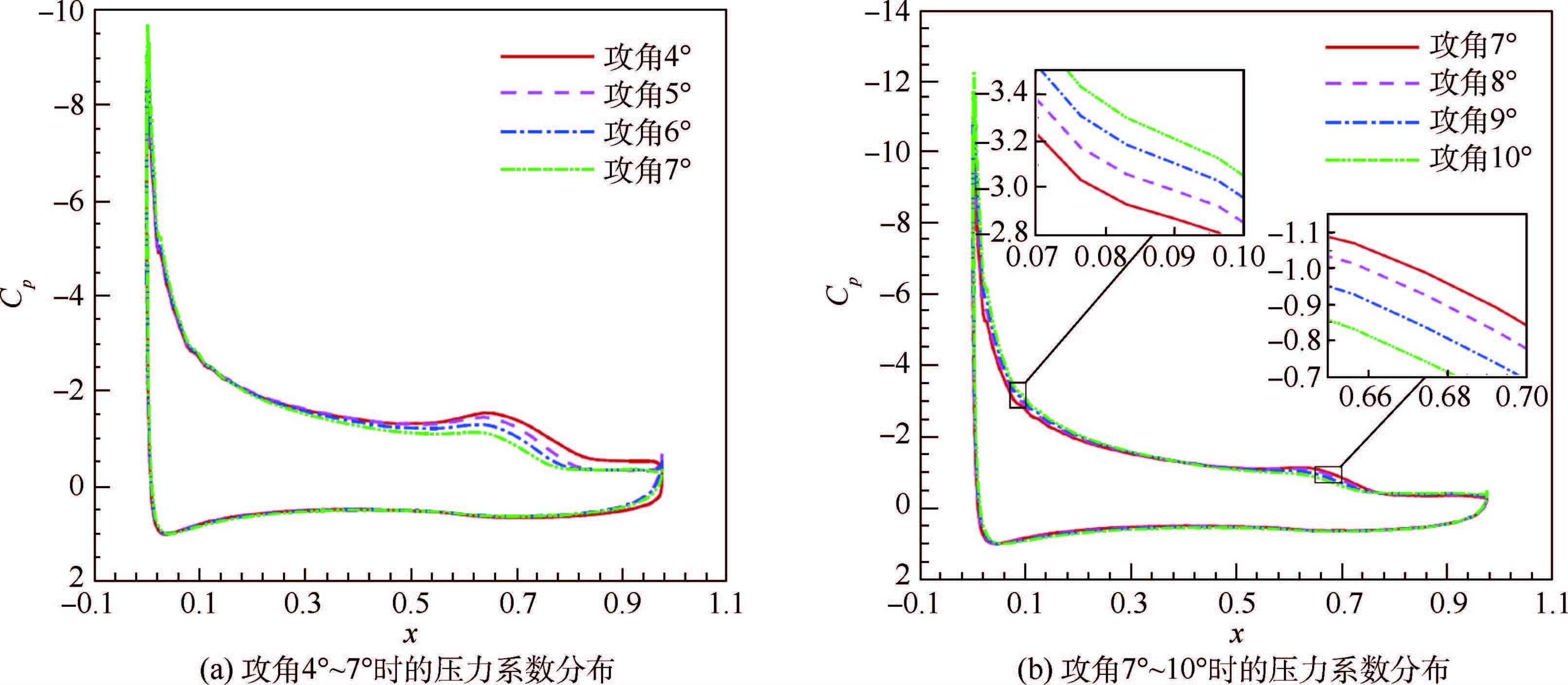 |
| 图 9 后缘下偏20°时可变形机翼的压力系数Fig. 9 Pressure coefficients of morphing wing for β=20° |
| 图选项 |
在攻角4°~7°范围内,机翼后缘已经产生了分离,且分离区域随着攻角的增加逐渐向前扩展,如图 8(a)和图 8(b)所示。由图 9(a)看出,随着攻角的增加,主翼前缘的吸力峰值在升高,而后缘上翼面压力系数在变大。在这期间,因后缘分离区的扩大引起的升力损失量大于因攻角的增加引起的升力增量,整体上表现为升力系数随着攻角的增加而降低。在攻角8°~10°范围内,后缘分离涡不再进一步向前扩展,分离区域基本不变,如图 8(c)和图 8(d)所示。
由图 9(b)看出,随着攻角的增加,主翼前缘的吸力峰值在升高,而后缘压力系数变化并不明显。在这期间,因攻角的增加引起的升力增量大于因后缘分离引起的升力损失量,整体上表现为升力系数随着攻角的增加而升高,但此时已有较大的流动分离,升力系数的增长比线性段缓慢。攻角大于12°时,后缘的分离区域进一步向前扩展,如图 8(e)所示,此后升力系数随着攻角的增加而降低。
由此可以看出,后缘大角度下偏,当后缘产生流动分离时,后缘涡的扩展引起的升力损失量大于因攻角的增大引起的升力增量,升力系数呈现下降趋势;反之,后缘涡的扩展引起的升力损失量小于因攻角的增大引起的升力增量,升力系数呈现升高趋势。
从可变形机翼变形方式看,后缘的中弧线为抛物线,大角度下偏时,越靠近后缘中弧线斜率越大,这样就使得后缘的分离不易往前传,对流动分离起到控制作用,从而失速后维持了升力的再次增加,具有较好的失速特性。
4 结 论本文采用可压缩Navier-Stokes方程和S-A湍流模型对可变形机翼进行气动特性研究,并与常规带缝隙的机翼作对比,研究发现:
1) 后缘下偏时,可变形机翼的失速攻角小于常规机翼,但两者的升力线斜率和最大升力系数基本一致。在发生失速之前,可变形机翼的升力系数和升阻比明显高于常规机翼,但产生的低头俯仰力矩相对较大。
2) 可变形机翼后缘大角度下偏时,升力系数随着攻角的增加先升高后降低,而后又随着攻角的增加而升高直至完全失速,呈现出二次上升现象。
3) 可变形机翼后缘下偏时,靠近后缘端点处的中弧线斜率增大到一定值,可以抑制后缘涡的前传,在失速后维持升力的再次增加,增大了有效攻角范围,具有较好的失速特性。
参考文献
| [1] | RODRIGUEZ A R.Morphing aircraft technology survey[C]//45th AIAA Aerospace Sciences Meeting 2007.Reston:AIAA,2007,21:15064-15079. |
| [2] | WEISSHAAR T A.Morphing aircraft systems:Historical perspectives and future challenges[J].Journal of Aircraft,2013,50(2):337-353. |
| Click to display the text | |
| [3] | 高彦峰.可变形翼型的非定常气动特性研究[D].合肥:中国科学技术大学,2012:5. GAO Y F.Study on the unsteady aerodynamics characteristics for the morphing airfoil[D].Hefei:University of Science and Technology of China,2012:5(in Chinese). |
| Cited By in Cnki (1) | |
| [4] | MONNER H P, SACHAU D,BREITBACH E.Design aspects of the elastic trailing edge for an adaptive wing:Report ADP10488[R].Neuilly-sur-Seine:RTO,1999:14.1-14.8. |
| [5] | AHMED S, GUO S J.Optimal design and analysis of a wing with morphing high lift devices[C]//AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2013. |
| Click to display the text | |
| [6] | VASISTA S, TONG L Y,WONG K C.Realization of morphing wings:A multidisciplinary challenge[J].Journal of Aircraft,2012,49(1):11-28. |
| Click to display the text | |
| [7] | DI MATTEO N, GUO S J,AHMED S.Design and analysis of a morphing flap structure for high lift wing[C]//51st AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Material Conference.Reston:AIAA,2010. |
| [8] | DI MATTEO N, GUO S J,LI D.Morphing trailing edge flap for high lift wing[C]//52nd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Material Conference.Reston:AIAA,2011. |
| Click to display the text | |
| [9] | YOKOZEKI T, SUGIURA A.Development of variable camber morphing airfoil using corrugated structure[J].Journal of Aircraft,2014,51(3):1023-1029. |
| Click to display the text | |
| [10] | 尹维龙, 石庆华,田冬奎.变体后缘的索网传动机构设计与分析[J].航空学报,2013,34(8):1824-1831. YIN W L,SHI Q H,TIAN D K.Design and analysis of transmission mechanism with cable networks for morphing trailing edge[J].Acta Aeronautica et Astronautica Sinica,2013,34(8):1824-1831(in Chinese). |
| Cited By in Cnki (2) | |
| [11] | ON W C,GOMES A A, SULEMAN A.Optimal design of a morphing airfoil using spectral level set methodology[C]//6th World Congress on Structural and Multidisciplinary Optimization.Rio de Janeiro:[s.n.],2005. |
| [12] | URNES J, NGUYEN N.A mission adaptive variable camber flap control system to optimize high lift and cruise lift-to-drag ratios of future N+3 transport aircraft[C]//51st AIAA Aerospace Sciences Meeting.Reston:AIAA,2013. |
| Click to display the text | |
| [13] | URNES J M,MORRIS C, SHEAHAN J,et al.Control system design for a variable camber continuous trailing edge flap system on an elastic wing[C]//55th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2014. |
| Click to display the text | |
| [14] | IPPOLITO C, NGUYEN N,TOTAH J.Initial assessment of a variable-camber continuous trailing-edge flap system on a rigid wing for drag reduction in subsonic cruise[C]//AIAA Infotech Aerospace Conference.Reston:AIAA,2013. |
| [15] | LAMBIE B, KRENIK A,TROPEA C.Numerical simulation of an airfoil with a flexible trailing edge in unsteady flow[C]//51st AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2010. |
| Click to display the text | |
| [16] | STEENHUIZEN D, TOOREN M V.The implementation of a knowledge-based framework for the aerodynamic optimization of a morphing wing device[J].Advanced Engineering Informatics,2012,26(2):207-218. |
| Click to display the text | |
| [17] | 杨智春, 解江.柔性后缘自适应机翼的概念设计[J].航空学报,2009,30(6):1028-1034. YANG Z C,XIE J.Concept design of adaptive wing with flexible trailing edge[J].Acta Aeronautica et Astronautica Sinica,2009,30(6):1028-1034(in Chinese). |
| Cited By in Cnki (18) | |
| [18] | 解江, 杨智春,党学会.柔性后缘自适应机翼气动特性和操纵反效特性的比较分析[J].工程力学,2009,26(10):245-251. XIE J,YANG Z C,DANG X H.Comparative study on aerodynamics and control reversal characteristics of adaptive wings with flexible trailing edge[J].Engineering Mechanicals,2009,26(10):245-251(in Chinese). |
| Cited By in Cnki (4) | |
| [19] | 陈钱, 白鹏,尹维龙,等.可连续光滑偏转后缘的变弯度翼型气动特性分析[J].空气动力学学报,2010,28(1):46-53. CHEN Q,BAI P,YIN W L,et al.Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J].Acta Aerodynamica Sinica,2010,28(1):46-53(in Chinese). |
| Cited By in Cnki (22) | |
| [20] | KAUL U K, NGUYEN N T.Drag optimization study of variable camber continuous trailing edge flap using overflow[C]//32nd AIAA Applied Aerodynamics Conference.Reston:AIAA,2014. |
| Click to display the text | |
| [21] | KRZYSIAK A, NARKIEWICZ J.Aerodynamic loads on airfoil with trailing-edge flap pitching with different frequencies[J].Journal of Aircraft,2006,43(2):407-418. |
| Click to display the text | |
| [22] | RUMSEY C L. 2D N00:2D NACA 0012 airfoil validation case[EB/OL].Langley Research Center,2014(2014-12-18)[2014-01-05].http://turbmodels.larc.nasa.gov/naca0012_val.html. |
| Click to display the text |
