?故障模式及影响分析(Failure Mode and Effects Analysis,FMEA)是一种分析系统中每个产品潜在的故障模式及其对系统造成的影响,并按每一种故障模式的发生概率(Occurrence,O)、严重程度(Severity,S)和检测难易程度(Detection,D)予以分类的归纳分析方法^[1]。传统的FMEA采用风险优先数(Risk Priority Number,RPN)来表示故障模式造成的影响即风险水平的高低,从而有针对性地提出预防或改进措施,以保证系统的可靠性。每个影响因素(O、S和D)有10个等级,RPN值由3个影响因素的等级数相乘确定,RPN值越大,说明该故障模式的风险水平越高,对系统的危害性越大^[2]。但传统的FMEA方法在实践中存在以下问题^[3]:
1) 影响因素(O、S和D)相邻等级之间差距很小,评估人员很难判定其所属等级数。
2) 传统FMEA没有考虑影响因素各自的权重,如对于不可修复系统来说,发生概率O是关键的影响因素,其权重不能与严重程度S和检测难易程度D等同。
3) RPN值的计算方法存在一定的争议,因为一个影响因素很小的变动,可能造成RPN值相差很大。如2个故障模式的O、S和D等级数分别为1、9、9和2、9、9,则它们的RPN值分别为81和162,相差2倍,但由于是发生概率的微小不同,可能对系统的危害相差不大。
为解决传统FMEA存在的缺陷,国内外****提出了很多改进方法。Pillay和Wang^[3]引入模糊规则库和灰色关联理论对风险水平不同但RPN值相同的故障模式进行分级,并运用去模糊语义值和灰色关联度确定最终的排序。Wang等^[4]提出了模糊RPN的分析方法,通过模糊语言对每一个故障模式的影响因素进行评价,并使用模糊加权几何平均法对RPN进行计算。Gargama和Chaturvedi^[5]也采用模糊语言变量表示评价专家对3个影响因素的评价,并通过匹配程度来评估评价信息与模糊数的匹配情况,应用alpha水平集来计算模糊RPN。Chin等^[6]考虑评估信息的不确定性,采用模糊证据推理对故障模式的影响因素进行评估,对各故障模式的风险水平排序时未考虑各影响因素的权重。Liu等^[7]提出了基于模糊证据推理和灰色理论的FMEA方法,但在确定影响因素权重时未考虑影响因素本身的客观信息。Garcia和Schirru^[8]利用模糊数据包络分析理论对故障模式的风险水平进行排序。王贵宝等^[9]利用于信息熵定理和最大信息熵推论,研究了影响因素和权重分配问题,提出了风险可能数。逼近理想解排序法(Technique for Order Preference by Similarity to Ideal Solution,TOPSIS)作为一种多指标综合评价的排序方法,在FMEA中也得到了应用发展。Kutlu和Ekmekciogˇlu^[10]将模糊理论与TOPSIS相结合对FMEA进行分析,并使用模糊层次分析法(Analytical Hierarchy Process,AHP)分配影响因素的权重,但模糊AHP确定权重时,一方面影响因素的权重相对比较时存在不确定性,不利于评价专家评定,另一方面也忽略了影响因素本身存在的客观信息。Braglia等^[11]也引入TOPSIS对FMEA中风险优先数进行分析,并举例验证了该方法的实用性,但未解决各影响因素评价中存在模糊性问题。
综合以上研究,本文将模糊证据推理和TOPSIS相结合,提出了模糊TOPSIS的FMEA方法。既解决了影响因素难以评价的问题,又通过TOPSIS的相对贴近度避免了传统FMEA中影响因素相乘带来的缺陷。此外,通过主观赋权法和客观赋权法相结合的方法来分配各影响因素的权重,不仅融合了评价专家的经验知识,而且考虑了影响因素本身的客观信息,使得权重分配更加合理。
1 提出的FMEA方法1.1 模糊置信结构设模糊语言变量H_ii(i=1,2,…,5)构成的评价集为:H={H₁₁,H₂₂,H₃₃,H₄₄,H₅₅}={VL,L,M,H,VH}^[11],其中：VL表示很低；L表示低；M表示中；H表示高；VH表示很高。模糊语言变量对各影响因素的评定准则及对应的模糊数如表 1所示^[3]。
表 1 模糊语言变量的评定准则及对应的模糊数Table 1 Evaluation standards of fuzzy linguistic terms and their fuzzy scores

评价等级	发生概率O评定准则	严重程度S评定准则	检测难易程度D评定准则	模糊数
VL	几乎不会发生故障	对设备运行几乎无影响	可根据故障现象直接断定	(0,1,1,2)
L	较少发生故障	需维修,但不影响设备性能	简单的检查可发现故障	(1,2,3,4)
M	偶尔发生故障,接下来会偶尔发生的故障	设备性能下降,但可以运行	经现行检测技术才可发现故障	(3,4,6,7)
H	有时候发生,接下来会反复发生的故障	设备性能基本丧失,无法运行	经现行检测技术较难发现故障	(6,7,8,9)
VH	经常发生,接下来必然发生的故障	引起人员伤亡或设备严重损坏	现行检测技术无法发现故障	(8,9,10,10)

表选项


设评估小组中有K名评价人员(T₁,T₂,…,T_k,…,T_K)对N个故障模式(F_M1,F_M2,…,F_Mn…,F_MN)关于O、S和D这3个影响因素(分别用E_F1、E_F2和E_F3表示)进行评价,用{(H_ij,α_ij^k(F_Mn,E_Fl))}(i＞j;i=1,2,…,5;j=1,2,…,5;k=1,2,…,K;n=1,2,…,N;l=1,2,3)表示评价结果,这种表示形式称为模糊置信结构,α_ij^k(F_Mn,E_Fl)为相对应的置信度^[12]。
1) 如评价等级“L”可表示为{(H₂₂,1.0)}。
2) 如果评价中认为“VL”可能性为40%,“L”可能性为60%,可用{(H₁₁,0.4),(H₂₂,0.6)}表示;如果置信度之和不为1,如{(H₁₁,0.3),(H₂₂,0.6)},丢失的10%为局部无法评价,可分配到“VL”到“VH”的任何等级。
3) 当无法确定置信度时,如认为某影响因素在“VL”到“L”之间时,可用{(H₁₂,1.0)}表示。
用${{\tilde{x}}_{n}}$={(H_ij,α_ij(F_Mn,E_Fl))}表示所有评价人员对故障模式F_Mn的影响因素E_Fl评价的综合,称为综合置信结构,对应置信度的计算公式为
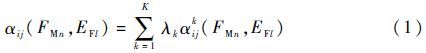
式中:λ_k为评价人员的权重,$\sum\limits_{k=1}^{K}{{{\lambda }_{k}}}=1$。
1.2 建立明确置信矩阵根据综合置信结构${{\tilde{x}}_{n}}$,通过反模糊化和加权平均的方法建立明确置信矩阵。Chen和Klein^[13]提出了一种简便的去模糊化方法,即
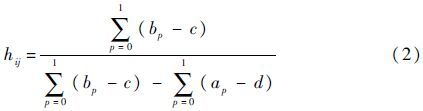
式中:h_ij为H_ij去模糊化后的明确值。
由模糊语言变量的模糊数知c=0,d=10,其余参数取值如图 1所示,按式(2)将各模糊评价等级去模糊化后明确值如表 2所示。

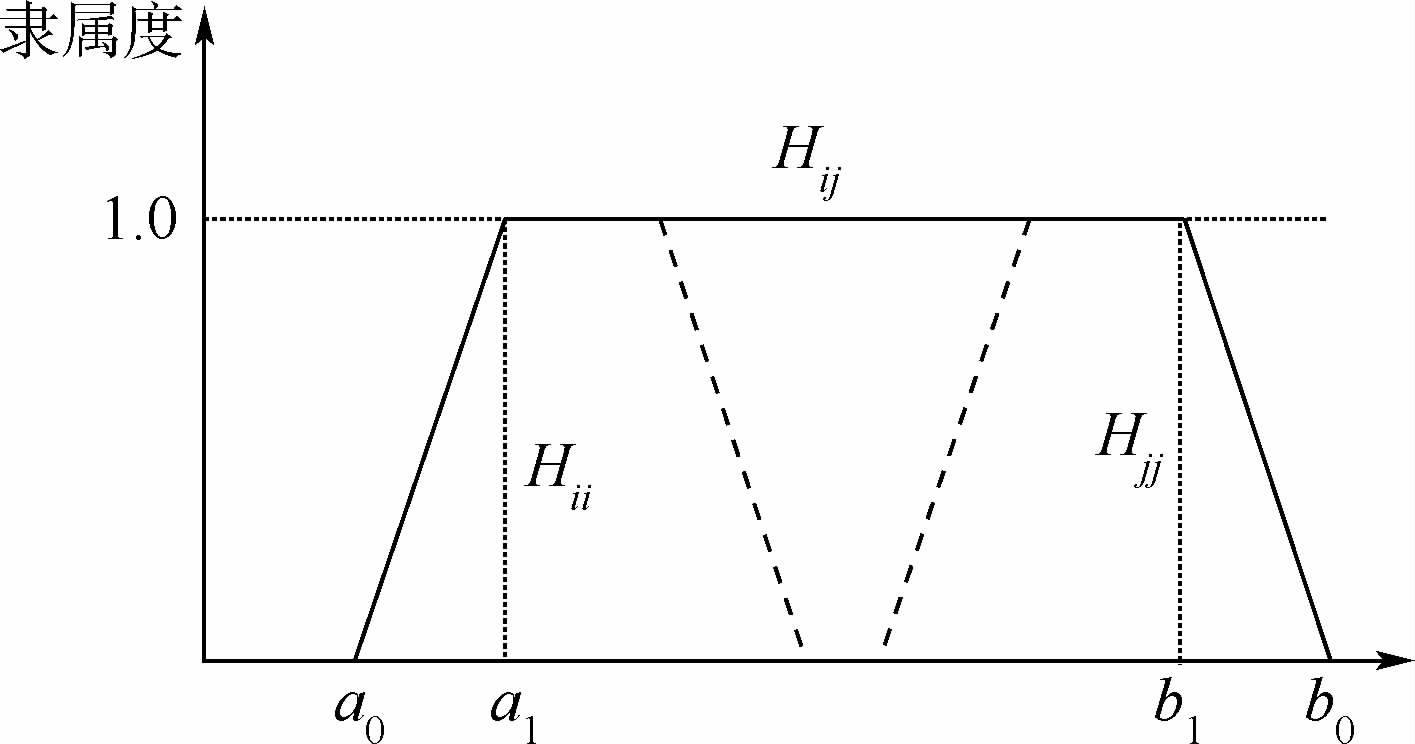图 1 评价等级去模糊化Fig. 1 Defuzzification of evaluation grade

图选项

表 2 各评价等级的明确值Table 2 Clear values of evaluation grades

评价等级	hij	评价等级	hij	评价等级	hij
H11	0.130	H12	0.295	H24	0.500
H22	0.292	H13	0.394	H25	0.541
H33	0.500	H14	0.459	H34	0.567
H44	0.708	H15	0.500	H35	0.606
H55	0.870	H23	0.433	H45	0.741

表选项


故障模式F_Mn关于影响因素E_Fl的明确值,可由式(3)加权平均得到:
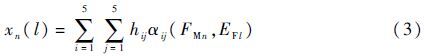
那么,所有x_n(l)构成明确置信矩阵:
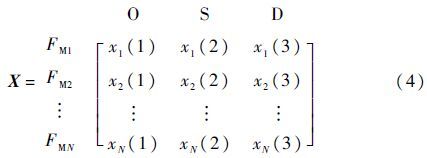
1.3 建立加权规范化矩阵首先,对明确置信矩阵用向量规范化法构造规范化矩阵^[14]:
式中:。
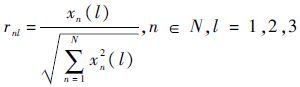然后,构建加权规范化矩阵:
式中:z_nl=w_lr_nl。
由于各影响因素的权重w_l是FMEA分析的关键。本文将主观赋权法和客观赋权法相结合分配各权重,主观赋权法采用专家评价的方法,客观赋权法采用熵权法。
1) 主观赋权法计算影响因素权重
对各权重的评价如第1.1节和第1.2节所述。但在构建模糊置信矩阵时,其模糊语言变量对应的模糊数不同,影响因素权重的评价等级及对应的模糊如表 3所示^[4]。
表 3 影响因素权重的评价等级及对应的模糊数Table 3 Evaluation grades of effect factor’s weights and their fuzzy scores

评价等级	模糊数
非常重要	(0,0,0.25)
重要	(0,0.25,0.5)
中	(0.25,0.5,0.75)
次要	(0.5,0.75,1)
非常次要	(0.75,1,1)

表选项


设w_l^S(l=1,2,3)为计算得到的明确置信矩阵,为使得权重之和为1,按式(7)将其归一化,得到主观赋权法分配的影响因素权重w_l^S(l=1,2,3)。
2) 客观赋权法计算影响因素权重
熵权法是根据多属性决策问题中的数据确定信息熵,信息熵越小,信息的无序度越低,其信息的效用值越大,影响因素的权重越大。因此,熵权法是一种客观赋权法,其完全取决于数据,计算过程如下^[15]。
定义第l个影响因素的熵为
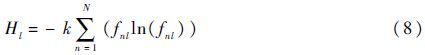
式中:
其中：n=1,2,…,N,N为故障模式的总数；l=1,2,3。
确定熵权,即各影响因素的权重为
3) 综合度量各影响因素的权重
采用合成的方法将主、客观2种权重结合起来。常见的合成方法有线性加权合成法、乘法合成法、混合法和代换法^[16]。由于各影响因素权重的数值差距较大,本文采用乘法合成法来综合度量各影响因素的权重,即
1.4 计算相对贴近度首先,确定正理想解A⁺和负理想解A^-:
式中:
其次,采用欧氏距离公式计算各故障模式到正理想解和负理想解的距离:
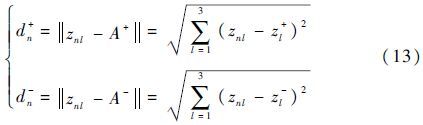
然后,计算各故障模式的相对贴近度C_n:
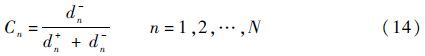
最后,根据相对贴近度递减顺序对各故障模式的风险水平进行排序,排序最前的便是对系统危害性最大的。
2 实例应用本文以数控系统为例,检验该FMEA方法的可行性和有效性。根据文献^[17]可知数控系统的主要故障模式为:线路、电缆短路(F_M1),线路、电缆断路(F_M2),元器件损坏(F_M3),元器件松动(F_M4),过载(F_M5),操作系统失灵(F_M6),可编程逻辑控制器(PLC)控制模块失调(F_M7),计算机数字控制机床(CNC)参数设定错误(F_M8),程序丢失(F_M9)。对数控系统进行FMEA时,其评估小组涵盖设计、制造、运行和维修等不同部门专家,文献^[18]考虑不同评价人员的职称、工龄、学历和年龄不同导致的知识经验不同,计算得出各评价人员权重λ_k分别为:0.10,0.30,0.25,0.15,0.20。该FMEA方法在数控系统中的分析过程如下:
1) 用模糊置信结构表示评价人员对所有故障模式影响因素的评价,见表 4。
表 4 所有故障模式影响因素的评价信息Table 4 Evaluation information of all failure modes’ effect factors

影响因素	Ti	故障模式
		FM1	FM2	FM3	FM4	FM5	FM6	FM7	FM8	FM9
O	T1	H33	(H13,1.0)	(H45,0.9)	H44	(H34,1.0)	(H33,0.9)(H44,0.1)	H44	(H22,0.8)(H33,0.2)	H22
	T2	H33	H22	H55	(H33,0.8)	(H34,1.0)	(H34,1.0)	H44	(H22,0.9)	H22
	T3	(H34,1.0)	(H34,1.0)	(H44,0.8)(H55,0.2)	H33	H22	H33	(H25,0.9)	H33	H11
	T4	H33	(H12,1.0)	H44	(H33,0.8)(H44,0.2)	(H34,1.0)	H33	(H34,1.0)	H22	(H12,1.0)
	T5	H33	H22	H55	H33	H22	H33	H44	(H12,0.9)	(H12,0.8)
S	T1	H22	(H12,1.0)	H44	(H14,1.0)	H33	(H15,1.0)	(H24,0.9)	(H13,0.9)	H22
	T2	H33	H22	H44	H33	(H23,1.0)	H33	(H45,0.9)	H22	H11
	T3	H22	(H12,1.0)	H44	H33	H22	(H34,0.9)	H44	H33	(H12,1.0)
	T4	H33	H22	H44	(H22,0.9)	H33	H33	H33	(H23,1.0)	H11
	T5	H22	H22	(H45,1.0)	H33	H22	H33	H44	H22	H22
D	T1	H22	H22	H22	H22	(H12,1.0)	H22	H22	(H13,1.0)	H12
	T2	H33	(H12,1.0)	(H12,1.0)	H22	H22	(H23,1.0)	(H13,1.0)	H22	H11
	T3	(H13,1.0)	(H12,1.0)	(H11,0.7)(H22,0.3)	(H23,0.9)	H22	H22	H22	H22	(H12,0.2)(H22,0.8)
	T4	H22	H22	H22	(H23,1.0)	(H12,1.0)	H33	(H23,1.0)	H22	H22
	T5	H33	(H12,1.0)	(H12,1.0)	H22	H22	H22	(H22,0.7)(H23,0.3)	(H12,1.0)	(H12,1.0)

表选项


2) 结合表 2和表 4,按式(1)和式(3)建立明确置信矩阵,见表 5。
表 5 各影响因素的明确置信矩阵Table 5 Clear belief matrix of all effect factors

故障模式	O	S	D
FM1	0.517	0.386	0.422
FM2	0.371	0.293	0.294
FM3	0.798	0.715	0.265
FM4	0.527	0.465	0.350
FM5	0.443	0.386	0.293
FM6	0.522	0.453	0.366
FM7	0.635	0.517	0.352
FM8	0.359	0.376	0.303
FM9	0.253	0.220	0.244

表选项


3) 根据式(5)将明确置信矩阵用向量规范化法构造规范化矩阵,见表 6。
表 6 各影响因素的规范化矩阵Table 6 Normalized matrix of all effect factors

故障模式	O	S	D
FM1	0.112	0.084	0.187
FM2	0.058	0.048	0.091
FM3	0.267	0.288	0.074
FM4	0.116	0.122	0.129
FM5	0.082	0.084	0.090
FM6	0.114	0.116	0.141
FM7	0.169	0.151	0.130
FM8	0.054	0.080	0.096
FM9	0.027	0.027	0.063

表选项


4) 确定各影响因素的权重
首先,用主观赋权法确定各影响因素的权重:评价人员对各影响因素权重的评价信息见表 7;同本节1)和2),可得到明确置信矩阵(w₁^S,w₂^S,w₃^S)=(0.660,0.214,0196);根据式(7)将其归一化得:(w₁^S,w₂^S,w₃^S)=(0.617,0.200,0.183)。
表 7 各影响因素权重的评价信息Table 7 Evaluation information of effect factor’s weights

Ti	O	S	D
T1	{H44,1.0}	{H22,0.6}{H33,0.4}	{H11,1.0}
T2	{H45,1.0}	{H33,1.0}	{H22,1.0}
T3	{H33,0.4}{H44,0.6}	{H34,1.0}	{H22,1.0}
T4	{H45,1.0}	{H33,1.0}	{H11,1.0}
T5	{H33,0.9}	{H23,1.0}	{H12,1.0}

表选项


然后,根据式(8)~式(10)可得客观赋权法确定的权重为w_l^O=(0.424,0.448,0.128)。
最后,按式(11)计算综合度量后各影响因素的权重为w_l=(0.698,0.239,0.063)。
5) 根据式(6)和式(12)～式(14)可得各故障模式到正理想解和负理想解的距离d_i⁺、d_i^-、相对贴近度C_i和C_i排序如表 8所示。
表 8 各故障模式的d_i⁺、d_i^-、C_i和C_i排序Table 8 d_i⁺、d_i^-、C_i and rank of C_i for all failure modes

故障模式	di+	di-	Ci	排序
FM1	0.118	0.061	0.341	5
FM2	0.157	0.022	0.122	8
FM3	0.007	0.178	0.960	1
FM4	0.112	0.066	0.371	3
FM5	0.138	0.041	0.228	6
FM6	0.114	0.064	0.361	4
FM7	0.076	0.103	0.577	2
FM8	0.157	0.022	0.125	7
FM9	0.179	0.001	0.003	9

表选项


根据C_i排序得出数控系统各故障模式的风险水平从高到低的排序为:F_M3>F_M7>F_M4>F_M6>F_M1>F_M5>F_M8>F_M2>F_M9,可以看出风险水平最高的是元器件损坏,对数控系统的危害性最大,其次是PLC控制模块失调,危害性最小的是程序丢失。
为了验证本文所提FMEA方法的优越性,采用传统的FMEA方法进行对比。传统FMEA方法采用RPN值来表示各故障模式风险水平的高低,其对数控系统的分析结果如表 9所示,根据RPN值大小进行各故障模式风险水平的排序为F_M3>F_M7>F_M4>F_M6>F_M1=F_M5>F_M8>F_M2=F_M9。通过结果可以看出,传统FMEA方法分析得到的故障模式F_M1(线路、电缆短路)与故障模式F_M5(过载)风险水平相同,故障模式F_M2(线路、电缆断路)与故障模式F_M9(程序丢失)风险水平相同,而现实中它们各自对数控系统的影响不同,究其原因是由于传统FMEA方法通过RPN值分析风险水平,虽然各故障模式3个影响因素O、S和D的等级数不同,但是相乘后可能造成RPN值相同即风险水平相同,本文通过TOPSIS中相对贴近度对各故障模式进行风险水平排序,有效地解决了此问题。
表 9 传统FMEA方法对各故障模式风险水平的分析Table 9 Analysis on risk level of failure mode using traditional FMEA method

故障模式	O	S	D	RPN
FM1	4	8	3	96
FM2	4	3	4	48
FM3	9	8	5	360
FM4	8	8	3	192
FM5	4	6	4	96
FM6	5	6	4	120
FM7	7	7	4	196
FM8	3	7	3	63
FM9	2	6	4	48

表选项


3 结 论本文在总结传统FMEA方法存在不足的基础上,提出了一种基于模糊TOPSIS的FMEA方法,并结合实例应用研究得出以下结论:
1) 采用模糊置信结构{(H_ij,α_ij^k(F_Mn,E_Fl))}(i>j;i=1,2，…,5;j=1,2，…,5;l=1,2,3;k=1,2,…，K；n=1,2,…,N)表达各故障模式影响因素的评价,并且评价人员根据自身知识经验给予不同的评价信息,从而将专家知识和经验引入FMEA过程,提高了分析的准确性。
2) 考虑研究对象的不同会引起各影响因素之间的相对重要性不同,将专家评价确定的各影响因素的权重和客观赋权法计算得到的权重相结合,综合分配各影响因素的权重,使得FMEA更加合理。
3) 根据TOPSIS的相对贴近度C_n对各故障模式的风险水平进行排序,避免了因出现相同的RPN值而导致不能判断风险水平高低的现象,也解决了传统FMEA通过影响因素相乘带来的问题。
4) 应用该FMEA方法对数控系统进行了分析,分析结果表明元器件损坏风险水平最高,对数控系统的危害性最大,在数控系统的设计、制造和使用中应重点关注,如:在数控系统的设计阶段,应注意元器件的选择、采购与验收;在数控系统使用阶段,应加强元器件的维护,做好相应的预防性维修措施,以提高数控系统的可靠性和可用性。
参考文献

[1]	陈颖,康锐.FMECA技术及其应用[M].2版.北京:国防工业出版社,2014:31-45. CHEN Y,KANG R.FMECA methodology and application[M].2nd ed.Beijing:National Defense Industry Press,2014:31-45(in Chinese).
[2]	陈政平,付桂翠,赵幼虎.改进的风险优先数(RPN)分析方法[J].北京航空航天大学学报,2011,37(11):1395-1399. CHEN Z P,FU G C,ZHAO Y H.Improved analysis method of risk priority number[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(11):1395-1399(in Chinese).
	Cited By in Cnki (16)
[3]	PILLAY A,WANG J.Modified failure mode and effects analysis using approximate reasoning[J].Reliability Engineering & System Safety,2003,79(1):69-85.
	Click to display the text
[4]	WANG Y M,CHIN K S,POON G K K,et al.Risk evaluation in failure mode and effects analysis using fuzzy weighted geometric mean[J].Expert Systems with Applications,2009,36(2):1195-1207.
	Click to display the text
[5]	GARGAMA H,CHATURVEDI S K.Criticality assessment models for failure mode effects and criticality analysis using fuzzy logic[J].IEEE Transactions on Reliability,2011,60(1):102-110.
	Click to display the text
[6]	CHIN K S,WANG Y M,POON G K K,et al.Failure mode and effects analysis using a group-based evidential reasoning approach[J].Computers & Operations Research,2009,36(6):1768-1779.
	Click to display the text
[7]	LIU H C,LIU L,BIAN Q H,et al.Failure mode and effects analysis using fuzzy evidential reasoning approach and grey theory[J].Expert Systems with Applications,2011,38(4):4403-4415.
	Click to display the text
[8]	GARCIA P A A,SCHIRRU R.A fuzzy data envelopment analysis approach for FMEA[J].Progress in Nuclear Energy,2005,46(3):359-373.
	Click to display the text
[9]	王贵宝,黄洪钟,张小玲.风险可能数——一种基于最大信息熵理论的风险度量和风险排序新方法[J].航空学报,2009,30(9):1683-1690. WANG G B,HUANG H Z,ZHANG X L.Risk possibility number-a new model for risk evaluation and prioritization based on maximum entropy theory[J].Acta Aeronautica et Astronautica Sinica,2009,30(9):1683-1690(in Chinese).
	Cited By in Cnki (20)
[10]	KUTLU A C,EKMEKÇIOĞLU M.Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J].Expert Systems with Applications,2012,39(1):61-67.
	Click to display the text
[11]	BRAGLIA M,FROSOLINI M,MONTANARI R.Fuzzy TOPSIS approach for failure mode,effects and criticality analysis[J].Quality and Reliability Engineering International,2003,19(5):425-443.
	Click to display the text
[12]	LIU H C,LIU L,LIN Q L.Fuzzy failure mode and effects analysis using fuzzy evidential reasoning and belief rule-based methodology[J].IEEE Transactions on Reliability,2013,62(1):23-36.
	Click to display the text
[13]	CHEN C B,KLEIN C M.A simple approach to ranking a group of aggregated fuzzy utilities[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,1997,27(1):26-35.
	Click to display the text
[14]	SONG W,MIN G X,WU Z,et al.Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS[J].International Journal of Computer Integrated Manufacturing,2013,26(12):1172-1186.
	Click to display the text
[15]	廖炎平,刘莉,龙腾.基于多属性决策的气动隐身多目标优化[J].机械工程学报,2013,48(13):132-140. LIAO Y P,LIU L,LONG T.Multi-objective aerodynamic and stealthy performance optimization based on multi-attribute decision making[J].Journal of Mechanical Engineering,2013,48(13):132-140(in Chinese).
	Cited By in Cnki (13)
[16]	王海巧,孙蓓蓓.基于实例推理的数控刀架快速设计方法[J].东南大学学报(自然科学版)2013,43(6):1232-1237. WANG H Q,SUN B B.Rapid design method of CNC turret based on case-based reasoning[J].Journal of Southeast University(Natural Science Edition),2013,43(6):1232-1237(in Chinese).
	Cited By in Cnki (2)
[17]	张海波,贾亚洲,周广文,等.数控系统故障模式、影响及危害度分析(FMECA)[J].中国机械工程,2004,15(6):491-494. ZHANG H B,JIA Y Z,ZHOU G W,et al.Failure mode,effects and criticality analysis(FMECA) of CNC system[J].Journal of Mechanical Engineering,2004,15(6):491-494(in Chinese).
	Cited By in Cnki (47)
[18]	战国璋.基于模糊理论的数控立式车床可靠性预计及故障分析技术[D].长春:吉林大学,2014:18-20. ZHAN G Z.Reliability prediction and fault analysis technology of CNC vertical lathe based on fuzzy theory[D].Changchun:Jilin University,2014:18-20(in Chinese).
	Cited By in Cnki (1)