然而,MMSE准则仅利用了误差信号的二阶统计量,因此基于MMSE准则的LMS自适应滤波器在非高斯环境中的收敛性能会变差,因此一些替代的优化准则被提出[10, 11]。最大相关熵准则(Maximum Correntropy Criterion,MCC)作为非高斯信号处理的最佳鲁棒准则,近年来已成功应用于自适应滤波领域[12, 13]。理论和实践均表明,基于MCC的自适应滤波器对非高斯噪声具有良好的鲁棒性。
本文在分数阶长LMS算法思想的基础上,提出一种用于MCC自适应滤波器的分数阶长(FT-MCC)算法。FT-MCC算法以MCC自适应滤波器最佳阶长的定义为出发点,利用不同阶长滤波器产生的相关熵之差实现阶长更新。MCC自适应滤波算法保证了滤波器对非高斯噪声具有较强的鲁棒性[13];分数阶长策略的应用扩展了MCC自适应滤波器的应用范围[6]。理论分析和实验结果表明,本文提出的FT-MCC算法在非高斯噪声情况下可有效提高自适应滤波器的收敛性能,优于现有的变阶长LMS算法。
1 MCC自适应滤波算法1.1 相关熵的特性分析相关熵作为2个随机序列和相似性的非线性度量,定义[12]为
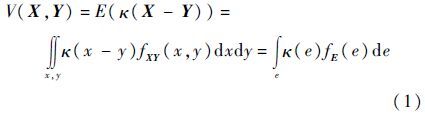
式中：E(·)为取期望操作；x、y为序列X、Y中对应位置的元素；fXY(x,y)为(X,Y)的联合概率密度函数；fE(e)为误差序列E=X－Y的分布函数；e=x－y为误差序列E中的元素；κ(·)为具有平移不变性的Mercer核函数，最常用的Mercer核函数为高斯核[13]：
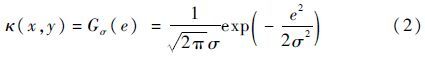
式中:σ>0为核宽度。
相关熵作为度量准则可应用于系统的指标评价[14]和系统的优化准则[15]中,2个序列间的相关熵越大,说明2个序列越相似。
在噪声滤波应用[15]中,当误差序列E呈现严重的非高斯分布,特别是呈现脉冲分布时,误差序列E中将会存在较大概率的大值偏差。这种情况下,由于高斯核中负指数项和核宽度σ的阈值作用,较大的偏差对相关熵的贡献将被削弱,不会出现偏差增大造成的数值不稳定情况,因此对非高斯环境下噪声滤波,相关熵准则具有较强的鲁棒性[15]。
1.2 MCC自适应滤波算法的鲁棒性分析MCC自适应滤波器的最优权向量通过最大化如下的代价函数进行求解:
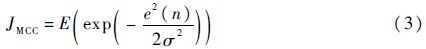
式中:n为迭代次数。
采用随机梯度法,可获得MCC自适应滤波算法(以下简称MCC算法)权向量的更新公式[12]:
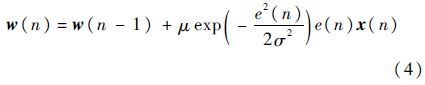
式中:w(n)为第n次迭代的滤波器权向量;x(n)为输入信号向量;μ>0为步长;e(n)=d(n)-w(n-1)Tx(n)为预测误差,d(n)为期望信号。
MCC算法的阶长为滤波器权向量w(n)的维数,同样也是输入信号向量x(n)的维数。当σ→∞,高斯核趋近于常数1,MCC算法退化为LMS算法[1]:
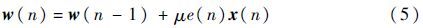
由式(4)和式(5)的对比可知:基于MMSE准则的LMS算法使得任何数值的预测误差e(n)都作用于滤波器权向量的更新,较大的预测误差易造成权向量的大幅波动;而MCC算法则削弱了数值较大的预测误差e(n)对滤波器权向量的贡献,使得权向量的更新一直是“平缓”的,这便是MCC改进自适应滤波器鲁棒性的原因。
2 MCC算法的分数阶长策略2.1 MCC算法的最佳阶长研究表明,随滤波器阶长的增加,LMS算法的稳态均方误差呈先减小后逐渐平稳的趋势[16];当阶长超过某一界限后,滤波器的稳态均方误差趋于平稳,过大的阶长并不能进一步改善滤波器的收敛性能,反而增加了其计算的复杂度。因此,LMS算法存在“最佳阶长”的概念,该“最佳阶长”使得LMS算法获得较低稳态均方误差的同时,也具有较低的计算复杂度[6]。
由式(3)可知,对于采用MCC算法的自适应滤波器而言,其收敛后的稳态相关熵与LMS算法得到的稳态均方误差呈现的变化趋势恰好相反:即随着阶长的增加,稳态相关熵先增加后逐渐平稳(极限为1)。
下面给出MCC算法最佳阶长的定义。
假设MCC算法当前的阶长为L,wL和xL为相应的滤波器权向量和输入向量,则其分割误差[6]为
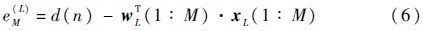
式中:wL(1∶M)和xL(1:M)分别为wL和xL前M个元素组成的向量,1≤M≤L。
与文献[6]中定义的分割稳态均方误差不同,本文定义MCC算法的分割稳态相关熵为
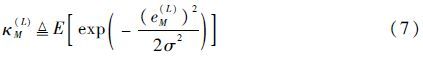
则MCC算法的最佳阶长Lopt应满足:
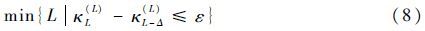
式中:Δ为正整数,满足:1≤Δ<L。
由式(2)可知,分割稳态相关熵κM(L)的性质与LMS算法分割稳态MMSE恰好相反,初始阶长L(0)较小的情况下,κL(L)≥κL-Δ(L),且随N的增大,κL(L)-κL-Δ(L)的值逐渐减小。当κL(L)-κL-Δ(L)的值小于某一预设值ε时,阶长达到最佳阶长值Lopt。
2.2 FT-MCC算法分数阶长策略首次提出“伪分数阶长”这一概念,解除了“更新阶长必须为整数”这一约束,同时将泄漏因子引入自适应过程中,较好地解决了梯度下降算法在阶长收敛过程中出现的“振荡”问题[6]。因此,基于分数阶长策略的FT-MCC算法可描述如下。
设lf为FT-MCC算法的“伪分数阶长”,则 “伪分数阶长”的更新公式为
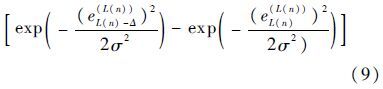
式中:α为泄漏因子;γ为“伪分数阶长”迭代计算用的步长因子。由于lf(n)不再被约束为整数,最终用于滤波器权向量更新的整数阶长L(n+1)通过如下判断获得:
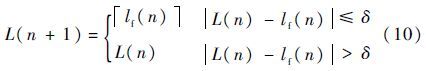
式中:δ为某一个预设的正数门限;$\left\lceil · \right\rceil $为向下取整操作。第n+1次迭代时,MCC算法权向量的更新公式(4)采用第n次迭代产生的阶长L(n+1),输入信号向量x(n)的维数也相应变为L(n+1)。
3 FT-MCC算法分析3.1 收敛性能分析对FT-MCC算法的收敛性能分析可从算法更新的平均意义上进行。对式(9)取期望,此时得到
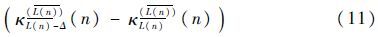
式中:$\overline{L(n)}$=E(L(n))为平均阶长;
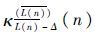和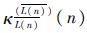
为式(7)定义的分割稳态相关熵。由于分割稳态熵随阶长的增大呈先递增后逐渐平稳的趋势,因此对于式(11)而言,如果L(0)选取的值较小,则$\overline{L(n)}$持续增大,直至
相反,如果L(0)选取的值较大,则$\overline{L(n)}$持续减小,直至
随着n的增大,$\overline{L(n)}$趋于稳定,此时式(11)和式(12)使得
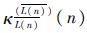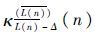-的稳定值在α/γ附近振荡。如果定义式(8)中的ε取值为α/γ,当n→∞时,$\overline{L(n)}$收敛的极限值就是最佳阶长Lopt。由式(8)可知,ε的取值应为一个比较小的值,因此在参数选取时应保证0<α$\ll $γ。值得注意的是,由于FT-MCC算法中设定了门限δ,因此$\overline{L(n)}$的稳定区间为(Lopt－δ,Lopt+δ)。当δ=1时,$\overline{L(n)}$的稳定区间为(Lopt－1,Lopt+1),取整后可知,$\overline{L(n)}$理论上可收敛于Lopt(参数δ并非关键参数,可取常值δ=1,在本文实验中不加以对比)。FT-MCC算法采用了具有非线性特性的高斯核函数,这导致对FT-MCC算法进行二阶稳态分析远比分数阶长LMS算法要困难。然而,由于同属于分数阶长策略,FT-MCC算法涉及的参数Δ、α、γ和δ的选取原则可参考分数阶长LMS算法各参数的选取原则[17](详见第4节实验部分);对FT-MCC算法稳态阶长L(∞)的估计也可参考分数阶长LMS算法稳态阶长的范围[17]:
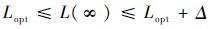
3.2 计算复杂度分析下面对比分析FT-MCC算法和分数阶长LMS算法的计算复杂度,分析过程只计每次权向量迭代更新过程的乘法操作数。
假设当前的阶长为L,对比式(4)和式(5)可知,LMS算法单次迭代需要2L+1次乘法[18],MCC算法需要2L+4次乘法(指数项可采用查找表的方式实现)。因此对于阶长为L和L-Δ的2种滤波器而言,分数阶长LMS算法在权向量更新时需要4L-2Δ+2次乘法,FT-MCC算法需要4L-2Δ+8次乘法。在“伪分数阶长”的更新过程中,分数阶长LMS算法需要3次乘法[6],FT-MCC算法仅需要1次乘法(指数项已在式(4)中计算)。
因此,分数阶长LMS算法的计算复杂度为4L-2Δ+5,FT-MCC算法的计算复杂度为4L-2Δ+9,二者相近。
3.3 鲁棒性分析FT-MCC算法的鲁棒性主要是指算法在非高斯环境下阶长收敛的稳定性。在非高斯噪声环境中,不论滤波器处于瞬态阶段还是稳态阶段,强功率的噪声信号都会使得滤波器输出偏差较大的预测误差。由式(9)可知,随着预测误差的增大，2个指数项的数值会减小,这样便有效抑制了大值预测误差对阶长更新的影响。另外,适当地选择泄漏因子α和步长因子γ(本文实验中将加以验证),也会保证FT-MCC算法在单次迭代中获得的分数阶长不会出现大幅度变化。因此,即使在较严重非高斯环境中,FT-MCC算法也可使自适应滤波器的阶长收敛具有强的鲁棒性。
4 实验结果与分析本节利用非高斯噪声环境下的系统辨识实验对FT-MCC算法的性能进行验证。图 1为系统辨识问题的示意图。图中：u(n)为第n次采样的输入信号,分别输入到自适应滤波器和未知系统(设未知系统的权向量为w0)；y(n)为自适应滤波器的输出；s(n)为未知系统的输出；v(n)为观测噪声;d(n)=w0Tx(n)+v(n)为自适应滤波器的期望信号,x(n)=(u(n),u(n-1),…,u(n-L+1))为输入信号序列。
 |
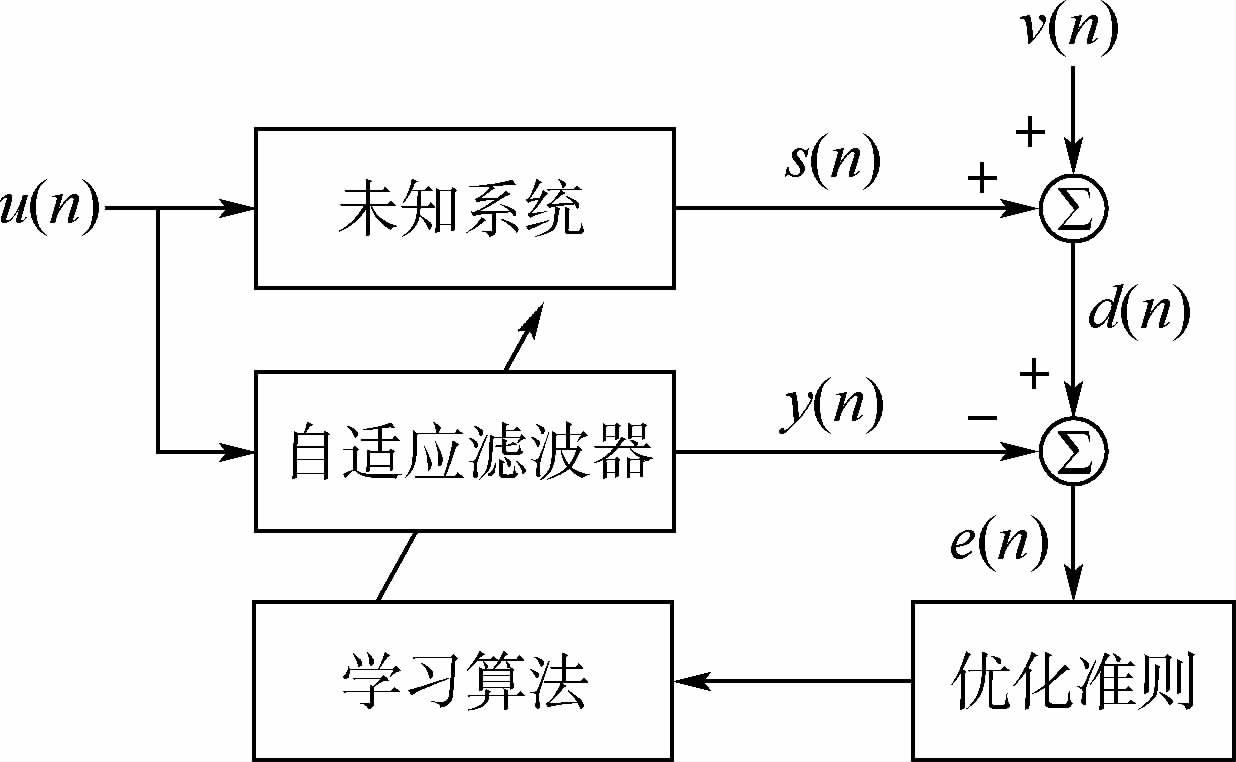| 图 1 系统辨识问题示意图Fig. 1 Schematic of system identification application |
| 图选项 |
在相应优化准则下,学习算法利用误差信号e(n)=d(n)-y(n)对自适应滤波器权向量进行更新,完成对未知系统的“辨识”,即利用自适应滤波器完成对未知系统的重新建模。但由于系统是未知的,如果对系统的阶数估计不准确可能会噪声对系统的“过建模”(估计阶数高于实际阶数)和“欠建模”(估计阶数低于实际阶数),适当偏差的“过建模”和“欠建模”是可以接收的[6]。本实验中的优化准则为MCC,学习算法为FT-MCC算法。输入信号u(n)采用均值为0、方差为1的高斯白噪声序列,序列长度为15000。
实验1 验证FT-MCC算法中各参数对算法性能的影响。
未知系统选择为11阶的无线信道模型,其冲击响应系数为[0.6964 0.6207 0 0.247 10.2202 0 0 0.1238 0 0 0.0696]。观测噪声选择为描述非高斯脉冲噪声的有效模型:对称α-稳定噪声模型噪声[19],其分布函数为
式中:α为特征指数;β为散度。实验中选取α=1.5,β=0.1。图 2为实验中的对称α-稳定噪声幅值。
 |
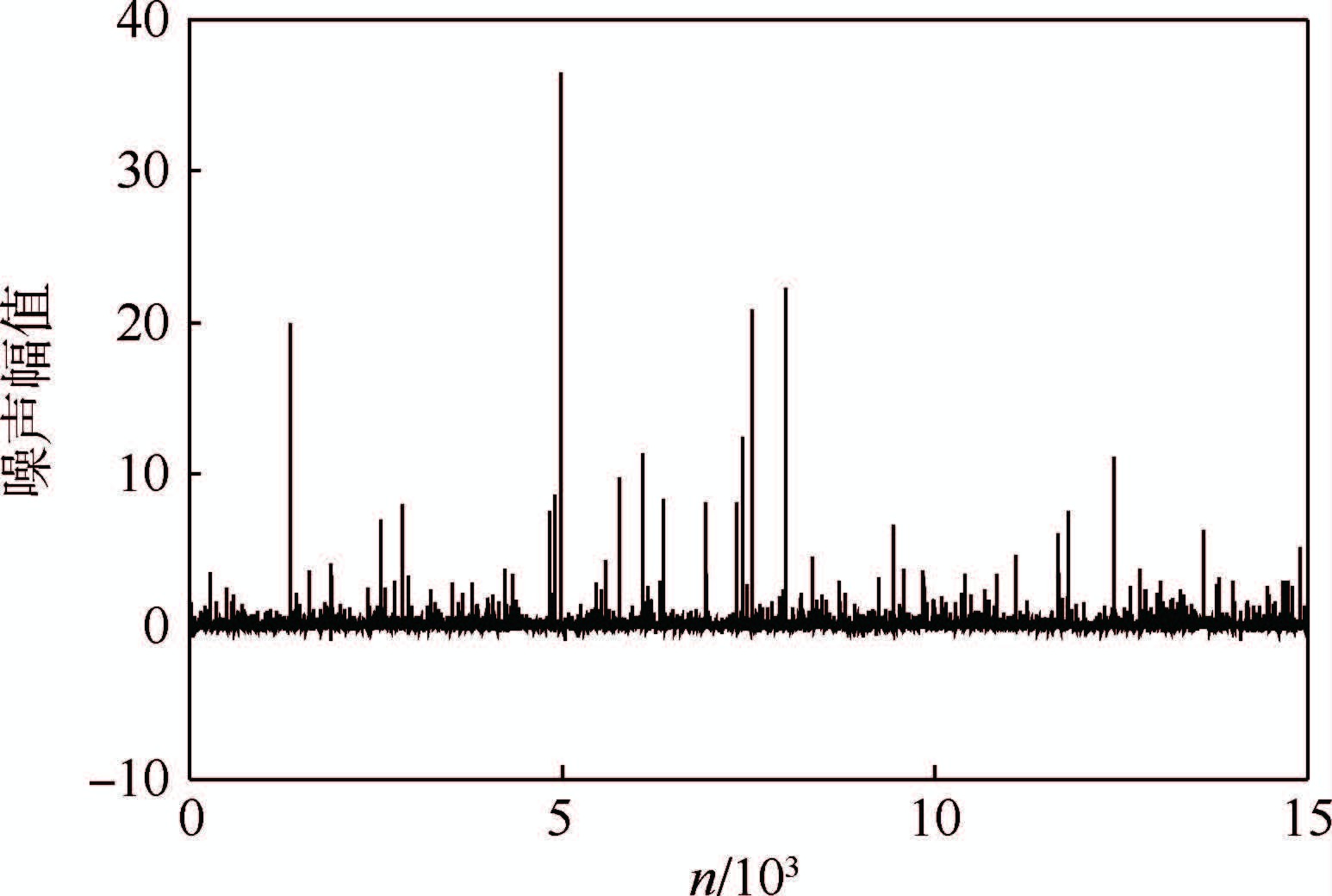| 图 2 对称α-稳定噪声模型分布Fig. 2 Distribution of symmetric α-stable noise |
| 图选项 |
在研究FT-MCC算法的性能之前，首先研究MCC算法阶长L与稳态相关熵κE之间关系。实验中的稳态相关熵κE可以采用以下关系近似：
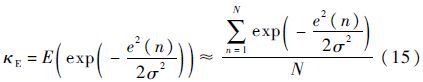
稳态相关熵κE能较好地反应出MCC算法的收敛性能,κE的值越接近1,代价函数式(3)的求解越准确,算法的稳态性能越好。实验中选取阶长L的范围为1～20,图 3为稳态相关熵随阶长变化的关系。
 |
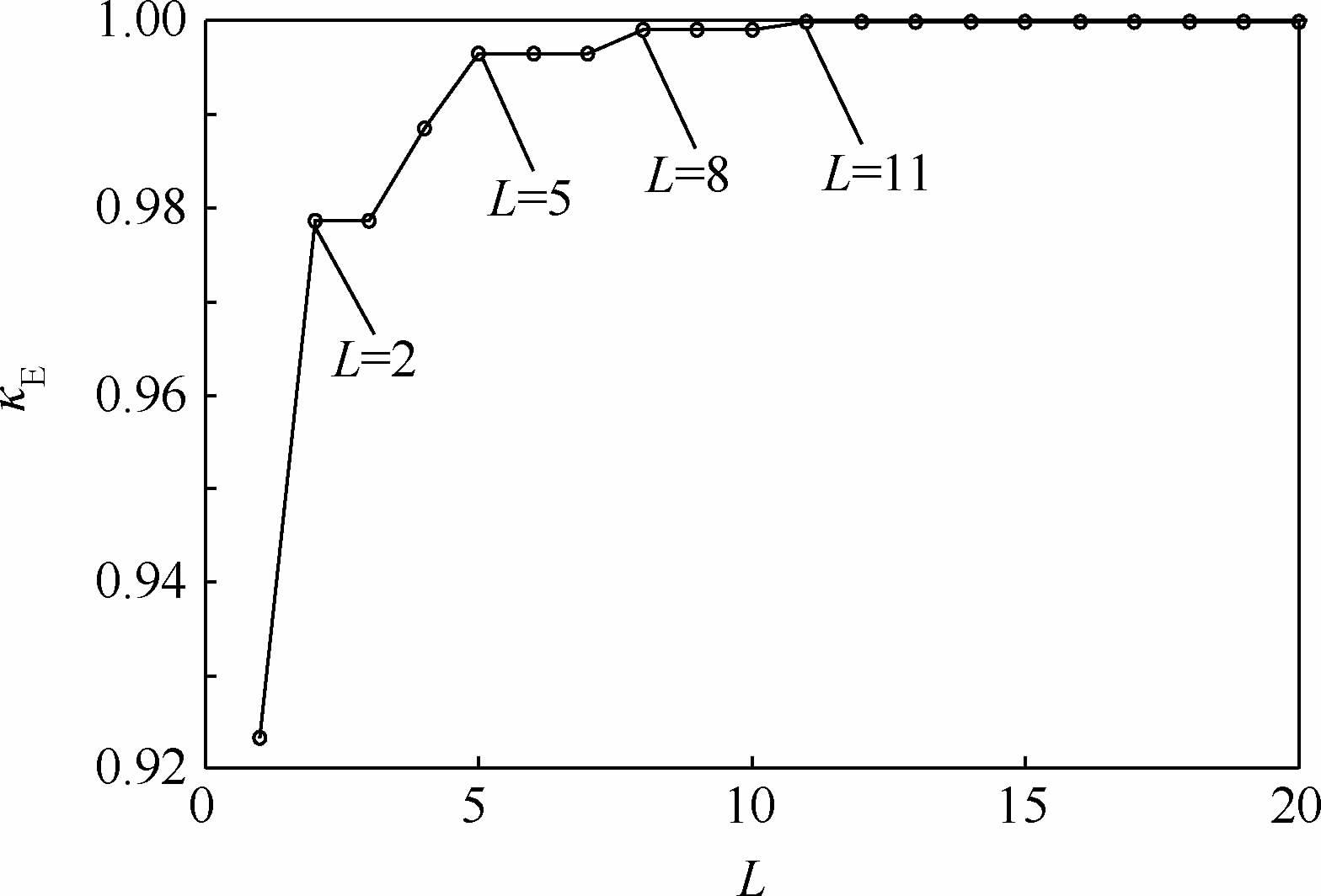| 图 3 稳态相关熵随阶长变化的关系Fig. 3 Relationship between steady-state correntropy and tap-lengths |
| 图选项 |
如图 3所示,稳态相关熵随阶长的增大符合先递增后平稳的趋势,阶长从11以后趋于平稳,因此可以认为自适应滤波器的“最佳阶长”为11。值得注意的是,稳态相关熵随阶长变化的关系函数中存在3个局部最优解L=2,L=5和L=8,如果算法参数选择不当,FT-MCC算法容易陷入局部最优解,这一点将在以下实验中加以验证。
实验中对比4组FT-MCC算法(δ=1)的参数设置如下:
算法1 Δ=3,α=0.001,γ=20。
算法2 Δ=2,α=0.001,γ=20。
算法3 Δ=3,α=0.01,γ=20。
算法4 Δ=3,α=0.001,γ=80。
算法5 Δ=3,α=0.01,γ=80。
3组算法权向量更新步长均取μ=0.01,初始阶长L(0)均取5。图 4为算法1~5的阶长变化曲线对比。
 |
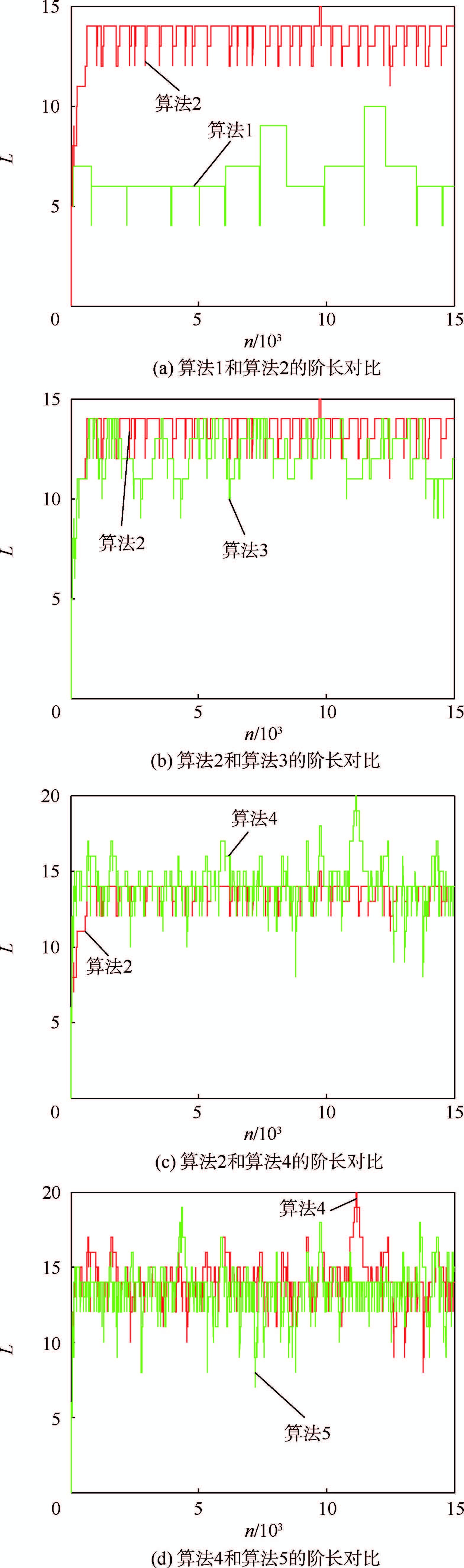| 图 4 算法1～5的阶长变化对比Fig. 4Tap-length comparisons of algorithm 1-5 |
| 图选项 |
图 4(a)中,算法1能较好地跟踪未知静态系统的阶长,稳定后的阶长在12～15之间变化,常态值为15,符合对FT-MCC算法稳态阶长L(∞)的估计,而算法2由于参数Δ选择偏小,在迭代更新中没能完全跳出L=5和L=8这2个局部最优解,因而出现“欠建模”现象;图 4(b)中,算法3由于泄露因子α选择偏大,导致算法收敛较慢,且α/γ偏大导致稳态阶长较算法1有较大波动;图 4(c)中,算法4由于步长因子γ选择偏大,算法虽然可以较快地收敛,但较大的迭代步长导致稳态阶长波动剧烈;图 4(d)中,算法5较算法4加大了泄露因子α,但这样并未改善收敛性能,反而大的泄露因子使α/γ值较大,因而导致稳态阶长波动剧烈。
由算法1～5的对比可知,在FT-MCC算法中,步长因子γ为最重要的参数,过大的γ虽然可以提高算法的收敛速度,但也会导致算法的稳态阶长浮动偏大;泄露因子α的选择也很重要,过大的α会导致 “伪分数阶长” 单次迭代的泄漏值过大,阶长收敛速度变慢,同时偏大的α/γ比值也导致稳态阶长的波动较大;Δ的取值不宜过小,否则会使算法陷入局部最优解,而前面的分析可知,其值也不宜过大,否则会导致稳态阶长L(∞)的浮动范围过大。
实验2 验证FT-MCC算法与3种不同变阶长LMS算法：分割滤波(SF-LMS)算法[4]、梯度下降(GD-LMS)算法[5]和分数阶长(FT-LMS)算法的性能对比。
辨识实验中采用未知突变系统,突变系统权向量w0构造为如下2个系统的组合:
当n<5000或n>10000时,w0=w1;当5000≤n≤10000时,w0=w2。ak和bk由均值为0、方差为1的高斯噪声序列产生。本次实验中观测噪声v(n)建模为另一种典型的非高斯分布模型——混合高斯模型噪声,其分布函数为
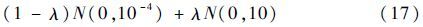
图 5为λ=0.05时混合高斯模型噪声的分布函数。
 |
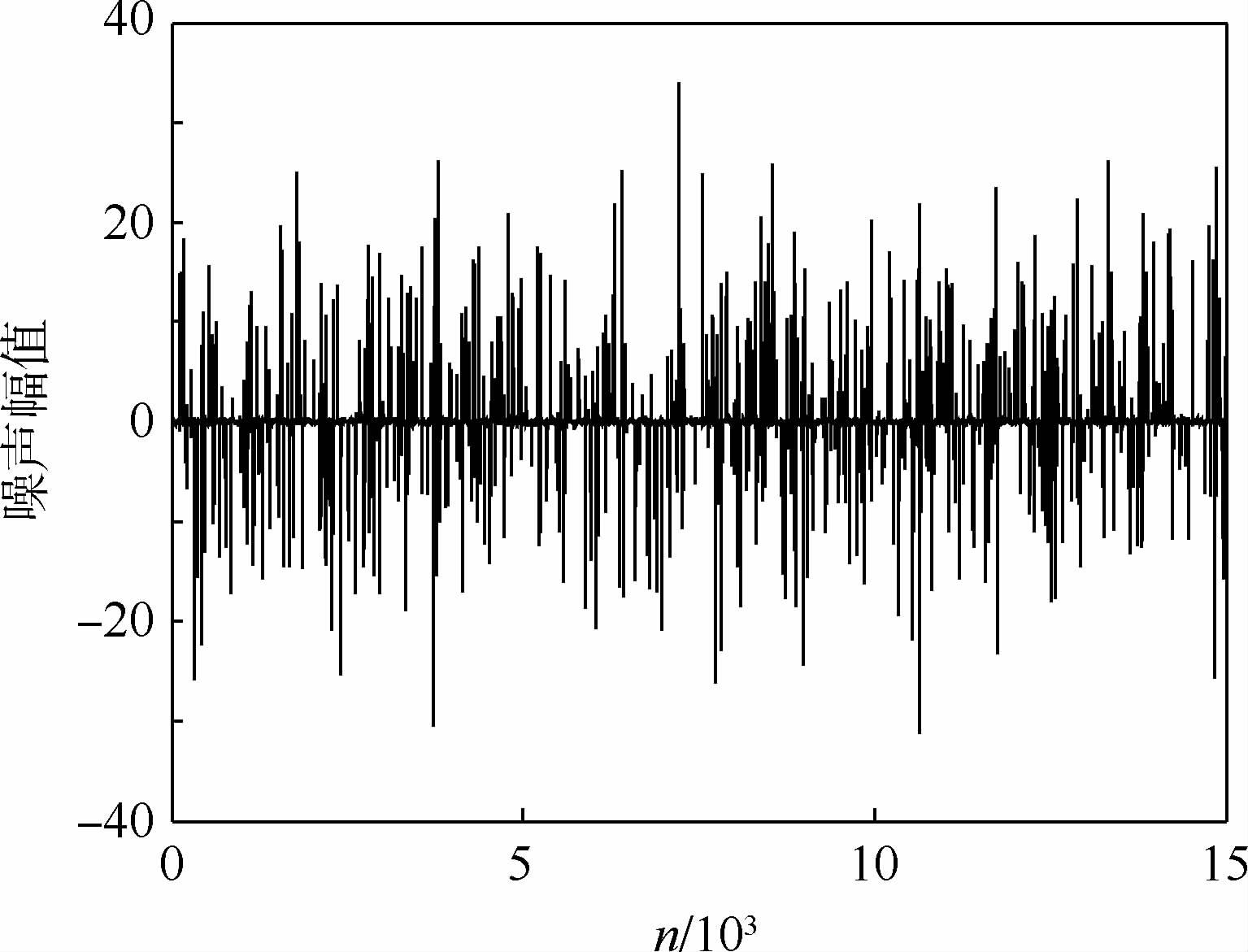| 图 5 混合高斯模型噪声Fig. 5 Gaussian-mixture model noise |
| 图选项 |
如图 5所示,混合高斯模型噪声呈现出低功率高斯背景噪声和高功率脉冲噪声的混合特性。表 1为实验中4种算法的参数设置。
表 1 4种算法的参数设置Table 1 Parameter setting for four algorithms
| 参数设置 | SF-LMS | GD-LMS | FT-LMS | FT-MCC |
| Δ | 10 | 10 | 10 | 10 |
| α | 1 | 0.001 | 0.001 | 0.001 |
| β | 0.99 | |||
| γ | 30 | 30 | ||
| δ | 1 | 1 | 1 | 1 |
表选项
以上4种算法权向量更新步长均取μ=0.01,初始阶长均取L(0)=30。图 6为上述4组算法的阶长变化曲线。
 |
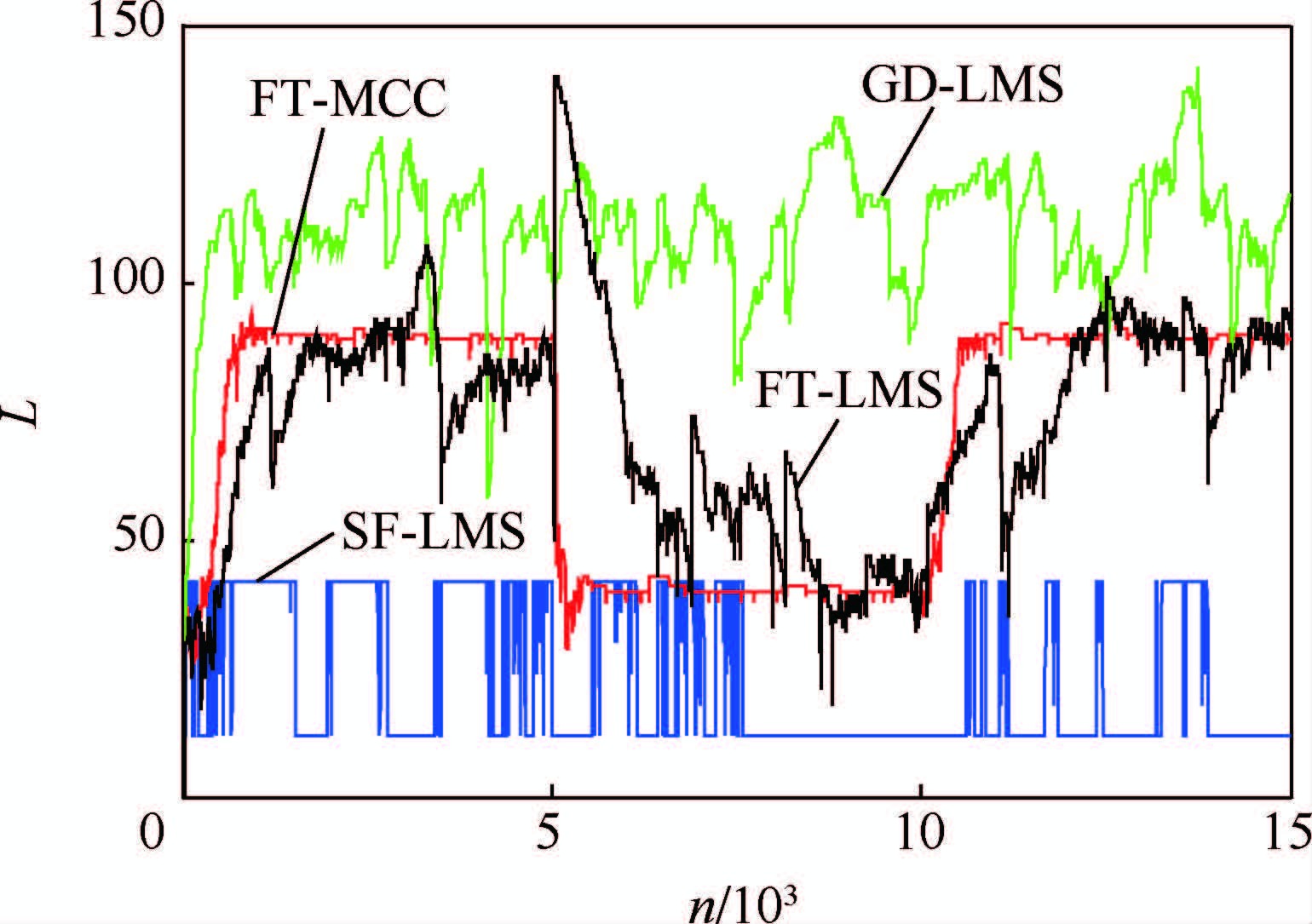| 图 64组算法的阶长变化曲线Fig. 6 Tap-length evolution curves of four groups of different algorithm |
| 图选项 |
如图 6所示,FT-MCC算法选用较小的α和适中的γ,阶长变化曲线能较好地跟踪未知系统的阶长变化,稳态阶长处在Lopt≤L(∞)≤Lopt+Δ的范围内;SF-LMS算法由于采用整数的阶长变化,阶长曲线呈“方波”形式变化,脉冲噪声导致阶长无法收敛;GD-LMS算法虽然也采用整数阶长,但噪声导致梯度信息变化不稳定,使得阶长浮动较大,算法无法收敛;FT-LMS算法在整个迭代过程中有跟踪目标系统变化的趋势,但脉冲噪声使得阶长始终不能稳定收敛,尤其是系统突变的时刻阶长浮动较大。
由实验2的结果可知,相比现有的3种变阶长LMS算法,FT-MCC算法可以有效抑制非高斯噪声的干扰。
实验3 验证噪声的非高斯程度对FT-MCC算法收敛性能的影响。
对于式(17)的混合高斯模型,λ越大表示高功率随机脉冲信号所占的比例越大,信号的非高斯性也越强。实验中选取4组λ值:0、0.1、0.2和0.5,FT-MCC算法的参数设置同实验2。图 7为4组λ值对应的阶长变化曲线。
 |
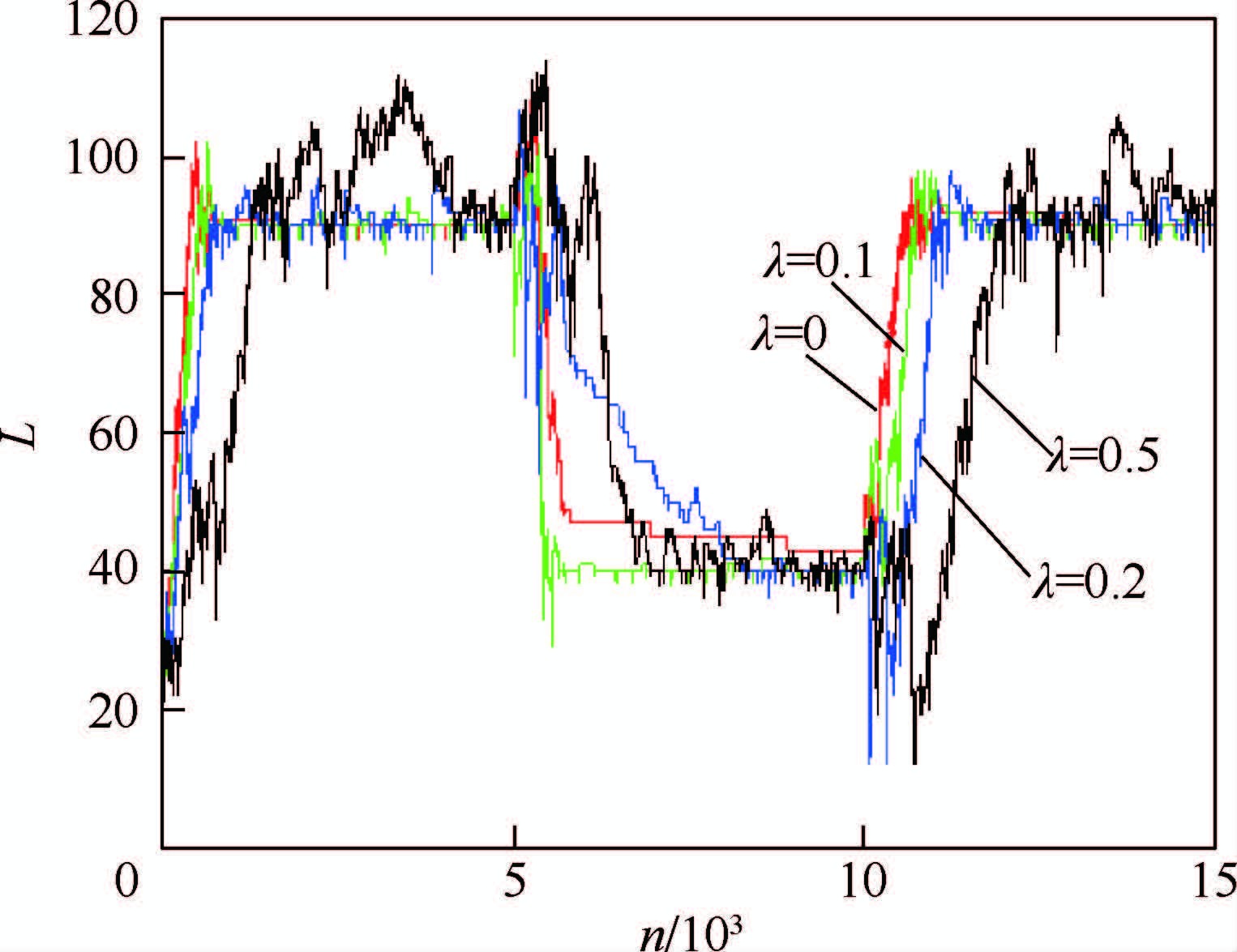| 图 7 4组λ值对应的阶长变化曲线Fig. 7 Tap-length evolution curves according to four groups of different λ |
| 图选项 |
如图 7所示,当λ=0时,系统处于高斯噪声环境中,FT-MCC算法的阶长在整个迭代过程中均能够较好地收敛;当λ=0.1时,环境中增加的脉冲信号致使系统在发生突变时阶长变化出现轻微的波动,但算法仍能够较好地收敛;当λ=0.2时,环境噪声的非高斯特性进一步加强,系统突变时阶长出现较剧烈的波动,算法收敛速度减缓;当λ=0.5时,环境中的高功率脉冲噪声已经占到50%,此时无论是在稳态阶段还是突变时刻,阶长均出现较剧烈的波动,算法收敛性变差。因此,随着环境噪声非高斯性的逐渐增强,FT-MCC算法稳态阶长的收敛性逐渐变差。
5 结 论本文基于分数阶长的变阶长策略,提出了一种分数阶长MCC算法——FT-MCC算法,通过实验验证表明:
1) 在非高斯噪声环境中,FT-MCC算法可使自适应滤波器具有较强的鲁棒性,算法各参数的选取规则遵循分数阶长LMS算法的参数选取规则。
2) 相比现有的变阶长LMS算法,FT-MCC算法在非高斯噪声严重,特别是存在大功率脉冲干扰的情况下可实现对最佳阶长稳定的跟踪和估计。
3) FT-MCC算法抑制非高斯噪声的能力并非无限,随着噪声非高斯性的增强,算法稳态阶长的收敛性相应变差。
本文提出的FT-MCC算法可扩展到非高斯噪声环境下变阶长自适应滤波器的其他应用领域。为了进一步提高算法的收敛性能,算法的可变参数策略[7, 8, 9]将是值得继续研究的方向。另外,对FT-MCC算法做进一步的稳态性能分析也是下一步需要做的工作。
参考文献
| [1] | TAN Y,HE Z Q,TIAN B Y.A novel generalization of modified LMS algorithm to fractional order[J].IEEE Signal Processing Letters,2015,22(9):1244-1248. |
| Click to display the text | |
| [2] | SCHOBER R,GERSTACKER W H,LAMPE A.Non-coherent MMSE interference suppression for DS-CDMA[J].IEEE Transactions on Communications,2002,50(4):577-587. |
| Click to display the text | |
| [3] | SLOCK D T M.On the convergence behavior of the LMS and the normalized LMS algorithms[J].IEEE Transactions on Signal Processing,1993,41(9):2811-2825. |
| Click to display the text | |
| [4] | RIERA-PALOU F,NORAS J M,CRUICKSHANK D G M.Linear equalizers with dynamic and automatic length selection[J].Electronics Letters,2001,37(25):1553-1554. |
| Click to display the text | |
| [5] | GU Y T,TANG K,CUI H J.LMS algorithm with gradient descent filter length[J].IEEE Signal Processing Letters,2004,11(3):305-307. |
| Click to display the text | |
| [6] | GONG Y,COWAN C F N.An LMS style variable tap-length algorithm for structure adaptation[J].IEEE Transactions on Signal Processing,2005,53(7):2400-2407. |
| Click to display the text | |
| [7] | LI L L,CHAMBERS J A.A novel adaptive leakage factor scheme for enhancement of a variable tap-length learning algorithm[C]//IEEE International Conference on Acoustics,Speech and Signal Processing.Piscataway,NJ:IEEE Press,2008:3837-3840. |
| Click to display the text | |
| [8] | XU D J,YIN B,WANG W,et al.Variable tap-length LMS algorithm based on adaptive parameters for TDL structure adaption[J].IEEE Signal Processing Letters,2014,21(7):809-813. |
| Click to display the text | |
| [9] | LIU Z Y.Variable tap-length linear equaliser with variable tap-length adaptation step-size[J].Electronics Letters,2014,50(8):587-589. |
| Click to display the text | |
| [10] | ERDOGMUS D,PRINCIPE J C.Generalized information potential criterion for adaptive system training[J].IEEE Transactions on Neural Networks,2002,13(5):1035-1044. |
| Click to display the text | |
| [11] | SINGH A,PRINCIPE J C.Using correntropy as a cost function in linear adaptive filters[C]//International Joint Conference on Neural Networks.Piscataway,NJ:IEEE Press,2009:2950-2955. |
| Click to display the text | |
| [12] | LIU W,POKHAREL P P,PRINCIPE J C.Correntropy:Properties and applications in non-Gaussian signal processing[J].IEEE Transactions on Signal Processing,2007,55(11):5286-5298. |
| Click to display the text | |
| [13] | CHEN B,LEI X,LIANG J,et al.Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion[J].IEEE Signal Processing Letters,2014,21(7):880-884. |
| Click to display the text | |
| [14] | HE R,ZHENG W S,HU B G.Maximum correntropy criterion for robust face recognition[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2011,33(8):1561-1576. |
| Click to display the text | |
| [15] | ZHAO S,CHEN B,PRINCIPE J C.Kernel adaptive filtering with maximum correntropy criterion[C]//Proceedings of International Joint Conference on Neural Networks.Piscataway,NJ:IEEE Press,2011:2012-2017. |
| Click to display the text | |
| [16] | WEI X H,CRUICKSHANK D G M,MULGREW B,et al.A unified approach to dynamic length algorithms for adaptive linear equalizers[J].IEEE Transactions on Signal Processing,2007,55(3):908-920. |
| Click to display the text | |
| [17] | ZHANG Y,LI N,CHAMBER J A,et al.Steady-state performance analysis of a variable tap-length LMS algorithm[J].IEEE Transactions on Signal Processing,2008,56(2):839-845. |
| Click to display the text | |
| [18] | HAYKIN S.Adaptive filter theory[M].4th ed.Englewood Cliffs,NJ:Prentice Hall Press,1996:276-277. |
| [19] | 刘明骞,李兵兵,曹超凤.非高斯噪声下数字调制信号识别方法[J].电子与信息学报,2013,35(1):85-91. LIU M Q,LI B B,CAO C F.Recognition method of digital modulation signals in non Gaussian noise[J].Journal of Electronics & Information Technology,2013,35(1):85-91(in Chinese). |
| Cited By in Cnki (14) |
