目前,CS算法已在结构优化问题[3]、六杆停歇机构运动轨迹优化[4]、可靠性冗余分配[5]和机构运动精度可靠性分析[6]等领域得到了广泛的应用,而在对CS算法的改进方面,主要涉及对算法中控制参数的自适应处理、与其他优化算法的混合或逐维改进解的质量等方面。例如,Zhang等[7]将鸟窝更新做了并行处理,以增加解的多样性,并对搜索步长做了自适应改进以加强局部搜索能力;Walton等[8]对适应性好的鸟窝与被抛弃的鸟窝做了不同搜索步长的处理,并在产生新解时加入了各鸟窝之间的信息交流,该改进算法在收敛性上要优于DE算法、PSO算法和CS算法;Kanagaraj等[5]将遗传算法(GA)与CS算法融合,提高了CS算法在开发和探索能力之间的平衡性,Valian等[9]对Lévy flights步长和外来鸟蛋被发现概率引入了自适应机制,以上2种CS算法的改进形式都用在了系统可靠性冗余分配问题中,实验结果表明改进后的CS算法的寻优能力均要优于标准CS算法;王李进等[10]在CS算法中引入逐维改进的策略并改变了鸟窝飞行步长的更新方式,以增强算法的开发能力,该改进算法在求解多维函数优化问题上具有一定的优势。虽然文献[6, 7, 8, 9]都对CS算法中的飞行步长做了自适应改变,且取得了较好的寻优效果,但是并没有一个确定的数学模型可供选择。另外,CS算法中的鸟窝位置更新公式仅对被淘汰的鸟窝进行更新,而被保留下来的鸟窝不做任何改变,这就在一定程度上限制了该算法的开发能力。
为了克服上述CS算法存在的问题,增强CS算法的开发能力,提高收敛速度和计算精度,本文提出全局最优导向模糊布谷鸟搜索(FGCS)算法。首先,在CS算法中的鸟窝更新公式中引入全局最优导向策略,对保留下来的具有较好适应性的鸟窝朝向当前最优鸟窝位置迭代更新,不仅能够保证计算过程中鸟窝的多样性,而且提高了算法的开发能力和收敛速度;其次,采用模糊逻辑规则对CS算法中的外来鸟蛋被发现概率和Lévy flights步长进行动态调整,解决了CS算法计算精度较差的问题,且更好地权衡了CS算法的探索能力和开发能力;最后,将所提出的算法应用于结构机构可靠性分析中,并与其他优化算法进行对比分析,通过算例进一步验证了所提算法的可行性与优越性。
1 CS算法布谷鸟是利用寄宿产蛋的方式进行繁殖的特殊鸟类。Yang和Deb[1, 2]首先假设每只布谷鸟随机地选取其他鸟类的巢穴进行产蛋,且每次只产一个鸟蛋,每个鸟蛋相当于一个解向量,在每次迭代计算中,具有最优适应性的鸟蛋将被保留至下一次的迭代过程,而在所有寄宿的鸟窝中,布谷鸟鸟蛋被宿主发现的概率为[0,1]之间的数值,以pa表示。当宿主发现自己的鸟窝有外来鸟蛋时,它们会抛弃该外来鸟蛋或在它处另建新巢,以保证每次迭代过程中鸟窝数量的一致。Yang和Deb根据上述布谷鸟的繁殖方式以及Lévy flights随机行走方式抽象出了CS算法[1]。在CS算法中,布谷鸟是根据以下公式对鸟窝位置进行更新的:
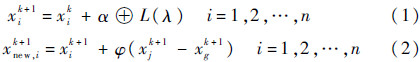
式(1)为布谷鸟根据Lévy flights进行随机寻巢;式(2)为宿主根据外来鸟蛋被发现概率pa进行选择抛弃,并建立新的鸟窝。其中:xik与xik+1分别为第i个鸟蛋在第k代和第k+1代所处的鸟窝位置;⊕为点乘积;α=α0(xik-xkbest)为Lévy flights随机行走中的步长控制量,α0为常数,xkbest为当前最优解,α用来保证在第k代中的最优解附近得到第k+1代的解,以提高算法的局部搜索能力[1];L(λ) 为Lévy flights随机搜索路径;φ为缩放因子,是服从均匀分布的[0,1]区间内的随机数;xjk+1与xgk+1为通过式(1)得到的第k+1代中的2个随机解。经过Lévy flights随机行走和选择重建鸟巢的步骤之后,完成了一次迭代操作,得到了新一代的鸟窝位置,记为xk+1new,i。
2 FGCS算法2.1 全局最优导向鸟窝位置更新公式由式(1)可知,CS算法在寻优过程中利用Lévy flighes,使得该算法具有很强的探索能力,但在用式(2)计算新解的过程中,是通过任意选择当前的鸟窝进行淘汰更新,这就不能保证得到的新解的质量一定比当前解的质量要好,从而导致收敛速度较慢。另外,在式(2)中,只有被抛弃的鸟窝进行了随机行走并建立了新的鸟窝,而被保留的鸟窝仍然停留在原处,这样不利于种群的多样性,且在每一次迭代进行最后的鸟窝适应值评估时,还要将保留下来的鸟窝进行比对,导致算法的效率降低。所以CS算法有着较强的探索能力,但开发能力相对较弱。受粒子群算法以及文献[11]的启发,本文利用具有全局最优导向性质的鸟窝更新公式替代式(2),以提高CS算法的开发能力并提升收敛速度,这里称为全局最优导向布谷鸟搜索(Global-best guided Cuckoo Search,GCS)公式:
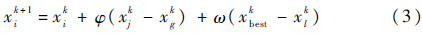
式(3)是基于最优策略的搜索方程,比式(2)增加了等式右边的第3项,称为全局最优鸟窝引导搜索项。在生成新解时,式(3)用到了当前解中的最优信息。其中:xlk为不同于xjk和xgk的随机解;ω为黄金比例系数ρ与偏移量δ的乘积,即
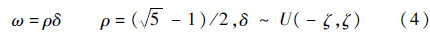
在式(4)中,δ是服从(-ζ,ζ)区间均匀分布的随机数,在计算过程中取ζ=π/6[12]。由式(3)和式(4)可知,在全局搜索项中是根据黄金分割比例朝向全局最优解产生新解,由黄金比例系数所产生的新解要明显优于在[0,1]区间产生随机数而得到的新解[8],但是新解并不在xkbest与xlk之间线性产生,而是偏移一个角度δ,这样能够使得CS算法能够在搜索空间中得到更多的位置信息。
2.2 CS算法中参数的模糊调整策略布谷鸟鸟蛋被宿主发现的概率pa和Lévy flights中的飞行步长控制量α0是标准CS算法的2个可控也是最为重要的参数。为了提高标准CS算法的寻优性能,文献[9]所提出的改进布谷鸟搜索(ICS)算法对pa和α0做出了随着迭代次数呈线性或非线性改变的调整策略,且取得了不错的效果。但是在如何调整这2个参数而能最好地权衡该算法的开发能力和探索能力上,并没有确切的数学模型可选择,此时,模糊逻辑系统为动态调整α0与pa这2个参数提供了一个很好的方法[13, 14]。
为了使得CS算法在迭代计算的前期有较好的探索能力而最终有较强的开发能力,本文设计一个具有模糊逻辑规则控制CS算法参数的FGCS算法。以鸟窝位置之间的分散性和迭代次数作为模糊系统的输入变量,将pa与α0作为输出变量。其中,模糊系统的输入变量鸟窝之间的分散性为
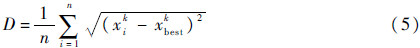
式(5)表示在每次循环迭代结束后,各个鸟窝位置与最优鸟窝位置之间的欧式距离,能够度量鸟窝之间的分散程度。为了便于计算,本文对迭代次数与分散性这2个模糊系统的输入变量进行模糊化处理,将其值均转化到[0, 1]区间。如式(6)和式(7)所示:

式中:KNorm和DNorm为将当前迭代次数k与分散性D进行标准正态化后的模糊系统输入参数;Kmax为最大迭代次数;Dmin和Dmax分别为每次迭代中分散性的最小值和最大值。
可以看出,FGCS算法与ICS算法是通过不同的策略对CS算法中的参数进行调整。其中,ICS算法分别通过线性和非线性方程对pa和α0进行了与迭代次数相关的自适应改变,而FGCS算法是通过模糊逻辑规则对pa和α0进行调整,与ICS算法相比,仅增加了一个控制参数,即鸟窝之间的欧氏距离作为模糊系统的输入变量。另外,FGCS算法对CS算法中的鸟窝更新公式增加了全局最优导向项,这会提高算法的收敛效率,并不增加算法的复杂性。
在标准CS算法中,取pa=0.25,α0=0.01[2]。在本文所设计的模糊系统中,将pa和α0的取值扩大至其上述推荐值的附近范围内:pa∈[0.1,0.5],α0∈[0.005,0.020]。在该模糊系统中,2个模糊输入变量KNorm和DNorm与2个模糊输出变量pa和α0分别由3个三角形隶属度函数和5个三角形隶属度函数确定,即将模糊输入的范围平均分成3个模糊集,输出的范围平均分成5个模糊集,分别如图 1和图 2所示。图中:L表示低;M表示中;H表示高;ML表示中低;MH表示中高。
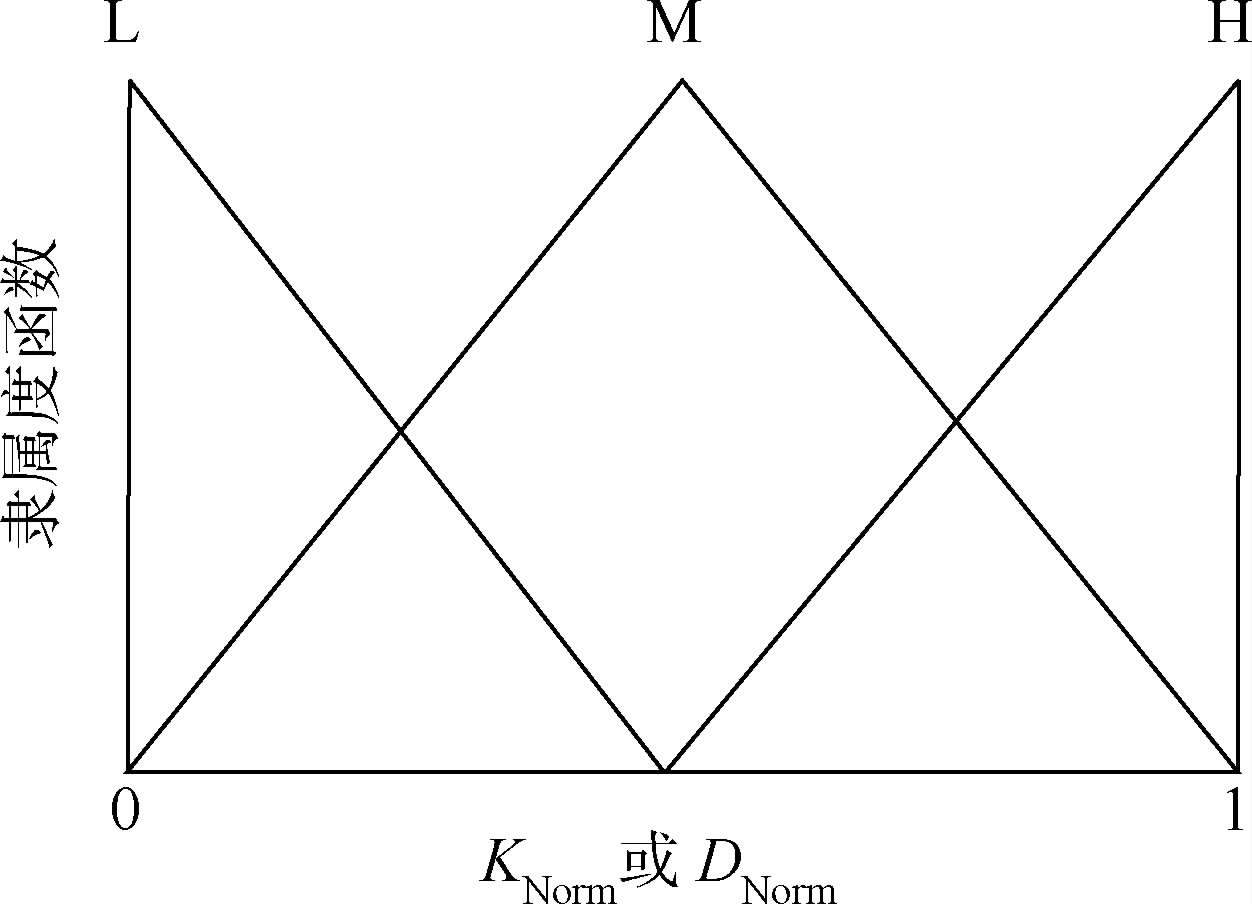 |
| 图 1 输入变量KNorm和DNormFig. 1 Input variables KNormand DNorm |
| 图选项 |
 |
| 图 2 输出变量pa和α0Fig. 2 Output variables pa and α0 |
| 图选项 |
了解pa和α0如何影响该算法的计算性能有助于该模糊系统逻辑规则的制定。pa表示在一组固定的鸟窝数量中,每次迭代会以pa的概率淘汰一部分鸟窝,然后另建与淘汰的鸟窝数量相同的新窝,其余的鸟窝则会被保留,该参数影响着鸟窝的更新速度。而α0控制步长的大小,在迭代计算早期,为保证算法的全局寻优,应将较多的鸟窝淘汰掉而建立新的鸟窝,以获得搜索空间中更多的位置信息,且Lévy flights步长应较大,以探索更多的区域,所以pa与α0应为较大值。随着寻优计算的进行,α0与pa应逐渐减小,使算法在全局最优解附近进行寻优以得到高精度的解[6]。根据上述参数调整思想,系统的模糊逻辑规则如表 1所示。
表 1 模糊逻辑规则Table 1 Fuzzy logic rules
| 变量 | K Norm | |||
| L | M | H | ||
| p a, α 0 | p a, α 0 | p a, α 0 | ||
| D Norm | L | H,H | MH,H | ML,ML |
| M | MH,MH | M,M | ML,L | |
| H | MH,M | M,ML | L,L | |
表选项
在表 1中,每个规则都是一个“If…Then…”的形式。对于不同的问题,一方面,可以合理选取pa和α0的取值范围;另一方面,根据问题的复杂程度,对pa和α0在模糊逻辑规则中稍加修正即可。
3 FGCS算法在可靠性分析中的应用结构机构可靠性问题可以表示为[15]

式中:μ为标准正态随机变量的向量形式;β为可靠性指标;g(μ)为极限状态方程。
在一些复杂的结构与机构中,极限状态方程往往是隐式的,为得到其显式形式,本文将利用神经网络响应面法构造极限状态方程。另外,为便于计算,采用了罚函数法将有约束的方程式(8)转化为以下无约束方程:

式中:ε为一个很大的正数,称为惩罚因子,文中将其设置为1010。
在利用FGCS算法计算可靠性指标β时,首先应根据式(9)得到可靠性指标β关于随机变量的方程后,将该方程作为适应度函数,然后通过FGCS算法对该适应度函数进行逐次迭代寻优。FGCS算法的计算步骤与CS算法和ICS算法相同,只是利用式(3)对保留下来的鸟窝进行更新,并通过模糊系统对pa和α0进行动态调整。通过迭代寻优,最后得到的全局最优解即为可靠性指标β。
4 算例分析为验证所提出的FGCS算法的性能,本文给出了3个算例,以PSO算法、CS算法、ICS算法和FGCS算法对各算例进行了计算效率和求解精度的对比分析,并对CS算法、ICS算法和FGCS算法的收敛性能做了比较。其中,前2个算例是用来考核求解可靠性分析方法的经典考题,后1个算例为本文所提算法在某型民机舱门锁定机构中的工程实际应用。所有算例均以MATLAB2009b为平台进行计算,操作系统为Windows 7,处理器为Inter(R) Core(TM) i5,3.19 GHz,内存3 GB。对所有算法,种群的规模为30,每种算法独立运行30次,最大迭代次数Kmax=1 000。在计算结果中,βavg、βmax和βmin分别表示β的平均值、最大值和最小值,Pf为βavg所对应的失效概率。
算例1 考虑两变量线性极限状态方程:g(X)=exp(0.2x1+6.2)-exp(0.47x2+5.0),其中各随机变量相互独立且服从标准正态分布。由自适应蒙特卡罗模拟得到的该问题的精确解为2.349 0,对应的失效概率为9.411 9×10-3[15]。该算例的计算结果及算法的收敛曲线分别如表 2和图 3所示。
表 2 算例1计算结果Table 2 Calculation results of example 1
| 计算方法 | β | P f/10 -3 | P f的计算误差/% | 计算用时/s | ||
| β min | β max | β avg | ||||
| PSO | 2.350 8 | 3.012 5 | 2.586 2 | 4.852 0 | 48.45 | 1.619 |
| CS | 2.349 3 | 2.413 9 | 2.353 5 | 9.298 8 | 1.202 | 1.075 |
| ICS | 2.349 3 | 2.365 1 | 2.351 8 | 9.341 4 | 0.749 | 1.038 |
| FGCS | 2.349 3 | 2.349 3 | 2.349 3 | 9.403 6 | 0.088 | 1.317 |
表选项
 |
| 图 3 算例1收敛曲线Fig. 3 Convergence curves of example 1 |
| 图选项 |
分析表 1中的计算结果可知,PSO算法的计算精度较低,容易陷入局部最优解,且计算用时最长,而另外3种算法的计算精度要明显优于PSO算法。虽然FGCS算法每次迭代计算的时间比CS算法和ICS算法的计算用时略长,但FGCS算法在每次迭代计算过程中均能得到精确解,失效概率的计算误差仅为0.088%,这说明了FGCS算法在对两变量线性极限状态方程可靠度进行分析的准确性。
从图 3中可以看出,在算例1中,FGCS算法的收敛性能要明显优于CS算法和ICS算法。在迭代次数大约进行到50次时,FGCS算法已收敛至全局最优解,而CS算法和ICS算法均要进行更多的迭代步骤才能收敛到全局最优解附近。同时分析表 2和图 3可知,FGCS算法用了非常少的迭代步骤就得到了全局最优解,且并没有消耗过多的计算时间,这充分体现了FGCS算法的优越性能。为显示FGCS算法的自适应特性,以该算例中搜索步长α0的动态变化过程为例加以展示,如图 4所示。
 |
| 图 4 搜索步长α0变化曲线Fig. 4 Changing curve of search step α0 |
| 图选项 |
由图 4可以看出,在总体趋势上,搜索步长α0随着迭代次数的增加而减小。α0之所以出现波动,是因为其还与鸟窝之间的欧式距离有关,α0减小也说明各鸟窝之间的分散性在减小。
算例2 考虑多变量极限状态方程:g(X)=x14/40+2x22+x3+3,式中各随机变量均服从标准正态分布。由蒙特卡罗法计算得到的该极限状态方程的精确解为3.000 0,对应失效概率为1.349 8×10-3[16]。该算例的计算结果分别如表 3和图 5所示。
表 3 算例2计算结果Table 3 Calculation results of example 2
| 计算方法 | β | P f/10 -3 | P f的计算误差/% | 计算用时/s | ||
| β min | β max | β avg | ||||
| PSO | 3.003 3 | 4.013 2 | 3.452 3 | 0.278 | 79.41 | 1.485 |
| CS | 3.001 5 | 3.313 3 | 3.099 2 | 0.970 | 28.14 | 1.010 |
| ICS | 3.000 0 | 3.079 2 | 3.014 8 | 1.285 | 4.774 | 1.072 |
| FGCS | 3.000 0 | 3.013 0 | 3.002 7 | 1.338 | 0.874 | 1.283 |
表选项
从表 3结果可以看出,对于多变量极限状态方程,虽然CS算法比PSO算法的计算效率和求解精度要高出很多,其计算出的可靠性指标的误差仅为3.308%,但是所对应失效概率的误差达到了28.14%。从计算结果中还可以看出,ICS算法和FGCS算法在求解此问题时都可以得到较优的解,但是FGCS算法的计算结果的精度要更胜一筹:从可靠性指标β的计算结果分析,FGCS算法得到的β与精确解之间的误差为0.090%,从对应的失效概率方面来看,误差仅为0.874%,说明求解精度非常高。另外,由于在100次迭代步骤之前3种算法都基本收敛到最优解,因此,为了将收敛曲线能够显示的更为清晰明了,此算例收敛对比曲线仅给出了前100次迭代的收敛性。从图 5的各种算法收敛性能对比曲线可以看出,ICS算法和FGCS算法很好地提高了CS算法的收敛性,但FGCS算法在大约仅进行了20次迭代后已收敛至最优解。此算例说明,在进行具有多变量的可靠性分析中,FGCS算法依然表现出非常出色的计算能力。
 |
| 图 5 算例2收敛曲线Fig. 5 Convergence curves of example 2 |
| 图选项 |
算例3 采用文献[17]分析的某型飞机手柄锁定机构(如图 6和图 7所示)作为工程算例对所提算法进行检验和对比。
 |
| 图 6 某民机舱门手柄机构Fig. 6 Handle mechanism of an aircraft door |
| 图选项 |
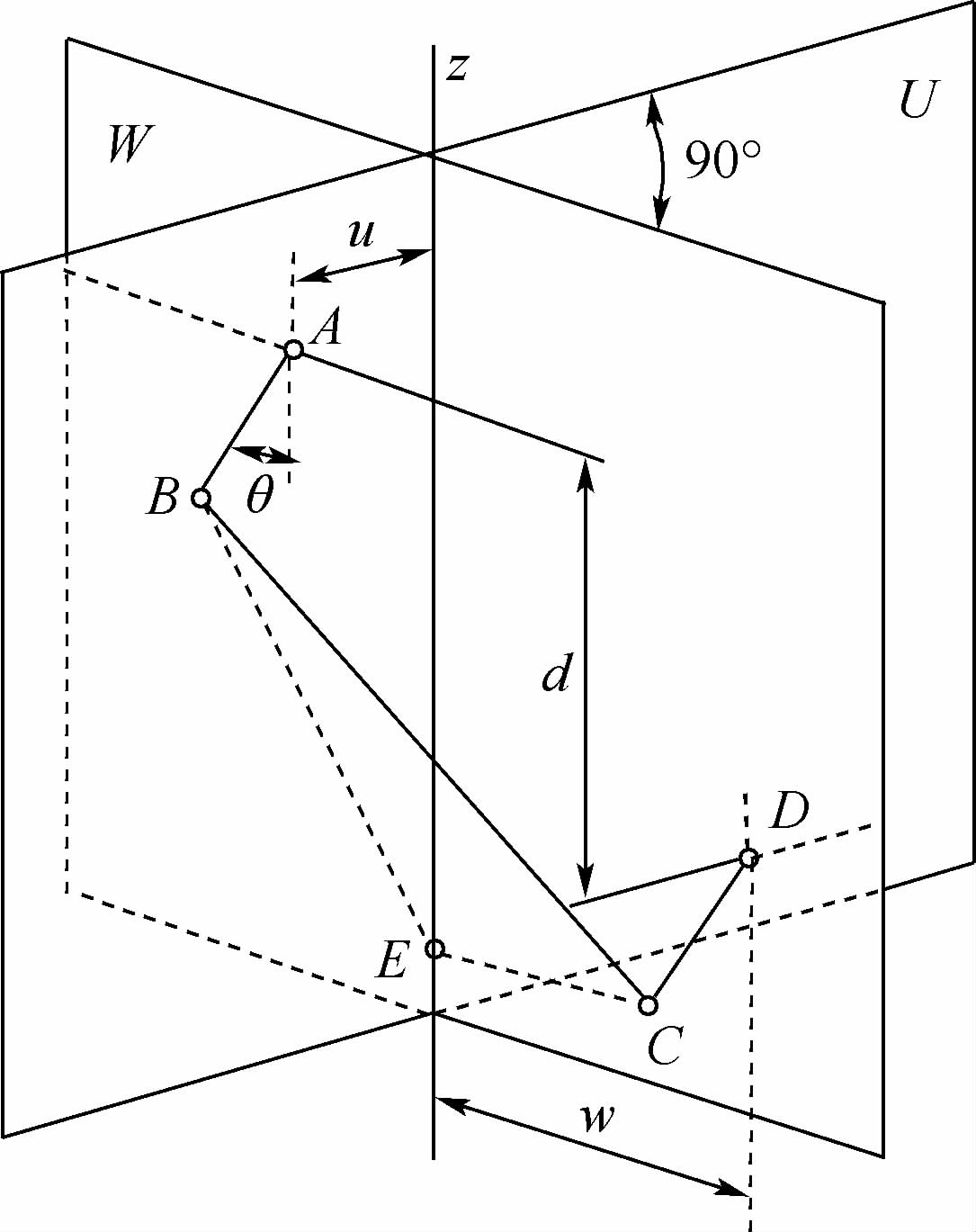 |
| 图 7 某民机舱门手柄机构示意图Fig. 7 Sketch of a handle mechanism of an aircraft door |
| 图选项 |
该机构利用空间四连杆机构过中心锁定原理对飞机舱门进行锁定,过中心锁定角度θ是各杆长和转轴之间距离的隐式函数,可表示为θ=f(l1,l2,l3,d,u,w)
式中:l1、l2、l3、d、u和w分别为各杆的长度、转轴之间的距离、转轴到运动平面交线之间的距离。机构完成锁定所要达到的锁定角度δ=4.00°,该问题的极限状态方程为g(l1,l2,l3,d,u,w)=θ-δ=f(l1,l2,l3,d,u,w)-4.00=0
假设该极限状态方程中所有随机变量均服从独立正态分布,它们的分布参数如表 4所示。
表 4 算例3中随机变量分布参数Table 4 Distribution parameters of random variables in example 3
| 随机变量 | 均值 | 变异系数 | 分布形式 |
| l1/mm | 120.0 | 0.01 | 正态分布 |
| l2/mm | 370.0 | 0.01 | 正态分布 |
| l3/mm | 115.0 | 0.01 | 正态分布 |
| d/mm | 320.0 | 0.01 | 正态分布 |
| u/mm | 19.0 | 0.01 | 正态分布 |
| w/mm | 96.0 | 0.01 | 正态分布 |
表选项
以文献[17]中通过蒙特卡罗法计算得到的可靠性指标作为该工程问题的精确解,β=4.364 3,对应的失效概率为6.376 6×10-6。利用各种算法计算得到的该空间四连杆机构的结果对比如图 8和表 5所示。
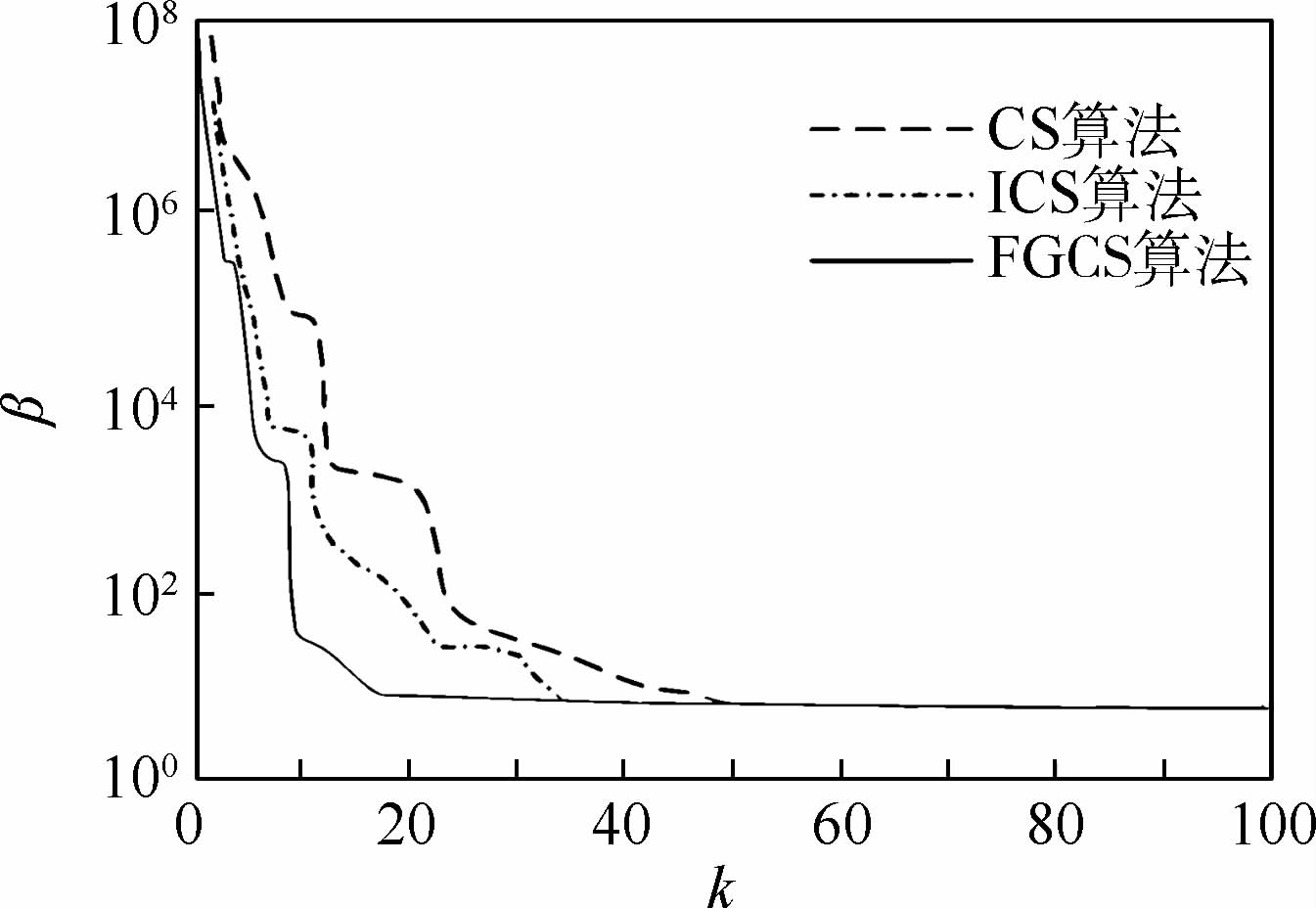 |
| 图 8 算例3收敛曲线Fig. 8 Convergence curves of example 3 |
| 图选项 |
表 5 算例3计算结果Table 5 Calculation results of example 3
| 计算方法 | β | P f/10 -6 | P f的计算误差/% | 计算用时/s | ||
| β min | β max | β avg | ||||
| PSO | 4.368 7 | 4.470 9 | 4.388 4 | 5.709 | 10.46 | 26.83 |
| CS | 4.368 7 | 4.371 2 | 4.369 1 | 6.238 | 2.175 | 59.54 |
| ICS | 4.368 7 | 4.369 4 | 4.368 8 | 6.247 | 2.040 | 61.25 |
| FGCS | 4.368 7 | 4.368 7 | 4.368 7 | 6.249 | 1.995 | 60.79 |
表选项
从表 5中各种算法的计算结果可以看出,4种算法均可计算得到该问题的全局最优解,其中PSO算法计算用时最短,但其得到的结果却误差较大,而CS算法、ICS算法和FGCS算法计算得到的可靠性指标值与精确解相比都属于高精度的解,但是FGCS算法在每次迭代计算中都可以收敛至全局最优解。在计算用时方面,FGCS算法在求解该问题时仅比CS算法多用了1.25 s,但比ICS算法用时要少。另外,图 8也只给出了前100次的收敛曲线,从图中可以看出,FGCS算法依然表现出非常好的收敛特性。通过该工程算例再次说明了FGCS算法在寻优迭代计算时的优越性,且该算法在解决以神经网络响应面法作为极限状态方程的情况下比其他3种算法得到的结果更为精确。
5 结论本文所提出的FGCS算法通过模糊逻辑规则对标准CS算法中的2个重要控制参数做了改进,并将具有全局最优导向的鸟窝更新公式引入到标准CS算法中。通过分析结果可知FGCS算法有以下几个优点:
1) 引入具有全局最优导向的公式后,CS算法的局部搜索能力得到加强,并且增加了鸟窝的多样性,有效地避免了算法陷入局部最优解。
2) 利用模糊逻辑规则动态地控制CS算法参数很好地权衡了标准CS算法的探索能力和开发能力。在迭代计算早期扩大搜索范围避免早熟现象,在迭代后期加速收敛性能。
3) 算例结果对比分析表明,在进行结构可靠性分析时,FGCS算法的求解精度与收敛速度要明显优于PSO算法、标准CS算法等。
参考文献
| [1] | YANG X S,DEB S.Cuckoo search via Lévy flights[C]//Proceeding of World Congress on Nature & Biologically Inspired Computing.Piscataway,NJ:IEEE Press,2009:210-214. |
| Click to display the text | |
| [2] | YANG X S,DEB S.Engineering optimisation by cuckoo search[J].International Journal of Mathematical Modeling and Numerical Optimisation,2010,1(4):330-343. |
| Click to display the text | |
| [3] | GANDOMI A H,YANG X S,ALAVI A H.Cuckoo search algorithm:A metaheuristic approach to solve structural optimization problems[J].Engineering with Computers,2013,29(2):17-25. |
| Click to display the text | |
| [4] | RADOVAN R B,STEVAN R D,VLADIMIR S D.Cuckoo search algorithm:A metaheuristic approach to solving the problem of optimum synthesis of a six-bar double dwell linkage[J].Mechanism and Machine Theory,2013,61:1-13. |
| Click to display the text | |
| [5] | KANAGARAJ G,PONNAMBALAM S G,JAWAHAR N.A hybrid cuckoo search and genetic algorithm for reliability redundancy allocation problems[J].Computers and Industrial Engineering,2013,66(4):1115-1124. |
| Click to display the text | |
| [6] | 秦强,冯蕴雯,薛小锋,等.基于改进布谷鸟算法的舱门锁定可靠性分析[J].航空计算技术,2014,44(1):23-26. QIN Q,FENG Y W,XUE X F,et al.Reliability analysis of door locking based on improved cuckoo algorithm[J].Aeronautical Computing Technique,2014,44(1):23-26(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [7] | ZHANG Y W,WANG L,WU Q D.Modified adaptive cuckoo search algorithm and formal description for global optimization[J].International Journal of Computer Applications in Technology,2012,44(2):73-79. |
| Click to display the text | |
| [8] | WALTON S,HASSAN O,MORGAN K,et al.Modified cuckoo search:A new gradient free optimisation algorithm[J].Chaos,Solitons and Fractals,2011,44(9):710-718. |
| Click to display the text | |
| [9] | VALIAN E,TAVAKOLI S,MOHANNA S,et al.Improved cuckoo search for reliability optimization problems[J].Computers and Industrial Engineering,2013,64(1):459-468. |
| Click to display the text | |
| [10] | 王李进,尹义龙,钟一文.逐维改进的布谷鸟搜索算法[J].软件学报,2013,24(11):2687-2698. WANG L J,YIN Y L,ZHONG Y W.Cuckoo search algorithm with dimension by dimension improvement[J].Journal of Software,2013,24(11):2687-2698(in Chinese). |
| Cited By in Cnki (13) | Click to display the text | |
| [11] | ZHU G P,KWONG S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation,2010,217(7):3166-3173. |
| Click to display the text | |
| [12] | RAJABIOUN R.Cuckoo optimization algorithm[J].Applied Soft Computing,2011,11(8):5508-5518. |
| Click to display the text | |
| [13] | PATRICIA M,FRUMEN O,OSCAR C,et al.Optimal design of fuzzy classification systems using PSO with dynamic parameter adaptation through fuzzy logic[J].Expert Systems with Applications,2013,40(8):3196-3206. |
| Click to display the text | |
| [14] | NIKNAM T,MOJARRAD H D,NAYERIPOUR M.A new fuzzy adaptive particle swarm optimization for non-smooth economic dispatch[J].Energy,2010,35(4):1764-1778. |
| Click to display the text | |
| [15] | KAYMAZ I.Application of kriging method to structural reliability problems[J].Structural Safety,2005,27(2):133-151. |
| Click to display the text | |
| [16] | 吕震宙,杨子政,赵洁.基于加权线性响应面法的神经网络可靠性分析方法[J].航空学报,2006,27(6):1063-1067. LU Z Z,YANG Z Z,ZHAO J.An artificial neural network method for reliability analysis based on weighted linear response surface[J].Acta Aeronautica et Astronautica Sinica,2006,27(6):1063-1067(in Chinese). |
| Cited By in Cnki (14) | Click to display the text | |
| [17] | 秦强,姚雄华,冯蕴雯,等.空间四连杆机构过中心锁定可靠性分析[J].机械强度,2014,36(5):710-715. QIN Q,YAO X H,FENG Y W,et al.Reliability analysis of over-center locking of spatial four-bar mechanism[J].Journal of Mechanical Strength,2014,36(5):710-715(in Chinese). |
| Cited By in Cnki |
