自1930年以来,铝合金加筋板一直作为飞行器主要承力结构[4]。加筋结构的主要破坏模式是丧失稳定性。崔德刚[5]系统研究了铆接和螺接加筋板结构的稳定性,并制定了设计手册;Aalberg等[6]从试验和工程算法方面研究2种焊接方式(MIG和FSW)对L型和帽型铝合金加筋板失稳和承载特性的影响;Paulo等[7]则对受初始几何扰动的铝合金加筋板轴压特性进行了数值分析,研究表明焊接成形加筋板热应力对其极限承载并无明显影响。
然而随着喷丸成形技术和蠕变时效成形技术的发展,大型加筋板结构一体成形得以实现[8, 9]。目前国内外对于一体成形的铝合金加筋板结构轴压稳定性和承载能力的研究甚少,尤其对侧边受到约束的加筋板轴压特性缺乏研究[10]。
本文利用试验和数值模拟手段,对不同侧边约束下的铝合金加筋板结构轴压屈曲和后屈曲特性进行研究,探讨铝合金加筋板结构轴向压缩下蒙皮筋条损伤破坏机理。研究结果可为铝合金加筋板结构设计和分析提供一定的参考。
1 试验对象及方法试验选用铝合金加筋板为典型的五筋条结构形式,筋条剖面为工型,试验件基本尺寸如图 1所示,其中加筋板两端各有50 mm加载过渡区,图中尺寸单位均为mm。试验件共5件,采用铝合金(δ457B04)整体加工成形。
 |
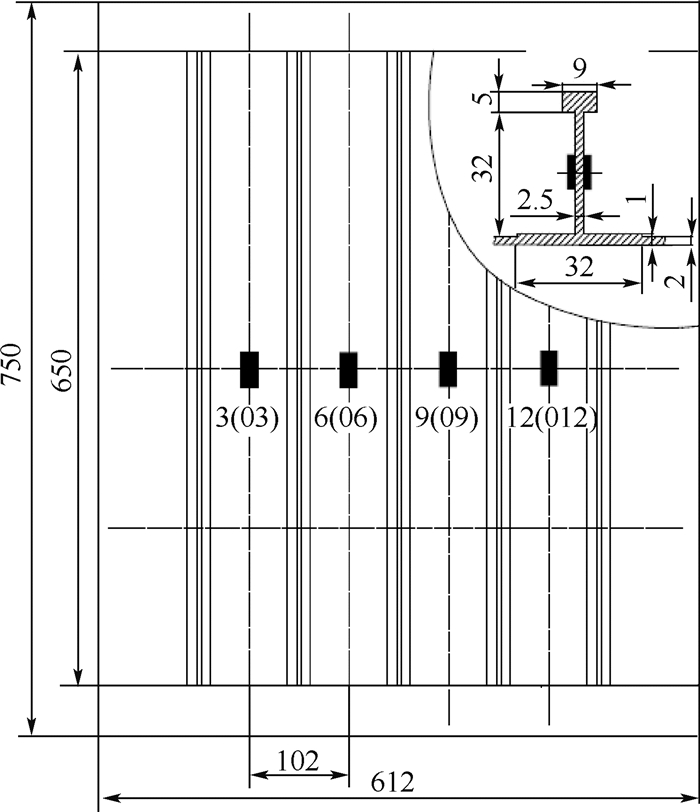| 图 1 加筋板试验件示意图Fig.1 Schematic diagram of stiffened panels |
| 图选项 |
首先进行试样拉伸试验,为后续有限元模拟提供相关参数。Clarke[11]以及Tryland等[12]采用从加筋板上不同部位切取试样件进行标准拉伸试验。朱浩等[13]进行了平板拉伸试验及蝶型试样拉伸试验,测得该铝合金在不同应力状态和不同应变率下的材料力学性能。本文试样件分为平板和蝶型试样件,均取自第1件加筋板蒙皮壁板和筋条腹板。图 2所示为拉伸试样件示意图,图中尺寸单位均为mm。
 |
| 图 2 拉伸试样件示意图Fig.2 Schematic diagram of tensile specimen |
| 图选项 |
使用济南时代试金仪器有限公司的WDW-200E万能试验机进行试样拉伸试验,WAW-2000E试验机进行加筋板轴压试验。加筋板轴压试验中,活动U型铝槽内套活动钢制垫块可保证侧边完全约束,垫块圆弧形刀口提供简支约束,约束距侧边沿12 mm。对第2~3件试验件重点位置布置应变计以监测加载过程中试验件的变形,试验测点布置方案如图 1所示,在试验件中部蒙皮与筋条腹板正反面布置电阻式应变计并编号,图中带括号编号表示无筋条一侧应变测点,5根筋条的腹板应变测点编号依次为1、2,4、5,7、8,10、11,13、14。将第4~5件试验件无筋条一侧用白色哑光漆处理,以光测实验力学中的影像云纹法为理论基础[14],建立一套光测系统,实现对试验件失稳模态的实时监测,光测系统及现场如图 3所示。成熟的成形工艺使得铝合金加筋板轴压试验结果高度一致,分散性小,典型试验结果在本文第3节与数值模拟结果一起给出。
 |
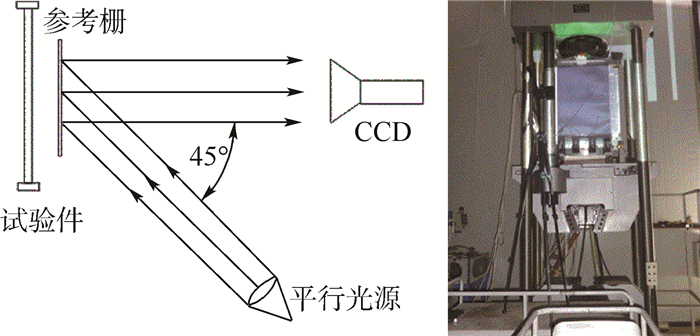| 图 3 云纹系统及测试现场Fig.3 Moiré interferometry system and test site |
| 图选项 |
2 有限元模型2.1 铝合金材料本构模型在黏弹性力学和连续介质损伤力学的基础上,考虑材料的大变形、高应变速率和绝热的条件下,Johnson和Cook于1983年提出一个经验性本构模型,该模型认为,材料的屈服流变应力σ可以表示为应变ε、应变率
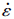和温度T*的函数[15]: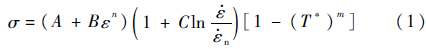
式中:
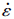n为参考应变率;A、B、C、n和m为系数。本文未考虑温度影响项T*。通过试样拉伸试验可确定式(1)中相关系数。图 4所示为平板拉伸试验所得工程应力-应变曲线。结合图 5(b)曲线拟合得到材料本构方程为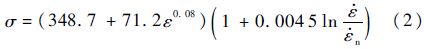
 |
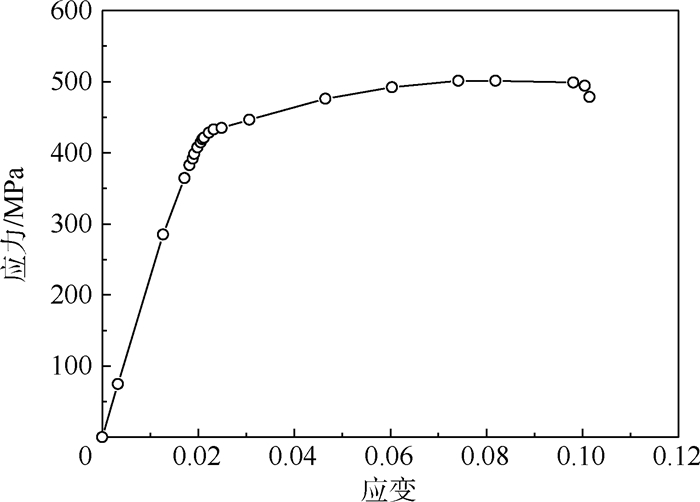| 图 4 平板拉伸工程应力-应变曲线Fig.4 Engineering stress-strain curves for tensile panels |
| 图选项 |
2.2 铝合金材料损伤模型韧性材料的断裂主要有2种机理:材料空隙聚集成核引起韧性断裂和局部剪切硬化引起剪切断裂。Hooputra等[16]针对这2种损伤机理,提出相应的损伤模型。
韧性断裂准则:
剪切断裂准则:
式中:ωD为韧性断裂准则值,韧性等效塑性应变
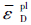与三轴应力度η和等效塑性应变率
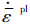相关;ωS为剪切断裂准则值,剪切等效塑性应变
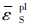与剪切应力比θS和等效塑性应变率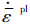相关。当准则值ωD、ωS达到1时,材料出现相应损伤。通过试样拉伸试验测得三轴应力度η和等效塑性应变率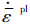等相关参数。图 5(a)所示为不同三轴应力度下应力-应变曲线,图 5(b)所示为不同应变率下应力-应变曲线。 |
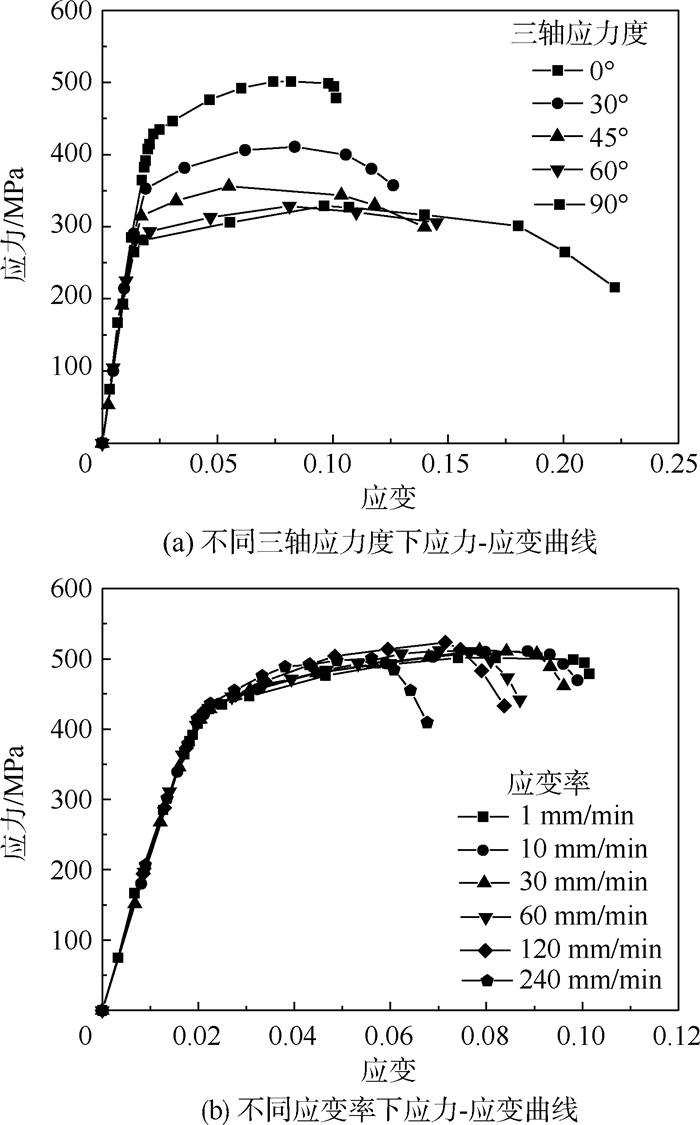| 图 5 铝合金材料损伤参数测定试验Fig.5 Damage parameters test for aluminum alloys materials |
| 图选项 |
损伤起始后,材料进入损伤演化阶段,材料刚度逐渐下降,直到刚度为零,代表损伤区域完全破坏。本文采用基于位移的线性损伤演化准则。铝合金材料线性损伤演化模型如图 6所示。当有效塑性位移达到给定值时,即
=
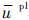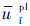(本文参考文献[16]取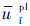=0.1)时,材料刚度衰减至零。 |
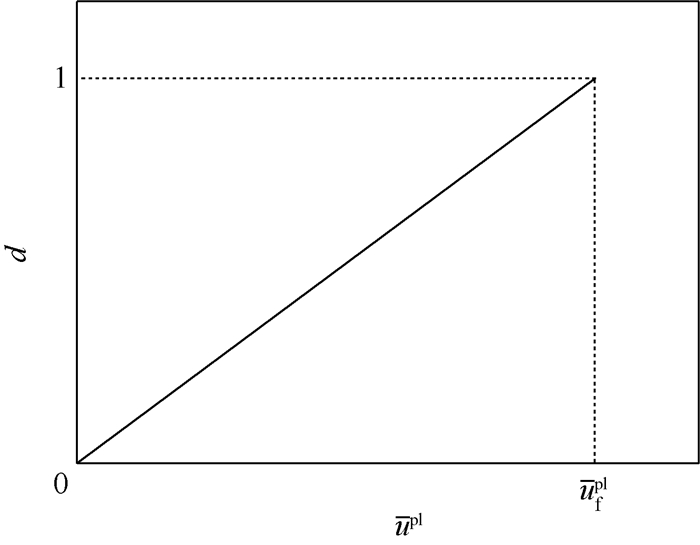| 图 6 铝合金材料线性损伤演化模型Fig.6 Linear damage propagation model of aluminum alloys materials |
| 图选项 |
2.3 有限元模型建立使用ABAQUS软件建立有限元模型如图 7所示,蒙皮与筋条采用线性减缩积分四边形壳单元(S4R),约9 000个。蒙皮和筋条之间通过绑定约束(Tie)连接,因此在线性特征值分析中不会出现嵌入现象。将加筋板模型两端与特征点耦合(Couple),一端施加固支约束,另一端仅放开加载方向自由度。侧边简支模型在相应位置通过位移限制约束模拟简支边界作用,侧边自由模型两侧边无限制约束。
 |
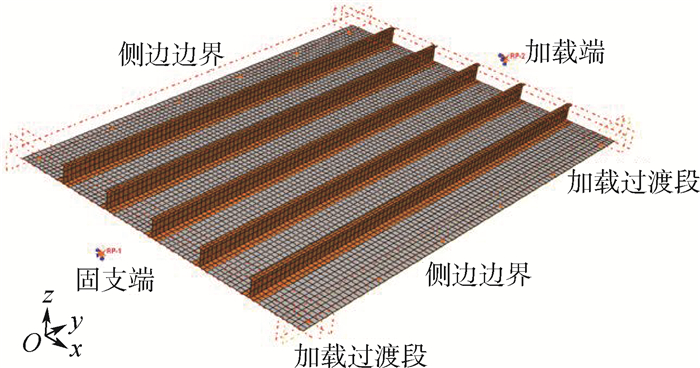| 图 7 加筋板有限元模型Fig.7 Finite element model of stiffened panels |
| 图选项 |
3 结果及分析典型铝合金加筋板轴压载荷-位移曲线如图 8所示,结合图 9应变数据可将曲线分为3个阶段:线性屈曲阶段,起始载荷随着压缩位移线性增大;直至蒙皮出现局部失稳(A点),结构主要依靠筋条承载而进入非线性后屈曲阶段,蒙皮失稳变形增大导致筋条扭转(B点),结构刚度进一步下降直至筋条腹板根部折断,结构失去承载能力;破坏后阶段,材料塑性变形使得结构破坏瞬间承载并未突降。
 |
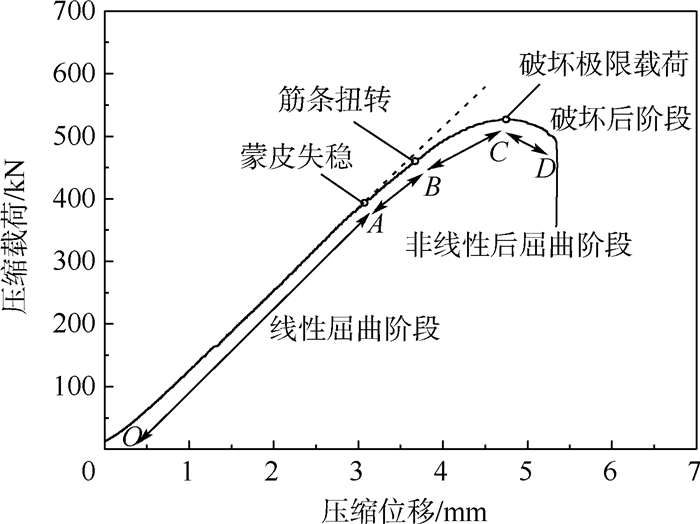| 图 8 铝合金加筋板轴压载荷-位移曲线Fig.8 Compression load-displacement curve of aluminum alloys stiffened panels |
| 图选项 |
 |
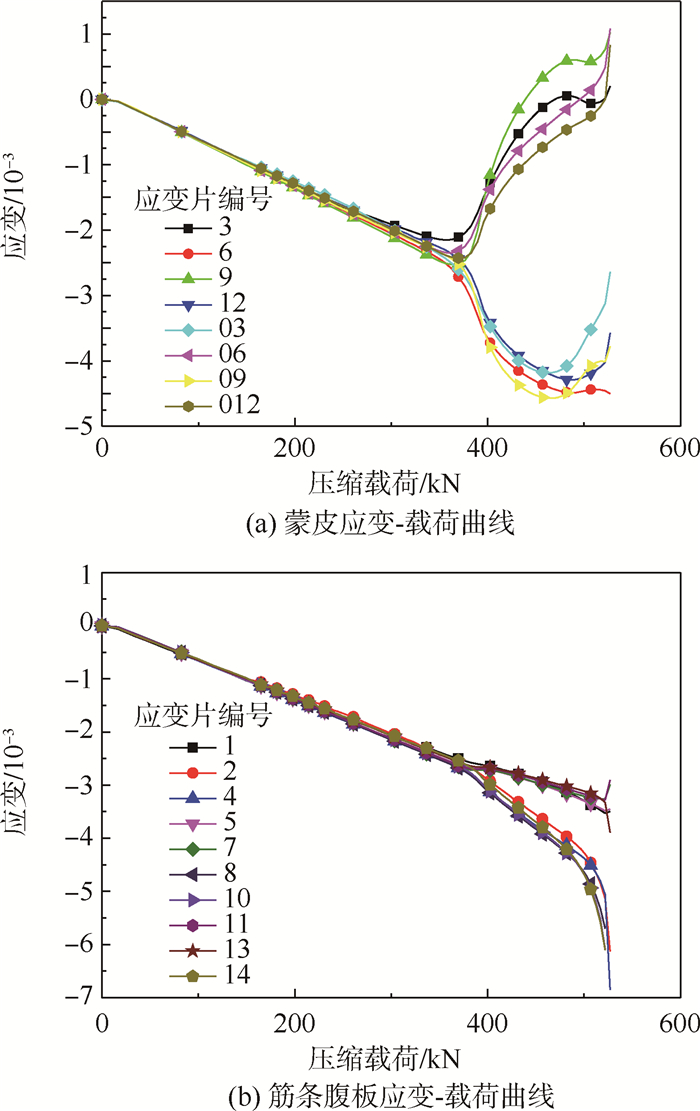| 图 9 铝合金加筋板典型应变结果Fig.9 Typical test results of strain on aluminum alloys stiffened panels |
| 图选项 |
3.1 压缩失稳特性试验中根据云纹图像可以直观确定失稳模态及失稳载荷,图 10所示为侧边简支加筋板试验件失稳模态形成过程。当压缩载荷超过试验件的临界失稳载荷时,蒙皮表面平行条纹开始出现扭曲,逐渐形成马鞍形条纹,即蒙皮发生局部失稳。在后屈曲承载阶段,蒙皮面外变形逐渐增大,云纹图像表现为新条纹吐出,最终形成稳定的纵向7个半波失稳模态。数值模拟如图 11所示。图 11(a)为侧边简支加筋板失稳模态,蒙皮同时失稳,表现为纵向7个半波,失稳载荷为356 kN,与试验结果吻合;图 11(b)为侧边自由加筋板失稳模态,蒙皮两侧边首先发生失稳,表现为纵向4个半波,失稳载荷为71 kN,远小于侧边简支加筋板。
 |
| 图 10 侧边简支加筋板试验件失稳模态形成过程Fig.10 Developing process of buckling mode for stiffened panels with side simply support |
| 图选项 |
 |
| 图 11 加筋板失稳模态计算结果Fig.11 Calculation results of buckling mode for stiffened panels |
| 图选项 |
3.2 后屈曲承载能力加筋板蒙皮局部失稳后,结构继续承载进入后屈曲阶段,随后蒙皮凹凸变形使得筋条扭转,后屈曲阶段结构承载呈非线性增加直至破坏,侧边简支与侧边自由加筋板破坏模式相似,均表现为筋条腹板根部折断,蒙皮向外凸出,5根筋条相向弯曲变形,图 12所示为加筋板试验件典型压缩破坏模式。数值模拟也得到了一致的破坏模式,如图 13所示。
 |
| 图 12 加筋板典型压缩破坏模式Fig.12 Photographs of typical failure mode of stiffened panels in compression |
| 图选项 |
 |
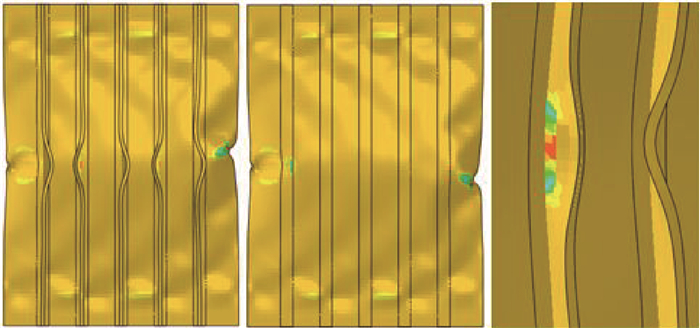| 图 13 数值模型破坏模式Fig.13 Calculation results of failure mode |
| 图选项 |
试验与数值模拟计算结果统计如图 14所示,可知数值模拟有效地得到了相近的屈曲载荷和后屈曲承载能力;侧边自由加筋板失稳载荷虽然远低于侧边简支加筋板失稳载荷,但其结构破坏强度仅下降约9%,这是由于加筋板结构主要依靠筋条承载,而侧边蒙皮的先失稳并不能显著影响筋条扭转变形。
 |
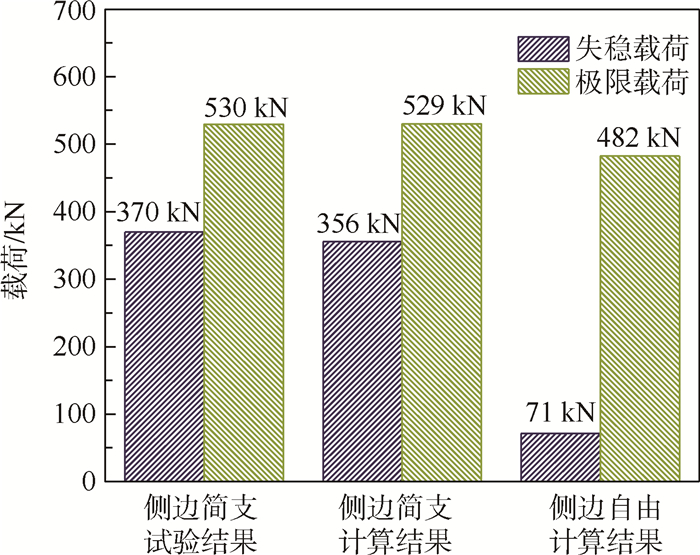| 图 14 铝合金加筋板试验和计算结果Fig.14 Test and calculation results of aluminum alloys stiffened panels |
| 图选项 |
4 结 论1) 基于ABAQUS建立含韧性损伤和剪切损伤的Johnson-Cook本构模型,可以模拟铝合金加筋板的后屈曲过程,模拟结果与试验结果相吻合。
2) 典型铝合金加筋板轴压载荷-位移曲线以蒙皮局部失稳和破坏极限为界可分为3个阶段。
3) 试验和计算均表明,侧边简支加筋板蒙皮同时发生失稳,且表现为纵向7个半波;而侧边自由加筋板侧边蒙皮首先发生失稳,表现为纵向4个半波,且失稳载荷远低于侧边简支加筋板。
4) 侧边自由加筋板失稳载荷虽远低于侧边简支加筋板失稳载荷,但其结构破坏强度仅下降约9%。
参考文献
| [1] | 杜善义,关志东.我国大型客机先进复合材料技术应对策略思考[J].复合材料学报,2008,25(1):1-10. DU S Y,GUAN Z D.Strategic considerations for development of advanced composite technology for large commercial aircraft in China[J].Acta Materiae Compositae Sinica,2008,25(1):1-10(in Chinese). |
| Cited By in Cnki (102) | |
| [2] | DURSUN T,SOUTIS C.Recent developments in advanced aircraft aluminum alloys[J].Materials & Design,2014,56(4):862-871. |
| Click to display the text | |
| [3] | HEINZ A,HASZLER A,KEIDEL C,et al.Recent development in aluminum alloys for aerospace applications[J].Materials Science and Engineering:A,2000,280(1):102-107. |
| Click to display the text | |
| [4] | STARKE E A,STALEY J T.Application of modern aluminum alloys to aircraft[J].Progress in Aerospace Science,1996,32(2-3):131-172. |
| Click to display the text | |
| [5] | 崔德刚.结构稳定性设计手册[M].北京:航空工业出版社,1996:165-208. CUI D G.Design manual for structural stability[M].Beijing:Aviation Industry Press,1996:165-208(in Chinese). |
| [6] | AALBERG A,LANGSETH M,LARSEN P K.Stiffened aluminum panels subjected to axial compression[J].Thin-Walled Structures,2001,39(10):861-885. |
| Click to display the text | |
| [7] | PAULO R M F,TEIXEIRA-DIAS F,VALENTE R A F.Numerical simulation of aluminum stiffened panels subjected to axial compression:Sensitivity analyses to initial geometrical imperfections and material properties[J].Thin-Walled Structures,2013,62(1):65-74. |
| Click to display the text | |
| [8] | 曾元松,黄遐.大型整体壁板成形技术[J].航空学报,2008,29(3):721-727. ZENG Y S,HUANG X.Forming technologies of large integral panel[J].Acta Aeronautica et Astronautica Sinica,2008,29(3):721-727(in Chinese). |
| Cited By in Cnki (73) | |
| [9] | 李劲风,郑子樵,李世晨,等.铝合金时效成形及时效成形铝合金[J].材料导报,2006,20(5):101-103. LI J F,ZHENG Z Q,LI S C,et al.Age forming of Al alloys and ageformable Al alloys[J].Materials Review,2006,20(5):101-103(in Chinese). |
| Cited By in Cnki (48) | |
| [10] | 邵青,何宇廷,张腾,等.侧边边界条件对复合材料加筋板轴压载荷下屈曲后屈曲性能的影响[J].复合材料学报,2014,31(3):741-748. SHAO Q,HE Y T,ZHANG T,et al.Influence of side boundary condition on buckling and post-buckling performance of composite stiffened panels under axial compression load[J].Acta Materiae Compositae Sinica,2014,31(3):741-748(in Chinese). |
| Cited By in Cnki | |
| [11] | CLARKE J D.Buckling of aluminum alloy stiffened plate ship structure[M]//NARAYANAN R.Aluminum atructures-advances design and construction.Amsterdam:Elsevier,1987:81-92. |
| [12] | TRYLAND T,HOPPERSTAD O S,LANGSETH M.Design of experiments to identify material properties[J].Materials & Design,2000,21(5):477-492. |
| Click to display the text | |
| [13] | 朱浩,朱亮,陈剑虹.应力三轴度和应变率对6063铝合金力学性能的影响及材料表征[J].材料科学与工程学报,2007,25(3):358-362. ZHU H,ZHU L,CHEN J H.Influence of stress triaxiality and strain rate on the mechanics behavior of 6063 aluminum alloy and material characterization[J].Journal of Materials Science & Engineering,2007,25(3):358-362(in Chinese). |
| Cited By in Cnki (29) | |
| [14] | 戴福隆,沈观林,谢惠民.实验力学[M].北京:清华大学出版社,2010:367-385. DAI F L,SHEN G L,XIE H M.Experimental mechanics[M].Beijing:Tsinghua University Press,2010:367-385(in Chinese). |
| [15] | ZHANG D N,SHANGGUAN Q Q,XIE C J,et al.A modified Johnson-Cook model of dynamic tensile behaviors for 7075-T6 aluminum alloy[J].Journal of Alloys and Compounds,2015,619:186-194. |
| Click to display the text | |
| [16] | HOOPUTRA H,GESE H,DELL H,et al.A comprehensive failure model for crashworthiness simulation of aluminum extrusions[J].International Journal of Crashworthiness,2004,9(5):449-463. |
| Click to display the text |
