目前,对于采用电阻补偿网络的模拟温补晶振,当要求工作在-40~+70℃或者更宽的温度范围内,且频率温度稳定性要达到±1×10-6时,一次温度补偿的成功率较低.一般首次安装温度补偿网络后,还需再经过2~3次网络参数调节才能使晶体振荡器的频率温度稳定性满足指标要求,既降低生产效率,又影响产品可靠性.对此,本文针对一次补偿成功率低的问题,分析了影响温度补偿效果的因素,并在此基础上提出改进的温度补偿方法[16].
1 模拟温补原理及分析1.1 模拟温补晶振工作原理采用电阻温补网络的模拟温补晶振由振荡电路、变容二极管和电阻温补网络3个部分组成,如图 1所示.其中,电阻温补网络常采用桥式网络型式,由负温度系数热敏电阻和固定电阻构成.
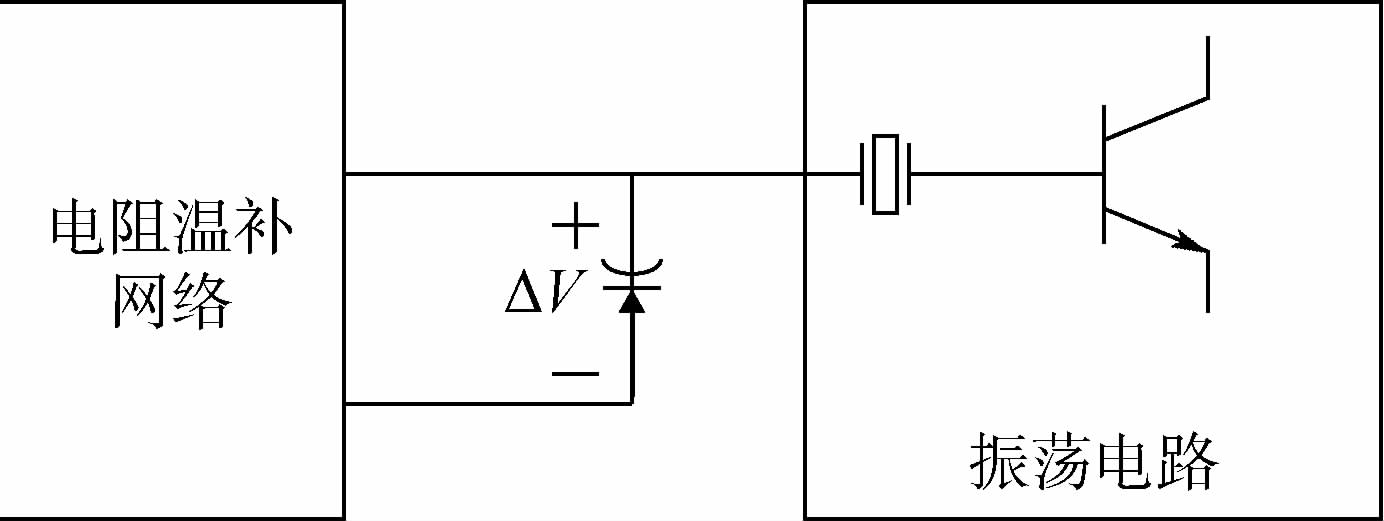 |
| 图 1 模拟温补晶振工作原理框图 Fig. 1 Analog TCXO working principle block diagram |
| 图选项 |
工作时,温补网络产生与晶体振荡器温频曲线形状相反的电压温度曲线,并将其施加到变容二极管上,调节振荡频率使发生恰好反向于温频特性的变化,从而实现温度补偿,如图 2所示.
 |
| 图 2 模拟温度补偿原理 Fig. 2 Analog temperature compensation principle |
| 图选项 |
因此,温度补偿的关键就是通过补偿网络计算程序确定一组电阻值,使补偿网络的实际发生电压与理想补偿电压之间的拟合误差最小.
1.2 温补精度影响因素分析传统温度补偿方法一次成功率低,主要是由于补偿网络计算程序中热敏电阻模型不精确.
传统补偿方法中,热敏电阻在窄温范围内测试,并使用式(1)进行建模.

式中:T0和T为绝对温度,T0=298.15K,T为当前温度;R0为T0时的电阻值;B为材料常数.
当温度范围很宽时,式(1)中的计算模型不适用,而应如式(2)所示.
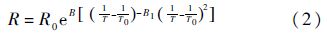
式中:B1为高阶材料常数[17].
此外,传统方法中热敏电阻温度特性是在近似零功率条件下测量并计算或拟合得到的.实际上,热敏电阻在温补网络中工作时并不能很好地满足零功率条件.由于热敏电阻具有耗散系数,因此消耗在热敏电阻中的能量会引起温升导致电阻值改变.而且,电路中还有其他器件或多或少的辐射热量,引起温度梯度.因而,热敏电阻的计算模型和实际使用情况存在较大差距.如果将式(1)的热敏电阻模型代入温补网络计算程序,必然引起大的误差,造成实际补偿效果恶化.
2 改进的温度补偿方法新的模拟温补晶振宽温补偿方法从热敏电阻建模和补偿网络计算程序两个方面进行改进.
2.1 热敏电阻建模改进温度补偿方法中,热敏电阻采用在线测量和比例建模的方式.
首先,热敏电阻测量中使用与补偿网络相同的电路形式和大致相当的电路参数,以及宽温测试范围,即尽量接近其实际使用情况,而非在零功率和窄温条件下测量,如图 3所示.其中,电阻符号上带箭头的为热敏电阻(R4、R5、R7),其余为固定电阻(R1~R3、R6、R8).
其次,在测试过程中,随温度变化,记录图 3中各节点电压.对于N个温度测试点,Vz、V1、V2、V3、V4均为N维行向量.
然后,根据节点电压和基尔霍夫定律、诺顿定律计算得到各热敏电阻随温度变化的电阻值,并将热敏电阻值表示为N维向量R1×N.
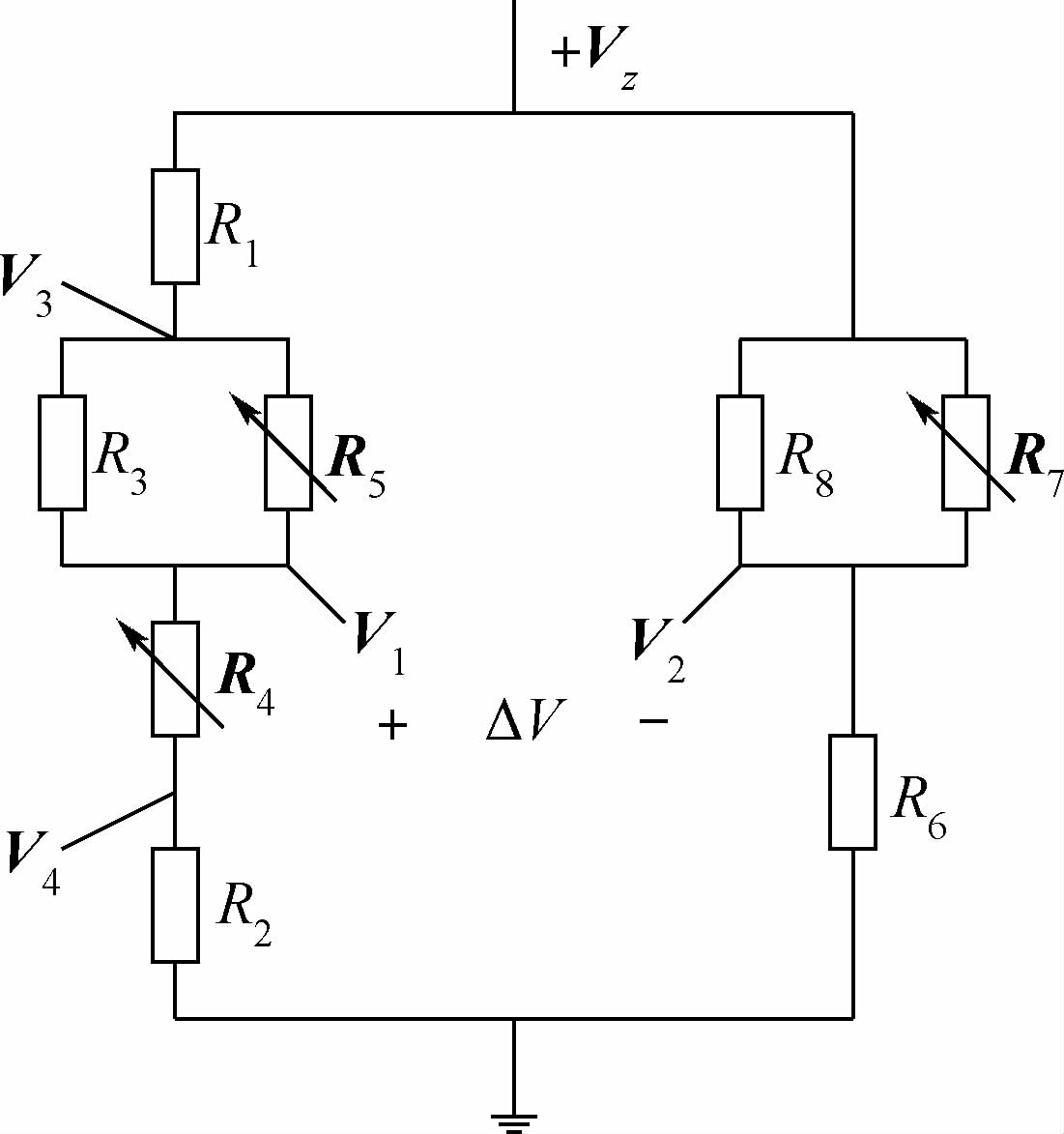 |
| 图 3 热敏电阻在线测量网络 Fig. 3 On-line test network for thermistors |
| 图选项 |
最后,将得到的热敏电阻向量代入温补网络计算程序中使用.实际上,考虑到同批次热敏电阻具有较好的一致性和工程应用的简便性,可以采用热敏电阻比例建模的方式.不必每只待使用的热敏电阻都按图 3进行实际测量,而是将上述测试完成的热敏电阻作为参考热敏电阻,其余相同类型、阻值相近的热敏电阻建模为
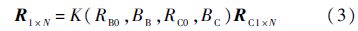
式中:K(RB0,BB,RC0,BC)为与待使用热敏电阻和参考热敏电阻特性参数相关的比例系数;RB0和BB为待使用热敏电阻特性参数;RC0和BC为参考热敏电阻特性参数,均可由传统测试方法得到或厂家给出;RC1×N为参考热敏电阻实测值,R1×N和RC1×N均为N维行向量.
2.2 补偿网络计算程序 将式(3)建模的热敏电阻代入温补网络计算程序中.温补网络输出电压ΔV为N维行向量,由图 3可得
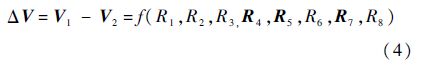
V1、V2和ΔV的第k个分量表达式为
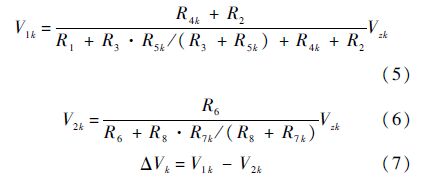
可见,V1、V2和ΔV均为各电阻值的非线性函数.
使振荡器温频特性得到完全补偿的网络电压为目标补偿电压ΔM,N维行向量.改进方法中,温补网络计算程序采用遗传算法,通过优化计算求得一组网络参数值,使网络实际输出电压ΔV与目标补偿电压ΔM之间的拟合误差最小.
在算法中,染色体编码采用实数编码,将固定电阻值或固定电阻值和待使用热敏电阻特性参数RB0、BB作为基因,依次排列构成染色体.
为了增强程序的实用性,目标函数包括3部分:残差平方和、最大偏差和常温频率准确度.这3部分通过罚函数来折中[18].
残差平方和表达式为
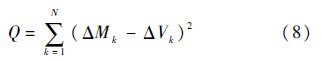
最大偏差表达式为
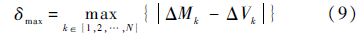
常温频率准确度的表达式为
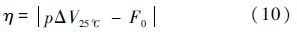
式中:p为压控灵敏度;ΔV25℃为25℃时补偿网络输出电压;F0为振荡器标称频率.
在计算过程中通过选择、交叉、变异等步骤,得到进化的染色体.并且,为了克服进化过程中的早熟和欺骗问题,获得最佳结果,根据进化的不同阶段,设置不同的群体选择压力,并实施最优保存策略[19].
3 验证试验3.1 热敏电阻计算根据热敏电阻在线测量和比例建模方法,分别将2组各3只热敏电阻连接到图 3的测量网络中,在-40~+70℃范围内进行测量.
然后,将第1组中的3只热敏电阻作为对应网络位置的参考热敏电阻.将第2组的3只热敏电阻分别按照式(3)进行建模计算,建模计算值与其实测值和传统方法计算值的比较结果如图 4所示.
 |
| 图 4 热敏电阻计算值与测试值比较 Fig. 4 Comparison between compute values and test value of thermistor |
| 图选项 |
由图 4可见,相比于传统方法,采用改进温度补偿方法计算得到热敏电阻值更接近于实测值.因此,将该计算值代入温补网络计算程序可以有效提高计算准确度.
3.2 补偿网络参数计算选取10只10MHz晶体振荡器进行温度补偿.要求补偿后的晶体振荡器在-40~+70℃的范围内频率温度稳定性达到±1×10-6.
首先,选取10组热敏电阻,分别按式(3)进行建模,其中参考热敏电阻与第3.1节中参考热敏电阻相同.
然后,将建模的热敏电阻代入温补网络计算程序,并将待计算的固定电阻值按顺序排列,组成实数编码的染色体.在进化过程中,采用随进化代数变化的交叉概率pc和变异概率pm.
目标函数表示为
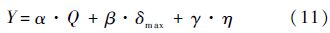
式中:α、β、γ分别为Q、δmax和η的权重.
迭代计算过程如图 5所示,经过多次迭代计算达到收敛条件后,便得到一组最优的固定电阻值.为了进一步优化计算结果,计算程序中也可以将固定电阻和热敏电阻特性参数RB0和BB同时作为待优化量进行实数编码和优化计算.
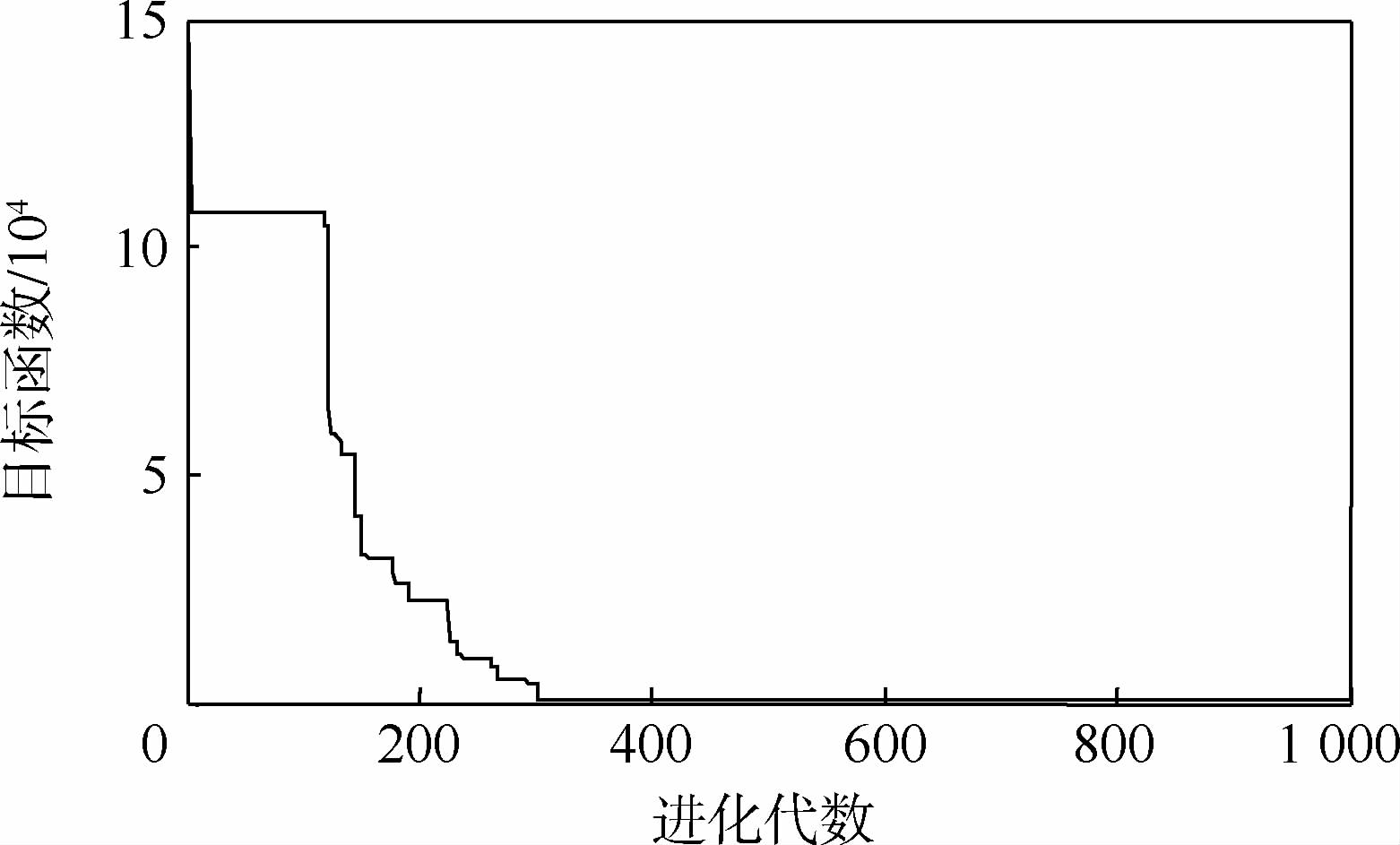 |
| 图 5 补偿网络计算程序迭代过程 Fig. 5 Iteration process of compensation network computing program |
| 图选项 |
3.3 频率温度稳定性测试根据温补网络计算程序得到的固定电阻值,安装温补网络.由于计算程序得出的电阻值通常为几kΩ~几百kΩ的任意实数,而实际电阻值为一系列离散值.因此,安装时为了尽量接近计算值,网络中每一个计算电阻由两个实际电阻组合而成,并且组合精度不应低于1%.
将装配完的10只晶体振荡器放入温箱,进行频率温度稳定性测试,测试结果如表 1所示.表 1中同时给出了采用传统补偿方法进行计算和装配后的实测结果.
表 1 传统方法与改进方法测试结果对比Table 1 Results comparison between traditional method and modified method
| 晶振序号 | 频率温度稳定性/10-6 | |
| 传统方法一次温度补偿结果 | 改进方法一次温度补偿结果 | |
| 1 | 3.504 | 1.000 |
| 2 | 2.471 | 0.897 |
| 3 | 1.933 | 0.738 |
| 4 | 3.488 | 0.815 |
| 5 | 1.671 | 0.613 |
| 6 | 2.505 | 0.758 |
| 7 | 1.985 | 0.847 |
| 8 | 2.224 | 0.737 |
| 9 | 1.405 | 0.572 |
| 10 | 0.996 | 0.521 |
表选项
可见,采用改进方法,10只晶振进行一次温度补偿后,频率温度稳定性均达到并优于±1×10-6.以3号晶体振荡器为例,分别采用传统方法和改进方法进行一次温度补偿后,得到频率温度稳定性如图 6所示.补偿前3号晶体振荡器的频率温度稳定性约为±15×10-6.
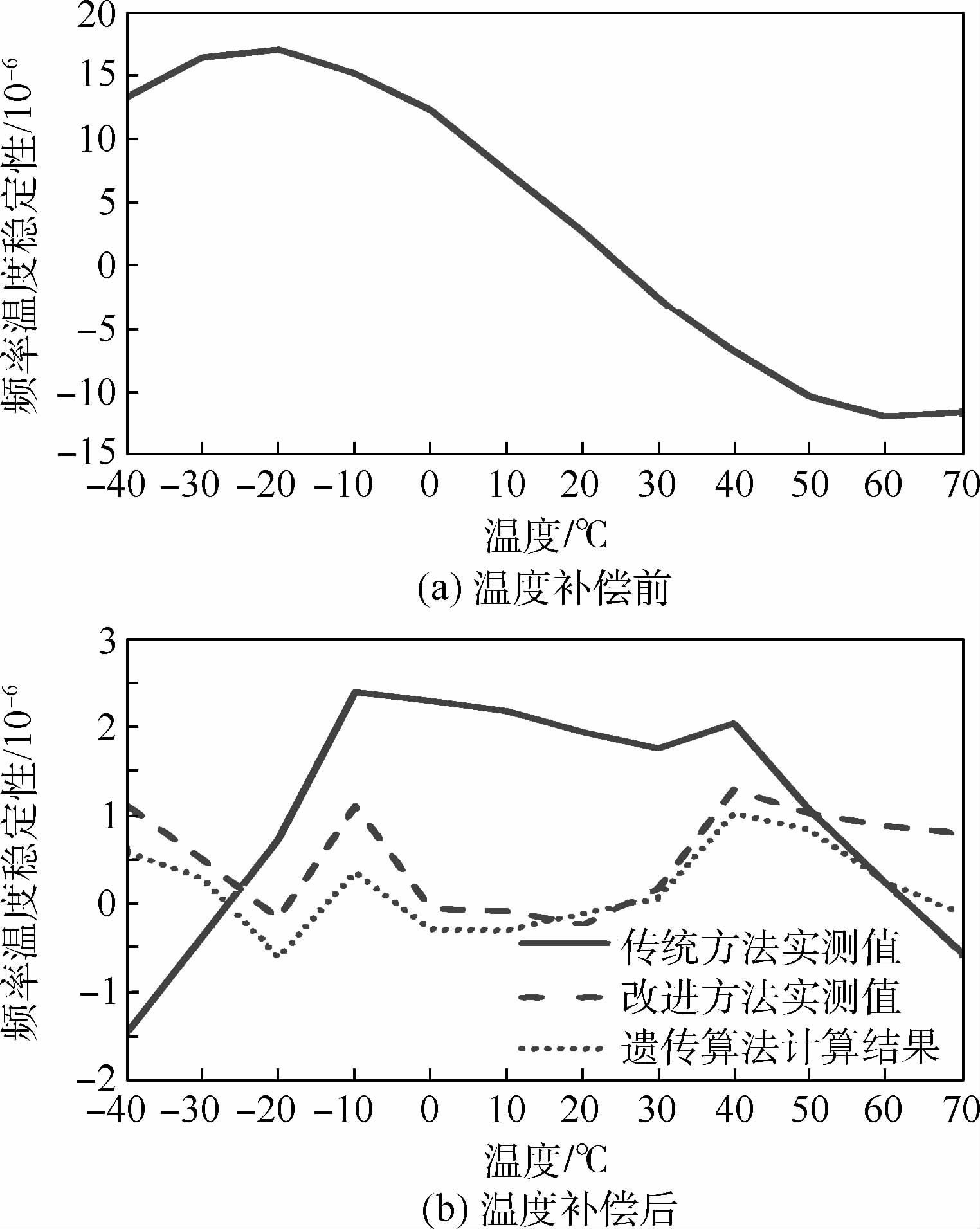 |
| 图 6 3号晶振一次温度补偿结果 Fig. 6 Result of once temperature compensation for oscillator No.3 |
| 图选项 |
综合表 1和图 6表明,采用改进方法进行一次温度补偿的效果明显优于传统方法,不仅频率波动大大减小,而且常温下的频率准确度也明显提高.因此,改进方法可显著提高晶体振荡器的一次温度补偿成功率.
4 结 论综上所述,本文提出了一种改进的模拟温补晶振宽温范围温度补偿方法.
1) 改进方法中,热敏电阻采用在线测试和比例建模,并将建模的热敏电阻代入温补网络计算程序,提高了补偿网络参数计算的准确度.
2) 温补网络计算程序中,通过遗传算法优化获得网络参数解.该算法可适用多种复杂约束条件,且不依赖于初始解,因此使用灵活.
3) 经试验验证,该方法可以有效提高温度补偿精度和一次温补成功率,避免多次补偿带来的人员和设备占用,以及引入的不确定因素,因此可显著提升生产效率和产品可靠性.
致谢 感谢刘宇婧和邢树来同志在项目研究过程中给予的支持和帮助.
参考文献
| [1] | GJB 1648A—2011.晶体振荡器通用规范[S].北京:总装备部军标出版发行部,2011:47. GJB 1648A—2011.General specification for crystal oscillators[S].Beijing:General Armament Department Military Standard Publishing Department,2011:47(in Chinese). |
| [2] | John R V.Introduction to quartz frequency standards,AD-A248503[R].NJ:US Army LABCOM ETDL,1992:22-28. |
| [3] | 吴剑强.小型超宽温度范围模拟温补晶振[J].湖南大学学报,1993,20(6):34-38. Wu J Q.The miniature temperature compensation crystal oscillator for ultra-wide range of temperature[J].Journal of Hunan University,1993,20(6):34-38(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 靳宝安,袁桃利,贾玉霞.晶振温补网络研究[J].陕西科技大学学报,2005,23(3):81-85. Jin B A,Yuan T L,Jia Y X.Analyse and research on the temperature compensate net of crystal oscillator[J].Journal of Shaanxi University of Science & Technology,2005,23(3):81-85(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 邓敏,陈卫.宽温高稳定度的温度补偿技术[J].电讯技术,2008,48(6):44-46. Deng M,Chen W.Temperature compensation technology with wide temperature and high frequency stability[J].Telecommunication Engineering,2008,48(6):44-46(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [6] | 李建文,祖兵.高准确度宽温石英晶振热敏网络温度补偿[J].传感器技术,2004,23(5):68-71. Li J W,Zu B.Temperature compensation to quartz crystal oscillator by thermistor net with high accuracy within wide temperature scope[J].Journal of Transducer Technology,2004,23(5):68-71(in Chinese). |
| Cited By in Cnki (14) | Click to display the text | |
| [7] | 黄显核.最佳逼近法在晶体频温曲线拟合和TCXO中的应用[J].压电与声光,2005,27(4):452-454. Huang X H.Application of the best approximation algorithms on frequency-temperature curve fit and TCXO[J].Piezoelectrics and Acoustooptics,2005,27(4):452-454(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [8] | Mi Z,Wei X C.A 0.1 ppm successive approximation frequency-temperature compensation method for temperature compensated crystal oscillators (TCXO)[C]//Proceedings of 2009 World Congress on Computer Science and Information Engineering.Piscataway,NJ:IEEE Press,2009:493-498. |
| [9] | Wei F,Xian H H,Feng T,et al.An improved microcontroller compensated low phase noise overtone TCXO[C]//Proceedings of 2009 IEEE International Frequency Control Symposium and the 22nd European Frequency and Time forum. Piscataway,NJ:IEEE Press,2009:974-977. |
| [10] | 孙敏,黎敏强,陈中平,等.一种宽温高精度温补晶振的研制[J].电子技术,2013,26(8):90-92. Sun M,Li M Q,Chen Z P,et al.A high precision temperature compensated crystal oscillator in wide temperature range[J].Electronic Science and Technology,2013,26(8):90-92(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [11] | 江玉洁,陈辰,伏全海,等.一种全集成化的温补晶体振荡器[J].宇航计测技术,2003,23(3):52-57. Jiang Y J,Chen C,Fu Q H,et al.A full-integrated temperature compensated crystal oscillator[J].Journal of Astronautic Metrology and Measurement,2003,23(3):52-57(in Chinese). |
| Cited By in Cnki (11) | Click to display the text | |
| [12] | 尹红斌.基于模拟-数字相结合的新型温补晶振的产业化设计[D].西安:西安电子科技大学,2007. Yin H B.Industrialized research of temperature compensated crystal based on analog-digital method[D].Xi'an:Xi'an Eletronic Science and Technology University,2007(in Chinese). |
| [13] | 王艳,黄显核,阎立群,等.高精度低噪声集成温度补偿晶体振荡器[J].压电与声光,2010,32(6):909-911. Wang Y,Huang X H,Yan L Q,et al.An integrated temperature compensated crystal oscillator with high-precision and low-noise[J].Piezoelectrics and Acoustooptics,2010,32(6):909-911(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [14] | Asad A A.Phase noise and jitter in CMOS ring oscillators[J].IEEE Journal of Solid-State Circuits,2006,41(8):1803-1816. |
| Click browse the original | |
| [15] | Behzad R.A study of phase noise in CMOS oscillators[J].IEEE Journal of Solid-State Circuits,1996,31(3):331-343. |
| Click browse the original | |
| [16] | 韩艳菊,杨科,郑鸿耀.一种用于模拟温度补偿晶体振荡器的温度补偿方法:中国,201310739925.3[P].2013-12-30. Han Y J,Yang K,Zheng H Y.A temperature compensation method for analog temperature compensated crystal oscillator:China,201310739925.3[P].2013-12-30(in Chinese). |
| [17] | 赵声衡,赵英.晶体振荡器[M].北京:科学出版社,2008:316-322. Zhao S H,Zhao Y.Crystal oscillator[M].Beijing:Science Press,2008:316-322(in Chinese). |
| [18] | 孙艳丰,郑加齐,王德兴,等.基于遗传算法的约束优化方法评述[J].北方交通大学学报,2000,24(6):14-19. Sun Y F,Zheng J Q,Wang D X,et al.A survey of constraint optimization method based on genetic algorithm[J].Journal of Northern Jiaotong University,2000,24(6):14-19(in Chinese). |
| Cited By in Cnki (71) | Click to display the text | |
| [19] | 吕善伟,韩艳菊,王伟.遗传算法综合阵列的幅度和相位方向图[J].北京航空航天大学学报,2005,31(9):1014-1017. Lü S W,Han Y J,Wang W.Synthesis of the array's amplitude and phase pattern using genetic algorithm[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(9):1014-1017(in Chinese). |
| Cited By in Cnki (18) | Click to display the text |
