广泛用于汽车、高速列车、舰船以及航空航天飞行器外壳结构的板壳结构正面临着由质量轻、刚度大、抗冲击性能好的结构需求所带来的越来越严酷的振动噪声问题的挑战.另一方面,智能材料科学与技术的发展为解决工程中的难题开辟了新的思路.自1956年Olsen提出可以将压电材料用于结构的振动、噪声控制之后^[1],该领域的研究得到了迅猛发展.Hagood和von Flotow探索了应用压电分支电路对结构振动进行被动控制的可能性^[2],紧接着研究人员对分支电路的设计进行了更为深入的探索^{[3, 4, 5]}.为实现对结构的多阶共振抑制,Hollkamp采取了在分支电路中并联谐振电路的方法^[6],Park C H和Park H C在分支电路中添加了负电容^[7],刘莹等采用了压电阻塞电流分支电路^[8],李琳和刘学则将“选通电路”的思想引入了分支电路^[9].Dell’Isola等提出了压电网络的概念并将其应用于梁、板类结构,发现其同样具有多模态振动控制效果,并且结构简单,能在被动控制的基础上降低对电学元件的要求,同时还不需要引入选通电路,也不需要考虑压电片的设置位置^{[10, 11, 12, 13]}.易凯军和李琳在研究四边简支压电网络板机电耦合动力学特性的基础上,分析了其振动控制的原理和效果^{[14, 15]}.然而,在工程应用中,板的固定方式更接近固支.而固支条件下薄板横向自由振动问题的振型函数封闭解的获得比简支板要困难得多,这在很大程度上限制了对压电网络板振动控制研究的深入.Xing和Liu^[16]采用分离变量法求解了在Hamilton体系下的薄板横向自由振动的特征值问题,得到了简支和固支任意组合边界条件下的振型函数精确解.本文在此基础上引入压电网络,求解了具有压电网络的四边固支板(四边固支压电网络板)的机电耦合动力学方程,进而研究了压电网络用于对四边固支板多阶共振的抑制作用.为今后将其应用于工程实际以及开展实验研究提供理论基础和设计指导.
1 压电网络板的机电耦合动力学方程本文基于文献^[15]提出的压电网络板模型进行分析,该模型包含压电复合板以及电路网络两部分.图 1为压电网络板的示意图,其中压电片在板上呈周期性分布,各压电片之间通过相同的电路连接.从图 1可以看出,压电网络板是一个周期结构,压电复合板的一个结构单元(又称元胞)如图 2所示.

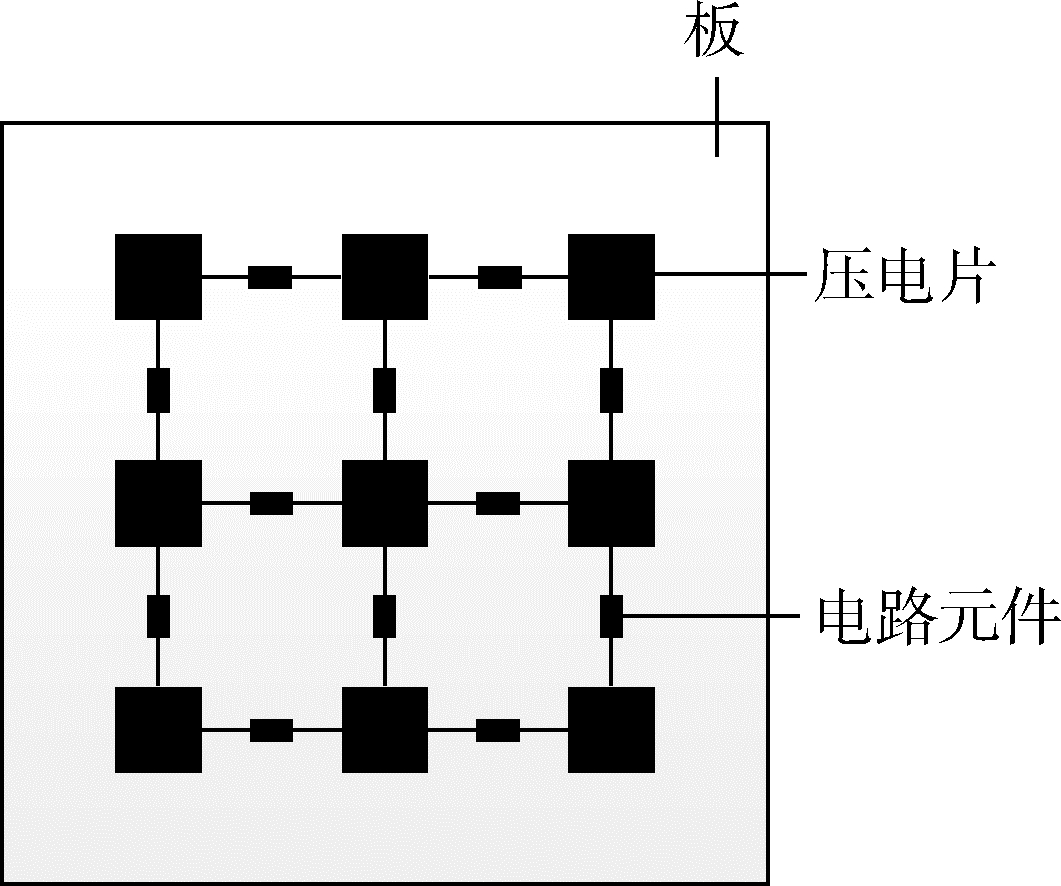图 1 压电网络板Fig. 1 Piezo electro mechanical-plate

图选项

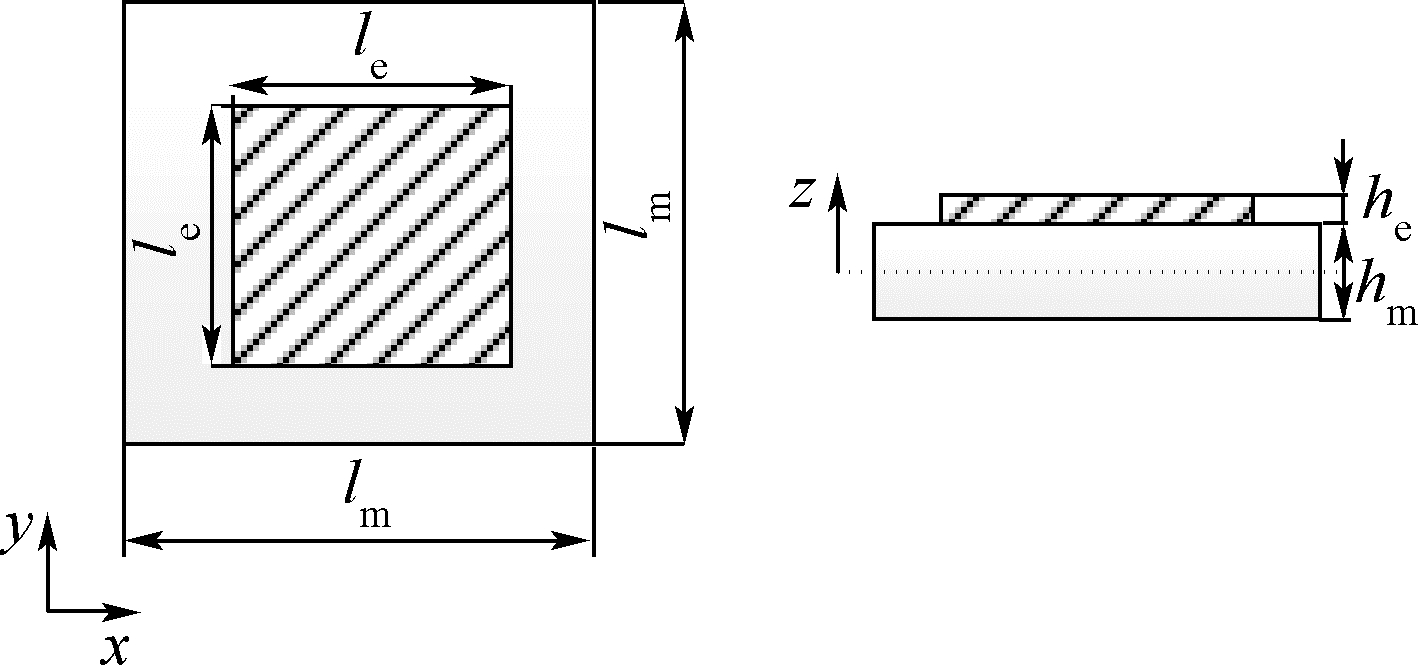x,y,z—板的坐标轴;le,lm—压电片长和板长; he,hm—压电片高和板高.图 2 压电复合板元胞Fig. 2 Cell of piezoelectric composite plate

图选项

压电片(PZT)之间可以通过不同形式的电路相连接,其连接方式如图 3所示.其中:图 3(a)表示元胞之间通过并联的电感L和电阻R相连接,称之为电感电阻并联型压电网络板(LR-PEM).图 3(b)为电阻型压电网络板(R-PEM)的电路形式,即元胞之间仅通过电阻R相连.

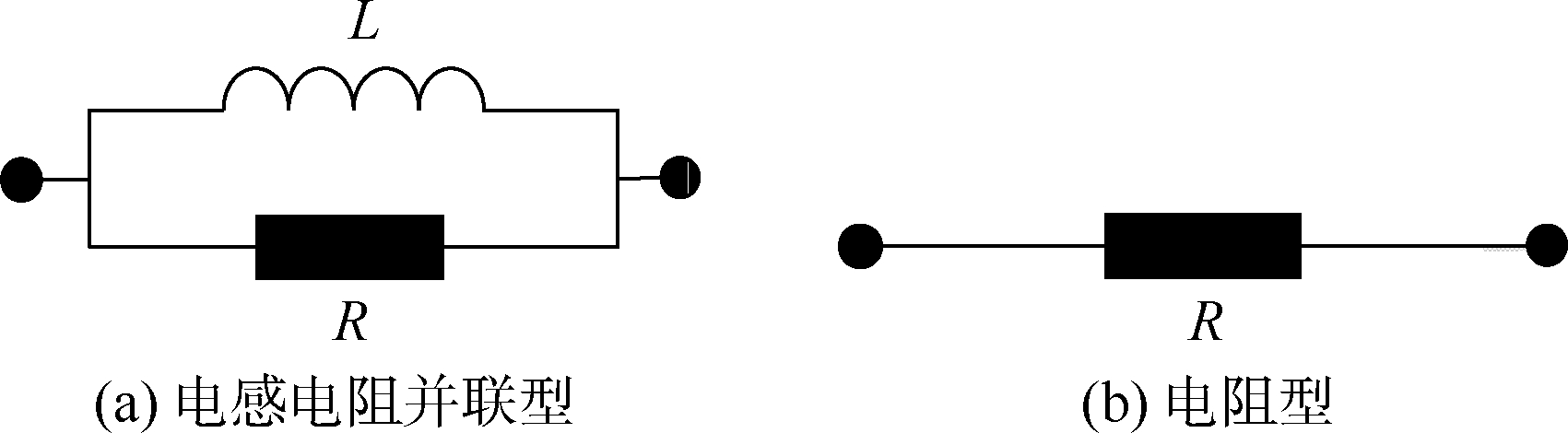图 3 压电片之间的电路连接方式Fig. 3 Circuit between two different PZTs

图选项

该压电网络板的无量纲机电耦合动力学方程组^[15]为
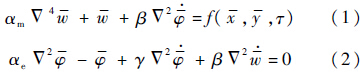
式中:α_m和α_e分别为机械系数和电学系数;$\bar w$和$\bar \varphi $分别为板横向振动位移和板表面的磁通量;τ为无量纲时间;β和γ分别为耦合系数和综合电学参数;$\bar x$和$\bar y$为无量纲化的板的x和y坐标.这些参数定义为

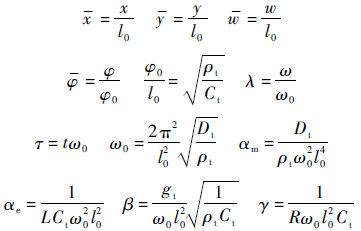
其中:w为压电复合板的法向位移;φ为压电复合板表面的磁通量;φ₀为特征磁通量；l₀为特征长度(板长);ω₀为特征频率;C_t、D_t和ρ_t分别为均匀化板的压电片电容、抗弯刚度和密度.
其他参数的表达式分别为

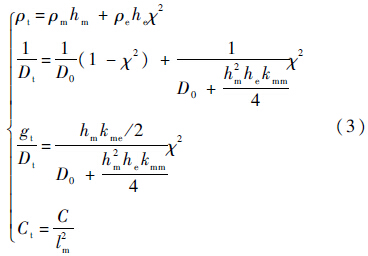
式中:${D_0} = \frac{{{E_m}h_m^3}}{{12\left( {1 - \mu _m^2} \right)}}$为板抗弯刚度;${k_{mm}} = \frac{{{E_e}}}{{1 - \mu _e^2}}$和${k_{me}} = \frac{{{d_{31}}{E_e}}}{{1 - {\mu _e}}}$为弹性矩阵系数;χ=l_e/l_m;E_m、E_e,μ_m、μ_e,ρ_m、ρ_e分别为板(带下标m)和压电片(带下标e)的弹性模量、泊松比和密度;C为压电片的电容;d₃₁为压电材料的机电耦合常数.本文的材料参数及模型几何尺寸由文献^[14]确定.
2 四边固支压电网络板动力学方程的求解2.1 压电网络板对简谐激励的响应解压电网络板的受迫振动响应求解取决于板的边界条件,四边固支压电网络板的边界条件为:在$\bar x$=0和$\bar x$=1处,
在$\bar y$=0和$\bar y$=1处,
为求解压电网络板动力学方程组(方程(1)和方程(2)),设:
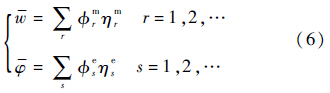
式中:$\phi $_r^m为四边固支板的振型函数,即当方程(1)中β=0、f=0时的特征解,其对应的特征值为λ_r^m；η_r^m为该模态空间的广义坐标;$\phi $_s^e为方程(2)中β=0、γ=0时的特征解,代表电路网络的特征函数,其对应的特征值为λ_s^e；η_s^e为该模态空间的广义坐标,r和s为阶数.
根据特征解的性质,易知:
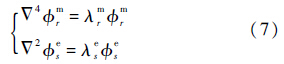
式中：
对应的特征值为
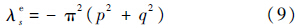
式中:p和q分别为振型函数在x方向和y方向的半波数.$\phi $_r^m和λ_r^m可以由文献^[16]提出的方法确定.将式(6)和式(7)代入方程(1)和方程(2)中,可得
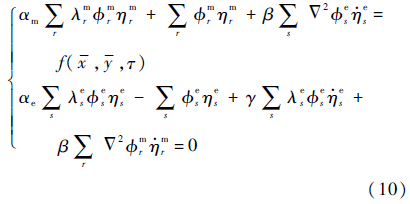
利用特征函数$\phi $_r^m以及$\phi $_s^e各自的正交性,式(10)可以写成
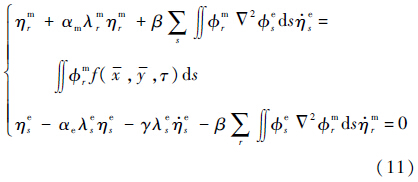
令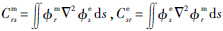，式(11)还可以写为式(12)的矩阵形式(为避免电路短路时系统的共振响应出现无穷大,式中增加了粘滞阻尼系数ξ_v):
式中：
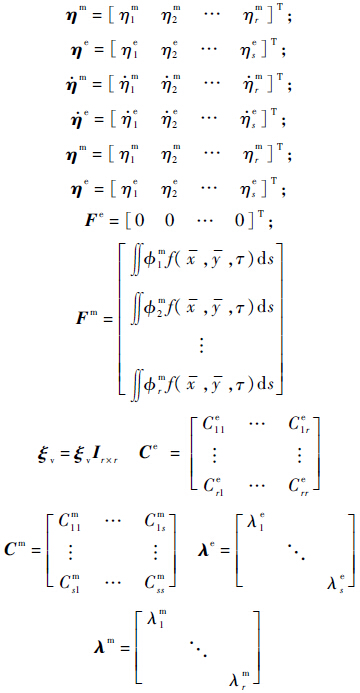
由C_rs^m构成的矩阵称之为机电耦合矩阵,矩阵中的每个元素都标志着第r阶结构振动模态和第s阶压电网络模态的耦合程度,该元素的绝对值越大,表明对应的机电模态耦合程度越强,机电能量的转化能力就越强.
线性系统(式(12))对简谐激励的响应的表达式为

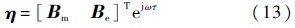
式中：
则在简谐激励下压电网络板的位移表达式(6)为
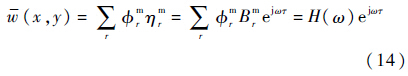
式中:H(w)为随激振力频率变化的位移空间分布规律表达式.
在式(14)的基础上,可以分析压电网络对结构的多阶共振抑制效果.
在进行谐响应分析时,本文采取单点激励的方式,如图 4所示.

图 4 激励方式示意图Fig. 4 Excitation pattern schematic

图选项

对于式(6)中的$\phi $_s^e和$\phi $_r^m,本文将各取前10阶模态作为对应空间的基底.
2.2 四边固支压电网络板的模态特性四边固支板横向自由振动的振型函数表达式已由文献^[16]给出.据此,式(6)中的$\phi $_r^m可表示为
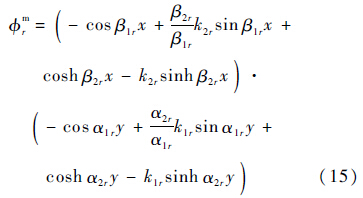
式中:
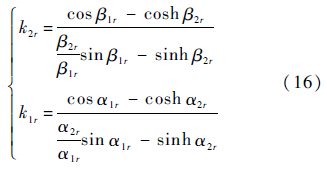
其中:β_1r、β_2r、α_1r、α_2r、k_1r和k_2r为待定系数.
特征方程组为
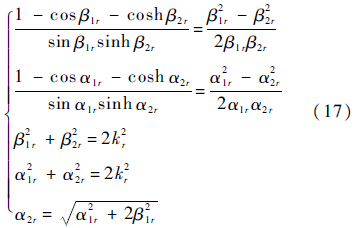
式中：λ_r^m=k_r⁴=ω_r²/α_m为板横向振动特征值，ω_r为板横向振动固有频率.
通过对式(17)的求解,可以得到四边固支板的各阶固有频率及振型函数.表 1列出了四边固支压电网络板的前10阶无量纲固有频率及振型半波数,半波数代表了振型在空间的分布规律.如第4阶振型的半波数为2/2,代表该阶振型在x方向有2个半波,y方向有2个半波.图 5为四边固支板的前4阶振型.
表 1 四边固支压电网络板无量纲固有频率及半波数Table 1 Eigenvalues and half wave numbers of clamped piezo electro mechanical-plate

阶数	1	2	3	4	5
频率	1.8	3.7	3.7	5.4	6.7
半波数	1/1	1/2	2/1	2/2	1/3
阶数	6	7	8	9	10
频率	6.7	8.3	8.3	10.7	10.7
半波数	3/1	2/3	3/2	1/4	4/1

表选项

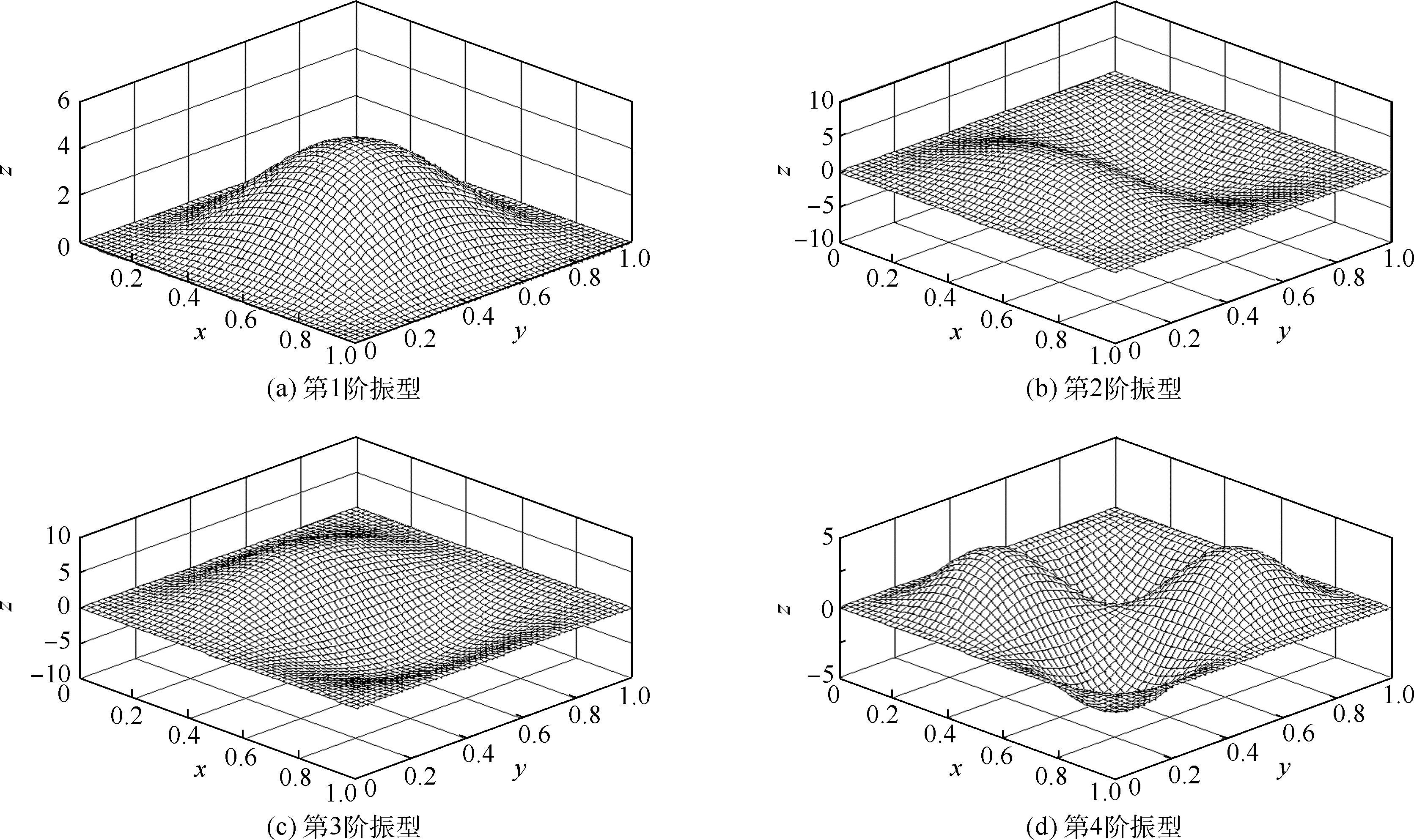图 5 四边固支板前4阶振型Fig. 5 First four mode shapes of clamped plate

图选项

本文的分析模型为正方形板,存在重频的振型,比如第2、3阶,第5、6阶,第7、8阶,第9、10阶,因此在前10阶模态中只有6阶不同的固有频率,本文后面提到的共振阶数均指的是频率的阶数.对于重频点,其共振响应的振型图为两个重频振型的线性组合.
3 压电网络对四边固支板的多阶共振抑制效果3.1 电阻型电路的多阶共振抑制作用分析为避开各阶振型的节线位置,更好地观察共振抑制效果,首先在正方形板上选取x=0.4,y=0.3这一点进行拾振分析,同时以前4阶共振为例说明四边固支压电网络板的多阶共振抑制效果.
对于R-PEM,当电阻值很小或者很大时,电路中耗散的能量均较少,因此每一阶共振都存在一个最优电阻值R_opt,使得此时电路耗散的能量最多,共振抑制效果最好.图 6为电阻对共振峰值的影响.图 6(a)~图 6(d)依次为电阻对前4阶共振响应峰值的影响,可以看出每一阶共振均对应一个最优电阻.

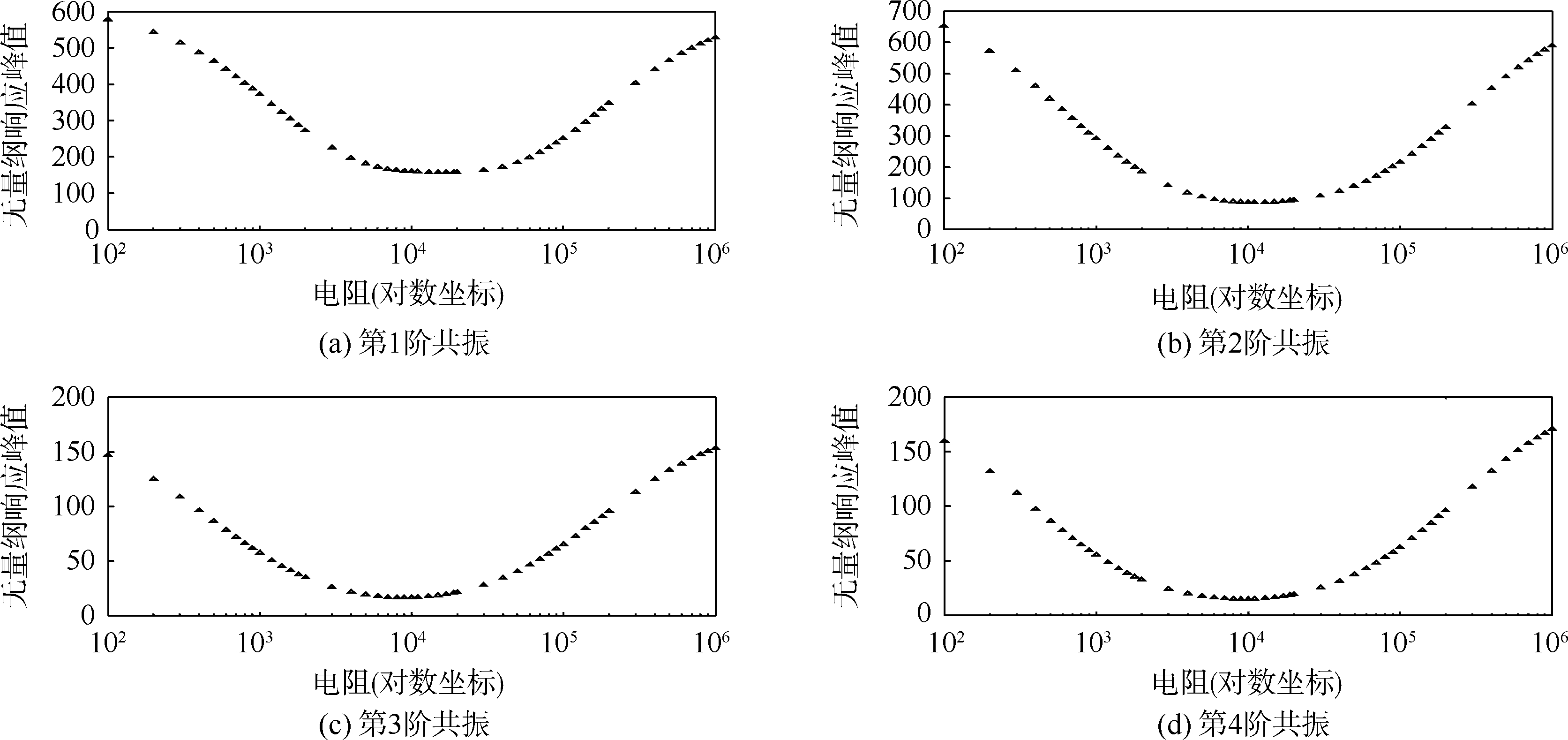图 6 电阻对共振峰值的影响(R-PEM)Fig. 6 Influence of resistance on resonance peak value (R-PEM)

图选项

为进一步分析电阻对结构共振的抑制效果,定义敏感因子δ=(Δw/w_min)/(ΔR/R_opt),式中:w_min为对应最优电阻值R_opt的拾振点位移共振峰值;ΔR和Δw分别为电阻的改变量以及由此引起的位移共振峰值的改变量.显然,δ越小说明板的位移响应峰值对最优电阻的变化不敏感,也就是说在一个较大的电阻区间,都可以有较好的共振抑制效果.
表 2给出了对应Δw=5%w_min的最优电阻改变区间以及各阶共振峰值对电阻的敏感度.从中可以看出,虽然各阶最优电阻不同,但是由于各阶的w_min均对电阻不太敏感,即最优电阻区间较宽,因此可以选取这些最优电阻区间的交集作为全局最优电阻区间.
表 2 各阶共振峰值对电阻的敏感度Table 2 Sensitivity of resonance to resistance peak value

阶数	最优电阻/Ω	最优区间/Ω	敏感因子
第1阶	15000	7300~32600	0.03
第2阶	11000	7400~17400	0.06
第3阶	8900	6500~12500	0.07
第4阶	9100	6700~12700	0.08

表选项


图 7为电阻取8900Ω时,R-PEM的幅频特性曲线.从图中可以看出,电阻型电路对结构的前4阶共振均具有较好的抑制效果,即R-PEM具有多模态振动抑制功能.

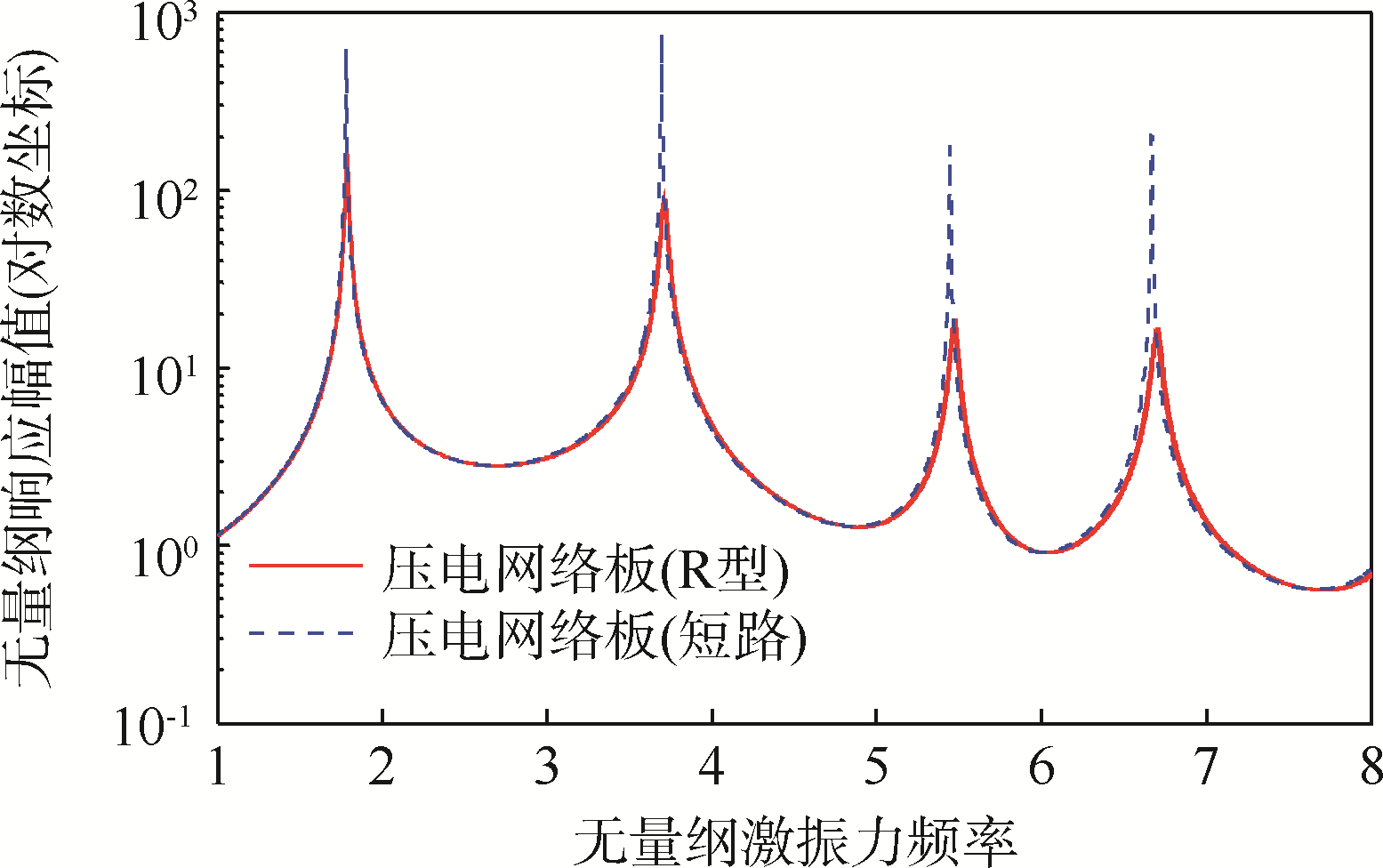图 7 R-PEM振动控制效果Fig. 7 Vibration control effect of R-PEM

图选项

上述分析基于某一确定点的响应,为了研究所得结论的普适性,下面以各阶(前4阶)共振响应极值点作为分析点,分别计算这些点的最优电学参数,在此基础上分析其对整个板的多阶共振抑制效果,本部分仍采用图 4所示的单点激励方式.通过对压电网络板短路时前4阶共振响应幅值的计算可以发现,前4阶共振响应极值点的个数分别是1、2、4以及4.
表 3显示了前4阶共振响应极值点对应的最优电阻值,其中极值点1至极值点4不代表具体的点,而是表示极值点的序号,不同阶的极值点位置也不相同.结合表 1可以看出,对于电阻型压电网络板,同一阶不同点计算出的最优电阻值相差不大,不同阶的最优电阻值不相同.下面将以第1阶最优电阻为例,说明R-PEM最优电阻对结构多阶共振的抑制效果.图 8为R-PEM振动抑制效果云图.图 8(a)~图 8(d)分别为当系统取第1阶最优电阻时,压电网络板上各点前4阶共振响应幅值与压电网络板短路时相比降低值(共振幅值降低值)的云图.从图 8中可以清楚地看出,由于降低值均为非负值,所以对于整个结构来说,R-PEM均具有多阶共振抑制效果.
表 3 共振响应极值点最优电阻Table 3 Optimal resistance to extreme point of resonance response

Ω
电阻	第1阶	第2阶	第3阶	第4阶
极值点1电阻	15200	11000	9000	9200
极值点2电阻		11000	8900	9100
极值点3电阻			9000	9300
极值点4电阻			8900	9300

表选项

图 8 R-PEM振动抑制效果云图Fig. 8 Contours of vibration suppression effect of R-PEM

图选项

3.2 电感电阻并联型电路的多阶共振抑制作用分析LR-PEM的电路中采用了电感和电阻两种电学元件.
图 9为LR-PEM的电感及电阻对共振峰值的影响.图 9(a)~图 9(d)分别为LR-PEM的电学参数对前4阶共振响应幅值的影响,从中可以发现对应每一阶共振存在不止一个最优电学参数(对应曲面谷值).图 9(a)的曲面具有2个极值点;图 9(b)的曲面具有3个极值点;图 9(c)和图 9(d)的曲面均只有1个极值点.

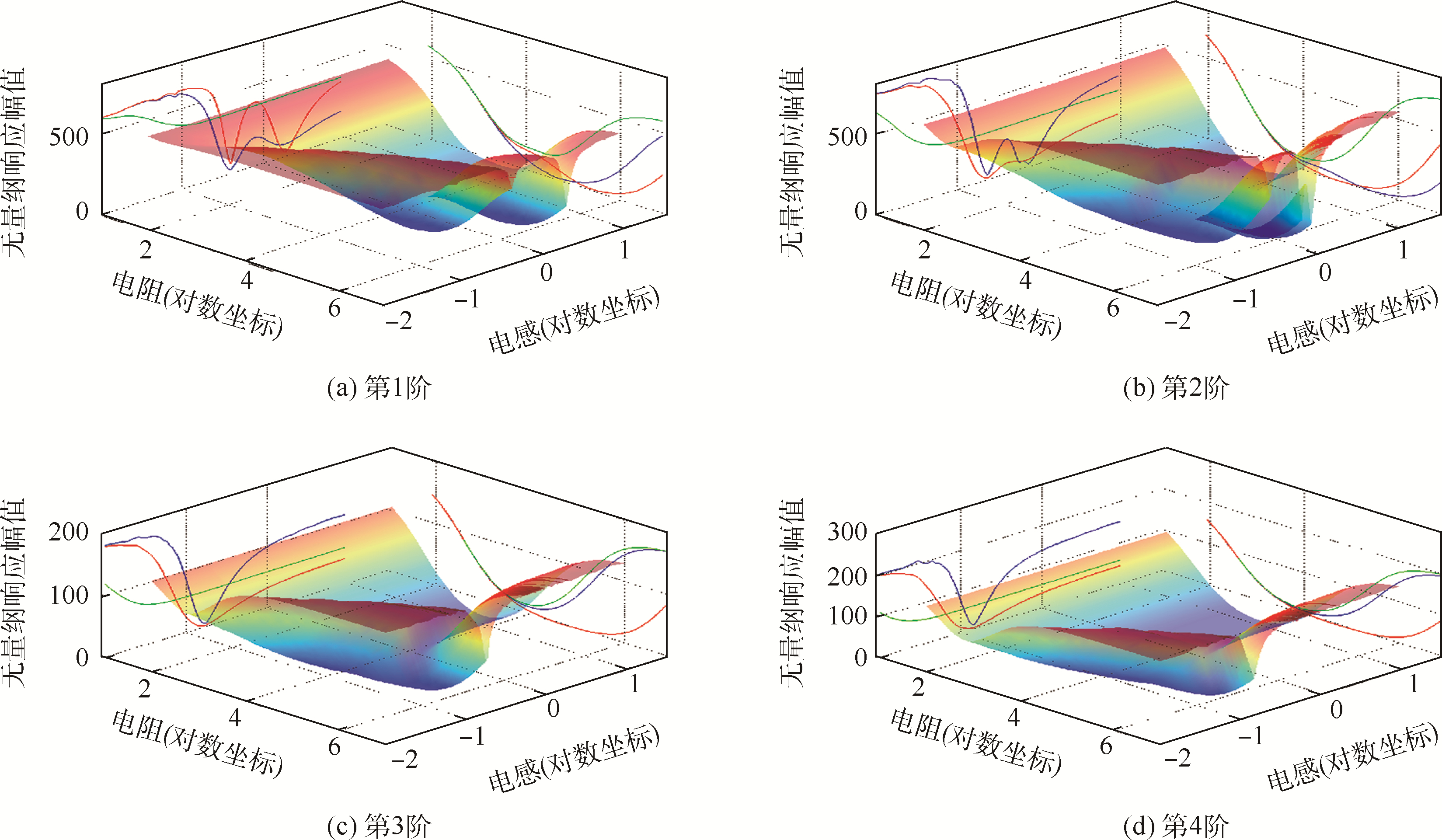图 9 电感及电阻对共振峰值的影响(LR-PEM)Fig. 9 Influence of inductance and resistance on resonance peak value (LR-PEM)

图选项

表 4为各阶共振对应的所有局部最优电学参数.下面以第2阶共振为例,从能量耗散的角度分析其存在多组局部最优电学参数的机理.根据其最优电感从小到大排列,将对应第2阶共振的3组局部最优电学参数依次记作A、B和C.
表 4 各阶共振对应的最优电学参数Table 4 Optimal electrical parameters to resonance among different orders

阶数	极值点电感/mH	极值点电阻/Ω	极值点幅值
第1阶	413	60100	20.5
	2005	293300	20.3
第2阶	241.7	60100	10.3
	608	579000	30.2
	785.6	307900	14.5
第3阶	180.3	56900	1.6
第4阶	147.6	60200	1.4

表选项


图 10为各阶电路系统耗能对比.图 10(a)~图 10(c)显示了在压电网络板的第2阶共振频率范围内,不同局部最优电学参数下各阶电路能量消耗的分布情况,各阶电路消耗的能量表达式记为E^R-damp=-0.5γλ_i^e(B_i^e)²,其中：i=1,2,…,γ为电路中的电阻,B_i^e为各阶电路模态对应的特征值,λ_i^e为各阶电路响应的广义坐标幅值.由于正方形板存在重频现象,所以每一阶电路的耗能是由同一阶固有频率对应的各个电路模态耗能叠加起来的,比如说第5阶电路耗能则是第7阶和第8阶压电网络模态耗能的总和.
从图 10中可以看出,这3组最优电学参数分别使压电网络系统的第2阶、第5阶以及第6阶电路承担了大部分消耗结构振动能量的工作,换句话说,合理地选取电学参数可使结构系统中第2阶振动能量通过不同的电路通道进行耗散,进而达到减振的效果.

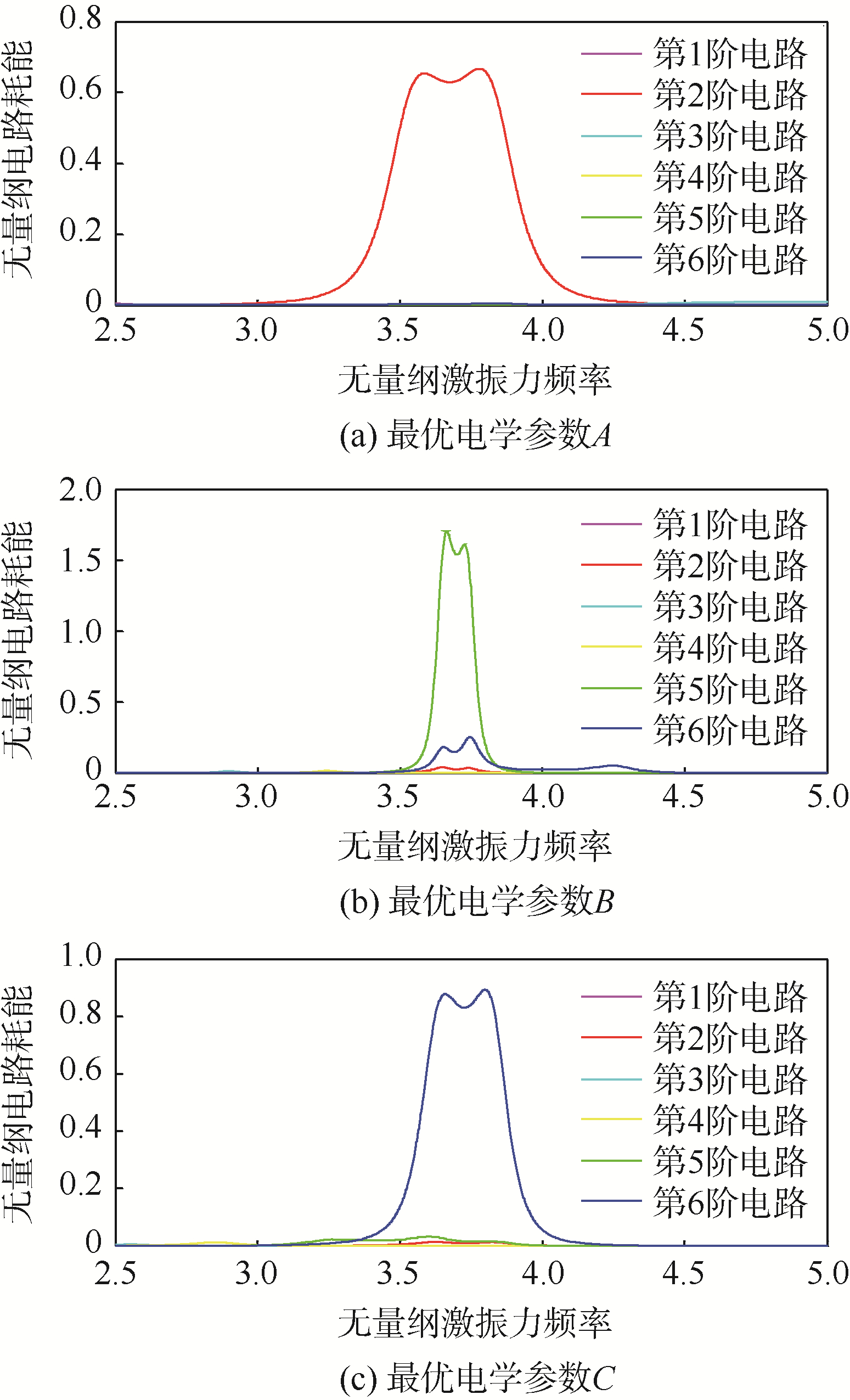图 10 各阶电路系统耗能对比Fig. 10 Comparison of energy dissipation in electrical system among different orders

图选项

图 11展现了四边固支压电网络板机电耦合矩阵各元素的相对大小,其中横坐标代表前10阶压电网络电路模态,纵坐标代表前10阶结构振动模态,每一个小方块的颜色冷暖程度代表了不同阶次机电耦合系数的大小.与四边简支压电网络板只有对角线元素非零不同,四边固支板还在不同阶次的结构振动模态和压电网络电路模态之间存在耦合.

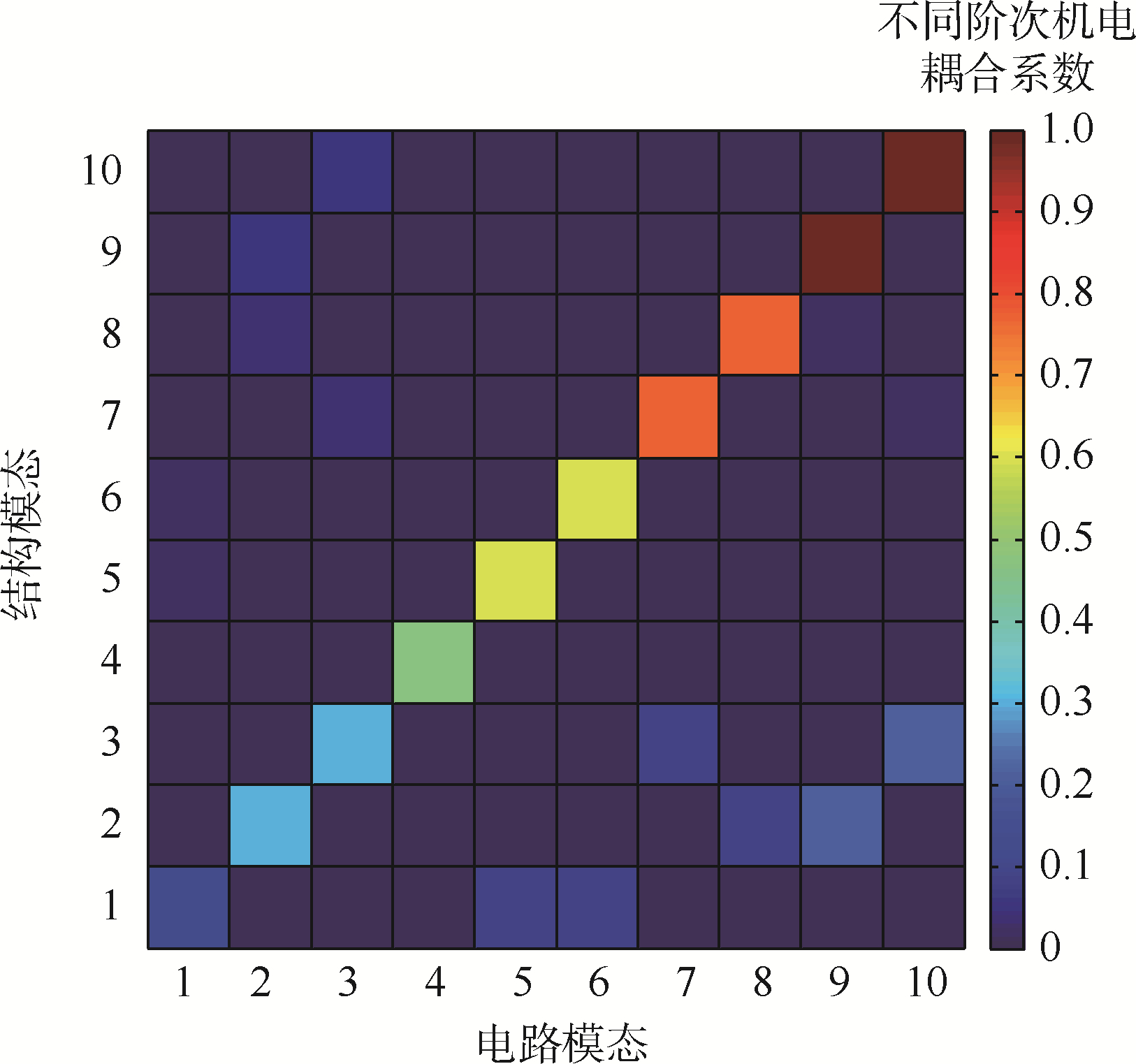图 11 机电耦合矩阵Fig. 11 Electro-mechanical coupling matrix

图选项

从图 11中可以看出,第2阶结构的振动模态恰好和第2阶、第8阶以及第9阶电路模态存在耦合.由于正方形板存在重频现象,所以结构和电路均只有6阶固有频率.也就是说,第8阶和第9阶电路模态分别对应第5阶和第6阶电路固有频率.换句话说,第2阶结构固有频率下的机械振动分别与第2阶、第5阶和第6阶电路固有频率下的压电网络存在耦合.并且其机电耦合系数是第2阶最大,第5阶最小.这也对应着局部最优电学参数A的共振抑制效果最好,B的共振抑制效果最差.
结合表 3还可以看出,耦合的电路阶次越高,其需要的电感也越高,换句话说,对于高阶振动,如果其与低阶次的电路模态存在耦合,其对应的电感值就越低,而低电感在工程上更容易实现,因此对于结构的高阶共振,可以选择与低阶电路耦合对应的局部最优电学参数以进一步降低电感值.
由此得出结论,对于四边固支的LR-PEM来说,各阶共振存在多个局部最优电学参数的机理在于其结构振动模态和多阶电路模态存在耦合,并且耦合值越高,其对应的共振抑制效果就越好.不同的最优电学参数的选取意味着使该阶共振与不同电路模态的耦合达到最大.
在以下的分析中,称结构和电路同阶模态对应的最优电学参数为主最优电学参数,非同阶模态对应的最优电学参数称为次最优电学参数.分析表明,主最优电学参数对其他阶的共振抑制效果明显强于次最优电学参数.因此本文后面的分析均取各阶的主最优电学参数作为LR-PEM的最优电学参数.
根据第3.1节关于敏感因子的定义,表 5显示了当Δw=5%w_min时,LR-PEM各阶最优电学参数的敏感因子.从中可以看出,相对电阻来说,共振峰值对电感更加敏感,并且各阶最优电感会随着共振频率的增加而降低.
表 5 各阶最优电学参数的敏感性Table 5 Sensitivity of optimal elecrical parameters of different orders

最优电学参数及 其敏感性	第1阶	第2阶	第3阶	第4阶
最优电阻/Ω	60100	60100	56900	60200
电阻敏感因子	0.1	0.1	0.1	0.1
最优电感/mH	413	241.7	180.3	147.6
电感敏感因子	3.8	3.2	2.3	2.7

表选项


图 12为LR-PEM振动控制效果.图 12(a)~图 12(d)分别显示了不同阶最优电学参数控制下的压电网络板幅频特性曲线.从中可以看出，LR-PEM同样具有多阶共振抑制效果,但是设计点的共振抑制效果明显要比其他阶更好,这是因为电感可以调节电路模态的固有频率,在设计点的最优电学参数下,对应阶数的电路模态固有频率与结构振动固有频率最匹配,使得二者之间的机电转换效率最高,结构振动能量会很快转换到电路中消耗掉,进而降低响应幅值,而其他阶电路和结构模态由于频率匹配程度较差,机电转换效率较低,因而振动控制效果较差.

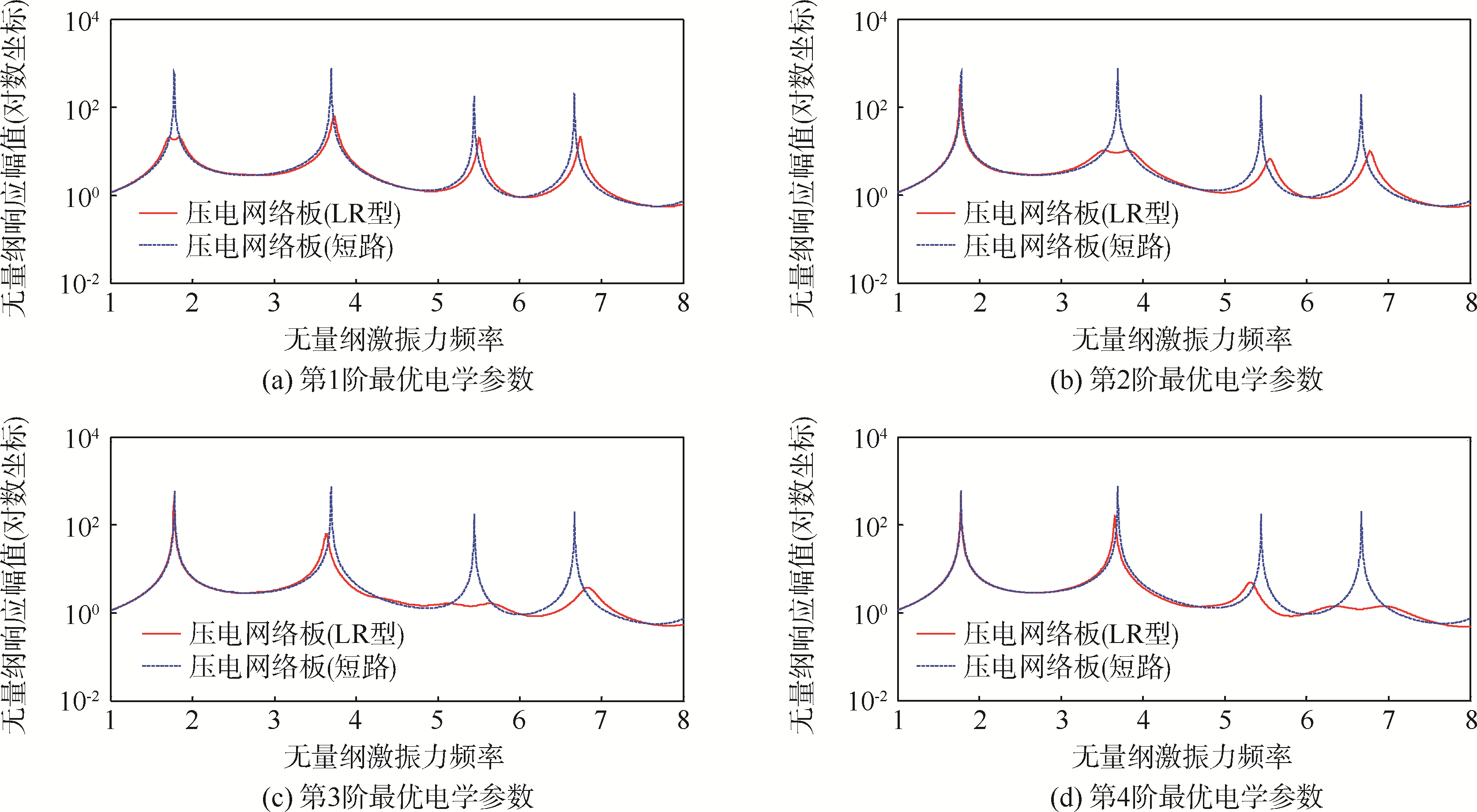图 12 LR-PEM振动控制效果Fig. 12 Vibration control effectiveness of LR-PEM

图选项

同样为了研究所得结论的普适性,分析整个板的多阶共振抑制效果,这里沿用R-PEM在该部分的分析方法.表 6显示了前4阶共振响应极值点对应的最优电学参数值,其中极值点1至极值点4代表的意义与表 2相同,将各个极值点计算出的平均值作为整个板的最优电学参数.结合表 5可以看出,对于LR-PEM,同一阶不同点计算出的最优电学参数值不相同,不同阶的最优电学参数也不同.
以第3阶最优电学参数为例,说明LR-PEM的最优电学参数对结构多阶共振的抑制效果.图 13为LR-PEM振动抑制效果云图.图 13(a)~图 13(d)分别为当电路取第3阶最优电学参数时,压电网络板上各点前4阶共振响应幅值与压电网络板短路时相比降低值的云图.从图 13中可以清楚地看出,由于降低值均为非负值,所以对于整个板来说,LR-PEM均具有多阶共振抑制效果.
表 6 共振响应极值点最优电阻和电感Table 6 Optimal resistance and inductance to extreme points of resonance response

最优电阻及电感		第1阶	第2阶	第3阶	第4阶
极值点1	电阻/Ω	60200	61600	56500	59500
	电感/mH	414.4	241.4	182.4	148.4
极值点2	电阻/Ω		61800	61800	62800
	电感/mH		240.8	179.9	146.4
极值点3	电阻/Ω			62100	60300
	电感/mH			174.7	150.1
极值点4	电阻/Ω			64000	61400
	电感/mH			173.5	145.5

表选项

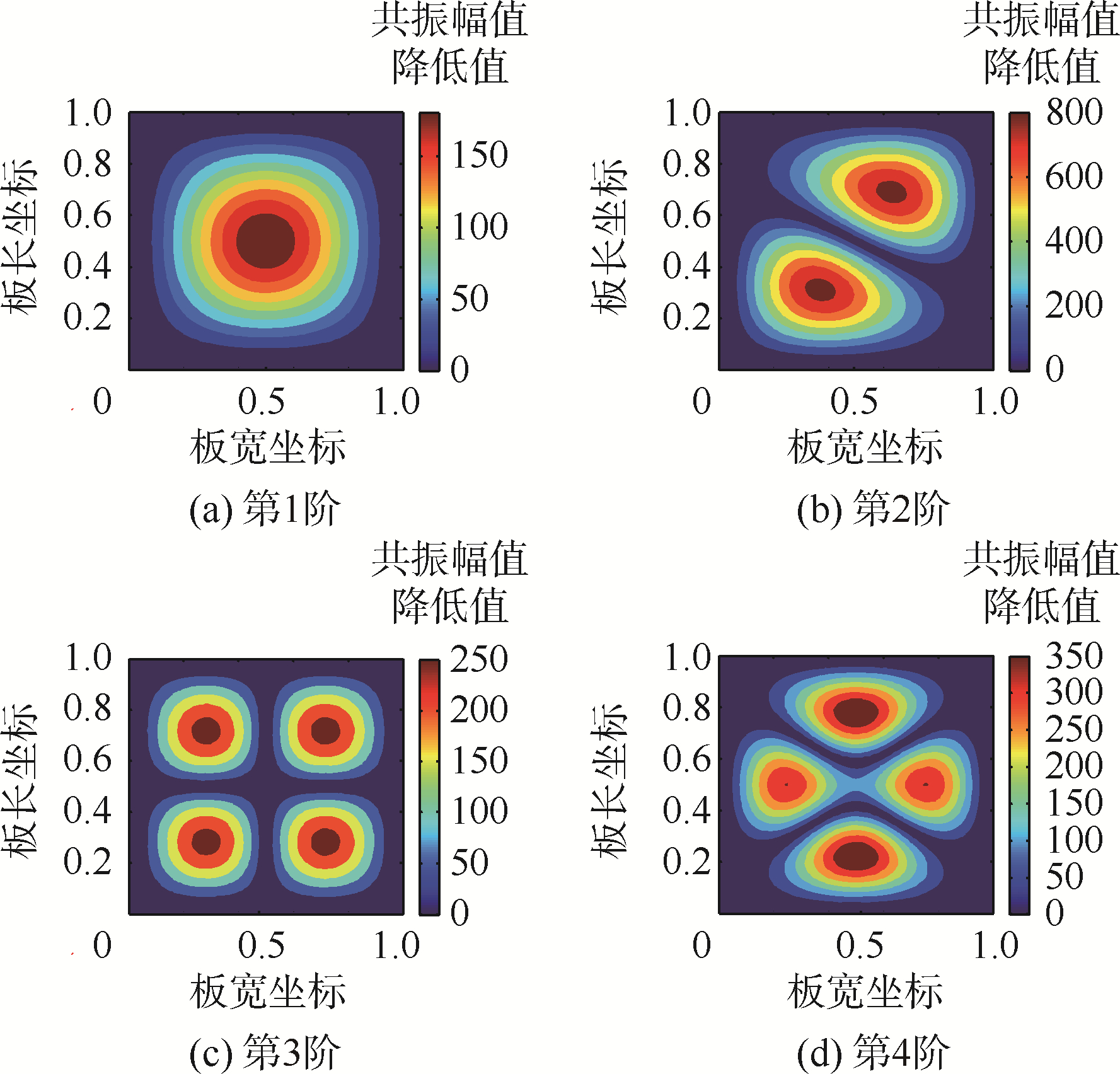图 13 LR-PEM振动抑制效果云图Fig. 13 Contour of vibration suppression effect (LR-PEM)

图选项

3.3 R-PEM与LR-PEM多阶共振抑制效果对比图 14为各类最优电学参数对共振峰值的影响.图 14(a)~图 14(d)依次为LR-PEM的各阶最优电学参数对前4阶共振的抑制效果,并与R-PEM以及当各电路短路时的压电网络板进行了比较.从中可以看出,R-PEM与LR-PEM均可以对各阶共振进行有效抑制.对于设计频率点,LR-PEM可以达到比R-PEM更好的振动抑制效果,但是对于远离设计频率点的共振来说,LR-PEM的振动控制效果可能会比R-PEM还差,并且距离设计频率越远,LR-PEM的控制效果越差.

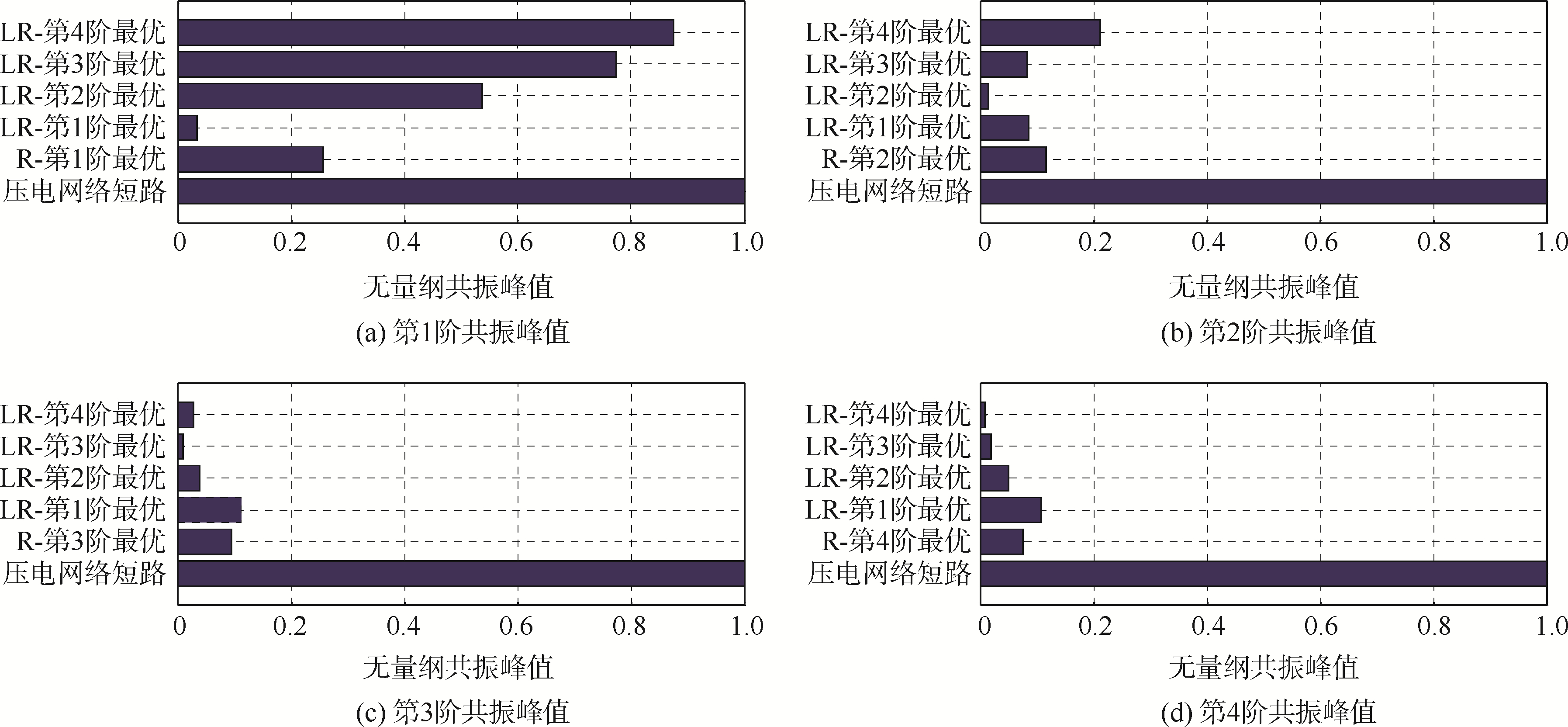图 14 各类最优电学参数对共振峰值的影响的比较Fig. 14 Comparison among influence of optimal circuit parameters on resonance peak value

图选项

4 结 论本文以四边固支板横向自由振动的解函数为模态坐标,求解了压电网络板的机电耦合动力学方程,得到了其在简谐激励下的频响函数表达式,并在此基础上分析了四边固支压电网络板的多阶共振抑制效果.该求解方法还可以推广至其他边界条件的情况.对于四边固支压电网络板,本文主要得到:
1) R-PEM和LR-PEM对整个压电网络板均具有多阶共振抑制效果.LR-PEM在设计频率点附近比R-PEM的共振抑制效果要好,但是对于远离设计频率点的共振来说,其控制效果会变差,有时甚至没有R-PEM的效果好.
2) R-PEM各阶最优电阻与共振频率有关,但是其控制效果对电阻不敏感,根据实际工程的需要,可以找到一个全局最优电阻区间,使得该区间内的电阻对各阶模态均具有理想的共振抑制效果.
3) 与四边简支边界条件不同,四边固支的LR-PEM具有多组局部最优电学参数,每一组参数都对应着与结构具有较强耦合能力的某一阶电路模态,并且主要通过该阶电路消耗能量以达到共振抑制效果.对于结构和电路同阶耦合的最优电学参数来说,此时的最优电阻与共振频率有关,最优电感随共振频率增加而降低,与电阻相比,压电网络板的振动控制效果对电感更加敏感.
4) 对于LR-PEM,在抑制结构的高阶共振时,可以选择与低阶电路模态存在较强耦合的局部最优电学参数以进一步降低需要的电感值.
参考文献

[1]	Olson H F.Electronic control of noise, vibration and reverberation[J].Journal of the Acoustical Society of America, 1956, 28(5):972-976.
	Click to display the text
[2]	Hagood N W, von Flotow A.Damping of structural vibrations with piezoelectric materials and passive electrical networks[J].Journal of Sound and Vibration, 1991, 146(2):243-268.
	Click to display the text
[3]	Park C H, Inman D J.Enhanced piezoelectric shunt design[J].Shock and Vibration, 2003, 10(2):127-133.
	Click to display the text
[4]	de Marneffe B, Preumont A.Vibration damping with negative capacitance shunts:Theory and experiment[J].Smart Materials and Structures, 2008, 17(3):035015.
	Click to display the text
[5]	张付兴,阎绍泽.压电陶瓷片与多种电路机电耦合的阻尼特性[J].清华大学学报:自然科学版, 2005, 45(8):1040-1043. Zhang F X, Yan S Z.Damping characteristics of piezoceramics shunted by various types of electrical circuits[J].Journal of Tsinghua University:Science and Technology, 2005, 45(8):1040-1043(in Chinese).
	Cited By in Cnki (7)
[6]	Hollkamp J J.Multimodal passive vibration suppression with piezoelectric materials and resonant shunts[J].Journal of Intelligent Material Systems and Structures, 1994, 5(1):49-57.
	Click to display the text
[7]	Park C H, Park H C.Multiple-mode structural vibration control using negative capacitive shunt damping[J].Journal of Mechanical Science and Technology, 2003, 17(11):1650-1658.
	Click to display the text
[8]	刘莹,卜雄洙,庞俊恒.基于压电分支阻尼的多模态电路被动控制的研究和应用[J].南京理工大学学报:自然科学版, 2007, 31(3):300-303. Liu Y, Bu X Z, Pang J H.Study and application of passive control of multiple mode based on piezoelectric shunt damping[J].Journal of Nanjing University of Science and Technology:Natural Science, 2007, 31(3):300-303(in Chinese).
	Cited By in Cnki (4)
[9]	李琳,刘学.压电结构系统机电耦合的强化与多阶共振抑制[J].北京航空航天大学学报, 2014, 40(8):1011-1016. Li L, Liu X.Enhancement of electromechanical coupling for piezoelectric system and suppression of multimode vibration[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(8):1011-1016(in Chinese).
	Cited By in Cnki
[10]	Dell'Isola F, Porfiri M, Vidoli S.Piezoelectro mechanical(PEM) structures:Passive vibration control using distributed piezoelectric transducers[J].Comptes Rendus Mécanique, 2003, 331(1):69-76.
	Click to display the text
[11]	Batra R C, Dell'Isola F, Vidoli S, et al.Multimode vibration suppression with passive two-terminal distributed network incorporating piezoceramic transducers[J].International Journal of Solids and Structures, 2005, 42(11-12):3115-3132.
	Click to display the text
[12]	Dell'Isola F, Henneke E G, Porfiri M.Synthesis of electrical networks interconnecting PZT actuators to damp mechanical vibrations[J].International Journal of Applied Electromagnetics and Mechanics, 2001, 14(1-4):417-424.
	Click to display the text
[13]	Vidoli S, Dell'Isola F.Vibration control in plates by uniformly distributed PZT actuators interconnected via electric networks[J].European Journal of Mechanics, A/Solids, 2001, 20(3):435-456.
	Click to display the text
[14]	李琳,易凯军.压电网络板的机电耦合动力学特性[J].北京航空航天大学学报, 2014, 40(7):873-880. Li L, Yi K J.Electromechanical coupled dynamic characteristics of the plate with piezoelectric network[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7):873-880(in Chinese).
	Cited By in Cnki (1)
[15]	易凯军,李琳.压电网络板的振动控制原理与控制效果[J].北京航空航天大学学报, 2014, 40(11):1629-1636. Yi K J, Li L.Vibration-controlling principle and controlling effectiveness of piezo-electro-mechanical plate[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(11):1629-1636(in Chinese).
	Cited By in Cnki
[16]	Xing Y F, Liu B.New exact solutions for free vibrations of rectangular thin plates by symplectic dual method[J].Acta Mechanica Sinica, 2009, 25(2):265-270.
	Click to display the text