对于如何获得较精确的磁力模型参数,国内外****进行了大量的研究,主要包括2种途径:理论计算法和实验辨识法.理论计算法一般用于磁轴承的设计阶段,它根据理想的磁路模型或有限元模型,计算出磁力模型的电流刚度和位移刚度[5, 6, 7].为计算方便,磁路模型建立在一系列的假设基础上,如忽略导磁材料的磁阻及忽略漏磁等;而有限元模型网格划分不可能无限细,同时材料属性设置也是基于理想情况,因此理论计算得到的模型参数精度较差,通常只用于控制器的初步设计.实验辨识法通过实验获得测试数据,经过一定方式的处理得到磁力模型参数.文献[8]对磁力、转子位移和磁轴承电流进行测量,然后通过改进的LMS(Least Mean Square)算法在线辨识磁力模型参数;文献[9]采用磁力测量法和自由振荡法对磁力模型参数进行精确辨识;文献[10]提出了一种基于简谐运动的磁力参数辨识方法,与自由振荡法较为相似.基于磁力直接测量的辨识方法一方面其辨识精度取决于测力计的测量精度,另一方面受安装空间的限制,应用不便;而自由振荡法容易受系统固有频率的影响,需要避开系统的共振频率,对数据的差分运算也容易放大误差.文献[11]通过控制磁轴承定子的支承角度,利用转子的重力间接获得磁轴承的磁力.但是转子的支承角度难免存在误差,同时为提高辨识精度需要多次测量,此方法比较适用于基座不固定的小型磁悬浮转子系统.文献[12]提出了一种基于在线动平衡的磁力参数辨识方法,需要使用动平衡仪等专用设备对转子进行精确的动平衡,然后通过多次加重测试,计算磁力模型参数,过程较为复杂.
本文提出了一种基于不平衡响应的磁力参数辨识方法,利用转子的质量不平衡作为激励,通过对转子分别实施零位移控制和零电流控制,由系统自带的电流传感器和位移传感器检测同频电流响应和同频位移响应,根据在不同转速下测得的数据,解算磁力模型参数.
1 系统介绍以二自由度主动、三自由度被动的主被动磁悬浮转子系统为研究对象,进行磁轴承磁力模型参数辨识.图 1为主被动悬浮转子结构示意图.图中:H为磁轴承定子几何中心.被动磁轴承由定子永磁环和转子永磁环组成,实现轴向平动和径向扭转3个自由度的无源稳定悬浮;主动磁轴承为永磁偏置混合磁轴承,实现径向平动2个自由度的有源稳定悬浮.假设转子为非理想转子,仅存在静不平衡,进行径向平动自由度磁力参数的辨识.
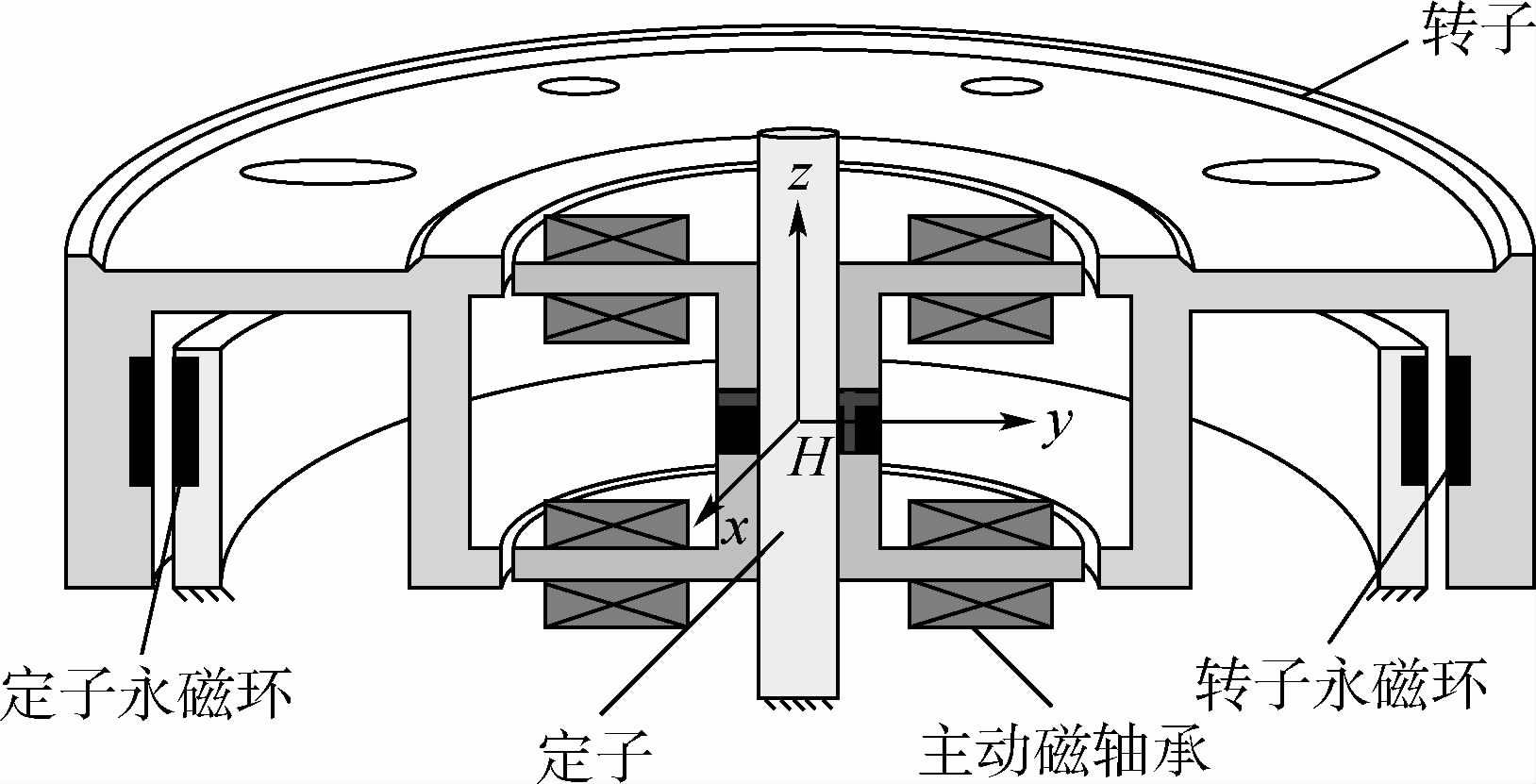 |
| 图 1 磁悬浮转子结构示意图Fig. 1 Framework diagram of magnetic bearing and rotor system |
| 图选项 |
永磁偏置混合磁轴承的磁力模型[3]为

式中:famb为主动磁轴承电磁力;Km为常系数;i0为等效偏置电流;i为磁轴承控制电流;x0为单边气隙长度;xd为转子偏移.在平衡位置(i=0、xd=0)附近对式(1)线性化得
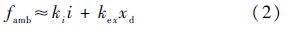
式中:ki为电流刚度;kex为主动磁轴承位移刚度.
被动磁轴承的径向力分量可以表示为[13]

式中:kp为被动磁轴承径向力位移刚度.结合式(2)和式(3),可得磁轴承对转子总的控制力为

式中:kx=kex+kp,为位移刚度.
设磁轴承转子几何中心为O,转子质心为C.在径向平面内建立以H为原点的固定坐标系Hxy和以O为原点的随动坐标系Oξη,如图 2所示.设在坐标系Hxy中,O的坐标为(xg,yg),C的坐标为(xc,yc),OC的距离为e,OC与Oξ的夹角为θ,转子角速度为Ω,逆时针为正,时间变量为t.
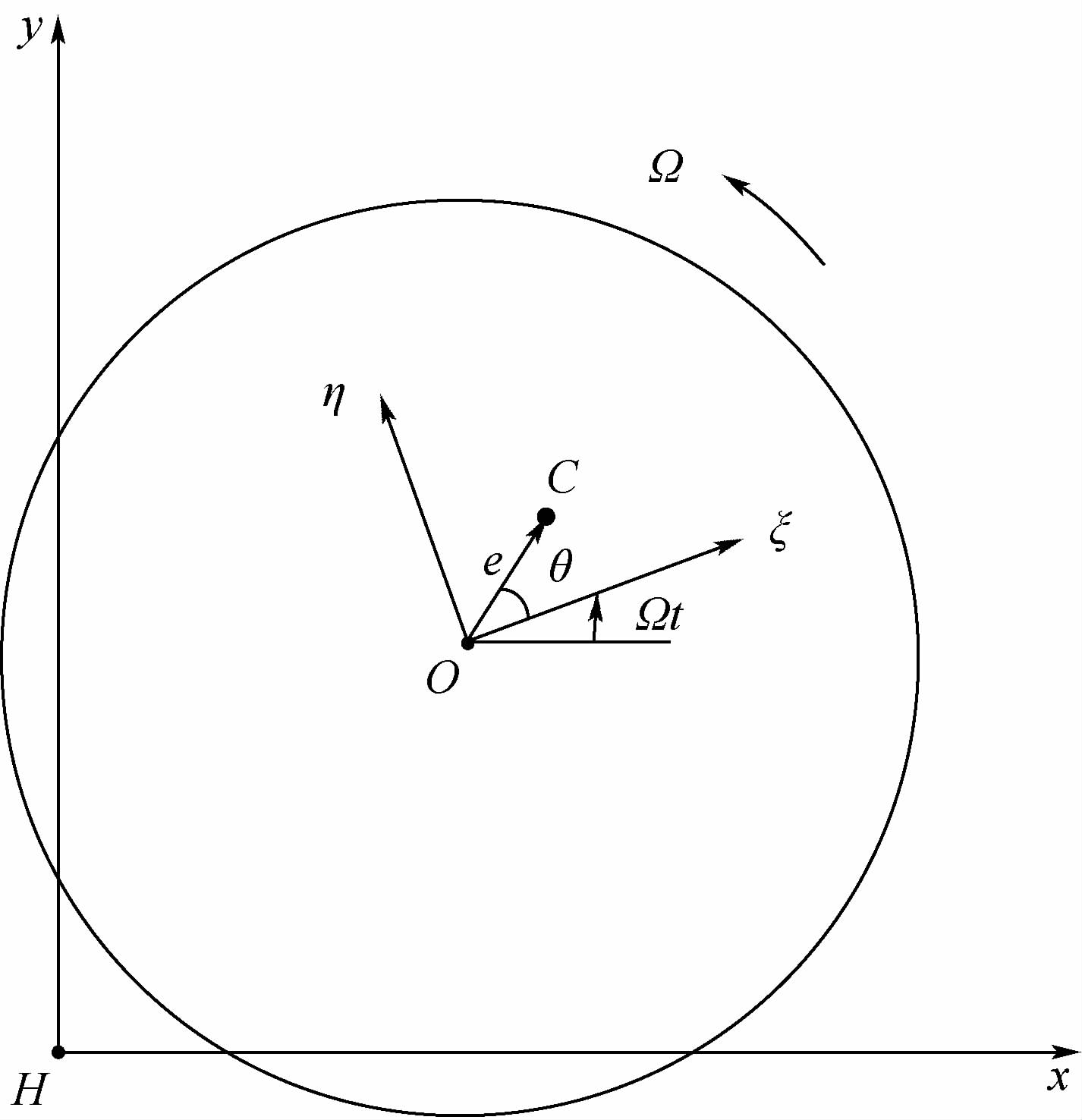 |
| 图 2 系统坐标系定义Fig. 2 System coordinate definition |
| 图选项 |
质心C与转子几何中心O的关系为
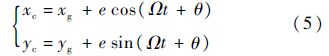
设x方向总的磁力为fxmb,y方向总的磁力为fymb,由牛顿第二定律得

式中:m为转子质量.将式(5)代入式(6),并结合磁力公式(4)可得
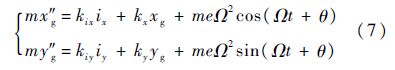
式中:kix和kiy分别为x方向和y方向的电流刚度;ix和iy分别为x方向和y方向的控制电流;kx和ky分别为x方向和y方向的位移刚度.
对转子实施转子几何中心的零位移控制,即xg=0、yg=0,由式(7)得
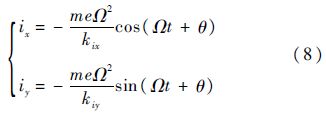
由式(8)可知,此时磁轴承控制电流为同频交流量.对转子实施磁轴承控制电流的零电流控制,即ix=0、iy=0,由式(7)得
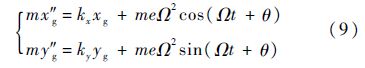
对式(9)求解可得

由式(10)可知,此时转子几何中心位移为同频交流量.对式(8)和式(10)只取幅值,可得
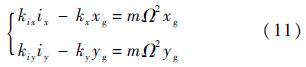
式中:ix、iy、xg及yg仅表示交流量幅值的大小.
在转速为Ω1和Ω2时分别进行零位移控制和零电流控制,测得x和y方向的同频电流和同频位移幅值分别为i1x、i1y、i2x、i2y和x1、y1、x2、y2,则由式(11)可得
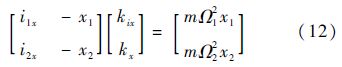
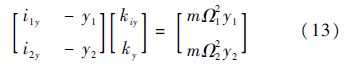
如果式(12)和式(13)等号左边的系数矩阵满秩,则由式(12)和式(13)即可解算磁力模型的电流刚度和位移刚度.以式(12)为例,对系数矩阵的元素求比,得
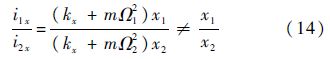
由式(14)可知,系数矩阵可逆,式(12)和式(13)有解.
2 控制器设计根据第1节的分析,基于不平衡响应的磁轴承磁力参数辨识需要对转子实施零位移控制和零电流控制.将转子的质量不平衡作用力视为对系统的同频扰动力,克服周期干扰的控制器类型有很多,如基于内模原理的重复控制器[14]、自适应控制器[15]和最常见的同频陷波器[16, 17]等.由于精确的磁力模型参数未知,只能基于理论设计值进行控制器的设计.为此采用通用陷波器方法[18],在系统原有稳定控制器前串联零位移控制器和零电流控制器,实现零位移控制和零电流控制,并通过设置T矩阵,保证闭环系统的稳定性.
以X通道为例,介绍控制器的设计.图 3为磁轴承闭环控制系统框图.图中:s为拉氏变换的复变量;Gc(s)为稳定控制器;Gw(s)为功放环节;P(s)为控制对象;ks为位移传感器放大倍数;N(s)为基于通用陷波器原理设计的零位移控制器和零电流控制器.具体通用陷波器设计框图如图 4所示.图中:Nf(s)为选频器;ε为陷波参数.
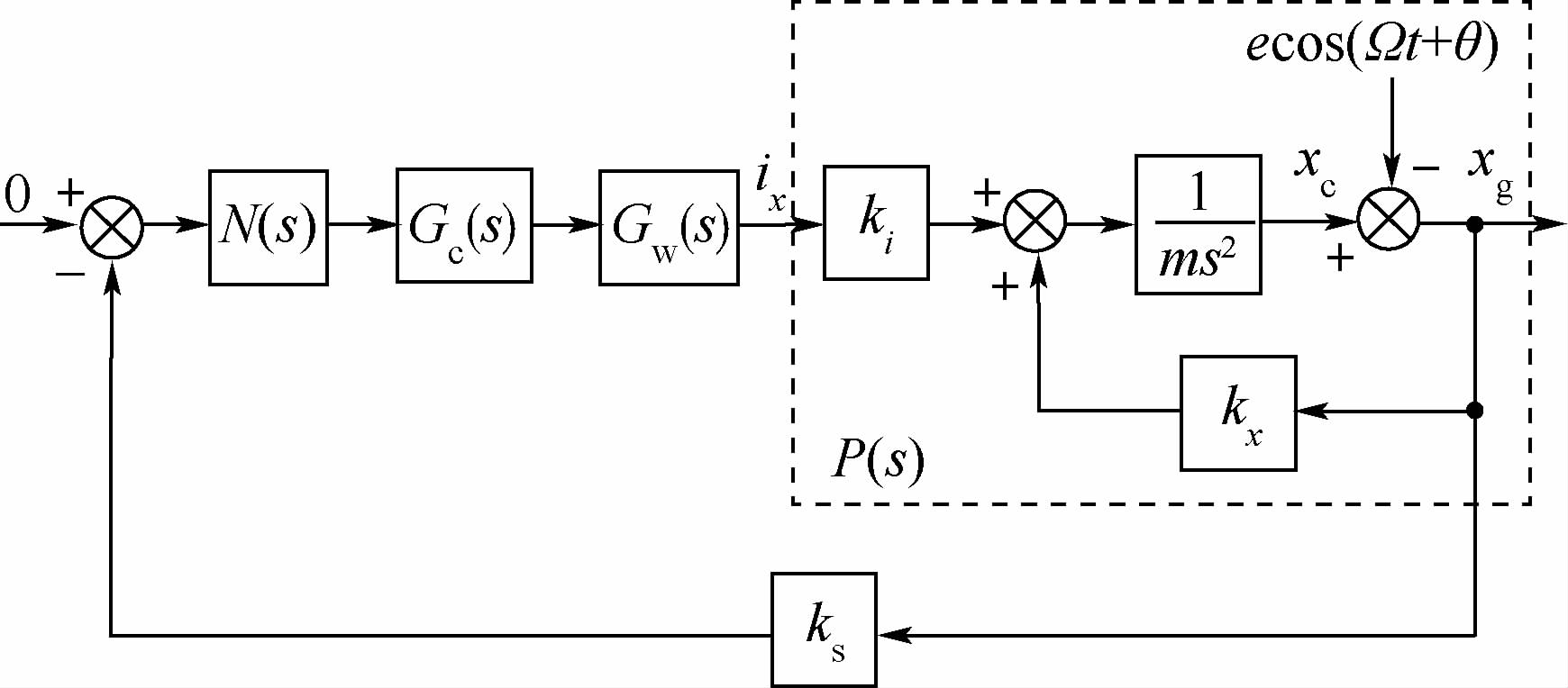 |
| 图 3 闭环控制系统框图Fig. 3 Block diagram of close-loop control system |
| 图选项 |
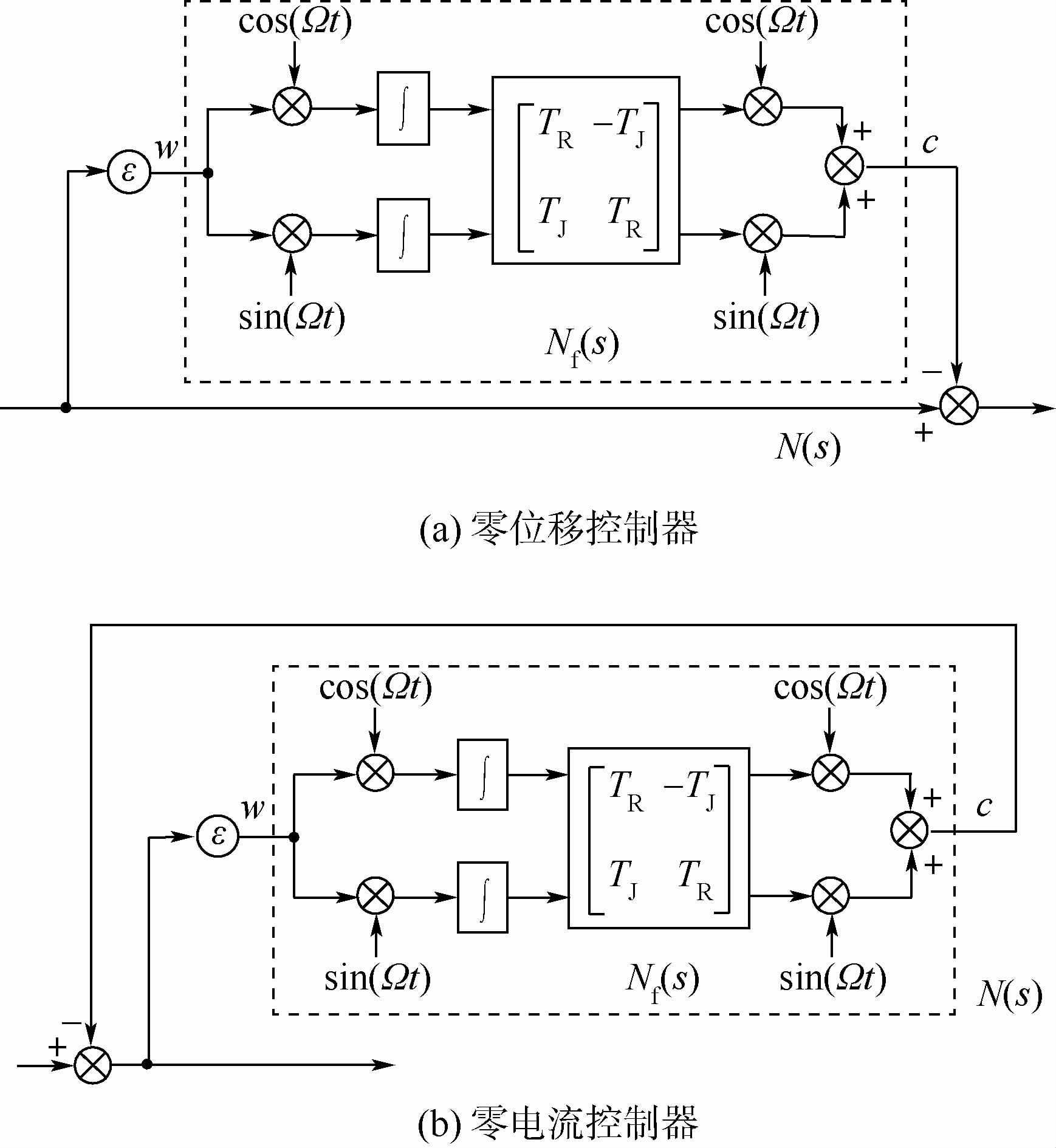 |
| 图 4 通用陷波器设计框图Fig. 4 Block diagram of generalized notch filter design |
| 图选项 |
Nf(s)和ε按照图 4所示的拓扑结构连接,分别实现零位移控制和零电流控制.令w(t)表示选频器的输入,c(t)表示选频器的输出,则选频器Nf(s)的时域表达式为
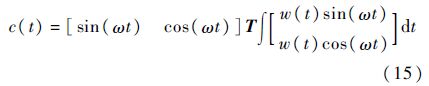
式中:T为由实系数元素TR和TJ组成的矩阵,具体形式为
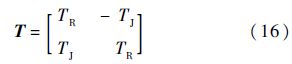
由式(15)可知,c(t)和w(t)满足微分方程:
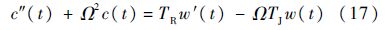
对式(17)取拉氏变换,则Nf(s)的传递函数为
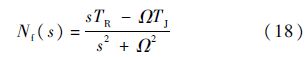
对于图 4(a)所示的零位移控制器,其传递函数N(s)为
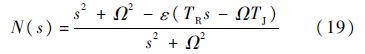
当ε≠0时,令s=jω,可得N(s)的幅频特性为

式中:Δω为N(s)的带宽,其大小由陷波参数ε决定.N(s)在转速同频点提供一个无穷大的增益,此时如果闭环系统渐进稳定,则N(s)输入信号中的同频量将趋于零,即实现了零位移控制.
对于图 4(b)所示的零电流控制器,其N(s)的传递函数为

当ε≠0时,令s=jω,可得N(s)的幅频特性为

由式(22)可知,只要闭环系统渐进稳定,N(s)的输出信号中不再含有与转速同频的成分,消除了Gc(s)和Gw(s)输入信号中的同频量,也就消除了同频电流响应,即实现了零电流控制.
3 闭环系统稳定性分析为保证闭环系统的稳定性,需要对T矩阵进行设计.借鉴文献[18]的设计方法将控制系统框图转换为图 5的形式.图中:S(s)为从选频器Nf(s)的输出到陷波参数ε的输入之间的传递函数,形式与系统灵敏度函数相似.因为稳定控制器Gc(s)保证未采用陷波器的原控制系统是稳定的,所以S(s)所有极点都具有负实部.
 |
| 图 5 闭环灵敏度函数与选频器闭环Fig. 5 Close loop of sensitivity function and filter |
| 图选项 |
结合式(18),图 5所示的系统闭环特征方程为
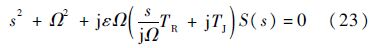
当ε=0时,有s=±jΩ.定义复变量T=TR+jTJ,对式(23)在ε=0、s=jΩ处求偏导得
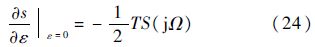
由于系统根轨迹关于ε是连续的,只要
 <0,则存在ε>0使系统特征根都有负实部.取T=S-1(jΩ),实部虚部分别对应TR和TJ,即得到T矩阵.
<0,则存在ε>0使系统特征根都有负实部.取T=S-1(jΩ),实部虚部分别对应TR和TJ,即得到T矩阵.4 实验验证利用北京航空航天大学研制的主被动双框架变速控制力矩陀螺进行实验验证,实验系统如图 6所示.磁轴承控制系统硬件采用DSP(Digital Signal Processor)+FPGA(Field Programmable Gate Array)的方案实现,其中DSP用于实现控制算法,FPGA用于完成时序与逻辑控制,系统控制周期为150 μs,功放采用PWM(Pulse-Width Modulation)调制,调制电源电压为28 V,载波频率为20 kHz.利用示波器读取同频电流和同频位移,采用Agilent DSO5014A数字示波器,带宽100 MHz,采样率达2 GSa/s.实验系统设计参数如表 1所示.
 |
| 图 6 磁悬浮控制力矩陀螺实验系统Fig. 6 Experiment system of magnetically suspended control moment gyro |
| 图选项 |
表 1 实验系统设计参数Table 1 Design parameters of experiment system
| 参数 | 数值 |
| m/kg | 2.146 |
| ks/(V·m-1) | 6 666.7 |
| ki/(N·A-1) | 167 |
| kx/(N·m-1) | 9.75×105 |
表选项
稳定控制器Gc(s)为工程常用的带不完全微分的PID(Proportion Integration Differentiation)控制器,经过现场调试使系统可以稳定悬浮,调试后的控制器参数为:比例系数Kp=6,积分系数Ki=18,微分系数Kd=0.006 4,微分时间常数Kf=0.000 28.功放环节Gw(s)近似为一阶低通环节,时间常数τ=5.4×10-5,放大系数Kv=0.272.
转子的质量不平衡,在高速下离心力效应比较显著,但是由于本实验系统采用主被动磁轴承支承形式,高速下被动自由度的波动及电机的磁偏拉力影响传感器的检测精度.为降低实验转速,在转子外缘增加2 g的静不平衡质量,分别在2 000 r/min和3 000 r/min下进行实验.实验波形如图 7所示.图中:ix和iy分别为x和y方向的磁轴承线圈电流.
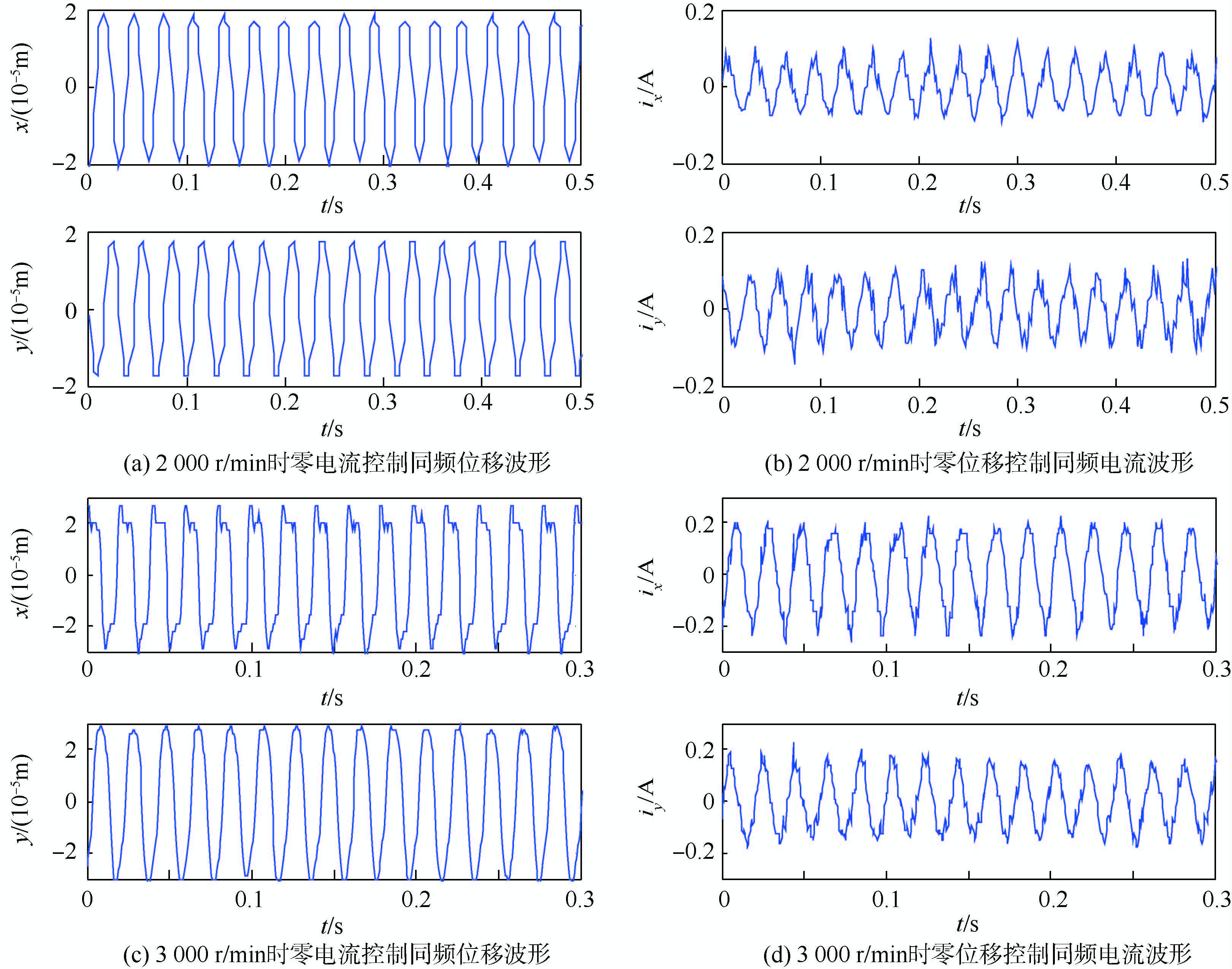 |
| 图 7 2 000 r/min和3 000 r/min时零电流控制和零位移实验控制波形Fig. 7 Experiment oscillograms of null-current control and null-displacement control at 2 000 r/min and 3 000 r/min respectively |
| 图选项 |
由图 7可知,x方向和y方向的实验结果基本一致.由于直接采样获得的数据存在高频噪声污染,用MATLAB程序对采样数据进行滤波处理后,提取基频信号.2 000 r/min时同频位移幅值约为19 μm,同频电流幅值约为0.13 A;3 000 r/min时同频位移幅值约为31 μm,同频电流幅值约为0.22 A.解算得出磁轴承电流刚度为179.6 N/A,位移刚度为1.13×106 N/m.电流刚度实验值与设计值的偏差率为7%,位移刚度实验值与设计值的偏差率为15.9%.位移刚度偏差较大与被动磁轴承的位移刚度非线性有关,转子偏离平衡位置处被动磁轴承的位移刚度大于平衡位置处的位移刚度,而零电流控制时转子几何中心偏离平衡位置.因此,实验辨识的是偏离平衡位置处的综合位移刚度,辨识值比理论设计值大.
实验中零电流控制和零位移控制的控制精度及采样数据的噪声水平是影响辨识精度的重要因素.本文通过降低实验转速,减弱了被动自由度及电机磁偏拉力等外部干扰作用;通过对采样数据进行离线数据处理,去除了测量噪声,进一步提高了辨识的准确度.
5 结 论1) 基于转子不平衡响应的磁轴承磁力参数辨识方法仅需要磁轴承控制系统自带的位移传感器和电流传感器,不需要安装测力计等外部仪器设备,方法简单易行,适用范围广.
2) 利用转子的不平衡质量作为激励,不需要反复试重,一次启车即可完成,效率高,经济性好.
参考文献
| [1] | 刘强, 房建成. 磁悬浮飞轮用可重复抱式锁紧装置[J].光学精密工程, 2012, 20(8): 1802-1810. Liu Q, Fang J C.Repeated clamping locking device for magnetic bearing flywheel[J].Optics Precision Engineering, 2012, 20(8): 1802-1810(in Chinese). |
| Cited By in Cnki (12) | |
| [2] | Zheng S Q, Han B C.Investigations of an integrated angular velocity measurement and attitude control system for spacecraft using magnetically suspended double-gimbal CMGs[J].Advances in Space Research, 2013, 51(12): 2216-2228. |
| Click to display the text | |
| [3] | 王英广, 房建成, 郑世强, 等.磁悬浮电机的高效高精度在线动平衡[J].光学精密工程, 2013, 21(11): 2884-2892. Wang Y G, Fang J C, Zheng S Q, et al.Field balancing of magnetically levitated motor in high-efficiency and high-accuracy[J].Optics and Precision Engineering, 2013, 21(11): 2884-2892(in Chinese). |
| Cited By in Cnki (2) | |
| [4] | 魏彤, 向岷.磁悬浮高速转子基于位移刚度力超前前馈补偿的高精度自动平衡方法[J].机械工程学报, 2012, 48(16): 184-191. Wei T, Xiang M.Autobalancing for magnetically suspended high-speed rotors based on lead feedforward compensation for displacement stiffness force[J].Journal of Mechanical Engineering, 2012, 48(16): 184-191(in Chinese). |
| Cited By in Cnki (3) | |
| [5] | Fang J C, Wang C E, Wen T.Design and optimization of a radial hybrid magnetic bearing with separate poles for magnetically suspended inertially stabilized platform.[J].IEEE Transactions on Magnetics, 2014, 50(5): 1-11. |
| Click to display the text | |
| [6] | Han B C, Zheng S Q, Le Y, et al.Modeling and analysis of coupling performance between passive magnetic bearing and hybrid magnetic radial bearing for magnetically suspended flywheel[J].IEEE Transactions on Magnetics, 2013, 49(10): 5356-5370. |
| Click to display the text | |
| [7] | Han B C. Modeling and analysis of novel integrated radial hybrid magnetic bearing for magnetic bearing reaction wheel[J].Chinese Journal of Mechanical Engineering, 2010, 23(5): 655-662. |
| Click to display the text | |
| [8] | Kim S J, Lee C W.On-line identification of current and positon stiffnesses by LMS algorithm in active magnetic bearing system equipped with force transducers[J].Mechanical Systems and Signal Processing, 1999, 13(5): 681-690. |
| Click to display the text | |
| [9] | 白金刚, 张小章, 张剀, 等.磁悬浮储能飞轮系统中的磁轴承参数辨识[J].清华大学学报: 自然科学版, 2008, 48(3): 382-385. Bai J G, Zhang X Z, Zhang K, et al.Parameter identification for active magnetic bearings in energy storage flywheel[J].Journal of Tsinghua University: Science and Technology, 2008, 48(3): 382-385(in Chinese). |
| Cited By in Cnki (17) | |
| [10] | 郑世强.双框架磁悬浮控制力矩陀螺磁轴承控制及应用研究[D].北京: 北京航空航天大学, 2011. Zheng S Q.Magnetic bearing control and application research of double gimbal magnetically suspended control moment gyro[D].Beijing: Beijing University of Aeronautics and Astronautics, 2011(in Chinese). |
| Click to display the text | |
| [11] | 房建成, 王鹏.控制力矩陀螺用磁轴承磁力参数的辨识[J].中国惯性技术学报, 2007, 15(2): 221-224. Fang J C, Wang P.Identification of magnetic parameters for magnetic bearings in control moment gyroscope(CMG)[J].Journal of Chinese Inertial Technology, 2007, 15(2): 221-224(in Chinese). |
| Cited By in Cnki (2) | |
| [12] | 侯二永, 刘昆. 基于在线动平衡的磁轴承参数辨识[J].国防科技大学学报, 2013, 35(6): 65-70. Hou E Y, Liu K.Parameter identification for magnetic bearing based on online dynamic balancing[J].Journal of National University of Defense Technology, 2013, 35(6): 65-70(in Chinese). |
| Cited By in Cnki | |
| [13] | 文通.主被动磁悬浮反作用飞轮永磁偏置混合磁轴承控制方法研究[D].北京: 北京航空航天大学, 2012. Wen T.Study on control of the permanent magnet biased magnetic bearing used in the active-passive hybrid magnetic suspended reaction flywheel[D].Beijing: Beijing University of Aeronautics and Astronautics, 2012(in Chinese). |
| Click to display the text | |
| [14] | 陈振, 刘向东, 戴亚平, 等.一种改进的重复控制器在高频角振动转台中的应用[J].电工技术学报, 2008, 23(11): 178-182. Chen Z, Liu X D, Dai Y P, et al.A modified repetitive controller and its application to high-frequency angular-vibration table[J].Transactions of China Electrotechnical Society, 2008, 23(11): 178-182(in Chinese). |
| Cited By in Cnki (4) | |
| [15] | Shi J, Zmood R, Qin L.Synchronous disturbance attenuation in magnetic bearing systems using adaptive compensating signals[J].Control Engineering Practice, 2004, 12(3): 283-290. |
| Click to display the text | |
| [16] | 彭晓军, 高钟毓, 王永樑.磁电轴承中抑制不平衡振动的陷波器设计方法[J].机械工程学报, 2006, 42(6): 120-123. Peng X J, Gao Z Y, Wang Y L.Design of notch filter to eliminate unbalance vibration in magnetic and electrostatic bearing[J].Journal of Mechanical Engineering, 2006, 42(6): 120-123(in Chinese). |
| Cited By in Cnki (8) | |
| [17] | 冯锐, 郑世强, 房建成.高速磁悬浮电动机对拖试验中转子不平衡量在线辨识与振动控制[J].机械工程学报, 2014, 50(3): 71-77. Feng R, Zheng S Q, Fang J C.Online identification and unbalanced vibration control of high-speed magnetically levitated motor for drag test[J].Journal of Mechanical Engineering, 2014, 50(3): 71-77(in Chinese). |
| Cited By in Cnki (1) | |
| [18] | Herzog R, Buhler P, Gahler C, et al.Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings[J].IEEE Transactions on Control Systems Technology, 1996, 4(5): 580-586. |
| Click to display the text |
