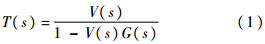
K-π散射中相应的V(s)参考了文献[10, 12]的结果:
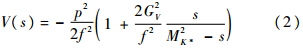
式中:MK*为K*的裸质量;f为π(K)介子的衰变常数;GV为一个标量介子耦合到两个赝标介子的耦合常数.可以看到式(2)中的势能V(s)的表达式与文献[11]中稍有不同,这是因为在文献[11]中p2因子被G(s)函数吸收,所以V(s)不依赖于动量.对质量分别为mπ和mK的两个介子,即K-π传播子的G(s)函数定义为
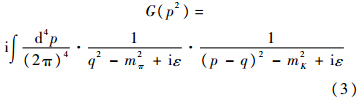
式中:p为外部的介子-介子系统的四动量;π为圆周率;i为虚数.对于圈积分的正规化有多种方法.在文献[11]中,作者采用了动量截断的方法,但是在本文中,本文用到的是维数正规化的方法,这种方法用来研究有限体积内的K-π相互作用更加方便.通过使用场论中维数正规化的方法,可以得到G(s)函数的表达式:
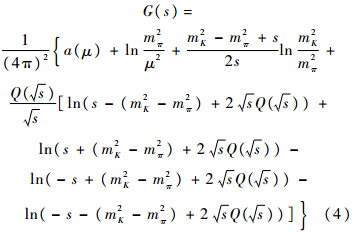
式中:s=p2;Q(s)为粒子的在壳动量;μ为正规化能模;a(μ)为重整化减除常数.本文是在质心系框架中进行的,系统能量为E=
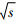.在式(4)中,还有两个正规化参数： 
f和GV这两个参数采用文献[11]中的结果:
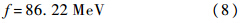
但是MK*的值与文献[11]中不同,这是因为在本文中采用的是维数正规化方法,而不是动量截断的正规化方法.本文中,与P波中K-π散射的相移的实验数据进行拟合,从而得到
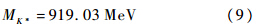
上述公式均是在连续空间情况下的表达式.在本文中,如果研究有限体积下的K*介子,那么只需要通过有限盒子的大小L来转化式(4)中的G(s)函数,即在满足周期性边界条件的情况下,把积分形式转化为对离散动量求和的形式.将离散动量求和得到的G(s)函数重新定义为Gf(s,L),可得
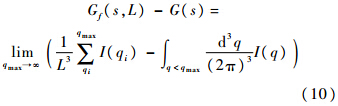
式中:求和过程中的分立动量由式(11)给出；而I(qi)函数由式(12)给出:
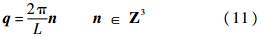
图 1为Gf(s,L)－G(s)的实部随qmax变化的曲线,本文L=2.5 mπ－1,E=800 MeV.从图中可以看到，当qmax超过3 000 MeV时,曲线的收敛效果很好.然而,在计算中为了节省计算时间,仍然对较小的qmax的值取平均值来获得最后的结果.
 |
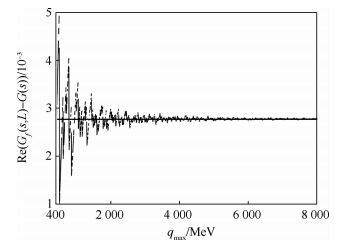| 图 1 Gf(s,L)－G(s)的实部随qmax的变化Fig. 1 Real part of Gf(s,L)－G(s) changing with qmax |
| 图选项 |
2 利用手征幺正方法计算能级为了计算P波的K-π散射振幅的能级,可以通过求式(13)的解寻找T(s)矩阵的极点:
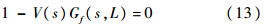
本文的Gf(s,L)是定义在有限体积条件下的,可以通过式(10)得到.从式(10)可以很清楚地看到K-π散射的能级是立方体盒子的大小L和π介子质量mπ的函数.本文的研究方法与文献[2, 3, 4, 5, 6, 7, 15]类似.首先讨论能级对于盒子大小L的依赖性.图 2中是能级随L变化的曲线,其中能级是通过对1 200～2 000 MeV范围内的不同qmax时的能级求取平均值得到.
 |
| 图 2 能级与立方体盒子的大小L的函数关系Fig. 2 Energy levels as a function of cubic box size L |
| 图选项 |
为了和格点的结果进行比较,需要改变π介子质量并重新进行计算.假定mπ0是π介子的物理质量,而mπ成为一个自由参数.其他的参数则会随着mπ的变化而变化.将参数f定义为关于mπ的函数,其关系为[16, 17, 18]
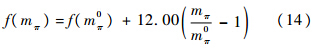
式中：f(mπ0)=86.22 MeV是在拟合K*介子数据时用到的数值.耦合常数GV与f的变化相关,假设其与f成正比,因此有GV=
.另外,假设式(2)中的K*介子的裸质量MK*与mπ是不相关的.使用上述结果就可以计算mπ取非物理值时的结果并与格点的结果比较.在文献[10]中,格点组用mπ=266 MeV进行计算得到了能级E1=(915.6±3.0)MeV和E2=(1 522.3±7.0)MeV.本文也选取mπ=266 MeV进行了有限体积的计算，得到的结果为E1=(924.0±8.9)MeV和E2=(1 483.0－2.3+2.4)MeV.和格点组得到的结果进行对照可以发现,两者差别不大.3 利用能级计算相移相移可以从上面计算的能级获得.遵循文献[3]中使用的方法,利用式(15)来计算K-π散射在P波中的相移: 
式中:散射振幅不仅是能量E的函数,也是盒子尺寸L的函数,因此,T(E,L)由式(16)给出:
利用式(13)将V(E)换成
(E,L)－1,能量值使用图 2所示的最低能级.这些过程中可以使用所有能级,但因为所使用的手征幺正方法是一个对低能适用得更好的有效理论,所以采用最低能级来计算相移.计算结果如图 3所示. |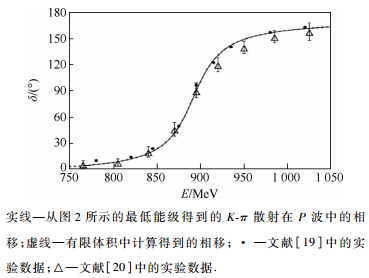
| 图 3 K-π散射在P波中的相移Fig. 3 K-π scattering in P-wave phase shifts |
| 图选项 |
通过上述得到的相移δ(E)可以拟合出K*介子的物理性质,计算mK*、gK*πK和ΓK*.需要注意的是mK*是本文计算得出的K*介子的质量,是本文的输出量之一;而MK*是K*介子的裸质量,是本文的输入量之一.使用文献[7, 21]中用到的两个公式来计算K*介子的性质:
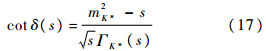
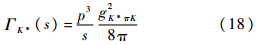
式(18)中的因子8π是本文归一化因子,在文献[22]中使用的是6π.本文使用K-π散射的最低能级,通过拟合相移数据得到的结果为
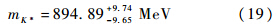
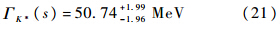
在上述计算结果中,理论上的不确定度是根据文献[7]中的方法进行计算的,本文假定式(2)中的3个参数GV、MK*和f的不确定度为1%.这样,能级和相移的不确定度不大,如图 4和图 5所示.特别地,如果固定L=2.0 mπ－1,则能级的不确定度小于1%,那么,相移在能量为E=900 MeV附近的关联不确定度约为5%.这些结果与文献[23]的实验结果相比符合得很好.
 |
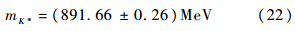
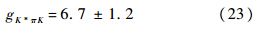
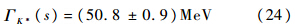
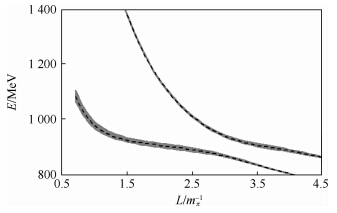| 图 4 能级的不确定度Fig. 4 Uncertainty of energy levels |
| 图选项 |
 |
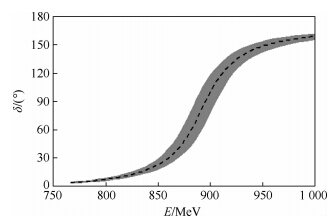| 图 5 相移的不确定度Fig. 5 Uncertainty of phase shifts |
| 图选项 |
4 结 论1) 手征幺正方法已经被成功地应用于无限空间中K-π相移的计算,在这基础上,本文研究了有限体积中的P波K-π相互作用,通过计算得到了作为立方体盒子尺寸L和π介子质量函数的P波K-π散射振幅的能级.2)在mπ取非物理值时,通过计算得到了P波K-π散射振幅的能级,得到的结果与相应的格点QCD计算得到的结果基本一致.3)采用结论2)中计算得到的最低能级,计算了K-π散射的相移,与实验结果符合得也比较好.4)通过计算得到的相移结果,拟合得到了作为输出结果的K*介子的物理性质,与实验结果符合得很好.致谢 感谢Oset E教授对该问题的建议和无私的帮助,同样感谢孙宝玺博士、肖楮文博士和任修磊博士有益的讨论.
参考文献
| [1] | Lüscher M.Volume dependence of the energy spectrum in massive quantum field theories II:Scattering states[J].Communication in Mathematical Physics, 1986, 105(2):153-188. |
| Click to display the text | |
| [2] | Döring M, Meiβner U G, Oset E, et al.Unitarized chiral perturbation theory in a finite volume:Scalar meson sector[J].European Physical Journal A, 2011, 47(11):139-1-139-15. |
| Click to display the text | |
| [3] | Döring M, Haidenbauer J, Meiβner U G, et al.Dynamical coupled-channel approaches on a momentum lattice[J].European Physical Journal A, 2011, 47(12):163-1-163-7. |
| Click to display the text | |
| [4] | Torres A M, Dai L R, Koren C, et al.The KD, ηDs interaction in finite volume and the Ds*0 (2317) resonance[J].Physical Review D, 2012, 85(1):014027. |
| Click to display the text | |
| [5] | Döring D, Meiβner U G.Finite volume effects in pion-kaon scattering and reconstruction of the κ (800)resonance[J].Journal of High Energy Physics, 2012, 1201:009. |
| Click to display the text | |
| [6] | Roca L, Oset E.Scattering of unstable particles in a finite volume:The case of πρ scattering and the a1(1260) resonance[J].Physical Review D, 2012, 85(5):054507. |
| Click to display the text | |
| [7] | Chen H X, Oset E.ππ interaction in the ρ channel in finite volume[J].Physical Review D, 2013, 87(1):016014. |
| Click to display the text | |
| [8] | Lang C B, Luka L, Daniel M, et al.Kπ scattering for isospin 1/2 and 3/2 in lattice QCD[J].Physical Review D, 2012, 86(5):054508. |
| Click to display the text | |
| [9] | Fu Z, Fu K.Lattice QCD study on K* (892)meson decay width[J].Physical Review D, 2012, 86(9):094057. |
| Click to display the text | |
| [10] | Oller J A, Oset E.N/D description of two meson amplitudes and chiral symmetry[J].Physical Review D, 1999, 60(7):074023. |
| Click to display the text | |
| [11] | Xiao C W, Aceti F, Bayar M.The small K-π component in the K* wave functions[J].European Physical Journal A, 2013, 49(2):22. |
| Click to display the text | |
| [12] | Oller J A, Oset E.Chiral symmetry amplitudes in the S wave isoscalar and isovector channels and the σ, f0 (980), a0 (980)scalar mesons[J].Nuclear Physics A, 1997, 620(4):438-456. |
| Click to display the text | |
| [13] | Oller J A, Meissner U G.Chiral dynamics in the presence of bound states:Kaon nucleon interactions revisited[J].Physics Letters B, 2001, 500(3-4):263-272. |
| Click to display the text | |
| [14] | Oller J A, Oset E, Palomar J E.Pion and kaon vector form-factors[J].Physical Review D, 2001, 63(11):114009. |
| Click to display the text | |
| [15] | Xie J J, Oset E.The DN, πΣc interaction in finite volume and the Λc(2595) resonance[J].European Physical Journal A, 2012, 48(10):146. |
| Click to display the text | |
| [16] | Boucaud P, Dimopoulos P, Farchioni F, et al.Dynamical twisted mass fermions with light quarks[J].Physics Letters B, 2007, 650:304-311. |
| Click to display the text | |
| [17] | Beane S R, Luu T C, Orginos K, et al.Precise determination of the I=2 ππ scattering length from mixed-action lattice QCD[J].Physical Review D, 2008, 77(1):014505. |
| Click to display the text | |
| [18] | Noaki J, Aoki S, Chiu T W, et al.Light meson spectrum with Nf=2+1 dynamical overlap fermions[C]//Proceddings, 26th International Symposium on Lattice Field Teory (Lattice 2008).Italy:PoS Lattice, 2008:107. |
| [19] | Estabrooks P, Carnegie R K, Martin A D, et al.Study of K-π scattering using the reactions K±p→K±π+n and K±p→K±π-Δ++ at 13-GeV/c[J].Nuclear Physics B, 1978, 133(3):490-524. |
| Click to display the text | |
| [20] | Mercer R, Antich P, Callahan A, et al.K-π scattering phase shifts determined from the reactions K+p→K+π-Δ++ and K+p→K0π0Δ++[J].Nuclear Physics B, 1971, 32(2):381-414. |
| Click to display the text | |
| [21] | Lang C B, Mohler D, Prelovsek S, et al.Coupled channel analysis of the ρ meson decay in lattice QCD[J].Physical Review D, 2011, 84(5):054503. |
| Click to display the text | |
| [22] | Prelovsek S, Leskovec L, Lang C B, et al.Kπ scattering and the K* decay width from lattice QCD[J].Physical Review D, 2013, 88(5):054508. |
| Click to display the text | |
| [23] | Beringer J, Arguin J F, Barnett R M, et al.Review of Particle Physics[J].Physical Review D, 2012, 86(1):010001. |
| Click to display the text |
