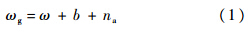
式中:ωg为陀螺测量值;ω为角速率真值;b为陀螺仪的常值漂移;na为量测噪声.对于量测噪声na,其误差特性比较复杂,其误差中也可能包含一定的规律性,可以针对陀螺仪模型中的量测噪声na项,深入分析其特性,寻找测量噪声部分的规律性,对其进行误差建模.利用GP+GA算法对量测噪声部分进行建模,利用遗传规划建立量测噪声的模型结构,然后利用遗传算法对建立的模型结构进行参数优化.使最后的模型结构为
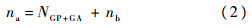
式中：NGP+GA为由GP+GA建模方法得到的原子自旋陀螺仪随机漂移误差中非线性部分的模型；nb为量测噪声剩余部分.通过对量测噪声的进一步建模,使陀螺的性能得到提升.2 GP+GA随机误差建模过程分析2.1 数据的采集和预处理陀螺噪声信号是连续信号,建模过程中需要对连续信号进行采样.以z轴的激光陀螺为例,z轴陀螺的标称角速度为10(°)/h,陀螺仪的脉冲当量为84.25,采样频率为100 Hz,即每10 ms采集一次陀螺输出的瞬时数据.预处理主要是对采样后的时序进行相应的处理,对于激光陀螺仪而言,就是根据脉冲当量和采样频率等参数得到离散的时间间隔为10 ms的陀螺仪输出角速度值.为了使建立的模型更加准确,对于数据波动较小的数据,需要对数据进行平移,即可以将数据同时减掉一常数项,以使其波动相对更加明显.本文中是将陀螺仪的输出转化的角速度数据进行零化处理,即将原序列去掉均值后得到新的序列.2.2 函数集和端点集的确定及初始代的生成在GP建模中函数集的选取至关重要.函数集中函数的多少和函数的类型决定了建立的模型复杂程度.函数过少会使建立的模型精度不高;函数过多会使搜索空间太大从而影响建模效果甚至得不到任何模型结果.本文陀螺漂移建模选择的函数集为
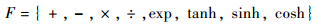
其中：{+,－,×,÷}为基本的算术运算函数集,基本的多项式函数和简单的非线性函数可以通过基本算术运算函数集的组合得到;{exp}为指数函数;{tanh,sinh,cosh}为基本的三角函数集.考虑到函数集的选择决定了模型的复杂性,所以本文的函数集设置为上述几种,这几种函数通过组合基本可以反映出模型的线性部分和非线性部分趋势,可以满足本文的建模需求.选取的端点集为:T={x1,x2,x3,x4,A},其中X={x1,x2,x3,x4}是所有自变量所组成的集合.其中x1=ω(t-1)是t-1时刻的角速度;x2=ω(t-2)是t-2时刻的角速度;x3=ω(t-3)是t-3时刻的角速度;x4=ω(t-4)是t-4时刻的角速度;A为常数集,是数学表达常系数.将由函数集F和端点集X出发生成的一系列随机二叉树作为初始群体,群体中的每一个成员都是随机产生的一棵有根结点且具有有序分支的二叉树.群体的规模是根据实际情况设置的一个重要参数.根节点必须是一个运算符,其值只能从函数集F中随机选择;叶子节点只能从终止集T中随机选择;其余的非叶子节点可以从集合F∪T随机选择.2.3 适应度函数的确定本文以方差最小为指导思想,利用最小二乘原理设计适应度函数.GP建模过程中采用的自适应评价函数为
式中:N为建模数据的总个数;Aansw[i]为陀螺仪第i个实际输出的数据;Yyavg为Aansw数组中N个实际输出数据的平均值,若实际输出数据一定,Yyavg为一定值;TtempGPAnswer[i]为GP建立模型中第i个对应的陀螺仪输出角速度值.由式(3)可知:当实际数据已知的情况下分母的大小已确定,即
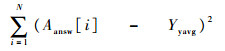是个常数;
是和每次建立的模型相关的部分,模型越接近真实输出,即模型越准确,那么其对应值越小.综上所述,FGP的值越大,说明建立的模型越准确.用上述适应度函数来表征建模的好坏是比较合理的.2.4 选择和复制根据适应度的大小选择根据陀螺输出数据建立的模型.在选择的过程中多个模型先被随机地选择,然后比较本组模型的适应值大小,最后选择最好的模型代替最差的模型.由于之前选择的最优模型会再次回到当前代中,所以适应值较高的模型被多次选择和复制.通过这种方式,适应值较优的模型比适应值较差的模型被复制的可能性较大,这正体现了“适者生存”的进化思想.2.5 交叉和变异之前被选择的模型个体被一些进化的操作来优化,并且被保留到下一代中.GP数据建模就是通过使用遗传操作来动态地改变模型结构,反复地将问题的函数集和端点集递归地组合,得到数据的模型结构,交叉和变异是其中最简单也是最有用的遗传操作.在交叉的过程中,在父代个体中独立地选取二叉树的某个节点为杂交点,交换父代个体中以杂交点为根节点的相应子树得到两个子代个体.变异过程中,在父代个体中随机选择某个节点为变异点,随机执行变异操作.2.6 GA优化参数在上述GP建模过程中,得到了模型的基本结构,但是此时模型的结构参数并不能保证最优,所以可以在已建立的模型结构的基础上用GA进一步对模型参数进行优化,GA优化参数时根据具体情况设置种群数量、迭代次数、交叉概率、变异概率等参数,算法采用二进制编码方式,对GP模型中的参数a、b、c进行编码优化.在优化过程中,为了节省优化的时间及减少优化陷入局部最优的问题,模型系数的优化范围应该合适:范围过大会导致模型优化时间太长,范围过小会导致寻找不到区间内的最值.本GA算法中以建模前后陀螺仪角速度方差的倒数作为自适应评价函数:
式中:N为输入的原始数据的总个数；y(i)为GP建立的最优模型里对应的陀螺输出数据；yGA(i)为GA建模优化之后得到的第i时刻模型的相应计算值；模型的结构系数为GA优化算法中的优化参数a、b、c.在结果中寻找适应度最大时对应的参数a、b、c的值就是本文寻找的最优参数值.3 实验及结果分析在以上理论基础上,采集激光陀螺的z轴输出数据并进行分析建模.采用的激光陀螺的脉冲当量为84.25,采样频率为100 Hz,激光陀螺仪z轴的理论角速度为10(°)/h.首先将陀螺输出的一系列脉冲个数转换为陀螺输出的角速度,转换方式为:陀螺角速度=脉冲个数×脉冲当量÷3 600.转化得到一系列角速度值,单位为(°)/h.图 1为将采集的陀螺漂移原始测量信号转换为角速度的输出数据.从数据分析可知,此时陀螺输出角速度的均值为9.995 1(°)/h.
 |
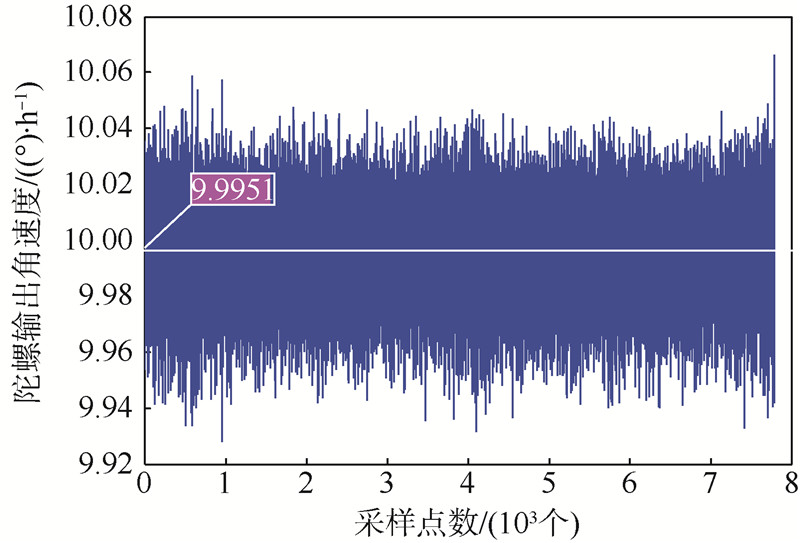| 图 1 陀螺漂移原始测量转换输出数据Fig. 1 Output data transformed from originally |
| 图选项 |
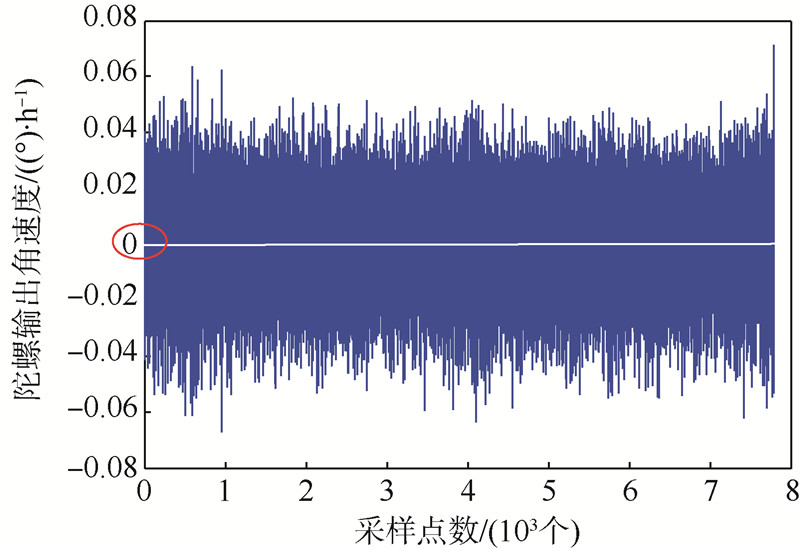
为了更加方便地建立陀螺的随机漂移误差模型,本实验中首先将转变之后的陀螺仪数据减掉数据的平均值,得到零均值的陀螺漂移数据.图 2为进行去均值后的陀螺仪数据.将处理后的零均值的陀螺仪角速度数据进行相关处理,得到当前t时刻和之前t－1~t－4时刻的对应数据,将其t－1~t－4时刻的对应数据分别作为GP的输入x(t－1)~x(t－4),当前时刻的数据作为陀螺仪的输出Y(t).GP算法中:种群数量为1 000,迭代的次数为200,采用7 793组对应数据对陀螺漂移误差建立模型,建模的结果为
 |
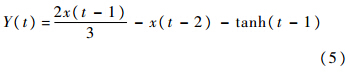
| 图 2 去均值后的陀螺漂移数据Fig. 2 Non-mean data of gyroscope’s drift |
| 图选项 |
在GP建模的基础上继续对模型中的参数进行优化.GA优化参数时设置参数如下:最大迭代次数为200次,种群数量为50次,交叉概率为0.6,变异概率为0.1,GA优化模型参数时以建模前后陀螺仪角速度方差的倒数作为自适应评价函数,见式(4).对上述GP算法建立的模型进行参数优化,其中a、b、c为模型中待优化的模型系数:
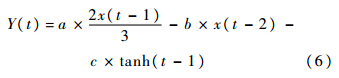
在优化过程中,为节省优化的时间及减少优化陷入局部最优的问题,系数a,b,c∈[－4.5,4.5].GA优化参数的方差优化曲线如图 3所示.
 |
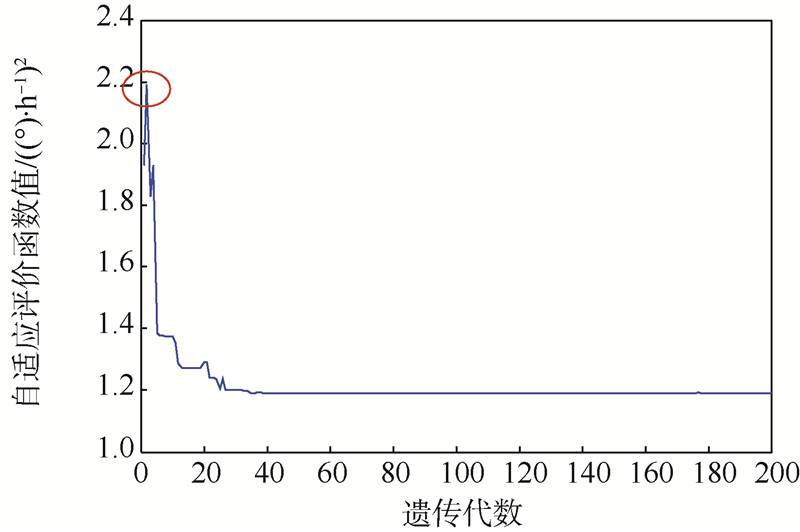| 图 3 GA优化参数的方差优化曲线Fig. 3 Squre curve of optimized parameter by GA |
| 图选项 |
从图 3可以看出，从0~200代之间GA的自适应评价函数值在第2代时取得最大值,此时自适应评价函数值为2.192.从式(4)可知:遗传算法优化方差大小和自适应评价函数值的大小成反比.所以自适应评价函数的最大值对应的即为优化方差的最小值.当方差取最小值时对应的陀螺随机误差模型优化系数为a=0.995 0,b=0.838 8,c=1.747 7,此时陀螺漂移方差最小约为1.1834.所以陀螺随机漂移最优模型表达式为
将本文提出的GP+GA建模方法和传统AR建模方法进行对比.在AR建模中,时间序列数据必须满足零均值的正态性和稳定性,所以需要对数据进行去均值化处理.本文中数据稳定性和正态性都满足要求.在预处理之后,时间序列数据能够满足AR建模方法的要求.在AR建模过程中首先需要确定模型的阶数和AR模型的相关系数.Alaike信息准则用来确定模型的阶数.最小均方差用来确定模型的最优系数.在本文中,结果显示AR(4)模型有最小的均值方差和最小的AIC(Akaike Information Criterion)值,所以本文中AR(4)被选为最优模型结构.将建模优化之前,AR建模方法和本文中的GP+GA建模方法得到的角速度方差进行综合对比,将方差对比结果列于表 1中.从表 1中可以看出:模型优化之前的方差约为4.503 5 ((°)/h)2;用传统的AR建模优化方法对陀螺随机误差建模分析之后方差为1.396 1 ((°)/h)2;用GP进行建模分析方差降为1.289 9 ((°)/h)2,进一步用GA对GP建立的模型进行参数优化,得到最终的方差为1.183 4 ((°)/h)2.可见,经过GP+GA对陀螺漂移误差建模优化之后,漂移的方差降低了73.72%,与经典的AR建模方法相比,陀螺仪优化方差减低了4.72%.由此可见:与经典的AR建模方法相比,GP+GA建模方法可以更有效补偿陀螺仪的随机漂移误差,进而提高陀螺仪的精度.优化前后陀螺漂移角速度对比如图 4所示.表 1 GP+GA优化前后陀螺随机漂移方差对比Table 1 Squre error contrast of gyroscope’s random drift before and after optimized by GP+GA
| 状态 | 方差/((°)·h-1)2 |
| 优化之前 | 4.5035 |
| AR建模优化 | 1.3961 |
| GP+GA建模优化 | 1.1834 |
表选项
 |
| 图 4 GP+GA建模前后陀螺漂移角速度对比Fig. 4 Contrast of angular speed of gyroscope’s drift between before and after optimized by GP+GA |
| 图选项 |
4 结 论本文分析了陀螺仪的常用模型,针对陀螺仪量测噪声部分利用GP+GA方法对陀螺仪进一步建模分析,通过分析可知:1) 经过GP+GA建模,陀螺仪的方差降低了73.72%,与经典时间序列建模中的AR建模方法相比,精度提高了4.72%.2) 该建模方法和传统的时间序列建模方法相比可以更加有效地补偿陀螺仪的随机漂移误差,进而提高系统的稳定性.3) GP+GA算法在误差建模方面尤其是在非线性误差建模方面优势明显.
参考文献
| [1] | Li J L, Fang J C, Du M.Error analysis and gyro-bias calibration of analytic coarse alignment for airborne POS[J].IEEE Transactions on Instrumentation and Measurement, 2012, 61(11):3058-3064. |
| Click to display the text | |
| [2] | Hua Z W, Rui L C.Correlation coefficient stationary series method for gyroscope random drift[C]//Proceedings of 2011 6th IEEE Conference on Industrial Electronics and Applications.Piscataway, NJ:IEEE Press, 2011:2270-2273. |
| Click to display the text | |
| [3] | Sun H, Wu Q Z.Error analysis and algorithm implementation for an improved optical-electric tracking device based on MEMS[C]//International Symposium on Photoelectronic Detection and Imaging.Bellingham, WA:SPIE, 2013, 8907:1-7. |
| Click to display the text | |
| [4] | Li J L, Fang J C.Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system[J].IEEE Transactions on Instrumentation and Measurement, 2013, 62(1):210-220. |
| Click to display the text | |
| [5] | 王新龙, 李娜.MEMS陀螺随机误差的建模与分析[J].北京航空航天大学学报, 2012, 38(2):170-174. Wang X L, Li N.Error modeling and analysis for random drift of MEMS gyroscopes[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2):170-174(in Chinese). |
| Cited By in Cnki (4) | Click to display the text | |
| [6] | 杜红松, 程建华, 唐苗苗.基于ARMA的微惯性传感器随机误差建模方法[J].传感器与微系统, 2013, 32(4):54-64. Du H S, Cheng J H, Tang M M.Stochastic error modeling method for micro inertial sensor based on ARMA[J].Transducer and Microsystem Technologies, 2013, 32(4):54-64(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [7] | 钱华明, 夏全喜, 阙兴涛, 等.MEMS陀螺仪随机漂移仿真和试验[J].北京航空航天大学学报, 2010, 36(6):636-639. Qian H M, Xia Q X, Que X T, et al.Smiulation and expermient of random errors of MEMS gyroscope[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(6):636-639(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [8] | Li J L, Jiao F, Fang J C, et al.Temperature error modeling of RLG based on neural network optimized by PSO and regularization[J].IEEE Sensors Journal, 2014, 14(3):912-919. |
| Click to display the text | |
| [9] | Lin D Z, Yang Q H, Dong L L, et al.Analysis and compensation of MEMS gyroscope drift[C]//Proceedings of 2013 IEEE Seventh International Conference on Sensing Technology.Piscataway, NJ:IEEE Press, 2013:592-596. |
| Click to display the text | |
| [10] | Xia Y, Chen W J, Peng W H.Research on random drift modeling and a Kalman filter based on the differential signal of MEMS gyroscope[C]//25th Chinese Control and Decision Conference.Piscataway, NJ:IEEE Press, 2013:3233-3237. |
| Click to display the text | |
| [11] | Li Q, Xu J N.Random drift modeling for MEMS gyroscope based on lifting wavelet and wavelet neural network[C]//Proceedings of 2011 International Conference on IEEE Electric Information and Control Engineering.Piscataway, NJ:IEEE Press, 2011:3454-3456. |
| Click to display the text | |
| [12] | Urvesh B, Mark J, Zhang M J.Evolving diverse ensembles using genetic programming for classification with unbalanced data[J].IEEE Transactions on Evolutionary Computation, 2013, 17(3):368-386. |
| Click to display the text | |
| [13] | Lee Y-S, Tong L-I.Forecasting time series using a methodology based on autoregressive integrated moving average and genetic programming[J].Knowledge-Based Systems, 2011, 24(1):66-72. |
| Click to display the text | |
| [14] | Garg A, Tai K.Review of genetic programming in modeling of machining processes[C]//Proceedings of 2012 International Conference on Modelling, Identification and Control, ICMIC 2012.Piscataway, NJ:IEEE Press, 2012:653-658. |
| Click to display the text |
