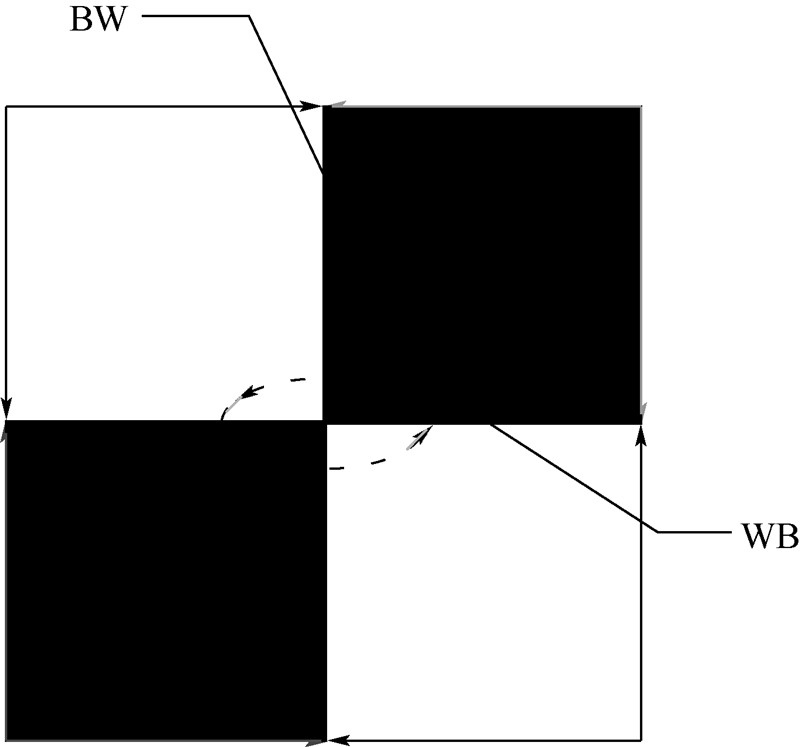
 |
| 图 1 X角点Fig. 1 X point |
| 图选项 |
① X角点是BW线和WB线的交点.② X标记点的方向可以用BW线和WB线的方向表示.③ X标记点的对称性.对其中的任意像素p,都能找到其关于X角点对称的像素,该像素与p同时位于黑块或白块.中心射影变换(或小孔成像)不保证正交性,但保证共线性质.因而在图像上,X标记点的图像在局部仍保持对称性.令BW线和WB线的像分别为lbw，lwb,交点X的像为x.2 基于对称性计算的X角点检测2.1 对称性计算与像素级位置确定在位于以候选角点为中心,边长为2r的正方形窗口上,提取像素组成首尾相连的像素段,如图 2(a)所示.将图 2(a)中的BW线和WB线与像素段的4个交点,按逆时针方向分别称为A，B，C，D台阶;令a，b，c，d分别表示折线AO1B，BO2C，CO3D，DO4A的长度.本文算法根据窗口的平行移动提取像素段,采样数据与X角点的具体方向无关.在待测试像素段上,像素的亮度在实际情况下如图 2(b)所示.设像素段由n个像素组成,记其中第i个像素为pi(i=1,2,…,n),f(pi)为pi的灰度值.由于同一区域内的像素在位置和灰度级上具有较强的一致性和相关性,不同区域内的像素存在照度不均匀、对比度不同的情况.为了保证较强的抗噪性能,并体现同一区域的整体情况,选择像素段的均值作为二值化阈值.为了降低噪声点对二值化阈值选取的影响,需先用滤波器对像素段进行预处理.通过对像素段内灰度值进行局部二值化,将pi的灰度值化为f′(pi).二值化后像素段内各个像素的灰度值如图 2(c)所示.
 |
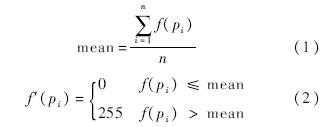
| 图 2 取像素段并确定台阶Fig. 2 Taking pixel segment and determining steps |
| 图选项 |
图 2(c)中的曲线反映X角点测试像素段内存在4处灰度值变化剧烈的点,即图 2(a)中介绍的A，B，C，D 4个台阶.通过对二值化后像素段内的相邻元素取差分Δ=f′(pi)－f′(pi－1)(i=1,2,…,n),判断Δ的绝对值是否为255,从而确定此像素段内是否存在4个台阶及它们在像素段内的像素级位置.然后求出a，b，c，d.根据X标记点图像特征中的对称性,可知对于当前窗口内的任意像素点p,若要在当前窗口内找到其关于窗口中心的对称点,4个台阶之间的距离a，b，c，d理论上应该相等.由此可得对称性计算的数学公式:
以图 2(a)中的每个像素为窗口中心计算对应的SC值,其结果如图 3所示.图中x，y坐标表示像素点的二维位置,z坐标表示对应的对称性计算值.可知,窗口中心越接近X角点,其对称性计算值SC越小.所以当SC取得局部最小值时,即可确定当前窗口中心为角点位置.
 |
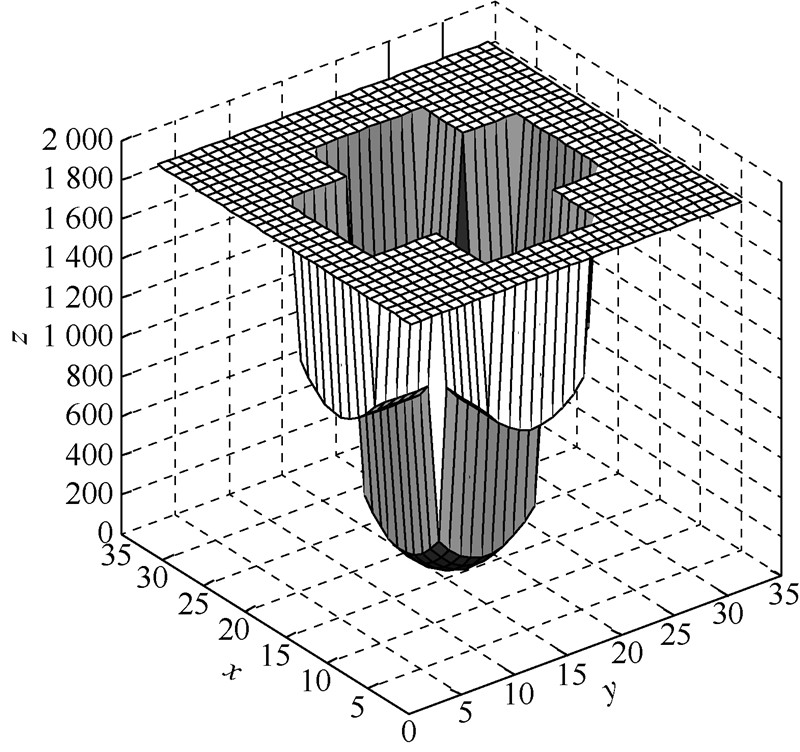| 图 3 图 2(a)对称性计算结果Fig. 3 Result of symmetry calculation of Fig. 2(a) |
| 图选项 |
2.2 角点的亚像素位置计算及方向确定通过对称性搜索得到X角点及其对应台阶的像素级位置,为求解其亚像素级位置,采用二次曲线拟合法[20]先求此X角点4个台阶的一维亚像素位置A′,B′,C′,D′,然后利用边缘直线相交确定角点的亚像素位置.在已知台阶像素位置的前提下,只选取台阶邻近点进行二次曲线拟合可以减少计算量,避免无用点影响拟合结果.选取以台阶(假设为台阶A)为中心的5个点进行二次曲线拟合.拟合点的亮度及相邻点亮度差(梯度)如图 4(a)和图 4(b)所示.将离散的梯度值拟合为一条连续的曲线,近似为二次抛物线,如图 4(b)所示.二次抛物线的极值点即为沿该梯度方向灰度变化最大的地方,即为台阶的准确位置.
 |
| 图 4 一维边缘模型Fig. 4 Model of one-dimensional edge |
| 图选项 |
一个角点q(x,y)周围存在4个台阶,所以要进行4次曲线拟合,分别得到4个台阶在像素段内的一维亚像素位置A′,B′,C′,D′.因所得台阶存在于以角点像素位置为中心的边长为2r的正方形窗口上,即可利用此对应关系求出其二维的亚像素位置.假设某台阶的一维位置为m,根据m值所在范围可得其对应二维坐标为
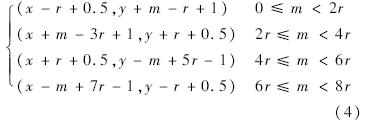
将台阶的一维位置转至与图像相对应的二维位置时,由于其在垂直或水平方向上与候选角点的像素距离为r,所以可以通过增减r确定在此方向上的像素位置,但实际上边缘的位置存在于像素内的任何位置,为了减小在此方向上的误差,所以增加0.5个像素的偏移.一维和二维空间对应关系如图 5所示,图中r=5.据此可求得4个台阶的二维亚像素位置A″，B″，C″，D″.
 |
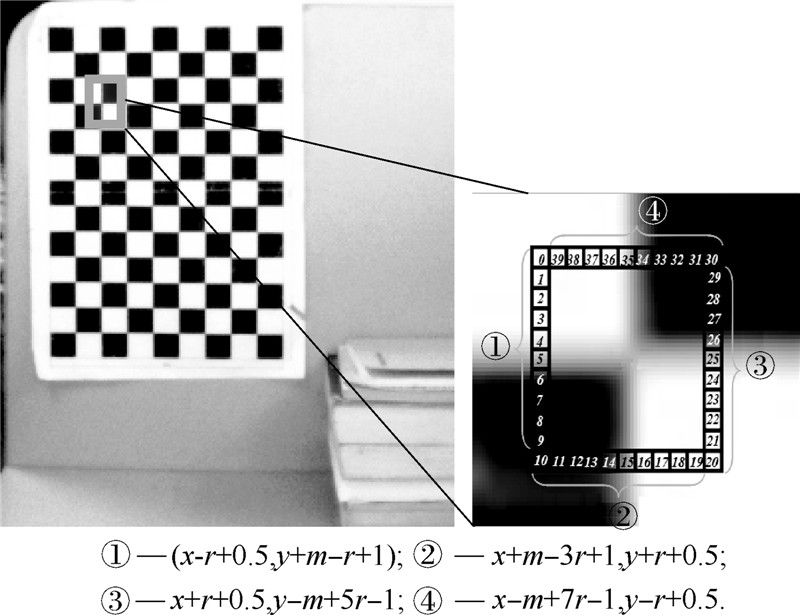| 图 5 一维与二维空间对应关系Fig. 5 Relationship between one- and two-dimensional spaces |
| 图选项 |
由影射几何可知,X角点的亚像素位置为
式中
其中,
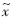为x的齐次坐标表示;lbw,lwb为直线在图像上的齐次坐标；
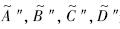是A″，B″，C″，D″的图像齐次坐标.在介绍X标记点的图像特征时曾说到X标记点的方向信息可以用BW线和WB线的方向表示,即lbw与lwb的方向.通过求lwb，lbw与水平方向的夹角θ1，θ2来存储角点的方向信息，X角点的方向如图 6所示. |
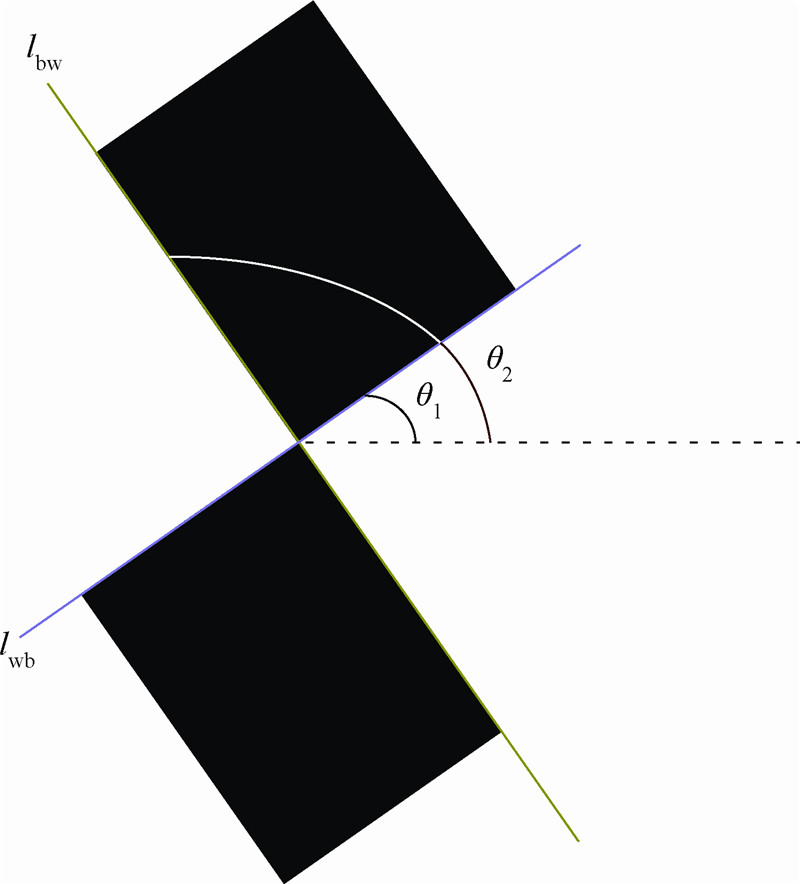| 图 6 X角点的方向Fig. 6 Direction of X-corner point |
| 图选项 |
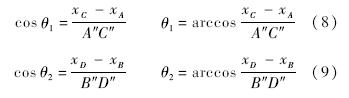
3 角点定位实验及分析为了对第2节阐述的基于对称性计算的X角点检测方法进行验证,利用Visual Studio 2008和Matlab 7.11对算法进行了编程实现.实验分为2部分:第1部分是已知各个角点理论位置及角点真实方向信息的仿真实验,通过该部分实验能较便捷精确地检验算子的精确度、抗噪性能和抗畸变性能,同时在该部分实验中使用了经典Harris算法和本文算法对相同实验图像进行对比分析.第2部分是物理实验,使用双目摄像机BumbleBee2 BB2-08S2C,在不同环境下采集实验图像,图像尺寸大小为1 024×768像素.由于不知道角点在实时采集图像中的理论位置,所以在物理实验中通过与Micron Tracker系统及Harris算法进行对比来分析SC算子的性能.Micron Tracker系统由Claron Tech公司生产,其被广泛应用于众多需要进行精确定位的场合.文献[7]指出其测量精度达到0.2 mm.实验中用圆圈标记X角点,分别用短线和长线标识lwb与lbw，如图 7所示.
 |
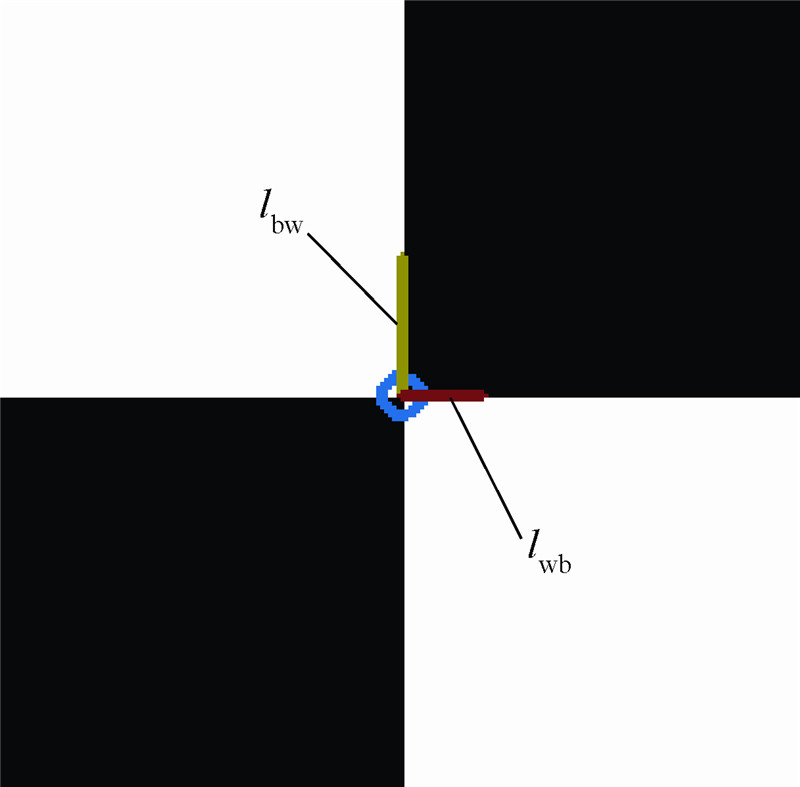| 图 7 X角点及其方向标识Fig. 7 X-corner point and its direction detected by SC detector |
| 图选项 |
3.1 仿真实验为验证噪声和畸变对本文算法性能的影响,选择畸变后的仿真图像进行角点定位实验.首先利用Matlab软件对含有25个X角点的棋盘格图案进行仿射变换,得到图片仿射后各个角点的理论位置
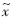i(i=1,2,…，25)及相应lwb,lbw与水平方向的夹角
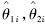对仿射后的图像加入标准差为δ的高斯噪声生成噪声图像,然后采用SC算子和集成到OpenCV中的Harris算子分别进行角点定位,记定位结果为xi(i=1,2,…，25),记SC算子求得的lwb与lbw的角度分别为θ1i,θ2i.然后将畸变噪声图像的检测结果与理论值进行比较,分析噪声和畸变对算法定位和定向精度的影响,由于Harris算法不能提供角点的方向信息,所以只列出SC算子的定向结果及分析.定义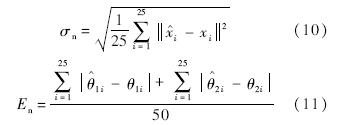 
式中,σn和En分别为定位和定向误差.仿真实验结果如表 1所示,图 8为噪声标准差δ=0.24时的畸变图像定位结果.表 1 仿真实验结果 Table 1 Results of simulation experiments
| 参数 | 算子 | 噪声标准差δ | ||||||
| 0.04 | 0.08 | 0.12 | 0.16 | 0.20 | 0.24 | 0.28 | ||
| σn/像素 | ||||||||
| SC算子 | 0.329 3 | 0.329 3 | 0.355 3 | 0.354 4 | 0.432 0 | 0.420 0 | 0.421 8 | |
| Harris | 0.305 4 | 0.321 0 | 0.338 7 | 0.362 2 | 0.378 0 | 0.413 2 | ||
| En/(°) | SC算子 | 1.538 4 | 1.468 8 | 1.481 2 | 1.424 4 | 1.481 2 | 1.764 0 | 1.876 4 |
表选项
 |
| 图 8 噪声标准差δ=0.24时的畸变图像定位结果Fig. 8 Result of distortion image when noise standard deviation is 0.24 |
| 图选项 |
SC算子和Harris算子的定位精度都会随图像噪声的加强而有所下降,当噪声标准差小于0.28时,SC算子和Harris算子的定位误差都在0.5个像素以内.两者在定位精度方面不相上下,但是Harris易受噪声的影响,误检点较多,在实际应用中会产生不必要的干扰,如图 8(b)所示.在噪声标准差为0.28时,因Harris算子误检点过多,以致无法计算精确度.而SC算子则表现出良好的抗噪性和抗畸变性.同时,由表 1可以看出,当噪声标准差小于0.28时,SC算子的定向精度也很稳定,平均误差在2°以内,稳定精确的定向功能也是SC算子的一个优势.总体来说,本文提出的算法能在保证基本不受噪声和畸变影响的同时进行精确定位及定向,满足应用中对鲁棒性能及精度的要求.3.2 物理实验物理实验分为3部分:第1部分是与Harris算法及Micron Tracker系统的定性比较实验;第2部分是检验光照亮度对算法性能影响的实验;第3部分是与Micron Tracker系统的定量比较实验.表 2 SC算子、Harris算子与Micron Tracker系统检测结果对比Table 2 Comparison between experimental results of SC detector,Harris detector and Micron Tracker system
| 实际角点数 | SC算子 | Harris | Micron Tracker | ||||
| X角点 | 非X角点 | X角点 | 非X角点 | X角点 | 非X角点 | ||
| 第1组 | 96 | 96 | 0 | 96 | 310 | 44 | 0 |
| 第2组 | 136 | 136 | 0 | 136 | 371 | 71 | 0 |
| 第3组 | 136 | 136 | 0 | 136 | 363 | 85 | 0 |
| 第4组 | 136 | 136 | 0 | 136 | 357 | 69 | 0 |
表选项
第1部分的对比实验分为4组,统计结果在表 2中给出.第1组实验里放置的棋盘图案有96个X角点,黑白块的边长为20 mm,放置在距相机1 m远的地方.第2组实验里增加了一黑白块边长为30 mm,角点个数为40的棋盘格.第3组实验时,改变第2个棋盘格平面与相机平面之间的夹角.第4组实验中将第2个棋盘格进行旋转并改变2个棋盘格与相机平面之间的夹角.图 9给出了第4组棋盘格实验的结果图.由实验结果看出,Harris算法的检测结果中存在很多误检点,而Micron Tracker系统不太稳定,容易出现漏检的情况.与它们相比,本文提出的SC算子在保证基本排除非X角点的前提下全部检出了X角点.
 |
| 图 9 棋盘格实验Fig. 9 Experiments of X-corner points |
| 图选项 |
图 10显示了在不同光照亮度下SC算子的检测情况.光照亮度从高亮度到正常再到低亮度,都没有影响SC算子对X角点及其方向的检测.图中分别用短线和长线标出了WB线和BW线的方向.实验表明本文提出的算法对亮度改变具有一定的鲁棒性.
 |
| 图 10 不同光照亮度下SC算子的检测结果Fig. 10 Results of SC detector under different light conditions |
| 图选项 |
上述2部分物理实验对角点检测算法的抗噪性、抗畸变性以及对光照变化的鲁棒性做了一个定性的分析.下面通过与Micron Tracker系统的对比实验定量地分析角点检测算法的误检率、漏检率和检测精确度.实验所用图像中包括96个X角点的棋盘格图案,黑白块边长为20 mm;距离相机1 m远.为比较角点定位精度,在利用生产该摄像机的Claron Tech公司提供的源代码对其提取的左视图进行角点检测后,将导出的左视图置于SC算子中进行检测.为比较2个算法在不同条件下的检测结果,还改变了棋盘格平面和摄像机平面之间的角度.图 11所示为30°时,与Micron Tracker系统的对比实验的情形.表 3中的数据是20组实验结果的平均值.其中正检率=正确检测的角点数/实际总角点数,漏检率=漏检的角点数/实际总角点数,误检率=误检的角点数/实际总角点数.数据显示当棋盘格平面和摄像机平面之间的夹角较小时,Micron Tracker系统的漏检率较高,SC算子则几乎不存在漏检,随着角度的增加,Micron Tracker系统漏检率逐渐降低,正检率逐渐升高.SC算子则相反,当被测平面过于倾斜时,由于检测窗口的大小r不适合该情况,正检率会有所下降,出现漏检.2个算法的误检率则一直都很低,总的来说都具有较好的鲁棒性.对于更普遍的接近平行的情况,SC算法则在稳定性方面更有优势.
 |
| 图 11 与Micron Tracker系统的对比实验Fig. 11 Comparative experiments with Micron Tracker |
| 图选项 |
表 3 不同角度下Micron Tracker系统与SC算子的检测结果Table 3 Results of Micron Tracker system and SC detector under different conditions
| 夹角/(°) | Micron Tracker | SC算子 | ||||
| 正检率/% | 漏检率/% | 误检率/% | 正检率/% | 漏检率/% | 误检率/% | |
| 0 | 31.25 | 68.75 | 0 | 100 | 0 | 0 |
| 30 | 98.05 | 1.95 | 0 | 100 | 0 | 0 |
| 60 | 99.22 | 0.78 | 0.52 | 69.53 | 30.47 | 0.65 |
表选项
通过对20组实验的检测结果进行统计分析,获得2个算法的检测结果分别在x，y方向上测量差的标准差(σs)、均方根(RMS,σr)及2个结果间距离的标准差和RMS.Micron Tracker系统与SC算子检测结果间的关系如表 4所示.可以看出2个算法在精度上是不相上下的.表 4 Micron Tracker系统与SC算子检测结果间的关系Table 4 Relations between the two detectors’ test results
| 像素 | |||||
| Δx=x′－x | Δy=y′－y |  | |||
| 标准差(σs) | RMS(σr) | 标准差(σs) | RMS(σr) | 标准差(σs) | RMS(σr) |
| 0.174 3 | 0.191 7 | 0.164 7 | 0.180 2 | 0.110 9 | 0.263 1 |
| 注：x′—Micron Tracker系统的检测结果;x—SC算子的检测结果. | |||||
表选项
当计算Δx,Δy或距离Dis的标准差和RMS时,分别用它们代替式(12)和式(13)中的z进行计算.与Micron Tracker系统的对比实验表明SC算子与其有相同的检测精度,满足精确定位的要求.在Intel Core i3 CPU 3.3 GHz RAM 2.0 GB的处理器上,检测一帧大小为1 024×768包含96个角点的棋盘格图像,本文算法一般需要0.187 s,Harris算法与Micron Tracker系统平均花费时间则分别为0.053 s,0.069 s.传统的Harris算法并不满足实时性要求[9, 21],因本文使用的是OpenCV中已优化的Harris,所以速度快.而Micron Tracker系统封闭,不做讨论.本文SC算子因需要利用式(3)对图像中的每个像素点计算对应的SC值,所以耗时相对较大,但在实际工程项目中,若采用适当的优化加速算法,还能大大降低本文算法的处理时间.4 讨论及分析实验发现,本文算法会因窗口大小r选取不当导致漏检,通过实验总结和分析,利用自适应法根据图片的大小及实验条件自动调节窗口的大小,以求降低漏检率.如果出现误检,则主要是因为窗口内检测到如下2种干扰情况,它们与X角点一样存在4个台阶,但是窗口内并无交点.通过对X角点和干扰情况进行分析,可以用下列条件对干扰情况进行排除:1) 若当前窗口中心的邻域内像素灰度值为黑白混合,则为X角点,若为纯黑或纯白,则为干扰情况.2) 根据前面对A,B,C,D的定义,标出各干扰情况中的A,B,C,D,如图 12所示.取AC或BD上的像素点,若其邻域内像素灰度值为黑白混合,则为X角点,否则为干扰.
 |
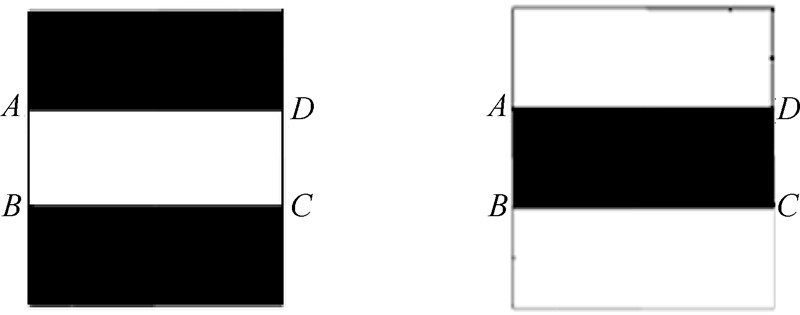| 图 12 干扰图形Fig. 12 Interferences |
| 图选项 |
对这些干扰情况进行排除,能大大降低误检率.5 结 论分析了X角点的图像特征,提出了基于对称性计算的X角点检测算法.该方法具有以下特点:1) 仅提取X角点,排除了其他类型的角点,为特征识别提供亚像素级的定位信息和准确的定向信息.2) 能有效排除非X角点的干扰.本文算法虽然在亚像素定位精度方面与其他2种经典算法相当,但在图像发生畸变并有较高噪声的情况下,本文算法仍能在基本排除非X角点的同时准确提取X角点的位置信息,并且还能提供较高精度的方向信息,在位姿测量及模板匹配中具有较高的应用价值.
参考文献
| [1] | Sánchez-Margallo J A, Sánchez-Margallo F M,Pagador J B,et al.Technical evaluation of a third generation optical pose tracker for motion analysis and image-guided surgery[M]//Clinical Image-Based Procedures.From Planning to Intervention.Heidelberg:Springer,2013:75-82. |
| [2] | 王志衡,吴福朝, 王旭光.基于局部方向分布的角点检测及亚像素定位[J].软件学报,2008,19(11):2932-2942. Wang Z H,Wu F C,Wang X G.Corner detection and sub-pixel localization based on local orientation distribution[J].Journal of Software,2008,19(11):2932-2942(in Chinese). |
| Cited By in Cnki (26) | |
| [3] | Zhang Z Y. A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334. |
| Click to display the text | |
| [4] | 刘阳成,朱枫. 一种新的棋盘格图像角点检测算法[J].中国图象图形学报,2006,11(5):656-660. Liu Y C,Zhu F.A new algorithm for X-corner detection[J].Journal of Image and Graphics,2006,11(5):656-660(in Chinese) |
| Cited By in Cnki (69) | |
| [5] | Bouguet J Y. Camera calibration toolbox for matlab[EB/OL].California,Tex:California Institute of Technology,2009 (2013-12-02).http://www.vision.caltech.edu/bouguetj/calib_doc/. |
| Click to display the text | |
| [6] | Bradski G, Kaehler A.Learning OpenCV:computer vision with the OpenCV library[M].Sebastopol:O'Reilly Media,Inc.,2008:422-430. |
| [7] | Claron Technology Inc. Micron tracker developer's manual MTC 3.6[M].Toronto:Claron Technology Inc.,2011:25-35. |
| [8] | Harris C, Stephens M.A combined corner and edge detector[C]//Proceedings of Alvey Vision Conference.Manchester:Organising Committee AVC 88,1988,15:147-152. |
| Click to display the text | |
| [9] | 王崴,唐一平, 任娟莉,等.一种改进的Harris角点提取算法[J].光学精密工程,2008,16(10):1995-2001. Wang W,Tang Y P,Ren J L,et al.An improved algorithm for Harris corner detection[J].Optics and Precision Engineering,2008,16(10):1995-2001(in Chinese). |
| Cited By in Cnki (111) | |
| [10] | 侯建辉,林意. 自适应的Harris棋盘格角点检测算法[J].计算机工程与设计,2009,30(20):4741-4743. Hou J H,Lin Y.Adaptive Harris X-corner detection algorithm[J].Computer Engineering and Design,2009,30(20):4741-4743(in Chinese). |
| Cited By in Cnki (30) | |
| [11] | 郝颖明,朱枫. 摄像机在线标定中的棋盘格角点自动检测方法[J].计算机工程,2007,33(17):213-215. Hao Y M,Zhu F.Automatic X-corners detection for online camera calibration[J].Computer Engineering,2007,33(17):213-215(in Chinese). |
| Cited By in Cnki (15) | |
| [12] | 储珺,郭卢安政, 赵贵花.采用环形模板的棋盘格角点检测[J].光学精密工程,2013,21(1):189-196. Chu J,Guo L A Z,Zhao G H.Chessboard corner detection based on circular template[J].Optics and Precision Engineering,2013,21(1):189-196(in Chinese). |
| Cited By in Cnki (8) | |
| [13] | 胡海峰,侯晓微. 一种自动检测棋盘角点的新算法[J].计算机工程,2004,30(14):19-21. Hu H F,Hou X W.A new algorithm for automatically detecting chessboard corners[J].Computer Engineering,2004,30(14):19-21(in Chinese). |
| Cited By in Cnki (39) | |
| [14] | Chen D, Zhang G J.A new sub-pixel detector for X-corners in camera calibration targets[J].WSCG (Short Papers),2005,5:97-100. |
| Click to display the text | |
| [15] | 张广军. 视觉测量[M].北京:科学出版社,2008:57-61. Zhang G J.Vision measurement[M].Beijing:Science Press,2008:57-61(in Chinese). |
| [16] | 魏军,刘达, 王田苗,等.基于段测试的X角点检测与亚像素定位[J].机器人,2011,33(1):97-101. Wei J,Liu D,Wang T M,et al.Segment test based X comer detection and sub-pixel localization[J].Robot,2011,33(1):97-101(in Chinese). |
| Cited By in Cnki (5) | |
| [17] | Rosten E, Porter R,Drummond T.Faster and better:a machine learning approach to corner detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1):105- 119. |
| Click to display the text | |
| [18] | Lowe D G. Distinctive image features from scale-invariant key points[J].International Journal of Computer Vision,2004,60(2): 91-110. |
| Click to display the text | |
| [19] | Bay H, Tuytelaars T,Van Gool L.Surf:speeded up robust features[C]//Proceedings of the European Conference on Computer Vision.Heidelberg:Springer,2006:404-417. |
| Click to display the text | |
| [20] | 尚雅层,陈静, 田军委.高斯拟合亚像素边缘检测算法[J].计算机应用,2011,31(1):179-181. Shan Y C,Chen J,Tian J W.Sub-pixel edge detection algorithm based on Gauss[J].Journal of Computer Applications,2011,31(1): 179-181(in Chinese). |
| Cited By in Cnki (32) | |
| [21] | 郭永芳,于明, 孙以材.一种改进的快速角点检测方法研究[J].计算机工程与应用,2011,47(12):159-161. Guo Y F,Yu M,Sun Y C.Study on advanced rapid corner detection method[J].Computer Engineering and Application,2011,47(12):159-161(in Chinese). |
| Cited By in Cnki (16) |
