1 精加工模型在实际应用中,数控加工大致可分为粗加工、精加工和清根加工3个阶段.精加工的最终目的是保证零件的尺寸精度满足设计要求.精加工对曲面加工精度和表面质量要求均较高,因此,待加工模型的光滑极限曲面作为参考模型较为理想.在利用控制网格多次Loop细分得到极限曲面时,三角片以指数倍增长的问题非常突出.因此,本文直接将待加工模型的控制网格顶点由其对应的极限位置替代,以减少每次所需处理的三角片数据量.事实上,大多数情况下这种极限网格比控制网格逼近极限曲面的效果更好[13].自由曲面模型在精加工阶段主要有两个离散过程[7],其一是将连续的几何设计模型离散为精加工模型时产生的弦长误差;其二是精加工模型离散为一系列刀具轨迹时产生的残留高度误差.Loop极限曲面由极限网格逼近的过程,即为几何设计模型离散为精加工模型的过程.故定义弦长误差为极限网格的三角片与其所对应的极限曲面片之间的误差.通过不断Loop细分极限网格就可以得到满足弦长误差的精加工模型.自适应细分模式可以有效地减缓细分中数据量增长过快的问题,节省存储资源并提高绘制速度.因此,本文取三角片的弦长误差作为自适应Loop细分阈值,通过自适应插值Loop细分得到精加工模型.给定弦长误差c,具体步骤如下:\步骤1 计算网格M0每一个三角片的弦长误差,找到最小的一个弦长误差记为cmin.步骤2 不断Loop细分网格M0,直到细分i次后其最小弦长误差cmin<c,表明此时的网格Mi不需要均匀细分,并标记所有的三角片Fij为false,j=1,2,…,max F{Mi}.步骤3 对于任一个三角片Fij,如果其弦长误差cij>c,标记该三角片为true.步骤4 对标记为true的三角片进行插值Loop细分[14],如果细分后三角片Fji+1的弦长误差ci+1j<c,标记细分后的三角片为false.步骤5 重复步骤4直到所有三角片为false;消除存在裂缝的三角形并利用Loop极限位置更新细分曲面的顶点,输出精加工模型M.如果一个网格面已经停止细分,而其周围相邻面却未满足停止细分的准则,此时在相邻边处会产生缝隙.为了避免视觉上的漏洞,同时也为了保持新网格的二维流形性质,需要消除不同分辨率层网格面间的裂缝[15].
2 等残留高度精加工刀具轨迹2.1 等残留高度误差残留高度H是由走刀行距L决定的,如图 1给出走刀行距与残留高度之间的关系.假设球头刀的半径是R,则有
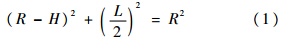
由式(1)可以推出:
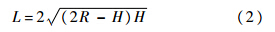
在精加工阶段,理想的情况是均匀的残留高度,即走刀行距L是常量,等残留高度会最大限度地减少刀具轨迹并且得到最短的加工时间.但是,等残留高度的计算复杂度较高,并且如果走刀行距L是常数,自由曲面模型不同的斜率会导致走刀步长s变化较大.如果把走刀步长s设为常量,会导致加工后的残留高度不均匀,甚至出现零件表面残留高度大于指定的误差,影响零件的加工精度.一个比较合理的方案就是把一个曲面分解为不同的区域,例如平坦和非平坦区域,然后采用不同的刀具轨迹规划.这样,既可以控制残留高度误差又可以减少多余的刀具轨迹.
 |
| 图 1 走刀行距L与残留高度H之间的关系Fig. 1 Relationship between step-over L and cusp height H |
| 图选项 |
基于上述讨论,目前需要解决的主要问题是分割精加工模型,并对分割后的模型进行不同的刀轨规划.由于参数曲面的几何性,分割参数曲面计算复杂不易做到.但是,对于多面体网格模型而言,分割模型相对较容易完成[16].本文提出一种等斜率跟踪法来分割精加工模型.给定倾斜角阈值θ,如图 2所示.等斜率曲线就是由曲面上那些斜率为常数θ的点组成.如果是闭合模型,那么等斜率曲线亦为闭合曲线环.对于精加工模型上的任意顶点vi,其单位法向量为Ni(nx,ny,nz).假设顶点vi在极限曲面上的倾斜角为α,那么nz=cos α.所以,寻找精加工模型上等斜率曲线就是寻找所有的点具有相同的nz,即具有相同的倾斜角.对于精加工模型M,等斜率曲线可以通过三角片的边vivj与等斜率曲线相交得到.该边须满足:nzi≤cos θ≤nzj或者nzi≥cos θ≥nzj.这里nzi是顶点vi的法向量z轴坐标的分量,nzj是顶点vj的法向量z轴坐标的分量.通过线性插值vi和vj得到该曲面与等斜率曲线的相交点后,精加工模型即可以分割为平坦和非平坦区域.算法具体步骤如下:
 |
| 图 2 曲面倾斜角度对残留高度的影响Fig. 2 Slope angle of surface and cusp height |
| 图选项 |
步骤1 对于精加工模型M的每一个三角片vivjvk,计算其3个顶点的法向量z轴坐标分量.如果其法向量z轴坐标分量都小于cos θ,标记该三角片为平坦;如果其法向量z轴坐标分量都大于cos θ,标记该三角片为非平坦.剩余的三角片为相交的三角面,标记为不可访问的面.步骤2 从标记为相交的三角片开始,利用线性插值找到等斜率曲线的第一个点,标记该面为可访问;下一个标记为相交的三角片与该三角片共享同一条边.找到下一个相交的等斜率点并标记该面为可访问.继续搜寻直到回到第一个相交点,此时产生一条等斜率曲线环.步骤3 继续搜寻标记为不可访问的面,按照步骤2生成另一条等斜率曲线环.步骤4 不断执行步骤3直到所有相交的三角片都为可访问为止.上述算法利用了Loop细分曲面三角片之间的拓扑关系来简化等斜率曲线的跟踪,其计算复杂度为O(n),其中n是精加工模型三角片的个数.这里,定义平坦和非平坦区域的交线,即等斜率曲线环,属于平坦或者非平坦区域两者之一.如此一来,模型被分割为两个完全不同的区域.需要指出的是,上述算法分割曲面所得到的区域不仅仅只有平坦和非平坦区域,实际上为两个以上不同的区域.为了避免过多的抬刀和空切,所分解出的区域的个数亦不能太多.对于给定的倾斜角阈值θ,可以首先给出估计值.例如,限制最短的加工时间所得到的阈值,或者根据经验不断测试得到的阈值.图 3是利用等斜率跟踪法对于圆盘模型进行分割的实例.可以看出,给定不同的倾斜角阈值所得到的分割曲面亦不相同.图 4是分割bishop模型的实例.其中,倾斜角阈值分别为45°和80°.当阈值为45°和80°时,bishop的正面都被分割为4个等斜率曲线环,即4个不同的区域.很明显,当阈值为80°时所分割的4个区域更为合理.
 |
| 图 3 等斜率跟踪法分割圆盘模型Fig. 3 Iso-slope curve tracing method for disc model decomposition |
| 图选项 |
 |
| 图 4 等斜率跟踪法分割bishop模型Fig. 4 Iso-slope curve tracing method for bishop model decomposition |
| 图选项 |
等斜率分割算法对于大数据量的细分曲面加工非常有利.随着细分次数的递增,细分曲面数据量增长过快,此时依照等斜率跟踪法可以将精加工模型分割为不同的区域.对于非平坦区域应用等高线法生成刀轨,对于平坦区域应用截面法生成刀轨,进而得到相对均匀残留高度的刀轨.
2.2 无过切刀具轨迹计算多面体网格模型精确和完整的等距面比较复杂[17].本文采用等距精加工模型的每个顶点来逼近等距面.利用等距面生成刀位点时会产生自相交从而导致零件过切.在3D模型中较难检测和解决自相交问题,故选择转化为2D刀具轨迹之后进行处理.对于等高线法生成的刀具轨迹,存在两种类型的自相交:局部自交和全局自交.局部自交是与其中一条等高线有交点,全局自交是与很多条等高线有多个交点.对于自相交,有如下两种方法可以解决:①等高线法.利用等高线走向,开始于一个有效的点并且沿着一个方向寻找最简单的多边形等高线.②多边形裁剪法.标记在等高线内部的边,并且去除它们形成最终的等高线环.对于截面法生成刀具轨迹产生的过切问题,三轴数控加工中可以利用扫描线法来寻找自相交点[18].通过检测自相交点去除无效部分保留剩余刀轨.
3 精加工刀具轨迹生成实例为了检验基于Loop细分曲面的精加工刀具轨迹生成算法的有效性,结合OpenGL在Visual C++6.0下实现本文算法.对于图 5(a)的knob模型而言,首先利用算法自适应插值Loop细分生成精加工模型,弦长误差为0.002.当倾斜角阈值为50.4°时(如图 5(b)),knob模型所分割的平坦区域和非平坦区域如图 5(c)和图 5(d)所示.利用等高线法生成全局刀轨,然后对于残留高度较大的平坦区域利用截面法生成精加工刀具轨迹,如图 5(e)所示.由图 5(f)的精加工仿真结果可以看出,对于knob模型不同的斜率采取走刀变步长以保持均匀残留高度.
 |
| 图 5 knob模型精加工刀具轨迹生成Fig. 5 Tool path generation for knob model finish machining |
| 图选项 |
图 6(a)是运用自适应插值Loop细分生成的face模型精加工模型,弦长误差为0.05.利用等斜率跟踪法将精加工模型分割后的模型如图 6(b)所示,倾斜角阈值为14°.在非平坦区域运用等高线法生成刀具轨迹,对于平坦区域运用截面法生成刀具轨迹,如图 6(d)所示.图 6(e)是最终的相对均匀等残留高度的加工仿真结果.
 |
| 图 6 face模型精加工刀具轨迹生成Fig. 6 Tool path generation for finish machining of human face surface model |
| 图选项 |
为验证本文算法的可行性,以face模型为例进行铣削加工.实验机床为VMC0850B三轴立式加工中心.工件材料为铝合金7075,毛坯尺寸为120 mm×100 mm×30 mm.实验刀具为Sandvik硬质合金球头刀.在本实验的精加工刀具路径规划中,对于非平坦区域(鼻尖、嘴处)采用等残留高度法;对于平坦区域(额头、脸处)采用截面法生成刀具轨迹.精加工的切削参数见表 1.
表 1 切削参数Table 1 Cutting parameters
| 参数 | 刀具直径/mm | 刀齿数 | 主轴转速/(r·min-1) | 进给速度(mm·min-1) | 行距/mm | 切削余量/mm |
| 数值 | 8 | 2 | 4 000 | 900 | 0.04 | 0.25 |
表选项
三轴铣削加工过程如图 7(a)所示;非平坦区域运用等高线法加工后的结果如图 7(b)所示,可以清晰地看出face模型被分割为非平坦区域和平坦区域;图 7(c)是精加工后零件的正面图.由于本文重点讨论的是Loop细分曲面在精加工中刀具轨迹的生成,并未进行清根加工,所以精加工表面质量不够光滑.此外,由于是三轴铣削加工,无法加工face模型鼻孔凹陷处,利用多轴加工规划Loop细分曲面刀具轨迹将是未来的研究方向.
 |
| 图 7 face模型精加工实例Fig. 7 Result of finish machining of human face surface model |
| 图选项 |
4 结 论本文重点探讨了Loop细分曲面在精加工阶段刀具轨迹生成算法.1) 针对精加工模型,通过自适应插值Loop细分算法来控制几何模型离散为精加工模型时所产生的弦长误差.该算法在满足弦长误差的同时可以有效减缓Loop细分中三角片指数级增长的问题.2) 由于精加工模型离散为一系列刀具轨迹时,零件表面残留高度过大会影响零件的加工精度.因此,本文提出等斜率跟踪法将精加工模型分解为平坦和非平坦区域,对于平坦区域应用截面法生成刀具轨迹,对于非平坦区域应用等高线法生成刀具轨迹.该算法不仅在处理大数据量Loop细分曲面精加工方面具有优势,又能够得到整张曲面相对均匀残留高度的刀具轨迹.3) 最后以face模型为例对上述算法进行了三轴铣削加工实验验证.后续将研究基于Loop细分曲面的多轴数控加工刀具轨迹生成.
参考文献
| [1] | 周济,周艳红. 数控加工技术[M].北京:国防工业出版社,2002:78-147. Zhou J,Zhou Y H.Numerical control machining technology[M].Beijing:National Defence Industry Press,2002:78-147(in Chinese). |
| [2] | Kurgano J, Suziki H K F.Generation of NC tool path for subdivision surfaces[C]//Proceedings of CAD/Graphics.Kunming:IEEE Computer Society Press,2001:676-682. |
| [3] | 钟大平,周来水, 王占东,等.细分曲面的NC导轨生成算法及实现[J].东南大学学报,2004,34(1):1-4. Zhong D P,Zhou L S,Wang Z D,et al.Research on NC tool path generation for subdivision surface[J].Journal of Southeast University,2004,34(1):1-4(in Chinese). |
| Cited By in Cnki (145) | |
| [4] | 白杰,赵罡, 姚福生.带折痕的Loop细分曲面等距面处理算法[J].计算机辅助设计与图形学学报,2008,20(10):1261-1265. Bai J,Zhao G,Yao F S.An offset algorithm for Loop subdivision surface with creases[J].Journal of Computer-Aided Design & Computer Graphics,2008,20(10):1261-1265(in Chinese). |
| Cited By in Cnki (136) | |
| [5] | 赵建民. 基于Catmull-Clark模式的细分曲面NC刀具轨迹生成技术[D].大连:大连理工大学,2008. Zhao J M.Technology of generating NC tool path for subdivision surfaces based on Catmull-Clark scheme[D].Dalian:Dalian University of Technology,2008(in Chinese). |
| Cited By in Cnki (110) | |
| [6] | 唐虹. Catmull-Clark细分曲面的NC刀具生成关键技术研究[D].南京:南京航空航天大学,2008. Tang H.Research on key technologies of NC tool path generation based on Catmull-Clark subdivision surface[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2008(in Chinese). |
| Cited By in Cnki (88) | |
| [7] | Lu C, Ting K.Subdivision surface-based finish machining[J].International Journal of Production Research,2006,44(12):2445-2463. |
| Click to display the text | |
| [8] | 孙殿柱,范述鑫, 李延瑞,等.三角网格细分曲面数控加工刀轨快速生成算法[J].农业机械学报,2009,40(3):218-221. Sun D Z,Fan S X,Li Y R,et al.Algorithm of NC tool path generation for triangular meshing[J].Journal of Agricultural Machinery,2009,40(3):218-221(in Chinese). |
| Cited By in Cnki (198) | |
| [9] | Yuan N T, Liao W H,Tang H.Generation of NC tool path for Catmull-Clark subdivision surface[C]//Proceeding of First International Conference on Modeling and Simulation.Nanjing:IEEE Computer Society Press,2008:93-98. |
| [10] | 徐金亭,刘伟军, 卞宏友,等.基于网格曲面模型的等残留刀位轨迹生成方法[J].机械工程学报,2010,46(11):193-198. Xu J T,Liu W J,Bian H Y,et al.Constant scallop tool path for triangular surface machining[J].Journal of Mechanical Engineering,2010,46(11):193-198(in Chinese). |
| Cited By in Cnki (267) | |
| [11] | 戴军富,秦开怀. Doo-Sabin曲面NC刀具的并行轨迹计算[J].计算机辅助设计与图形学学报,2003,15(5):604-609. Dai J F,Qin K H.A parallel method for generating NC tool paths of Doo-Sabin surfaces[J].Journal of Computer-Aided Design & Computer Graphics,2003,15(5):604-609(in Chinese). |
| Cited By in Cnki (75) | |
| [12] | 陆云芳. 细分曲面在CAM中的关键技术研究[D].杭州:浙江大学,2007. Lu Y F.Research on the key technology of subdivision surface in CAM[D].Hangzhou:Zhejiang University,2007(in Chinese). |
| Cited By in Cnki (198) | |
| [13] | Huang Z J, Wang G P.Bounding the distance between a Loop subdivision surface and its limit mesh[C]//Proceedings of Geometric Modeling and Processing.Heidelberg:Springer Verlag,2008:33-46. |
| Cited By in Cnki (93) | |
| [14] | 陈甜甜,赵罡. 半规则三角网格模型细分曲面重构[J].北京航空航天大学学报,2012,38(9):1245-1249. Chen T T,Zhao G.Semi-regular triangular mesh subdivision surface reconstruction[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(9):1245-1249(in Chinese). |
| Cited By in Cnki (198) | |
| [15] | 李桂清,吴壮志, 马维银.自适应细分技术研究进展[J].计算机辅助设计与图形学学报,2006,18(12):1789-1798. Li G Q,Wu Z Z,Ma W Y.Research advances in adaptive subdivision techniques[J].Journal of Computer-Aided Design & Computer Graphics,2006,18(12):1789-1798(in Chinese). |
| Cited By in Cnki (309) | |
| [16] | Flutter A, Todd J.A machining strategy for tool making[J].Computer-Aided Design,2001,33(13):1009-1022. |
| Click to display the text | |
| [17] | Jun C S, Kim D S,Park S.A new curve-based approach to polyhedral machining[J].Computer-Aided Design,2002,349(5): 379-389. |
| Click to display the text | |
| [18] | Bentley J L, Ottmann T A.Algorithm for reporting and counting geometric intersections[J].IEEE Transactions on Computers,1979,C-28(9):643-647. |
| Click to display the text |
