1 修正M-K模型建立1.1 传统M-K假设传统M-K模型以凹槽假设为理论核心,认为板材具有不可避免的厚度不均性,这种不均性用凹槽表示,如图 1所示.根据假设,板材的集中性失稳是由板材表面初始存在的缺陷引起的.该模型广泛用于预测平面应力条件下的板材成形极限,理论假设包括以下几点[5].
 |
| 图 1 M-K模型理论框架图Fig. 1 Theoretical frame diagram of M-K model |
| 图选项 |
1) 简单加载条件:A区主应力及主应变均成比例增加且在整个变形过程中比值为常数;2) 变形协调条件:B区第二主应变增量dε2b与A区第二主应变增量dε2a相等,即dε2a=dε2b=dε2;3) 力平衡条件:A区与B区第一主方向力始终平衡,即F1a=F1b.为考虑板材的厚向异性,在模型推导中采用Hill′48塑性屈服准则[16]:
式中,ξ为厚向异性指数;σ1,σ2,σ3分别为1,2,3主应力分量.A区—变形安全区;B区—不均匀变形区;
ta,tb—变形过程中A,B区板材的厚度
1.2 韧性断裂准则根据应变能理论,材料的塑性变形程度可以用总塑性功来体现,其表达式[17]为
式中,σ为等效应力;ε为等效应变;U为总塑性功.在采用积分函数的基础上,该判据具有考虑非线性应变路径变化的优点.Cockcroft和Latham(C-L)等[17]考虑最大拉伸主应力在材料变形至断裂过程中的作用,提出如下公式:
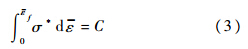
式中,σ*为最大拉伸主应力.这个准则应用最为广泛,在本文中,将以此(C-L准则)为基础与传统M-K模型假设结合,进行板材成形极限曲线的预测.同时,为保证积分值始终为正值,对C-L准则的左半部分取绝对值.
1.3 推导过程假设图 1中平面内应力主轴方向的主应力比值为α=σ2/σ1(0≤α≤1),G1=2ξ/(1+ξ),在平面应力状态下,则式(1)可表示为
等效应力与最大主应力方向的比值为
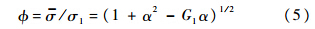
由Levy-Mises增量理论关系式,有
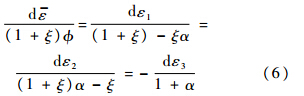
记ρ为面内应变比值,β为等效应变与第一主应变比值.分别表示如下:
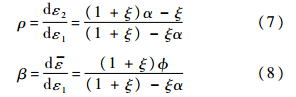
根据力平衡条件的理论假设,可得:
板材厚度法向方向的应变,即
可表示为
式中,t为变形过程中的板材厚度;t0为初始的板材厚度.已知f0=tb0/ta0,可得变形过程中板材厚度不均度为
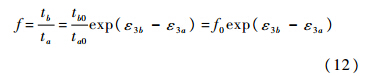
结合式(1)、式(9)、式(12),得到以下平衡方程:
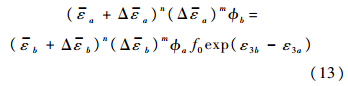
对式(13)采用Newton迭代法进行计算,分析板材集中性失稳行为,得到板材变形过程中A区和B区的各应力应变值.此时,引入韧性断裂准则的通式:
对B区进行判断,当
时,得到对应时刻的A区面内主应变ε1a,ε2a,作为相应α=σ2/σ1值下的成形极限点.对α=σ2/σ1在0≤α≤1范围内进行遍历,得到板材的成形极限曲线.2 韧性断裂准则中材料常数的确定本文所用材料为1 mm厚的AA7075-O铝合金板材,对其进行单向拉伸试验以确定应力应变曲线,试件的几何尺寸如图 2所示.试验在北京航空航天大学的WDW-100电子万能试验机上进行(如图 3所示).
 |
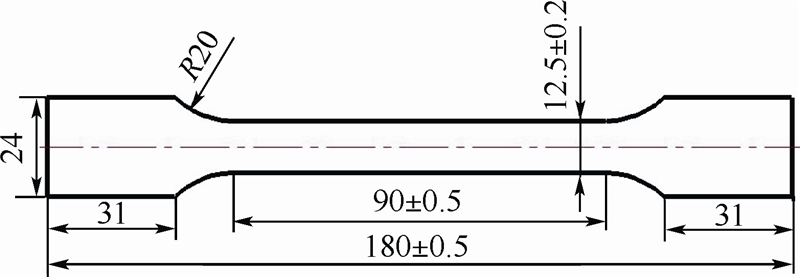| 图 2 AA7075-O铝合金单拉试样的几何形状及尺寸Fig. 2 Uniaxial tensile specimen geometry and dimension of AA7075-O aluminum alloy sheet |
| 图选项 |
 |
| 图 3 单向拉伸试验设备Fig. 3 Uniaxial tensile experimental equipment |
| 图选项 |
针对单拉试验数据,考虑各参数对AA7075-O铝合金板材力学性能的影响,对Swift模型进行修正,得到本构方程:
本构方程中的材料参数K,n,m,q,p通过拟合确定,同时计算得到板材厚向异性指数和弹性模量E,如表 1所示.在拉伸速率v=15 mm/min情况下,拟合得到应力应变曲线与试验结果对比如图 4所示,结果符合较好.
表 1 材料性能参数Table 1 Material performance parameters
| 参数 | E/GPa | n | m | K/MPa | ξ | q | p |
| 数值 | 71 | 0.458 | 0.023 | 804 | 0.713 | 35.48 | 2.19 |
表选项
 |
| 图 4 拟合应力应变曲线与试验数据比较Fig. 4 Comparison of stress-strain curve between fitting and experimental data |
| 图选项 |
为确定韧性断裂准则中的材料常数,本文采用单向拉伸数值模拟和试验对比的方法.利用Abaqus/Explicit进行有限元分析,材料参数采用表 1中的数据.数值模拟得到试件的载荷-位移曲线,与试验得到的曲线对比结果如图 5所示,二者符合较好,该条件下的模拟参数可信.图 6为试件拉断时等效应变分布云图,将危险单元在变形过程中的应力应变历史代入C-L准则
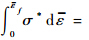C, 可以得到材料常数C=192.43. |
| 图 5 有限元计算与试验得到的载荷-位移曲线对比Fig. 5 Comparison of loading-displacement curve between FEM and experimental data |
| 图选项 |
 |
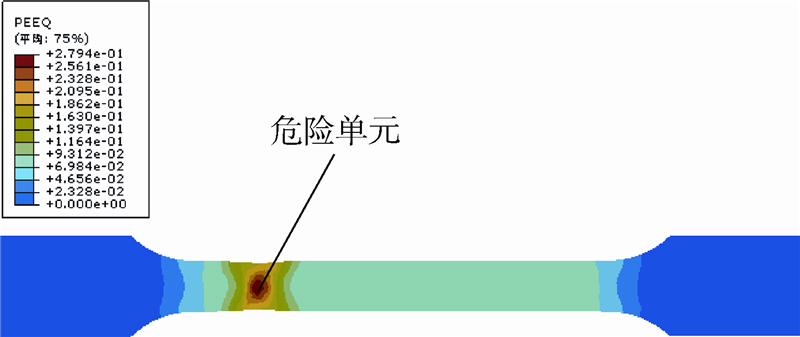| 图 6 临近拉断时刻等效塑性应变分布云图Fig. 6 Equivalent plastic strain distribution close to failure |
| 图选项 |
3 成形极限理论预测与试验验证在修正M-K模型中,为确定初始厚度不均度值,利用MATLAB编程获得.流程如下:1) 设定f0初值,遍历α=σ2/σ1(0≤α≤1),得到板材的理论成形极限曲线;2) 比较单向拉伸试验所得成形极限点与理论成形极限曲线差值,差值为正,则增大f0值;差值为负,减小f0值;直至差值小于0.005为止;利用该方法确定f0=0.955,并得到理论成形极限曲线.同时,利用单向拉伸、宽板弯曲、液压胀形试验得到AA7075-O铝合金板材在常温下的成形极限,试验件如图 7所示.
 |
| 图 7 单向拉伸、宽板弯曲、胀形试验件Fig. 7 Test pieces for uniaxial tensile,wide plate bending and hydrobulging |
| 图选项 |
图 8为利用修正的M-K模型及传统M-K模型分别得到的理论成形极限曲线与成形极限试验点的对比图.由图可知,与传统M-K模型相比,修正的M-K模型能更好地预测AA7075-O铝合金板材的成形极限曲线,与成形极限试验点贴合度更高.
 |
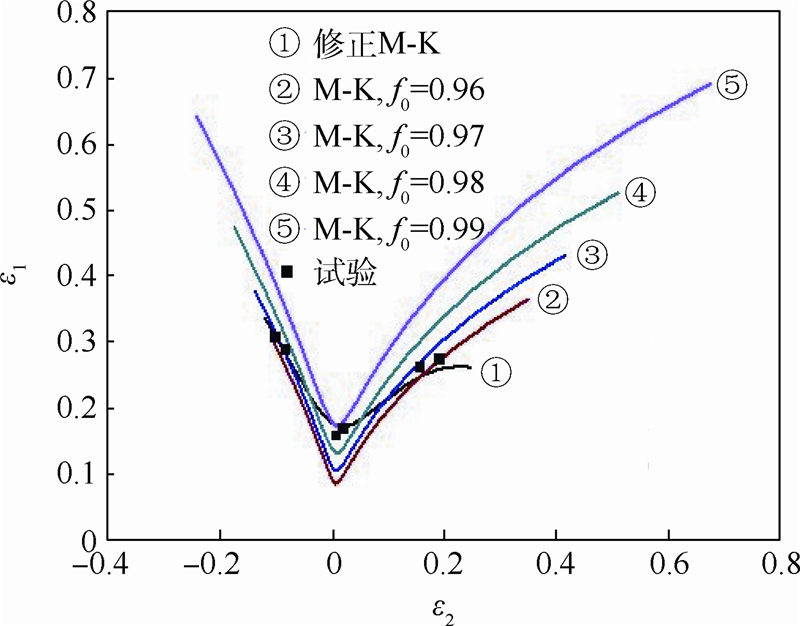| 图 8 成形极限对比图Fig. 8 Comparison of forming limit |
| 图选项 |
4 对比分析在传统M-K模型中,板材破裂失效时的判断准则为B区第一主应变增量Δε1b与A区第一主应变增量Δε1a的比值是常数,即,Δε1b/Δε1a=10.该判断准则表明Δε1b/Δε1a值与加载路径无关.同时,由修正M-K模型所得到的Δε1b/Δε1a值如图 9所示.从中可以看出,随着α从0到1遍历,Δε1b/Δε1a值先增大后减小.在α=0.5附近,该值达到极值.Δε1b/Δε1a值的变化趋势同样可以在成形极限图中得到反映.如图 8所示,f0=0.96时的传统M-K模型预测的成形极限曲线,在单向拉伸和双向拉伸点处与试验点接近;在平面应变处,远低于试验值.由此可知,只有通过提高平面应变加载路径下的Δε1b/Δε1a值作为判断准则,才能提高该处的成形极限值.修正M-K模型中Δε1b/Δε1a值的变化趋势与实际相符,表明以C-L韧性断裂准则能更加准确地反应A区凹槽的破坏,用于预测板材的成形极限曲线.
 |
| 图 9 α从0到1遍历下Δε1b/Δε1a值分布图Fig. 9 Distribution of Δε1b/Δε1a when α ranges from 0 to 1 |
| 图选项 |
5 结 论本文将传统M-K模型框架和基于应变能的韧性断裂准则相结合,提出一种修正的M-K模型预测板材的成形极限曲线,并进行了数值计算和试验对比验证.1) 利用单向拉伸数值模拟和试验相结合的方法,得到C-L韧性断裂准则中的材料常数.基于单向拉伸试验所得成形极限点,通过MATLAB编程得到修正M-K模型的初始厚度不均度.结果表明,针对同种规格板材及试验条件,材料常数及初始厚度不均度为定值.2) 试验得到AA7075-O铝合金板材的成形极限,对比表明,M-K模型中A区凹槽破裂失效时的判断准则应修正为C-L韧性断裂准则,与试验符合程度更高,验证了本文提出的修正M-K模型的正确性.
参考文献
| [1] | Swift H W. Plastic instability under plane stress[J].Journal of the Mechanics and Physics of Solid,1952,1(1):1-18. |
| Click to display the text | |
| [2] | Hill R. On discontinuous plastic states with special reference to localized necking in thin sheets[J].Journal of Mechanics and Physics of Solids,1952,1(1):19-31. |
| Click to display the text | |
| [3] | Stören S, Rice J.Localized necking in thin sheets[J].Journal of the Mechanics and Physics of Solid,1975,23(6):421-441. |
| Click to display the text | |
| [4] | Zhu X H, Weinmann K,Chandra A.A unified bifurcation analysis of sheet metal forming limits[J].Journal of Engineering Materials and Technology,2001,123(3):329-333. |
| Click to display the text | |
| [5] | Marciniak Z, Kuczynski K.Limit strains in the processes of stretch-forming sheet metal[J].International Journal of Mechanical Science,1967,9(3):609-620. |
| Click to display the text | |
| [6] | 杜平梅,郎利辉, 刘宝胜,等.基于M-K模型的成形极限预测及参数影响[J].塑性工程学报,2011,18(5):84-89. Du P M,Lang L H,Liu B S,et al.Theoretical prediction and parameter influence of FLDs based on M-K model[J].Journal of Plasticity Engineering,2011,18(5):84-89(in Chinese). |
| Cited By in Cnki (354) | |
| [7] | 马高山,万敏, 吴向东.基于M-K模型的铝锂合金热态下成形极限预测[J].中国有色金属学报,2008,18(6):980-984. Ma G S,Wan M,Wu X D.Theoretical prediction of FLDs for Al-Li alloy at elevated temperature based on M-K model[J].The Chinese Journal of Nonferrous Metals,2008,18(6):980-984(in Chinese). |
| Cited By in Cnki (288) | |
| [8] | Assempour A, Nejadkhaki H K,Hashemi R.Forming limit diagrams with the existence of through-thickness normal stress[J].Computational Materials Science,2010,48(3):504-508. |
| Click to display the text | |
| [9] | 陈劼实,周贤宾. 成形极限预测韧性断裂准则及屈服准则的影响[J].北京航空航天大学学报,2006,32(8):969-973. Chen J S,Zhou X B.Suitability of some ductile fracture criteria and yield criteria in forming limit prediction[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(8):969-973(in Chinese). |
| Cited By in Cnki (608) | |
| [10] | 谢延敏,于沪平, 陈军,等.板料成形中韧性断裂准则应用研究进展[J].工程设计学报,2007,14(1):6-10. Xie Y M,Yu H P,Chen J,et al.Recent advances of research on application of ductile fracture criteria in sheet metal forming process[J].Journal of Engineering Design,2007,14(1):6-10(in Chinese). |
| Cited By in Cnki (594) | |
| [11] | Takuda H, Mori K.Finite element analysis of limit strains in biaxial stretching of sheet metals allowing for ductile fracture[J].International Journal of Machine Tools and Manufacturing,2000,42(4):785-798. |
| Click to display the text | |
| [12] | Lei L P, Kim J.Bursting failure prediction in tube hydroforming process by using rigid-plastic FEM combined with ductile fracture criterion[J].International Journal of Mechanical Sciences,2002,44(7):1411-1428. |
| Click to display the text | |
| [13] | 高付海,桂良进, 范子杰.基于韧性准则的金属板料冲压成形断裂模拟[J].工程力学,2010,27(2):204-208. Gao F H,Gui L J,Fan Z J.Numerical simulation of the fracture in sheet metal stamping based on ductile criterion[J].Engineering Mechanics,2010,27(2):204-208(in Chinese). |
| Cited By in Cnki (395) | |
| [14] | Vallellano C, Morales D,Garcia-Lomas F J.A study to predict failure in biaxially stretched sheets of aluminum alloy 2024-T3[J].Materials and Manufacturing Processes,2008,23(3):303-310. |
| Click to display the text | |
| [15] | Jain M,Allin J, Lloyd D J.Fracture limit prediction using ductile fracture criteria for forming of an automotive aluminum sheet[J].International Journal of Mechanical Sciences,1999,41(10) :273-288. |
| Click to display the text | |
| [16] | Hill R. A theory of the yielding and plastic flow of anisotropic metals[C]//Proceedings of the Royal Society of London Series A.London:The Royal Society,1948:281-297. |
| Click to display the text | |
| [17] | Takuda H, Mori K,Hatta N.The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals[J].Journal of Materials Processing Technology,1999,95(1-3):116-121. |
| Click to display the text |
