矩的显式积分算法研究与应用

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-25

在采用有限元方法^[1]进行刚度矩阵计算、求解物体体积、求解物体的惯性矩^{[2, 3, 4]}等各种力学参数时,常常需要涉及矩的计算.Soerjadi等^[5]给出了在二维平面情况下的计算公式.该公式基于格林公式的一个特例得到,令格林公式中,向量场函数的任意一项恒为0,导出将面积分转化为线积分的通式,然后将线积分用空间已知点的值表示出来,继而得出面积分的值.然而,该方法要求向量场函数面积分项中只有一项,且该项需含有对空间所有维度的微分项,因此在三维或更高维度的空间中,无法继续用该方法得到结果.Johnson和Mirtich等^{[1, 6]}提出了在三维空间进行体积矩积分的方法.该方法首先对于给定的标量场函数构造了一个向量场函数的散度形式,然后通过高斯公式将该向量场函数的散度转化为向量场在计算域表面的积分,随后将该积分拆写成标量场积分的形式,实现了将三维的体积矩转化为二维的面矩,随后再通过斯托克斯公式将面矩的积分转化为线积分和低阶面矩的和的形式,通过递归,得出计算域的矩.虽然该方法解决了三维空间中体积矩的计算问题,但是仍存在几点不足.首先,在通过斯托克斯公式将面矩转化为线积分与低阶面矩和的形式的时候,推导非常复杂;其次,过多地使用了递归计算,在程序实现上会增大运行时的开销;最后该方法只适用于三维空间中的体积矩,对于高维空间中的矩无法计算得到.Sheynin等^{[7, 8, 9]}给出了求解计算域任意阶矩的公式.并将其推广到了高维空间,该方法未使用降维或递归的手段,而是直接给出了矩的显式表达式,降低了问题的复杂度.然而该表达式不便于计算机实现.本文在Sheynin等基础之上推导了n维空间中的便于计算机程序实现的矩的显示公式.并基于在三维空间的公式,使用Python与Fortran混编的技术,实现了三维空间下矩的计算,并以Boeing777-200LR为例,给出了一个算例,评估了并行计算的效能,并和逐次降维法进行了对比.1 矩的定义与公式推导1.1 矩的定义及物理意义首先给出矩的定义,如式(1)所示,以下就该公式的计算进行讨论.

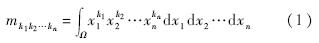
式中,x₁,x₂,…,x_n为n维空间中的坐标;m_{k₁k₂…k_n}为在x₁,x₂,…,x_n上的k₁,k₂,…,k_n阶矩;Ω为积分计算域.当k₁=k₂=…=k_n=0时,m_{k₁k₂…k_n}具有体积的物理意义,公式如下:

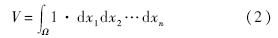
而当

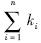=2时,m_{k₁k₂…k_n}具有惯性矩的物理意义,简单起见,考虑三维空间中刚体的惯性矩张量I,有

式中，对角线上的I_xx,I_yy,I_zz分别为在x,y,z轴上的转动惯量,其定义如下所示:

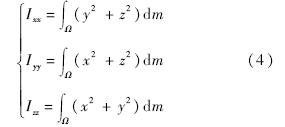
而非对角元素则是惯量积,定义如下所示:

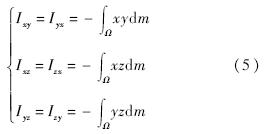
由上可见,体积和惯性矩都可以通过矩积分的方式来获取.下面先给出三维空间中矩的公式以及推导过程,随后将其推广到n维空间中.1.2 计算域的分割对于不规则计算域的通式推导是困难的.因此本文首先将任意形状的计算域进行分割,将整个计算域(Ω)转化为若干个三角形包围的多面体,再在这若干个四面体中进行计算,最后将结果叠加.在进行四面体矩的计算时,通过坐标变换的方法在顶点为原点、3条棱与坐标轴重合且长度为1的四面体(称作标准四面体)上进行计算,从而得到任意四面体的矩.对于空间中的任意计算域,首先将其几何外形用三角形面片进行近似离散,对于每一个三角形,将其3个顶点与原点相连,便能够得到若干以三角形为底,以原点为顶点的四面体,如图 1所示.本文定义四面体和原点相接的3条棱的另一个端点的次序和三角形表面法向量满足右手定则,然后分别在每一个四面体上进行积分,得到每一个四面体的矩,然后将这些四面体的矩相加,由于有方向的定义,所有集合体外部的矩都会被抵消,因此所有四面体矩的和即是计算域的矩.令T表示用三角化离散后的计算域,在T中,有r个顶点在原点的四面体,记作T_i,有

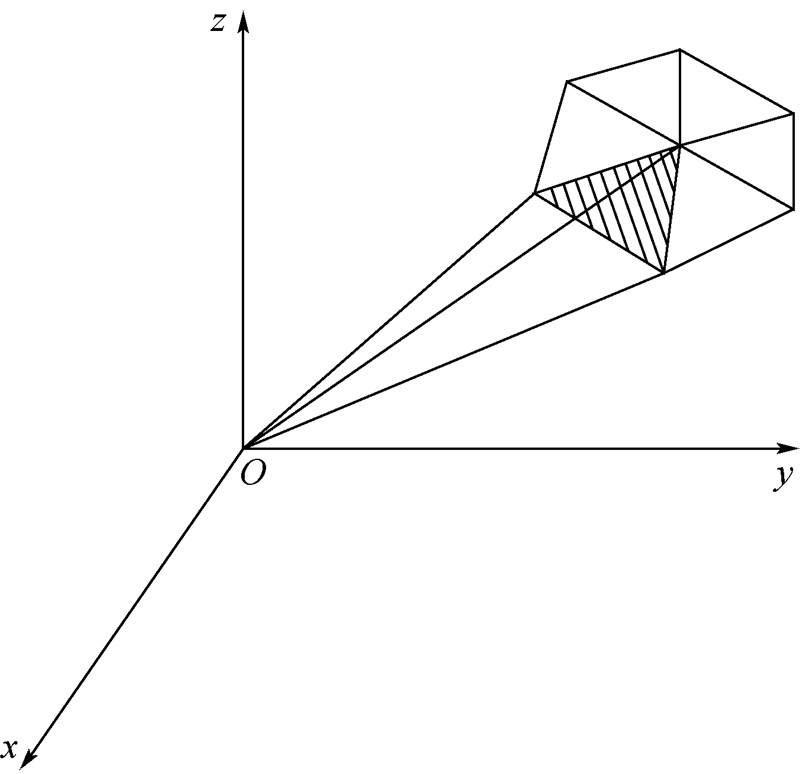图 1 空间四面体的定义Fig. 1 Definition of tetrahedron

图选项

1.3 n维空间下标准四面体公式首先推导在n维空间下的标准四面体的计算公式.n维空间标准四面体积分定义为

式中,x₁,x₂，…，x_n≥0,x₁+x₂…+x_n≤1.使用Dirichlet积分公式有

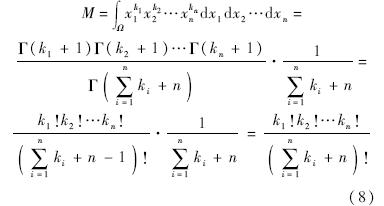
式中,Γ(n)表示伽马函数,定义为Γ(n)=(n-1)!.1.4 三维空间任意四面体的矩对于三维空间中任意四面体的矩,可以采用直接积分的方法来得到.首先,选取四面体与原点相接的3条棱为新的坐标系,将四面体用它的3条边表示,记作T(a,b,c),其中a,b,c都是列向量,且a=(a₁,a₂,a₃)^T,b=(b₁,b₂,b₃)^T,c=(c₁,c₂,c₃)^T,从而得到从旧坐标到新坐标的变换矩阵(a,b,c)^－1,记作A,其中的元素为{a_ij},在旧坐标系下变量用x_i表示,而新坐标系下的变量用y_i表示,则坐标转换关系为x=Ay.记体积矩为m_k₁k₂k₃(T),i,j,k为直角坐标系的基,将向量x用Ay替换,即

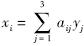,有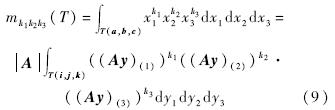

式中，(Ay)_(i)代表向量Ay的第i个分量.

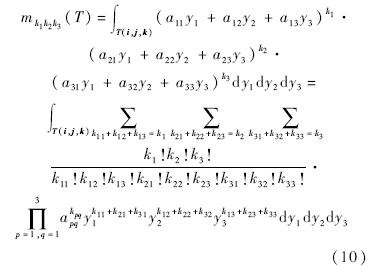
这里,使用到了多项式展开定理.式中,

表示对所有满足k_i1+k_i2+k_i3=k_i的组合进行求和^[10].再代入标准四面体矩公式得：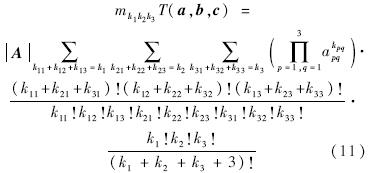

1.5 矩公式在高维空间的推广将三维空间的通式向高维空间推广,容易得到高维空间中的矩公式:

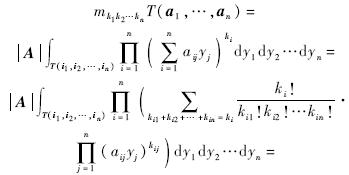
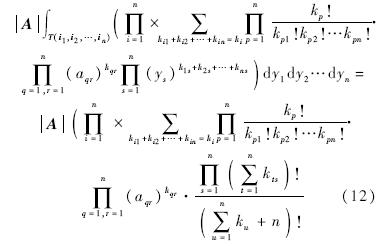
式中，

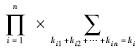表示n个求和号累加的形式.由于多重求和号可以通过多重循环实现,因此该形式易于计算机程序设计.2 矩的并行计算算法在第1节中,推导了三维空间下任意矩积分的公式.在本节,基于该公式设计出矩的并行计算算法,并对并行、串行显式积分公式算法和Mirtich^[6]提出的逐次降维法进行比较.2.1 矩的并行显式积分公式算法由计算域的分解可知,矩的计算需要求出n个四面体的矩,然后将其相加,而这部分计算是相互间没有关联的,因此,可以通过并行计算的方法来实现,实现原理如图 2所示.

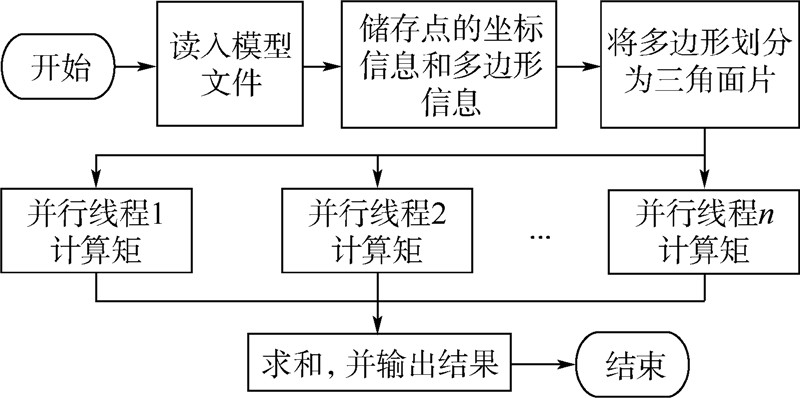图 2 并行算法流程图Fig. 2 Flowchart of parallel algorithm

图选项

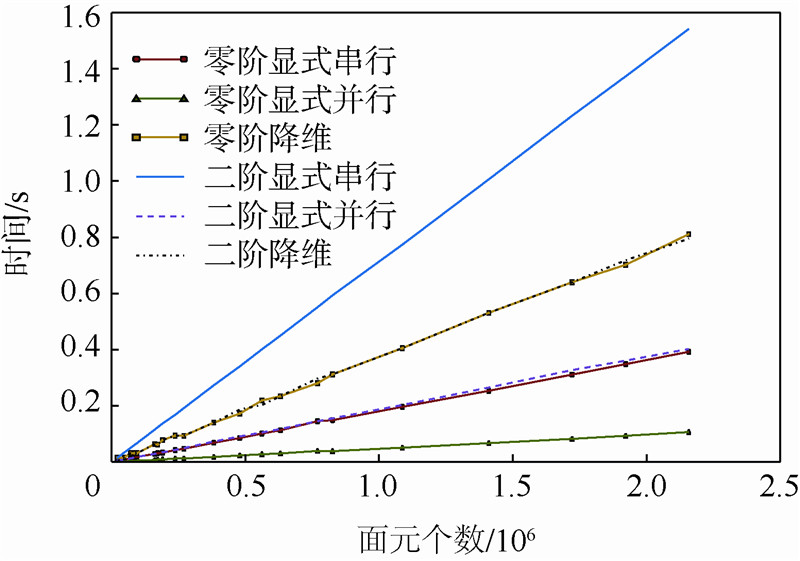
本次计算采用Boeing777-200LR的三角化表面网格(图 3)作为测试几何体.通过设置不同的三角剖分精度,得到了不同层级的网格.通过对单位密度几何体的零阶矩∫_Ω1dm和二阶矩∫_Ωy²dm的计算,比较了3种方法的效率.

图 3 几何体表面三角网格Fig. 3 Surface triangular mesh of geometry

图选项

为了简化几何处理的复杂度,该程序使用Python^{[11, 12]}做外部接口;为了提升计算速度,实现并行计算,采用Fortran做底层计算,并行的部分也由Fortran来实现.并行的部分通过在Fortran代码中加入OpenMP^{[13, 14]},将循环自动地分配到各个CPU上,提高计算效率.计算环境使用IntelCore^TM i7-3770 CPU主频3.4 GHz 4核8线程8 GB RAM.2.2 结果分析通过对不同精度的Boeing777-200LR网格^[15]进行计算,结果如图 4和表 1所示.

图 4 算例结果分析Fig. 4 Example results analysis

图选项

表 1 计算结果 Table 1 Calculation results

单元数	零阶矩					二阶矩
	显式积分公式法			逐次降维法		显式积分公式法			逐次降维法
	矩/kg	串行时间/ms	并行时间/ms	矩/kg	时间/ms	矩/(kg·m²)	串行时间/ms	并行时间/ms	矩/(kg·m²)	时间/ms
205 24	66 373	3	2	66 373	16	2 004 112	16	0	2 004 112	0
269 948	66 689	47	12	66 689	93	2 024 921	109	47	2 024 926	94
478 990	66 700	85	23	66 700	172	2 025 507	218	63	2 025 511	187
631 228	66 704	113	30	66 704	234	2 025 687	281	93	2 025 692	234
769 506	66 705	145	39	66 705	280	2 025 790	343	109	2 025 795	297
1 087 336	66 708	196	51	66 708	405	2 025 976	499	156	2 025 982	405
1 721 682	66 710	311	82	66 710	640	2 026 108	764	234	2 026 113	640
2 158 232	66 711	392	106	66 711	811	2 026 154	967	250	2 026 159	795

表选项

在该算例中,分别通过串行和并行的显式积分公式算法,计算了几何体的零阶和二阶矩,并和逐次降维法做了对比.可以看出,随网格数的增大,计算时间线性增加;在同等情况下,并行效率大致为串行效率的3.7倍;在计算零阶矩时,显式积分公式法效率高于逐次降维法,而当矩的阶数增大时,逐次降维法的效率较高,但仍低于并行的显式积分公式法;显式积分公式法能很快推广到高维空间,而逐次降维法仅限于三维空间中.在程序并行计算时,由于CPU 4核8线程一个核上的两线程存在干扰,不便于比较效率,因此在这里关闭CPU的超线程功能进行测试,相当于4核并行,效率达到了3.7倍左右,由于OpenMP运行的资源消耗,不能达到理想中4倍的运行效率.对比矩的计算结果误差可知,矩的积分误差主要发生在几何体的离散过程中.随着网格数增加,矩的值同时增大,而最后趋于收敛,对比第1组计算结果和最后一组计算结果,有4.5%的误差,这是由于离散网格随网格数的增加而逐渐贴近于真实边界.其次,对比显式积分公式算法和逐次降维法在相同离散网格下的结果可知,由离散求和造成的矩计算的误差小,其数量级约在10^-6左右.其原因是离散几何体矩的计算直接用公式表出,因此其计算误差只表现有限数值精度导致的舍入误差上.综上,矩积分计算的误差主要由几何体离散导致,在实际计算时,需要采用合适的离散网格数进行离散.3 结论通过分析和计算表明:1) 将计算域用三角面片离散的方式,能有效地将任意计算域转为多面体,简化了计算;2) 显式积分公式利于在计算机上实现,能方便地推广到高维空间,逐次降维法无法推广;3) 随着面元数量的增加,并行和串行计算消耗时间都随之线性增长,在测试计算机上并行计算的效率约为串行效率的3.7倍;4) 矩的计算结果随着网格的细化而逐渐趋于收敛.

参考文献

[1]	Johnson F T, Samant S S,Bieterman M B,et al.TRANAIR-a computer code for transonic analyses of arbitrary configurations,NASA-CR-4348[R].Washington,D.C.:NASA,1987.
	Click to display the text
[2]	洪国雄. 惯性张量的物理意义[J].大学物理,1989,12(1):7-8. Hong G X.The physical meaning of the inertia tensor[J].College Physics,1989,12(1):7-8(in Chinese).
	Cited By in Cnki (1)
[3]	秦莉,杨明, 郭庆.遗传算法在质量矩导弹姿态控制中的应用[J].北京航空航天大学学报,2007,33(7):769-772. Qin L,Yang M,Guo Q.Movingmass attitude control law based on genetic algerithm[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(7):769-772(in Chinese).
	Cited By in Cnki (10)
[4]	徐水源. 惯性矩与惯性张量的关系[J].黄石教育学院学报,2005,22(4):90-92. Xu S Y.The relationship of the moment of inertia and inertia tensor[J].Journal of Huangshi Education College,2005,22(4):90-92(in Chinese).
	Cited By in Cnki (5)
[5]	Soerjadi R. On the computation of the moments of a polygon,with some applications[M].Netherlands:Stevin Laboratory,1968:43-58.

[6]	Mirtich B. Fast and accurate computation of polyhedral mass properties[J].Journal of Graphics Tools,1996,1(2):31-50.
	Click to display the text
[7]	Sheynin S, Tuzikov A,Vasiliev P.Efficient computations of body moments[J].Информационные Процессы,2002,2(1):22- 23.

[8]	Sheynin S A, Tuzikov A V.Explicit formulae for polyhedra moments[J].Pattern Recognition Letters,2001,22(10):1103- 1109.
	Click to display the text
[9]	Tuzikov A V, Sheynin S A,Vasiliev P V.Computation of volume and surface body moments[J].Pattern Recognition,2003,36(11): 2521-2529.
	Click to display the text
[10]	Hall M. Combinatorial theory[M].New York:John Wiley & Sons,1998:166.

[11]	VanRossum G, Drake F L.Python language reference manual[M].United Kingdom:Network Theory,2003.

[12]	VanRossum G, Drake F L.The python language reference[M].Beaverton,OR,USA:Python Software Foundation,2010.

[13]	Chandra R. Parallel programming in OpenMP[M].San Francisco:Morgan Kaufmann,2001.

[14]	Dagum L, Menon R.OpenMP:an industry standard API for shared-memory programming[J].Computational Science & Engineering,IEEE,1998,5(1):46-55.
	Click to display the text
[15]	Fredericks W J, Antcliff K R,Costa G,et al.Aircraft conceptual design using vehicle sketch pad[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston:American Institute of Aeronautics and Astronautics Inc,2010:1-17.
	Click to display the text