半实物仿真技术是系统仿真技术的一个重要分支,它可以通过构建目标/环境模拟器逼真地生成真实条件下的目标/环境场景进行仿真试验,而且还可以将系统中某些非线性较高的关键部件实物引入仿真回路,从而可以提高仿真的可信度[7].据美国大西洋导弹测试基地的统计,“美国军方90%的武器系统的鉴定、评估数据来自于半实物仿真的结果”,我国的航天、航空部门也规定“未经过半实物仿真的产品不能参与发射或飞行测试”[8].未来能否将地磁匹配导航技术成功应用于工程实际,半实物仿真试验评估是其中的一个关键性的制约因素.本文利用现有条件搭建了地磁匹配导航半实物仿真系统,通过引入磁场仿真环境和磁传感器,从测量噪声、匹配长度、匹配区域和惯导误差这4个影响算法性能的因素出发,对等值线(ICCP)匹配算法进行评估,使仿真条件更加接近真实情况,结论更加可信.
1 地磁导航匹配算法1.1 ICCP算法原理 地磁导航最终的目的是要实现导航定位,因此地磁导航匹配算法是地磁匹配导航的核心技术,算法的优劣对导航定位的精度及其可靠性具有举足轻重的作用.目前研究较多的是ICCP算法[9, 10].
ICCP算法基于几何学原理,它的实质是匹配多边弧.它的匹配过程基于寻找最近等值线点,用最小方差估计的方法,通过计算测量点与真实位置点之间的刚性变换(包括旋转和平移),经过多次迭代,使得两弧之间的量测距离不断减小,从而得到最优估计航迹,其原理图如图 1所示.
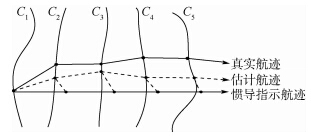 |
| 图 1 等值线(ICCP)算法原理示意图Fig. 1 Principle of iterated closest contour point (ICCP) algorithm |
| 图选项 |
地磁匹配ICCP算法的具体步骤如下.
步骤1 从地磁基准图中提取与测量磁场值对应的等值线集C.
步骤2 以各测量点为初始迭代值,令 G k=[g 1,g 2,…,g n],对于每个测量点,在相应的等值线上寻找与其最近的点 y i.令 Y k=[y 1,y 2,…,y n],寻找刚性变换 T k,使相关极值函数dk 最小:
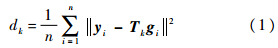
步骤3 对矩阵 G k应用变换 T k,即 G k+1= T k G k.
步骤4 判断终止条件,如果系统满足最终的收敛条件dk-1-dk≤τ(τ为设定的阈值)或迭代次数K>Kmax,则计算结束,否则返回步骤2继续迭代.
于是可以归纳得到ICCP算法的流程如图 2所示.
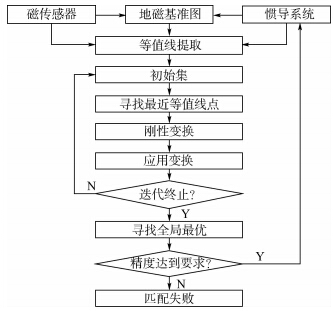 |
| 图 2 等值线(ICCP)算法流程图Fig. 2 Flow chart of iterated closest contour point (ICCP) algorithm |
| 图选项 |
从图 2中可以看出,ICCP算法是采取“寻找最近等值线点—计算刚性变换—应用变换”的循环过程.
1.2 影响ICCP算法性能的因素分析虽然匹配算法原理的研究和匹配算法的改进是算法研究的重点,但是影响算法性能的因素是直接影响算法可行性的关键[11, 12].因此有必要对影响算法性能的因素进行理论上的分析.
1.2.1 测量噪声从算法的具体步骤可以知道,测量得到的磁场值作为寻找等值线的基准值,对算法起着至关重要的作用.而在地磁匹配导航实时图测量过程中,由于受多种因素的影响,磁传感器测得的磁场值必然加入了外界噪声,这使得提取出来的等值线存在误差,即算法的步骤1存在误差,而从步骤2~步骤4循环过程是基于步骤1进行的,故由此可以推测:如果测量噪声太大,即使算法经过多次循环迭代收敛,也只能收敛于错误的结果,导致匹配失败.
1.2.2 匹配长度在地磁匹配过程中,匹配长度越大,实时图中所包含的信息量就越大,理论上匹配成功的概率也就越大.但是匹配长度增大时,测量周期会延长,从而在有限的匹配区域内的匹配次数会减少,不能最大限度地对惯导的误差进行修正.同时,由于匹配长度的增加,算法的计算量会随之增加,实时性必然会降低.因此需要寻找合适的匹配长度.
1.2.3 匹配区域匹配算法对地磁场特征的依赖性较强,需要具有满足匹配要求的地磁匹配区域.地磁匹配区域内的地磁场特征参数相关程度如果太高,磁传感器测得的实时图中就不能包含区别于其他位置的信息量,就可能会对正确匹配造成干扰.因此匹配区域的选择对算法的影响也很大.
1.2.4 惯导误差由于惯导长时间工作时会产生漂移,故惯导误差对算法的影响不能忽略.如果惯导误差较小,那么经过有限次刚性变换后的点集能够以极大的概率落在能收敛到全局最优的区域内,从而得到全局最优解.相反,如果惯导误差太大,即使经过多次变换,也只能收敛到局部极小值而非全局极小值,导致匹配失败.
2 地磁匹配导航半实物仿真系统构建地磁匹配导航原理是:把预先规划好的航迹上某些点的地磁场特征量绘制成地磁基准图,存储在载体导航计算机中,当飞行器飞越匹配区时,由地磁场测量仪器实时测量出飞越点的地磁场特征量,并构成实时测量序列,与导航计算机中的地磁基准图进行匹配,即通过一定的地磁匹配算法估算出飞行器的坐标位置,从而修正惯导误差,以达到精确导航的目的[13].依据地磁匹配导航原理,本文利用现有条件搭建了地磁匹配导航半实物仿真系统,其结构组成如图 3所示.
 |
| 图 3 地磁匹配导航半实物仿真系统Fig. 3 Hardware-in-the-loop simulation system of geomagnetic matching navigation |
| 图选项 |
地磁匹配导航半实物仿真系统由小型磁屏蔽筒、螺线管线圈、磁力仪探头、磁力计、仿真计算机和高稳定度程控电流源组成一个闭环的仿真回路,目的是将实验室环境下难以实现的载体相对于磁场的运动转变为磁场相对于载体的运动.
由文献[14, 15]知,地磁匹配的最优特征量选择地磁场总强度为宜,因此系统对地磁场总强度环境进行模拟仿真.地磁场环境仿真由小型磁屏蔽筒、螺线管线圈、高稳定度程控电流源和仿真计算机组合实现.其中小型磁屏蔽筒为半实物仿真提供一个干净的、不受外界磁场干扰的零磁空间;高稳定度程控电流源通过控制线圈中电流的大小和方向,从而在螺线管线圈内部产生一个均匀的单一方向的磁场,模拟地磁场总强度的大小;仿真计算机通过在地磁场基准图中读取预选路径上的磁场值,转换为螺线管线圈产生相应磁场的电流值,通过RS232串口以一定的频率发送至高稳定度程控电流源,控制电流源的电流输出,从而使螺线管线圈产生需要的磁场值来模拟载体飞行路径上的磁场环境.经中国计量科学研究院计量,该地磁总场仿真环境可以生成0~100 000 nT的磁场值,其不确定度为:20 000 nT以下,U=1 nT(k=3);20 000~100 000 nT,U=0.5 nT(k=3).可见系统模拟的磁场精度极高,能够真实准确地模拟飞行航迹上的磁场环境.
地磁场实时测量由放置于螺线管线圈内部的磁力仪探头和磁力计组合实现.其中磁力仪探头敏感其所在位置的磁场变化,将磁场测量数据由磁力计以一定的频率发送至仿真计算机中.由于螺线管线圈中电感的存在,在电流源的输出改变瞬间,线圈中的电流不能突变,因而也不能立刻生成需要的稳定磁场.经测试,当电流改变时,磁场稳定最长需要1 s的时间,而本系统中磁力仪探头的采样频率为10 Hz,因此,当电流改变后磁力仪探头测得的前10个数据不能用于半实物仿真,这就要求电流改变的时间间隔必须大于1 s才能保证磁力仪探头采集到需要的磁场值.
地磁匹配解算由磁力仪探头测得的磁场值与地磁基准图通过地磁匹配ICCP算法解算模块进行定位解算,从而输出位置信息.
3 仿真试验针对影响ICCP算法性能的各因素,基于建立的地磁匹配导航半实物仿真系统,进行动态仿真试验.本文定义定位误差在一个网格以内为匹配成功.为了避免一次匹配存在偶然性,相同试验条件下进行20次匹配试验,通过匹配成功的次数来反映匹配算法的性能.由于在实际测量中必然有噪声存在,为体现仿真的真实性,除试验1外,其余试验中的磁场仿真均加入标准差为5 nT的高斯白噪声.由于引入真实的磁传感器,故仿真试验也考虑了磁传感器自身的测量误差.地磁基准图选用我国境内高密度实测地磁场值,网格数目为60×60,网格间距为200 m×200 m,其等值线图如图 4所示.为表示方便,仿真试验中载体的坐标位置用地磁基准图中的网格坐标表示.
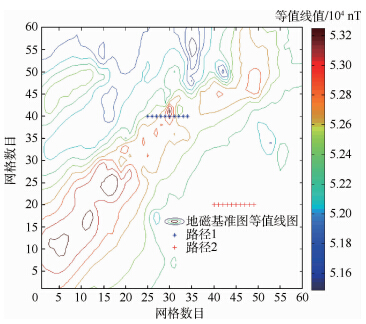 |
| 图 4 地磁基准图Fig. 4 Geomagnetic reference map |
| 图选项 |
3.1 测量噪声对匹配算法的影响针对测量噪声的影响,设计试验1:假设载体初始真实位置为(25,40),惯导指示初始位置与真实位置相差两个网格距离,坐标为(25,38),载体以100 m/s的速度自西向东匀速飞越匹配区域,飞行航迹如图 4中的路径1,惯导指示航向与实际飞行航向一致.电流每2 s改变一次,即每飞越一个网格点螺线管线圈模拟一次磁场值.匹配长度n=10,经计算,未添加噪声时该飞行路径上原始磁场数据的标准差为278.79 nT,加入零均值的高斯白噪声标准差为0~20 nT,仿真试验匹配结果如图 5所示.
 |
| 图 5 加入不同测量噪声的匹配结果Fig. 5 Matching results of different measurement noise |
| 图选项 |
从匹配结果可以发现,当噪声标准差为0~1 nT 时,能够全部匹配成功,说明算法在原理上是正确的,能够对惯导的偏差予以修正,但随着噪声的增加,匹配成功次数逐步下降,当噪声加大至9 nT 时,其成功次数急剧下降.可见测量噪声直接影响算法的匹配精度.
3.2 匹配长度对匹配算法的影响针对匹配长度的影响,设计试验2:匹配长度为6~20,其余条件与试验1一致,匹配结果如图 6所示.
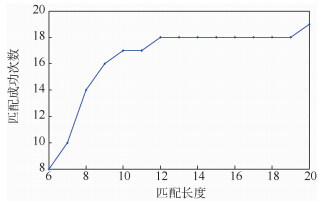 |
| 图 6 不同匹配长度的匹配结果Fig. 6 Matching results of different matching length |
| 图选项 |
从匹配结果可以发现,当匹配长度太小时,算法的匹配成功次数比较少,随着匹配长度的增加,匹配成功次数也随之增多,但是当匹配长度增加到12后,成功次数的增加就相对缓慢.针对该试验区域,ICCP算法匹配长度选为12比较合适.
3.3 匹配区域对匹配算法的影响针对匹配区域的影响,设计试验3:假设载体沿两条路径飞行,路径1同试验1中路径,路径2中载体初始真实位置为(40,20),惯导初始指示坐标为(40,18),如图 4所示.两条路径上其余条件与试验1一致,匹配结果如表 1所示.
表 1 不同匹配区域的匹配结果Table 1 Matching results of different matching region
| 匹配区域 | 匹配成功次数 |
| 路径1 | 18 |
| 路径2 | 0 |
表选项
从匹配结果可以发现,在其他条件相同的情况下,不同区域的匹配成功次数相差很大,这说明匹配区域的选择对算法有很大的影响.分析两条路径上的磁场信息,其磁场值的标准差分别为278.79 nT和3.61 nT,标准差越大,直观地反映了磁场的波动性和差异性越大,越有利于匹配.
3.4 惯导误差对匹配算法的影响惯导误差主要有两种:位置误差和航向误差.因此需要分别考虑两种误差对匹配算法的影响.
针对惯导位置误差的影响,设计试验4:载体真实位置坐标为(25,40),惯导指示初始位置横坐标为25,纵坐标为38~30,即惯导初始位置误差为2~10个网格距离,其余条件与试验1一致,匹配结果如图 7所示.
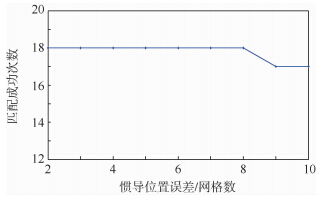 |
| 图 7 不同惯导位置误差的匹配结果Fig. 7 Matching results of different inertial navigation system (INS) position errors |
| 图选项 |
针对惯导航向误差的影响,设计试验5:惯导航向误差为0°~10°,其余条件与试验1一致,匹配结果如图 8所示.
 |
| 图 8 不同惯导航向误差的匹配结果Fig. 8 Matching results of different inertial navigation system (INS) heading errors |
| 图选项 |
从匹配结果可以发现,两种惯导误差对算法的影响权重不同:图 7数据表明,位置误差即使很大,依然具有很高的匹配成功概率,说明位置误差对算法的性能影响较小;图 8可以看出,当航向误差为3°以下时,匹配效果较好,航向误差在4°~7°时,成功次数迅速减少,而大于7°以后,成功次数几乎为0.由此可见,惯导航向误差对算法性能影响极大.
4 结 论本文通过建立地磁匹配导航半实物仿真系统,引入了磁场仿真环境和真实磁传感器,通过理论分析和半实物仿真试验对影响ICCP算法的因素进行了评估,仿真条件更加接近真实情况,结论更加可信.通过半实物仿真试验,得到以下结论:
1) ICCP算法原理是正确的,能够对惯导的偏差予以修正.但是其抗干扰性比较差,要想应用于工程实际中,必须建立较为精确的载体干扰磁场补偿模型以保证测量值的准确性.
2) 匹配长度对算法有影响,但并不是越大越好,在有限的匹配区域内,应综合考虑匹配成功概率和匹配次数,通过更接近实际情况的半实物仿真试验,做出折中的选择.
3) 匹配区域的选取对算法的性能影响较大.应尽量选取磁场差异性较大的地区作为匹配区域,以提高算法的抗干扰能力.
4) 惯导位置误差对算法的影响不是很明显,但惯导航向误差对算法影响较大,因此工程实际中应在保证航向误差不是很大的情况下使用该算法.
本文构建的地磁匹配导航半实物仿真系统是地磁匹配导航由理论走向工程应用的一个关键也是必经环节,在以后试验条件允许的情况下,系统中再加入等比例缩小的载体实物模型以及对应的载体干扰磁场补偿算法,结合实测得到的高精度地磁基准图,通过构建更为复杂和逼真的飞行磁场环境,进行半实物仿真试验,可以为算法的抗干扰能力、匹配长度的确定、匹配区域的选择以及惯导误差的影响做出进一步的有效的评估.
参考文献
| [1] | Wen Q Y, Kou Y M,Xia H W,et al.Advantages and drawbacks of applying vector decomposition to geomagnetic navigation systems[J].Control Engineering of China,2011,18(2):223-227. |
| Click to display the text | |
| [2] | Goldenberg F. Geomagnetic navigation beyond the magnetic compass[C]//2006 IEEE/ION Position,Location,and Navigation Symposium.Piscataway,NJ:IEEE,2006:684-694. |
| Click to display the text | |
| [3] | Zhao L, Zhang H,Chen L W.Research on geomagnetic-navigation-oriented geomagnetic field modeling methods[C]//Proceedings of 2010 Asia-Pacific International Symposium on Aerospace Technology.Xi'an:Northwestern Polytechnical University,2010:694-698. |
| Click to display the text | |
| [4] | Shorshi G, Bar-Itzhack I Y.Satellite autonomous navigation based on magnetic field measurement[J].Journal of Guidance,Control and Dynamics,1995,18(4):843-850. |
| Click to display the text | |
| [5] | 郭才发, 胡正东,张士峰,等.地磁导航综述[J].宇航学报,2009,30(4):1314-1319. Guo C F,Hu Z D,Zhang S F,et al.A survey of geomagnetic navigation[J].Journal of Astronautics,2009,30(4):1314-1319(in Chinese). |
| Cited By in Cnki (98) | Click to display the text | |
| [6] | 周莹莹, 张顺延,郭雷.地磁/惯性组合导航系统半物理仿真研究[J].控制工程,2011,18(增刊):15-17. Zhou Y Y,Zhang S Y,Guo L.Hardware-in-the-loop simulation of GNS/INS integrated navigation system[J].Control Engineering of China,2011,18(S1):15-17(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [7] | 单家元, 孟秀云,丁艳.半实物仿真[M].北京:国防工业出版社,2008. Shan J Y,Meng X Y,Ding Y.Hareware-in-the-loop simulation[M].Beijing:National Defense Industry Press,2008(in Chinese). |
| [8] | 李华. 激光制导信息场仿真关键技术研究[D].长沙:国防科学技术大学,2010. Li H.Key techniques research on laser guidance information fields simulation[D].Changsha:National University of Defense Technology,2010(in Chinese). |
| [9] | Yuan G N, Zhang H W,Yuan K F,et al.A combinational underwater aided navigation algorithm based on TERCOM/ICCP and Kalman filter[C]//Proceedings of the Fourth International Joint Conference on Computational Science and Optimization.Piscataway,NJ:IEEE Computer Society,2011:952-955. |
| Click to display the text | |
| [10] | Zhao J H, Wang S P,Wang A X.Study on underwater navigation system based on geomagnetic match technique[C]//ICEMI 2009-Proceedings of 9th International Conference on Electronic Measurement and Instruments.Piscataway,NJ:IEEE Computer Society,2009:3255-3259. |
| Click to display the text | |
| [11] | 黄斌,孙永荣, 王丽娜,等.地磁导航的迭代评价匹配算法[J].南京航空航天大学学报,2012,44(4):565-569. Huang B,Sun Y R,Wang L N,et al.Iterative evaluation matching algorithm for geomagnetic navigation[J].Journal of Nanjing University of Aeronautics & Astronautics,2012,44(4):565-569(in Chinese). |
| Cited By in Cnki (1) | |
| [12] | 杨勇,王可东, 吴镇,等.不同参数对地形等值线匹配算法精度影响的评估分析[J].航空学报,2010,31(5):996-1003. Yang Y,Wang K D,Wu Z,et al.Evaluation of performance of ICCP algorithm with different parameters[J].Acta Aeronautica et Astronautica Sinica,2010,31(5):996-1003(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [13] | 李素敏, 张万清.地磁场资源在匹配制导中的应用研究[J].制导与引信, 2004,25(3):19-21. Li S M,Zhang W Q. Study on the application of geomagnetic field contour in matching guidance[J].Guidance & Fuze,2004,25(3):19-21(in Chinese). |
| Cited By in Cnki (79) | Click to display the text | |
| [14] | 齐玮,王秀芳, 李夕海,等.基于统计建模的地磁匹配特征量选择[J].地球物理学进展,2010,25(1):324-330. Qi W,Wang X F,Li X H,et al.Selection of characteristic components for geomagnetic matching based on statistical modeling[J].Progress in Geophysics,2010,25(1):324-330(in Chinese). |
| Cited By in Cnki (13) | |
| [15] | 乔玉坤, 王仕成,张琪.地磁匹配特征量的选择[J].地震地磁观测与研究,2007,28(1):42-47. Qiao Y K,Wang S C,Zhang Q.Selection of the characteristic variable of geomagnetic for matching[J].Seismological and Geomagnetic Observation and Research,2007,28(1):42-47(in Chinese). |
| Cited By in Cnki (33) | Click to display the text |
