陈东明, 孙政平, 于开帅, 王冬琦
东北大学 软件学院, 辽宁 沈阳 110169
收稿日期：2020-03-26
基金项目：辽宁省自然科学基金资助项目(20170540320);辽宁省博士启动基金资助项目(20170520358);中央高校基本科研业务费专项资金资助项目(N2017010，N172415005-2)。
作者简介：陈东明(1971-)，男，安徽怀宁人，东北大学教授。

摘要：针对经典的节点相似性链路预测算法只考虑网络拓扑结构或者节点属性信息的问题, 使用词嵌入模型Word2vec学习得到节点文本属性信息的表示, 进而改进TADW(text-associated deep walk)算法, 弥补其语义信息表示能力的不足.基于改进的TADW图嵌入方法提出一种融合网络拓扑结构和节点属性信息的相似性指标, 并基于此相似性指标提出链路预测算法.在三个真实数据集上的实验结果表明所提出算法可以提高预测精度, 并具有更好的鲁棒性, 同时使用图嵌入的方法有效解决了网络数据的稀疏性问题.
关键词：TADW算法属性信息链路预测词嵌入Word2vec
Link Prediction Algorithm Based on Improved TADW
CHEN Dong-ming, SUN Zheng-ping, YU Kai-shuai, WANG Dong-qi
School of Software, Northeastern University, Shenyang 110169, China
Corresponding author: WANG Dong-qi, E-mail: wangdq@swc.neu.edu.cn.

Abstract: Aiming at the problem that the classic node similarity link prediction algorithm only considers the network topology or node attribute information, the word embedding model Word2vec to learn the representation of node text attribute information is employed, and then TADW(text-associated deep walk)algorithm for its insufficient ability to express semantic information is improved. Based on the improved TADW graph embedding method, a similarity index which incorporate the topological structure and node attribute information is proposed. Furthermore, the link prediction algorithm is proposed based on this similarity index. Experimental results on three real datasets demonstrate the superiority of the proposed algorithm with better robustness on predicting precision as well as network sparsity solvability.
Key words: TADW(text-associated deep walk)algorithmattribute informationlink predictionword embeddingWord2vec
链路预测(link prediction)是指根据已有的网络状态去预测网络中未产生连边的节点之间未来时刻产生连边的可能性^[1].它所要处理的是网络缺失信息的还原和网络未来信息的预测.所谓还原, 指的是网络中实际存在但尚未被发现的链路, 这种链路被称为未知链接(unknown links); 所谓预测, 指的是网络中当前不存在但未来有可能存在的链路, 这种链路被称为未来链接(future links).链路预测可以有效解决数据缺失和冗余问题, 例如噪声数据的处理、虚假连边识别等; 也可用于因网络规模过大、计算能力不足而进行的预测和筛选, 如蛋白质相互作用网络药物分子与靶细胞的结合预测、社交网络中的事件检测^[2]等.因此, 链路预测研究具有十分重要的理论意义和实际应用价值.
在链路预测研究中, 基于相似性的链路预测方法使用较多.该类方法最为简单高效, 适用于网络规模较大的情况.基本假设如下: 如节点之间的相似度越高, 那么此节点之间产生连边的可能性就越大^[3].目前主要分为三类: 第一类是基于网络节点的属性信息, 例如合作者网络中论文的题目、发表日期等信息.Lin^[4]依据信息论提出了相似性的普遍定义.傅颖斌等^[5]使用微博网络数据集, 采用随机森林的方法, 进而提出链路预测算法.许烁娜等^[6]提出的链路预测方法基于Skyline查询处理网络, 将经典方法预测得到的值作为节点属性值, 把Skyline点作为候选节点返回给目标用户.但是, 在实际研究中, 节点的属性信息大多是保密的, 获取难度比较大, 因此这类方法受到了一定限制.第二类是基于网络的拓扑结构信息, 相比于网络节点的属性信息, 网络拓扑结构信息相对容易获取而且可靠性高, 复杂度也低.刘冶等^[7]使用低秩和稀疏矩阵分解的方法, 融合多个数据源提出了具有健壮性的链路预测算法.在经典的基于网络结构信息的方法中, 基于局部信息相似性的算法因其时间复杂度较低且预测准确率高, 受到越来越多的关注^[8], 例如, 经典的共同邻居(common neighbors, CN)算法^[9].Yin等^[10]基于网络局部信息, 使用回归模型和决策树方法进行链路预测, 分析不同结构特性下用户间产生关注关系的可能性.基于网络结构的算法充分利用了网络的结构信息, 在静态网络链路预测中获得了良好的预测精度.黄立威等^[11]通过元路径(一组关系连接了多种节点类型的路径), 组合对象之间在不同元路径上建立连接的概率来进行链路预测.第三类是基于网络结构与节点属性融合的链路预测方法.Popescul等^[12]使用结构回归法建立预测模型, 使用CiteSeer搜索引擎中的数据进行实验.Backstrom等^[13]基于有监督随机游走的算法, 将网络结构中的节点和连边属性信息有效地融合起来.Ahmed等^[14]获得网络结构并抽取用户的属性信息, 对用户的社交关系进行建模, 进而提出链路预测算法.综上所述, 研究者对复杂网络中的链路预测研究不再仅仅从单方面考虑网络的拓扑结构或者属性信息, 而是综合考虑这两方面的信息.
现实世界中有许多节点多而连边数量却不多的网络, 这样的网络称为稀疏网络.网络的稀疏性问题给网络分析和预测带来许多困难, 需要得到有效解决^[15].近几年来, 使用深度学习的方式学习特征表示得到了越来越多的应用^[16].其中, 使用基于深度学习的Word2vec词嵌入模型^[17]处理文本的方式获得了很好的效果, 这也启发了研究者们在图嵌入方面的研究.图嵌入是将网络数据映射为低维向量的方法, 该方法能够有效地将网络数据输入到机器学习算法中.例如, 经典的Deepwalk模型, 它是学习网络中节点表示的代表性方法之一^[18].该模型参考Word2vec模型的思想, 首先通过随机游走得到节点的序列, 然后从随机游走的序列中获得网络的信息, 进而通过获取到的网络信息学习网络的节点表示.其中, 随机游走得到的节点序列相当于文本表示学习中的句子, 然后参考文本表示的方法处理网络中的数据.但是, Deepwalk仅仅针对网络的结构信息进行表示学习, 未考虑到网络的属性信息.文献[19]证明了深度随机游走算法等同于矩阵分解, 同时提出了一种融合网络属性信息的网络学习方法TADW(text-associated deep walk).
本文基于词嵌入模型Word2vec提出一种改进的TADW算法, 在此基础上提出一种融合网络拓扑结构和节点属性信息的链路预测算法, 可以有效提升包含语义信息的链路预测方法的准确性, 且具有较强的鲁棒性.
1 问题描述针对无向网络G(V, E), 其中V={v₁, v₂, …, v_n}, 表示该网络中的节点集合, E={ < v_x, v_y>, v_x, v_y∈V}, 表示该网络中的连边的集合.令|V|=n, n表示节点数量; |E|=m, m表示连边数量.令U表示网络G中所有节点对组成的边的全集, 则|U|=n(n-1)/2.使用某种链路预测算法, 计算每对没有连边的节点对(v_x, v_y)的联系.接着, 将所有未连接的节点对按照计算值的大小降序排序, 那么排在前面的节点对比排在后面的节点对相互连接的概率要大.
如果想要判断给定预测方法的准确性, 通常情况下将网络中现有的边E分为训练集E^T和测试集E^t, 显然E=E^T∪E^t, 并且E^T∩E^t=?.其中, 训练集用来计算节点对的值, 测试集用来衡量算法的性能.
定义1 ??已知边: 训练集E^T中的边.
定义2 ??不存在的边: 属于U但不属于E中的边.
定义3 ??未知边: 测试集E^t中的边和不存在的边的并集.
使用训练集训练网络G, 得到网络中所有节点对的值.如果给定的链路预测方法性能较好, 则网络G的“未知边”中测试集E^t中绝大多数节点对的值应大于“不存在的边”中节点对的值.
图 1给出了一个划分网络数据集的例子.图 1a是完整的网络, 该网络中有5个节点, 8条边.随机选择6条边作为该网络的训练集E^T, 如图 1b所示.剩余的两条边作为测试集E^t, 如图 1c所示.该网络中不存在的边为网络的全集U与网络现有的边E的差, 即2条, 如图 1d所示.使用某种链路预测算法, 计算得到所有未知节点对的相似度值, 其中包括测试集的2条边和不存在的边2条.之后将这4条边按照值从大到小排序, 如果更多的测试集中的边排在“不存在的边”的前面, 则表示该方法的预测效果较好.
图 1(Fig. 1)

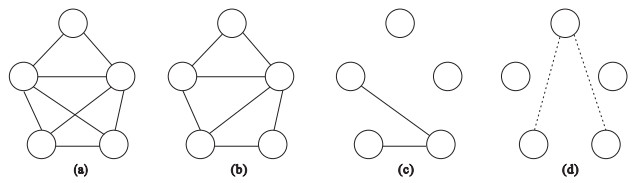图 1 网络数据集的划分Fig.1 Division of network dataset (a)—完整的网络；(b)—训练集；(c)—测试集；(d)—不存在的边.

2 算法设计与分析2.1 算法提出针对现实世界网络的大量外部信息和数据稀疏的特点, 本文提出以图嵌入的方法将网络结构和外部信息融合, 进而得到网络中每个节点的向量表示, 基于这种向量表示, 提出链路预测的相似性指标.
图嵌入的方法旨在对每个节点进行向量表示, 这种方法慢慢被认为是网络分析里很重要的一部分, 大多数方法都通过探讨网络结构来进行图嵌入.事实上, 网络节点也包含了很多信息, 但是却没有在典型的图嵌入中得到很好的利用.同时, 使用图嵌入的方法可以解决数据稀疏的问题, 它把每个节点表示为一个低维空间中的向量, 从而能够进行有效的计算.TADW是基于矩阵分解的方法将节点的文本信息引入到图嵌入中, TADW模型示意图如图 2所示.
图 2(Fig. 2)

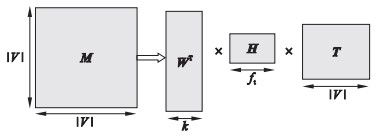图 2 TADW模型Fig.2 TADW model

该模型的目标函数如式(1)所示,

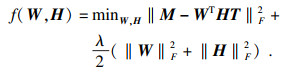(1)

模型把矩阵M分解成W, H, T这三个矩阵的乘积.其中, W和H表示参数矩阵, T表示文本的特征矩阵, 使用梯度下降的方法迭代更新参数矩阵W和H.TADW的目标是融合文本特征来获得整个网络信息的表示.
TADW算法的外部信息部分使用TF-IDF算法表示文本特征, 由于TF-IDF算法仅以词频度量词的重要性, 缺少对词位置信息的考虑, 因此无法反映序列信息, 难以有效挖掘深层语义信息, 这就造成了网络中语义信息的大量丢失.
本文对TADW中的特征矩阵T进行改进, 使用词嵌入模型对外部信息进行计算.使用网络节点特征作为语料, 训练得到Word2vec模型, 获得模型中单词的向量表示, 从而计算特征矩阵.然后使用TADW模型框架进行训练, 得到节点的向量表示后进行多分类评价, 使用节点向量提出链路预测的相似性指标.
2.2 相似性指标的计算通过改进TADW算法, 得到网络中每个节点的向量表示.在空间中, 两个向量之间距离越近, 它们之间的相似度就越高.本文中使用欧氏距离衡量两个向量间的距离大小.下面定义的相似性指标为基于Word2vec训练模型.
定义4 ??WTADW相似性指标: 使用Word2vec模型训练特征矩阵.用S_WTADW表示节点为v_x和v_y的相似性值, 定义如公式(2)所示,

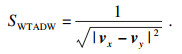(2)

其中: v_x表示节点v_x的向量; v _y表示节点v_y的向量; 表示节点v_x和节点v_y的欧氏距离.取距离的倒数, 即两节点间距离越大, 相似性值S_WTADW越小; 两节点间的距离越小, 相似性值S_WTADW越大.
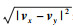
2.3 算法过程描述基于2.2节定义的WTADW指标, 提出了基于改进TADW的链路预测算法(link prediction algorithm based on improved TADW, LPIT).为了使算法具有普适性, 本文算法使用无向无权静态社交网络, 见算法1.
算法1
输入: 无向无权网络G(V, E)
输出: 评价指标值
1) 读取网络G(V, E), 构建网络邻接矩阵N;
2) 将E划分为训练集E^T和测试集E^t.使用K折交叉验证的方式划分数据集, 其中K取10;
3) 对于训练集和测试集中的节点对, 计算图嵌入得到节点对之间的欧氏距离, 进而得到节点对的相似性指标.对比的相似性指标names={‘WTADW’, ‘CN’, ‘JC’, ‘AA’, ‘RA’, ‘PA’, ‘SR’};
4) 构建节点对的相似性矩阵S;
5) 计算算法的评价指标AUC(接受者操作特性曲线下方的面积)的值.
3 实验分析本文研究选取3个真实网络数据集.
1) DBLP(digital bibliography & library project)^[20].DBLP数据集是计算机类英文文献的集成数据库系统, 它按照年代列出了作者的科研成果.储存的相关元数据有: 作者、标题、发表日期等.本文选取DBLP数据集中的前三个类型的期刊数据.
2) Cora^[21].Cora数据集包括2 708条科学出版物, 分为7类.引文网络由5 429条链接组成.数据集中的每个出版物都由一个0/1值的单词向量来描述, 该向量表示字典中相应单词是否存在.
3) CiteSeer^[22].CiteSeer数据集包括3 312条科学出版物, 分为6类.引文网络由4 732条链接组成.与Cora数据集相同, CiteSeer数据集中的每个出版物都由一个0/1值的单词向量来描述, 该向量表示字典中相应单词是否存在.表 1为上述三个数据集的统计特征.
表 1(Table 1)

表 1 数据集的统计特征Table 1 Statistic characteristic of datasets 数据集 节点 连边 类别 DBLP 3577 5254 3 Cora 2708 5429 7 CiteSeer 3312 4732 6

表 1 数据集的统计特征 Table 1 Statistic characteristic of datasets

3.1 图嵌入实验选择节点的多分类问题去评价图嵌入的质量, 选择SVM用于监督学习和测试.以节点的向量表示作为特征来训练分类器, 用不同的训练率来评估分类的准确性, 训练率从10 % 到90 % 不等.对于每个训练率, 随机选择文档作为训练集, 其余的文档作为测试集.重复实验10次, 最后得到平均准确度.
表 2~表 4分别展示了所提出算法在DBLP，Cora和CiteSeer三个数据集上的分类表现.其中, WTADW表示使用Word2vec模型训练特征矩阵得到向量表示.
表 2(Table 2)

表 2 DBLP数据集的评价结果Table 2 Evaluation results on DBLP dataset 训练比率/% 10 20 30 40 50 60 70 80 90 WTADW 0.944 4 0.949 7 0.951 4 0.952 4 0.954 1 0.952 2 0.953 1 0.953 8 0.961 8 TADW 0.824 5 0.843 0 0.854 1 0.859 0 0.852 1 0.861 3 0.861 4 0.859 4 0.869 4

表 2 DBLP数据集的评价结果 Table 2 Evaluation results on DBLP dataset

表 3(Table 3)

表 3 Cora数据集的评价结果Table 3 Evaluation results on Cora dataset 训练比率/% 10 20 30 40 50 60 70 80 90 WTADW 0.792 4 0.814 9 0.825 4 0.825 2 0.844 1 0.852 3 0.873 3 0.870 8 0.878 2 TADW 0.605 0 0.634 0 0.631 3 0.619 6 0.637 3 0.630 0 0.624 8 0.608 8 0.575 6

表 3 Cora数据集的评价结果 Table 3 Evaluation results on Cora dataset

表 4(Table 4)

表 4 CiteSeer数据集的评价结果Table 4 Evaluation results on CiteSeer dataset 训练比率/% 10 20 30 40 50 60 70 80 90 WTADW 0.686 0 0.692 8 0.697 7 0.706 7 0.704 1 0.715 4 0.716 2 0.707 3 0.716 8 TADW 0.679 3 0.681 5 0.682 1 0.682 0 0.688 4 0.689 8 0.687 1 0.681 7 0.683 7

表 4 CiteSeer数据集的评价结果 Table 4 Evaluation results on CiteSeer dataset

由表 2~表 4看出, 本文提出的算法在DBLP和Cora数据集上的分类结果大幅领先TADW, 在CiteSeer数据集上相比TADW也有一定提升, 在三个数据集上的表现均优于TADW算法.这些实验结果验证了本文提出的WTADW算法对网络节点的高质量表示.
3.2 图嵌入实验参数灵敏度分析对本实验中两个超参数维数k和正则化项的权重λ, 在此讨论超参数设置对本实验的影响程度.用不同的k和λ对分类精度进行测试, 设置k从40到120不等, λ从0.1到1不等.
图 3表示在DBLP, Cora和CiteSeer数据集上使用Word2vec模型训练特征矩阵的准确度(参数灵敏度)折线.
图 3(Fig. 3)

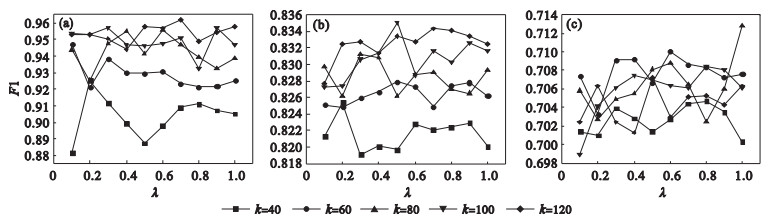图 3 参数灵敏度折线图Fig.3 Parameter sensitivity line chart (a)—DBLP; (b)—Cora; (c)—CiteSeer.

从图 3可以看出, 当k值不变时, λ从0.1到1的范围内变化的F1值浮动较小; 当λ不变, k≥80时, 本文提出方法的准确度较高.因此, 当k和λ在合理范围内变化时, WTADW可以保持稳定, 具有较强的鲁棒性.
3.3 链路预测实验结果分析在保证了本文提出的图嵌入方法的有效性和鲁棒性后, 接着进行本文提出的WTADW指标与改进前的TADW及经典的相似性指标的链路预测对比实验.其中, 链路预测的评价指标AUC的计算方法^[23]为, 若测试集中的边的分数值大于不存在的边的分数值, 加1分, 若两个分数相等, 加0.5分, 如公式(3)所示,

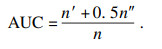(3)

其中: n为独立比较次数; n′为测试集中的边的分数值大于不存在的边的分数值的次数; n″为分数相等的次数.
表 5是本文提出的链路预测的相似性指标与TADW及经典的链路预测相似性指标的对比实验结果.
表 5(Table 5)

表 5 三个数据集上不同指标的AUC比较Table 5 AUC comparison on three datasets with different index 数据集 WTADW TADW CN JC AA RA PA SR DBLP 0.991 4 0.975 1 0.522 3 0.522 3 0.522 3 0.522 3 0.191 1 0.032 3 Cora 0.984 7 0.880 4 0.546 2 0.546 5 0.546 5 0.546 5 0.175 8 0.253 3 CiteSeer 0.995 5 0.931 7 0.538 7 0.538 7 0.538 7 0.538 7 0.205 2 0.178 6

表 5 三个数据集上不同指标的AUC比较 Table 5 AUC comparison on three datasets with different index

由表 5可知, 在DBLP, Cora和CiteSeer数据集中, 本文提出的WTADW指标都优于经典的CN, JC, AA, RA, PA和SR指标, 且优于改进前的TADW.在Cora数据集上, WTADW相较TADW有约10%的提升, 在TADW的AUC值已经达到90%以上的DBLP和CiteSeer数据集上, WTADW相较TADW仍有提升.在三个数据集上, TADW均已经达到了较高的AUC值, 而本文所提出的WTADW指标相比TADW仍能够有所提升, AUC值接近100%, 这应当与节点标签的属性信息有关, 由于节点标签的相似性为算法的高准确率提供了保障, 因此使用TADW即可获得较高的AUC值, 而WTADW相较TADW能够更加有效地学习网络特征, 因此获得了更高的AUC值.
通过与经典相似性指标的对比实验, 可以看出，使用网络拓扑结构和网络节点属性相融合的方式能更加充分地学习到网络中的信息.同时, 使用图嵌入方法对网络进行表征学习也更有效地表示了网络信息, 解决了网络数据的稀疏性问题.
3.4 特征扰动实验结果分析为了进一步验证本文所提出算法的鲁棒性, 对本文所提出算法进行特征扰动实验, 比较两组结果在节点分类和链路预测任务上的差异.特征扰动策略为随机修改或删除部分节点的属性信息, 扰动范围为0到0.95不等.实验结果如图 4~图 6所示.
图 4(Fig. 4)

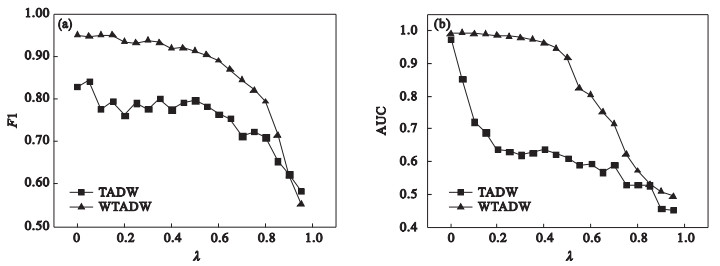图 4 DBLP数据集上扰动比例灵敏度折线图Fig.4 Disturb ratio sensitivity line chart on DBLP dataset (a)—F1值随扰动比例变化；(b)—AUC值随扰动比例变化.

图 5(Fig. 5)

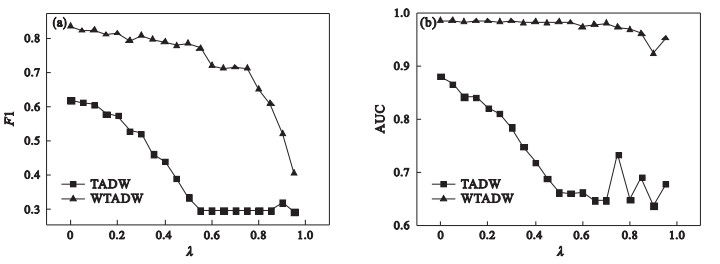图 5 Cora数据集上扰动比例灵敏度折线图Fig.5 Disturb ratio sensitivity line chart on Cora dataset (a)—F1值随扰动比例变化；(b)—AUC值随扰动比例变化.

图 6(Fig. 6)

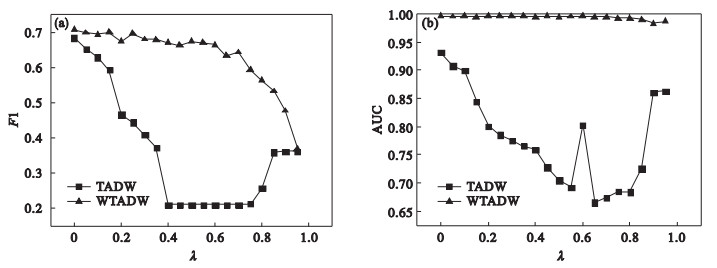图 6 CiteSeer数据集上扰动比例灵敏度折线图Fig.6 Disturb ratio sensitivity line chart on CiteSeer dataset (a)—F1值随扰动比例变化；(b)—AUC值随扰动比例变化.

由图 4~图 6可知, 在DBLP数据集上, 随着扰动比例的增加, WTADW和TADW的F1值与AUC值均逐渐下降, 而WTADW表现始终优于TADW, 且AUC值的变化更加平稳, 当扰动比例趋近100%时, WTADW与TADW表现也渐渐趋同; 在Cora和CiteSeer数据集上, 分类任务的F1值变化规律与DBLP数据集上表现相同, WTADW的变化更加平稳, 而在链路预测任务上的表现, WTADW与TADW均未因特征扰动受到较大影响, WTADW表现始终优于TADW.在三个真实网络数据集上, WTADW的表现始终优于TADW, 且在特征扰动下的变化更加平稳, 证明了本文所提出算法的鲁棒性.
4 结语针对基于矩阵分解的图嵌入算法TADW存在的缺点, 提出一种融合网络拓扑结构信息和节点属性信息的图嵌入方法, 设计一种相似性指标WTADW, 基于所提出的相似性指标提出了链路预测算法.在三个真实网络数据集上的实验结果验证了本文提出的链路预测算法比TADW算法具有更好的预测效果, 证明了融合网络拓扑信息和节点属性信息可以提高预测精度, 并且使用图嵌入方法解决了网络数据的稀疏性问题.
参考文献

[1]	Lyu L, Zhou T. Link prediction in complex networks: a survey[J]. Physica A: Statistical Mechanics & Its Applications, 2011, 390(6): 1150-1170.
[2]	胡文斌, 彭超, 梁欢乐, 等. 基于链路预测的社会网络事件检测方法[J]. 软件学报, 2015, 26(9): 2339-2355. (Hu Wen-bin, Peng Chao, Liang Huan-le, et al. Event detection method based on link prediction for social network evolution[J]. Journal of Software, 2015, 26(9): 2339-2355.)
[3]	Daminelli S, Thomas J M, Durán C, et al. Common neighbours and the local-community-paradigm for topological link prediction in bipartite networks[J]. New Journal of Physics, 2015, 17(11): 113037. DOI:10.1088/1367-2630/17/11/113037
[4]	Lin D. An information-theoretic definition of similarity[J]. Icml, 1998, 98(1998): 296-304.
[5]	傅颖斌, 陈羽中. 基于链路预测的微博用户关系分析[J]. 计算机科学, 2013, 41(2): 201-205. (Fu Ying-bin, Chen Yu-zhong. Relationship analysis of microblogging user with link prediction[J]. Computer Science, 2013, 41(2): 201-205.)
[6]	许烁娜, 曾碧卿. 基于Skyline查询的社会网络链接预测[J]. 计算机科学, 2014, 42(1): 264-267. (Xu Shuo-na, Zeng Bi-qing. Skyline based link prediction on social networks[J]. Computer Science, 2014, 42(1): 264-267.)
[7]	刘冶, 朱蔚恒, 潘炎, 等. 基于低秩和稀疏矩阵分解的多源融合链接预测算法[J]. 计算机研究与发展, 2015, 52(2): 423-436. (Liu Ye, Zhu Wei-heng, Pan Yan, et al. Multiple sources fusion for link prediction via low-rank and sparse matrix decomposition[J]. Journal of Computer Research and Development, 2015, 52(2): 423-436.)
[8]	Yuan G, Murukannaiah P K, Zhang Z, et al. Exploiting sentiment homophily for link prediction[C]// 8th ACM Conference on Recommender Systems. Foster City: ACM, 2014: 17-24.
[9]	Igor R, Maxim Z. The distribution of the maximum number of common neighbors in the random graph[J]. arXiv Preprint arXiv, 2018, 1804: 04430.
[10]	Yin D, Hong L, Davison B D. Structural link analysis and prediction in microblogs[C]//Proceedings of the 20th ACM International Conference on Information and Knowledge Management. Glasgow, 2011: 1163-1168.
[11]	黄立威, 李德毅, 马于涛, 等. 一种基于元路径的异质信息网络链路预测模型[J]. 计算机学报, 2014, 37(4): 848-858. (Huang Li, Li De-yi, Ma Yu-tao, et al. A meta path-based link prediction model for heterogeneous information[J]. Chinese Journal of Computers, 2014, 37(4): 848-858.)
[12]	Popescul A, Ungar L H. Structural logistic regression for link analysis[J]. Departmental Papers(CIS), 2003, 133: 1-19.
[13]	Backstrom L, Leskovec J. Supervised random walks: predicting and recommending links in social networks[C]//Proceedings of the Fourth ACM International Conference on Web Search and Data Mining. Boston, 2011: 635-644.
[14]	Ahmed C, El Korany A. Enhancing link prediction in Twitter using semantic user attributes[C]//2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining(ASONAM). Paris: IEEE, 2015: 1155-1161.
[15]	Getoor L. Link mining: a new data mining challenge[J]. ACM SIGKDD Explorations Newsletter, 2003, 5(1): 84-89. DOI:10.1145/959242.959253
[16]	孙志远, 鲁成祥, 史忠植, 等. 深度学习研究与进展[J]. 计算机科学, 2016, 43(2): 1-8. (Sun Zhi-yuan, Lu Cheng-xiang, Shi Zhong-zhi, et al. Research and advances on deep learning[J]. Computer Science, 2016, 43(2): 1-8.)
[17]	Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[J]. Advances in Neural Information Processing Systems, 2013, 26: 3111-3119.
[18]	Perozzi B, Al-Rfou R, Skiena S. Deepwalk: online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 701-710.
[19]	Yang C, Liu Z, Zhao D, et al. Network representation learning with rich text information[C]//Twenty-Fourth International Joint Conference on Artificial Intelligence. Buenos, 2015: 2111-2117.
[20]	DBLP. Dblp dataset[DB/OL]. (2020-03-26)[2019-11-22]. https://dblp.uni-trier.de/xml/.
[21]	Cora. Cora datasets[DB/OL]. (2020-03-26)[2015-01-01]. https://linqs.soe.ucsc.edu/data/.
[22]	CiteSeer. CiteSeer dataset(2020-03-26)[2015-01-01]. https://linqs.soe.ucsc.edu/data/.
[23]	吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(5): 651-661. (Lyu Lin-yuan. Link prediction on complex networks[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(5): 651-661. DOI:10.3969/j.issn.1001-0548.2010.05.002)