试卷五
试题五
|
一、判断题 |
|
|
1 .×
|
|
|
2 .√ |
|
|
3 .√
|
|
|
4 .√
|
|
|
5 .× |
|
|
6 .× |
|
|
7 .√ |
|
|
8 .× |
|
|
9 .√ |
|
|
10.√ |
|
| 二、单项选择题 | |
|
1 .③ |
|
|
2 .② |
|
|
3 .② |
|
|
4 .① |
|
|
5 .③ |
|
|
6 .③ |
|
|
7 .① |
|
|
8 .② |
|
|
9 .④ |
|
|
10.④ |
|
|
|
||
| 三、填空题 | ||
|
1 .12 |
||
|
2 .65.96 % |
||
|
3 .(0.925,0.975) |
||
|
4 .0.5 |
||
|
5 .16.61;0.238 |
||
|
6 .16.71% |
||
|
7 .a>c>b |
||
|
8 .标准正态分布 |
||
|
9 .0.01 |
||
|
10. 样本指标 、 全及指标 |
||
| 四、问答题 | ||
|
1. 答: |
||
|
总体总量即总体单位数,它是由每个总体单位加总而得到的。它可以反映总体规模的大小。 |
||
|
标志总量是指总体各单位某一数量标志值的总和,它是反映总体某一方面特征的总数量。 |
||
|
一个总量指标到底是属于总体总量还是标志总量,并不是固定不变的,它随着研究目的的不同而变化。研究目的变了,总体和总体单位、总体总量和标志总量就会随之而变。 |
||
| 2. 答: | ||
| 抽样调查是指从研究的总体中按随机原则抽取部分单位作为样本,进行观察研究,并根据这部分单位的调查结果去推断总体,以达到认识总体的统计调查方法。 | ||
|
特点: |
||
|
( 1 )抽样调查是一种非全面调查。 |
||
| ( 2 )是按随机原则抽取调查单位。 | ||
| ( 3 )是用总体中部分单位的指标数值去推断总体指标数值。 | ||
| ( 4 )抽样调查中产生的误差可以事先计算并加以控制。 | ||
| 作用: | ||
| ( 1 )用于不可能进行全面调查的总体数量特征的推断。 | ||
| ( 2 )用于某些不必要进行全面调查的总体数量特征的推断。 | ||
| ( 3 )用于全面调查资料的评价和验证。 | ||
| ( 4 )用于生产过程的质量控制。 | ||
| 3. 答: | ||
| 趋势直线模型的配合条件是:当时间数列散点图表现为直线趋势,其数据的一阶差分近似一常数时可配合趋势直线模型。 | ||
|
指数曲线模型的配合条件是:当时间数列对数散点图表现为直线趋势,其数据对数的一阶差分近似一常数时或其环比发展速度近似一常数时可配合指数曲线模型。 |
||
|
二次抛物线模型的配合条件是:当时间数列散点图围绕上凹的上升或下凹的上升曲线趋势波动,其数据的逐期增长量之差(第二阶差)近似一个常数时,可配合趋势二次抛物线模型。 |
||
| 4. 答: | ||
| 有两种方法计算时间数列的平均发展速度指标,即水平法和累计法。 | ||
|
( 1 )水平法是指从最初水平出发,按照此法计算的平均发展速度所推算出来的最末水平,应等于实际最末水平,称水平法。由于各个时期环比发展速度的连乘积等于总发展速度,因此,平均发展速度可以用各个时期环比发展速度连乘积开项数次方来计算。这种形式的平均数称几何平均数,因此水平法也称几何平均法。 |
||
|
( 2 )累计法是指从最初水平出发,按照此法计算的平均发展速度所推算出来的各期发展水平的总和,应等于各期实际发展水平的累计数,称为累计法。这种方法,是利用解一元高次方程式求平均速度的方法,因此,也称方程式法。 |
||
| 两种计算方法的侧重点不同,应根据研究对象的不同特点来选用。对于侧重于考察最末一年所达到水平的计划指标,宜选用水平法计算平均发展速度。对于侧重于考察整个发展阶段内应达到的累计总量的计划指标,则宜选用累计法计算平均发展速度。 | ||
|
|
||
| 五、计算题: | ||
| 1. 解: | ||
| 平均亩产量的变动为: | ||
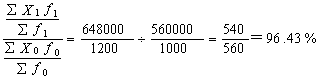 |
||
 |
||
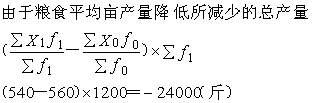 |
||
 |
||
| 三者的关系如下: | ||
| 96.43 %= 89.29 %× 108 % | ||
|
-24000 =( -72000 ) +48000 |
||
| 2. 解: | ||
| 平均发展速度 | ||
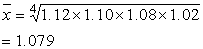 |
||
| 3. 解: | ||
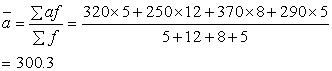 |
||
| 4. 解: | ||
设该校初三学生的语文水平为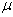 . . |
||
|
|
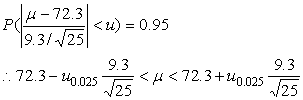 |
|
所以 , 该校初三学生的语文水平的 95% 的置信区间为 :68.65< 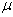 <75.95 <75.95 |
||
|
5. 解: |
||
 |
||
