删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

暨南大学《统计学》中文真题试题试卷含答案四

暨南大学 /2011-11-25

试卷四

（一）判断题
 
1、 统计一词包含统计学、统计资料等二种涵义。（ ）
是: 否:
2、 调查单位和填报单位既可以一致，也可以不一致。（ ）
是: 否:
3、 统计分组的关键问题是确定分组标志。 （ ）
是: 否:
4、 抽样极限误差总是大于抽样平均误差。（ ）
是: 否:
5、 甲产品产量与单位成本的相关系数是－0.985，乙产品单位成本与利润的相关系数是＋0.985。因此，乙比甲的相关程度高。（ ）
是: 否:
6、 中位数和众数不受极端数值的影响。 （ ）
是: 否:
7、 统计误差可以计算并加以控制。 （ ）
是: 否:
8、 在直线回归分析中，两个变量是对等的，不需要区分因变量和自变量。 （ ）
是: 否:
9、 加权指数是计算总指数广为采用的方法，个体指数也是一种加权数。 （ ）
是: 否:
10、 当直线相关系数 r ＝ 0 时，说明变量之间不存在任何相关关系。 （ ）
是: 否:
 
（二） 单项选择题
 
1、 一个统计总体（ ）

①只能有一个标志
②只能有一个指标
③可以有多个标志
④可以有多个指标
 
 
2、 下列指标属于结构相对数的是 （ ）

① 计划完成相对数
② 工业产值占工农业总产值的比重
③ 百元流动资金利润率
产值资金占用率
 
 
3、 如果变量数列中，有一项变量值为 0 ，则不能计算 （ ）

① 算术平均数
② 几何平均数
③ 众数
④ 中位数
 
 
4、 在相关分析中，用于判断两个变量之间相关关系类型的图形是 （ ）

① 直方图
② 散点图
③ 次数分布多边形图
④ 累计频率曲线图
 
 
5、 某地区粮食产量的环比增长速度， 1999 年为 3 ％， 2000 年为 5 ％，则 1999-2000 年该地区粮食产量共增长了 （ ）

① 2 ％
② 8 ％
③ 8.15 ％
④ 15 ％
 
 
6、 下面四个动态数列中，属时点数列的是 （ ）

① 历年招生人数动态数列
② 历年增加在校生人数动态数列
③ 历年在校生人数动态数列
④ 历年毕业生人数动态数列
 
 
7、 按指数的性质不同，指数可分为 （ ）

① 个体指数和总指数
② 简单指数和加权指数
③ 数量指标指数和质量指标指数
④ 动态指数和静态指数
 
 
8、 两名医生为学生体检，甲医生每小时检 15 人，乙医生每小时检 20 人，则平均每人每小时体检学生（ ）人。

① 17.32
② 17.50
③ 17.14
④ 17.83
 
 
9、 一个企业产品销售收入计划增长 8 ％，实际增长 20 ％，则计划超额完成程度为 （ ）

① 12 ％
② 150 ％
③ 111.11 ％
④ 11.11 ％
 
 
10、 下列等式中，不正确的是 （ ）

① 发展速度＝增长速度＋ 1
② 定基发展速度＝相应各环比发展速度的连乘积
③ 定基增长速度＝相应各环比增长速度的连乘积
④ 平均增长速度＝平均发展速度－ 1
 
 
（三）填空题
 
1、在显著性检验中，如果我们得到的结论越可靠，则所取的显著性水平 a 的值就要________ 。
a.
2、 随机抽取 100 名高中生进行调查，发现近视率达到 72% ，若根据这个样本估计，高中生近视率置信区间的上限为 83.6% ，则用来估计这个置信区间的置信度为______。
a.
3、 在组距数列中，表示各组界限的变量值称为 _________ ，各组上限与下限之间中点位置的值称为 _________ 。
a.
b.
4、 按所反映的时间不同，总量指标可以分为 _________ 和 _________ 。
a.
b.
5、 某市 1993～1997 年在职教师的人数分别为7258，8105 ，8823 ，9107 和9215 人，若按这种增长速度增长，则1998年该市的在职教师的人数将达到______人。
a.
6、 在单总体相关系数的假设检验中，若查表检验时的自由度为28 ，则样本的容量 n=_______。
a.
7、 平均发展速度的计算有___________________和______________________两种方法。
a.
b.
8、 制定统计调查方案的首要问题是 ________________________。
a.
9、相关关系按相关方向的不同，分为 _________ 和 _________ 。
a.
b.
10、标准正态分布曲线的原点所对应的原始分 X=__________ ，标准分 Z= ________ 。
a.
b.
 
(四）简答题
 
1、 相对指标有哪几种？
 

2、 定基发展速度和环比发展速度的关系如何？
 
3、 什么是时期数列和时点数列？两者有什么特点和区别？
 
4、 抽样实际误差、抽样平均误差和抽样极限误差有何联系与区别？
 
（四）计算题
 
1、 某产品情况如下表所示：
等级
单价（元 / 斤）
收购额（元）

一级品

二级品

三级品

1.20

1.05

0.90

2400

3150

3600
 		  
请计算产品的平均收购价格 。  
a.
 
2、 1989-1994 年广东省实际利用外资总额如下，请填表。 ：
年 份
1989
1990
1991
1992
1993
1994

实际利用外资总额（万美元）
239915
202347
258250
486147
965225
1144665

逐期增减量

            

累积增减量

            

环比发展速度

            

定基发展速度

            

环比增减速度

            

定基增减速度

            

增减 1 ％的绝对值

            
 
   
3、 某地区1995年底人口数为2000万人，假定以后每年以9‰的增长率增长；又假定该地区1995年粮食产量为120亿斤，要求到2000年平均每人粮食达到800斤，请计算2000年粮食产量应该达到多少？粮食产量每年平均增长速度如何？
a.  
b.
 
4、 某市教育局为评估甲、乙两所学校的数学教学水平，现从两所学校的学生中各随机抽取 40 名学生进行测验，测验结果甲校学生的平均分为 82.3 分，标准差为 9.2 分；乙校学生的平均分为 80.8 分，标准差为 10.1 分。问甲、乙两校英语的教学水平是否存在差异？ ( a =0.10)
a.
 
5、 某地区 1994 年至 2000 年工业总产值资料如下：

年份

1994

1995

1996

1997

1998

1999

2000

工业总产值（万元）

180

200

208

214

220

233

241
试用最小平方法配合趋势直线模型，并测定各年的长期趋势值。
a.

一、判断题

  
1 ．×  

2 ．√

  
3 ．√  
4 ．×  

5 ．×

  

6 ．√

  

7 ．√

  

8 ．×

  

9 ．√

  

10．×

  
 
二、单项选择题

1 ．④

  

2 ．②

  

3 ．②

  

4 ．②

  

5 ．③

  

6 ．③

  

7 ．①

  

8 ．②

  

9 ．④

  

10．③

  
   
三、填空题

1 ．小

2 ．0.01

3 ．组限、组中值

4 ．时期指标、时点指标

5 ．9020

6 ．30

7 ．水平法、累计法

8 ．明确调查的任务和目的

9 ．正相关、负相关

10.平均分、零
 
四、问答题

1. 答：

  
根据统计研究的目的和任务的不同，相对指标可分为计划完成相对数、结构相对数、比例相对数、比较相对数、动态相对数和强度相对数六种。
计划完成相对数是计划期内实际完成数与计划数对比的比值；

结构相对数是总体中某部分数值与该总体数值对比的比值；

比例相对数是同一总体某一部分数值与另一部分数值对比的比值；

比较相对数是同一时间的同类指标在不同空间对比的比值；

动态相对数是某一社会经济现象在不同时期两个数值对比的比率；

强度相对数是两个性质不同而又有联系的指标对比的比率。
 
2. 答：  
（1）定基发展速度等于相应时期内各个环比发展速度的连乘积：

（2）相邻两个定基发展速度之商等于相应的环比发展速度：

  

 

  
3. 答：  
时期数列是指由反映某种社会经济现象在一段时期内发展过程累计量的总量指标所构成的绝对数时间数列。  

时点数列是由反映某种现象在一定时点上的发展状况的总量指标所构成的绝对数时间数列。

  

两种的特点与区别在于：

  
（1） 时期数列中各项指标值反映现象在一段时期内发展过程的总量；各项指标值随着现象的发展进程进行连续登记，因而各项指标值可以相加，相加后的指标值反映现象在更长时期内发展过程的总量；每项指标值的大小与其所包括的时期长短有直接关系，时期长，指标值大，时期短，指标值小，因此，其时期间隔一般应该相等。  
（2）时点数列中各项指标值反映现象在一定时点上的发展状况，各项指标值一般按时点所表示的瞬间进行不连续登记，相加无实际经济意义，因而不能直接相加；各项指标值的大小与其时点间隔的长短没有直接关系，因而其时点间隔不要求必须相等。  
 
4. 答：

发展水平是指时间数列中的每一项具体指标值。

  
增长量是指时间数列中计算期水平与基期水平之差。  
平均增长量是指逐期增长量的简单算术平均数，说明现象在一般较长时间内，平均每期增减变化的数量。  
发展速度是计算期发展水平与基期发展水平之比，说明计算期水平发展达到基期水平的若干倍或百分之几，反映了某种社会经济现象在一定时期内发展的方向和程度。  
增长速度是计算期增长量对基期发展水平之比，说明社会经济现象在一定时期内增减程度。  
增长百分之一的绝对值是指在环比增长速度中，计算期发展水平比前期发展水平每增长百分之一所增长的绝对数。  

 

  
五、计算题：
1. 解：
 
 
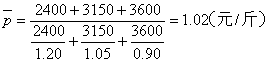2. 解：
 

年 份

1989

1990

1991

1992

1993

1994

实际利用外资总额（万美元）

239915

202347

258250

486147

965225

1144665

逐期增减量

－

-37568

55903

227897

479078

179440

累积增减量

－

-37568

18335

246232

725310

904750

环比发展速度
－

0.843

1.276

1.882

1.985

1.186

定基发展速度
－

0.8434

1.076

2.026

4.023

4.77

环比增减速度
－

-0.156

0.276

0.882

0.985

0.186

定基增减速度
－

-0.156

0.076

1.026

3.023

3.77

增减1％的绝对值
－

2399.15

2023.47

2582.5

4861.47

9652.25
 
3. 解：
  2000 年底人口数＝ 2000 ×（ 1 ＋ 0.009 ） 5 ＝ 2054.49 （万元）
  2000 年粮食总产量＝ 800 × 2054.5 ＝ 1643589.97 （万斤）
  设粮食每年增长速度为 x ，则：
 

1200000 ×（ 1 ＋ x ） 5 ＝ 1643589.97

 

 所以， x ＝ 6.49 ％
4. 解：
 
 
5. 解：
 

年份 t

年次 x

工业总产值 yt

xy

x2

趋势值 Tt

1994

1995

1996

1997

1998

1999

2000

-3

-2

-1

0

1

2

3

180

200

208

214

220

233

241

-540

-400

-208

0

220

466

723

9

4

1

0

1

4

9

185.75

195.07

204.39

213.71

223.04

232.36

241.68

合计

0

1496

261

28

1496

将上表合计栏资料代入联立方程：
 

 

 得趋势直线模型为：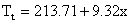

 

 将各年年次代入模型，即可求得各年趋势值，填入上表。

相关话题/统计学

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.