

1. 军事科学院军事医学研究院 微生物流行病研究所,北京 100071;
2. 病原微生物生物安全国家重点实验室,北京 100071
收稿日期:2020-07-04;接收日期:2020-10-16;网络出版时间:2020-10-22
摘要:随着高性能计算需求的不断增长,传统计算模式面临着前所未有的巨大挑战。在众多新兴计算技术中,DNA计算系统以其低能耗、并行化等特点而广受关注。DNA电路(DNA circuit) 是实现DNA计算的基础,也是该领域重要的分子信息调控和处理技术。文中重点介绍了DNA计算的基本原理,并总结了最新的研究进展,最后讨论了基于DNA计算所面临的挑战。此类集成的分子计算系统有望广泛应用于航空航天、信息安全及国防建设等领域。
关键词:DNA电路DNA计算DNA链置换技术基因线路DNA芯片
The current status and future prospects of DNA computing
Shan Yang1,2, Jinyu Li1,2, Yujun Cui1,2, Yue Teng1,2


1. Beijing Institute of Microbiology and Epidemiology, Academy of Military Medical Sciences, Beijing 100071, China;
2. State Key Laboratory of Pathogen and Biosecurity, Beijing 100071, China
Received: July 4, 2020; Accepted: October 16, 2020; Published: October 22, 2020
Corresponding author: Yue Teng. Tel: +86-10-66948407; E-mail: yueteng@sklpb.org.
Abstract: As the demand for high-performance computing continues to grow, traditional computing models are facing unprecedented challenges. Among the many emerging computing technologies, DNA computing has attracted much attention due to its low energy consumption and parallelism. The DNA circuit, which is the basis for DNA computing, is an important technology for the regulation and processing of the molecular information. This review highlights the basic principles of DNA computing, summarizes the latest research progress, and concludes with a discussion of the challenges of DNA computing. Such integrated molecular computing systems are expected to be widely used in the fields of aerospace, information security and defense system.
Keywords: DNA circuitDNA computingDNA strand replacement technologygene circuitDNA chip
计算机的发展已经有很长的历史,设计用来便利计算的工具的历史更长。当今社会,电子计算机在我们的日常生活中占有主导地位,没有它的帮助,我们的生活显得举步维艰。然而,随着社会和技术的发展,许多工程中的复杂系统不断涌现,在这些复杂系统的研究领域内,充斥着各种各样的问题。其主要是由于电子计算机的串行计算方式导致存储容量太小,量子物理学已经预测出基于这种形式的芯片的微处理能力不可能长期地保持下去,基于这两点原因及制造技术的局限,探索新的计算方式势在必行。很早以前就有人提出现代计算机的基本部件应该逐步过渡到分子水平[1-3],这样也有利于实现计算机技术的微型化,DNA计算在这种思想和需求下应运而生,在接下来的若干年备受科学界关注。
DNA计算是一种全新的计算模式,也是信息科学与生物科学相结合的一种新兴思维模式[3-4]。其基本思想是利用生物有机分子的信息处理能力来代替数字物理开关元器件,即利用DNA分子的双螺旋结构和碱基互补配对的性质,将所要处理的问题编码为特定的DNA分子链,当输入的DNA分子链与作为开关的特定DNA分子链进行碱基互补配对时,将产生输出DNA分子链,且输出DNA分子链的浓度与输入DNA分子链的浓度呈正比例关系,上述过程构成了一个简单的模拟电路;在生物酶的作用下,或者某些生化操作下,通过合成或者破坏化学键实现加减法、乘法的运算,DNA电路使用特定的DNA链的浓度作为信号;通过各种现代分子生物技术测量反应达到平衡时特定浓度来解决数学问题,并得出运算结果[4-6]。随着合成生物学技术的迅速发展,DNA计算以其并行运算、良好的相容性引起了广泛的研究兴趣。
目前,尽管基于DNA计算的生物电子技术尚处于发展阶段,但通过组装微小的生物元件电路,构建并行生物计算系统的设想却早已成形。1994年Adleman首先提出DNA计算模型的概念,其利用DNA碱基互补配对原则的热力学平衡过程构建了模型,以计算哈密尔顿路径问题,并取得了成功[7]。2004年,Okamoto等3位****首次将数字电路与DNA计算相结合,构建DNA电路,并形成DNA逻辑门,即将不同级逻辑门通过级联的形式组成复杂的电路,最终实现通用的DNA计算[8]。与此同时,DNA计算也对计算机微纳米芯片领域的发展产生了重要的影响[9-11]。DNA结构形成过程中明确的热力学变化和可预测性使其适用于设计具有许多潜在应用的纳米元件。可将DNA结构和功能特性进行集成,整合为仅含DNA元件的具有自主工作能力的计算装置。利用DNA纳米技术构建以生物分子为基本部件的DNA计算电路,为DNA计算和组装技术实现新一代芯片组装提供了理论基础。2009年,IBM公司宣布用DNA和纳米技术开发下一代微处理芯片,开创了DNA计算的新时代。因此,以DNA计算为主体的生物芯片将是未来计算机芯片核心技术的制高点,其国家战略意义不言而喻。
DNA计算的重要性毋庸置疑,学术界和工业界都对其进行了大量的研究[12-16]。本文在此介绍、讨论这一热点课题,并总结DNA计算的主要技术。我们希望本文能够帮助读者从模拟计算和数字计算两个角度了解这项前沿技术及其进展概况。在此基础上,希望通过本文启发更多的创新解决方案,为DNA计算的实现提供助力。
1 DNA计算原理DNA是生物体内的遗传信息载体。DNA的基本构件是核苷酸,其由糖基、磷酸基和含氮碱基组成。DNA中有4种含氮碱基:腺嘌呤(A)、胸腺嘧啶(T)、鸟嘌呤(G) 和胞嘧啶(C)。这些含氮碱基在DNA中按特定顺序排列以编码遗传信息。一个核苷酸的磷酸基与另一个核苷酸的糖基结合并形成共价键,从而形成核苷酸序列,即单链DNA (Single-stranded DNA,ssDNA)。腺嘌呤和胸腺嘧啶(A-T) 之间以及鸟嘌呤和胞嘧啶(G-C) 之间形成氢键,称为碱基互补配对,即Watson-Crick碱基配对[17]。DNA计算的本质就是利用大量的不同核酸分子杂交,产生类似数学计算过程中某种组合的结果,并且根据限制条件得出约束解。由于不同的DNA分子具有不同的编码形式,当大量随机的DNA分子进行杂交后,每个DNA分子的原始信息就会与其他分子所携带的原始信息进行组合,这就是类似于数学中的组合问题。对DNA分子进行一系列连续的生化操作,可用于模拟特定的运算过程[17-18]。
DNA计算的核心问题是将经过编码后的DNA分子链作为输入,对DNA分子进行生物理化操作,主要是在试管内或其他载体上经过一定时间完成受外部条件控制(温度与酸碱度) 的生物化学反应,尤其是通过各种酶的操作,例如合并、分离、加热与退火、扩增、切割、连接、聚合、检测等分子生物学技术。最后对结果DNA分子(即待求问题的解) 进行萃取[19]。DNA电路是实现任何DNA算术和逻辑功能的基本构件,其由数字逻辑电路或模拟电路组成,DNA计算也同样基于此类逻辑门[20-21]。传统意义上的术语“电路”用于表示可以执行特定功能或算法的物理架构。与之类似,DNA电路代表一组可以执行特定功能的DNA链。DNA电路中不使用任何类型的电压和电流。电路信号是DNA链的浓度或DNA链中特定片段的有无。基于跷跷板的电路(Seesaw-based circuits) 使用DNA链浓度作为信号,而局部电路(Localized circuits) 使用DNA链中特定片段的有无作为信号。表 1中列举了传统计算和生物计算间的主要区别。
表 1 传统计算与生物计算的比较Table 1 Difference between traditional computing and biological computing
| Feature | Traditional computing | Biological computing |
| Ability to build cascade circuits | Moderate | High |
| Assembly and set up | Immediate | Prior preparation us must |
| Energy efficiency[22] | Low (109 operations/Joule) | High (2×1019 operations/Joule) |
| Environmental changes | Less impact | High impact |
| External manipulators | Mouse, attached devices | Chemical, heat etc. |
| Heat generation | High | Nil |
| Individual operations | Fast | Slow |
| Main material used | Inorganic such as Silicon | Biological such as DNA |
| Miniaturization | Not efficient at small sizes | Highly efficient at small sizes |
| Process | Deterministic | Stochastic |
| Simultaneous | Fewer | High (Billions) |
| Storage density[23] | Less, limited by technology | High (1 g DNA can store 2.2 PB) |
表选项
2 DNA计算模块DNA链既具有强大的信息存储能力,又可经过电路设计以执行不同的复杂逻辑运算,并且优于现在计算机的并行处理信息的方式,尤其是集成的计算模块拥有超强的计算能力,可解决传统计算机难以处理的难题,因此,DNA计算模块是该领域的研究热点[18-21]。DNA分子经过生物电路设计以执行不同的逻辑运算,而逻辑运算是任何计算模块的基本原则(图 1)。所有的DNA计算控制模块都由3个基本元件构成,第一部分是生物传感器,用于感知生物信息的变化,将其他物理输入转换为可供DNA电路计算设备处理的生化信号;第二部分是控制器,用于调节与生物计算装置相关的信号;第三部分是执行器,用来接收控制器所发出的生化信号并进行相应的电路计算操作[13-16]。DNA计算模块可基于生物分子的逻辑门分为细胞内系统和无细胞系统。也可根据不同底物将其分为基于核酸和基于蛋白质的计算。根据酶的有无,基于核酸的计算可进一步分为有酶和无酶计算[24]。
 |
| 图 1 逻辑门与真值表,分别为与门(A)、或门(B)和非门(C) Fig. 1 The logic symbols and truth tables, including the AND gate (A), the logic OR gate (B) and the logic NOT gate (C). |
| 图选项 |
DNA链置换的概述如图 2所示。单链黏性末端是一个通常含有3–6个碱基对的短DNA片段。图中每个数字代表链中的一个片段。带星号(*)的数字代表该片段的互补链,不同字母代表不同的链。链A是具有单链黏性末端2*的部分双链,由于链B具有片段2 (片段2*的互补链),其可与链A进行反应。与链A结合后,单链黏性末端将链E从链A中置换出来。图 2中链C为中间链,而终产物是链D和链E。DNA链位移的反应速度取决于单链黏性末端片段的长度、链中碱基对的性质和链的浓度。
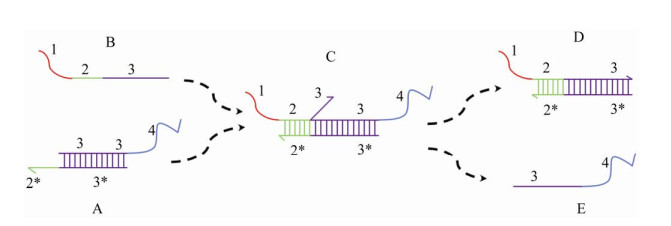 |
| 图 2 DNA置换链过程(A链与B链反应生成C链,反应继续进行,从C链中置换出E链,并产生D链) Fig. 2 The process of DNA strand displacement response. Strand (A) reacts with strand (B) to form strand (C), and the reaction continues, displacing strand (E) from strand (C) and producing strand (D). |
| 图选项 |
DNA链置换技术是DNA计算的一种主要模块,其具有自发性、并行性、可编程性、动态级联性等特点,在DNA计算发展历史上占据重要的地位[19-25]。DNA链置换反应是单链黏性末端介导的分支迁移和链置换反应的简称,也是一种物理实现复杂计算或行为的方法。与酶催化反应相比,无酶体系的反应速度较低且计算耗时较长。自由能驱动的DNA链置换反应受限于反应物初始量,且达到平衡状态的系统无法处理更多的信息[26]。DNA链置换反应的一个重要特性是可级联,一个反应的输出可作为其下游反应的输入。这一特性使DNA链置换反应能够被放大并执行更复杂的运算。尽管寿命有限且耗时较长,DNA链置换反应设计可通过预测核酸杂交和链置换动力学进行控制。实验证实可通过调整单链黏性末端长度和序列组成在106数量级范围内定量控制链置换的反应速率[26-27]。序列设计日益增长的重要性推动了自动化软件的开发,如“DNA链位移”软件[28]。
与DNA链相比较,具有一定生物功能的基因则是设计传感器、计算电路和执行装置/机器的较优候选材料。基因调控是将隐藏在DNA序列中的遗传信息转化为功能蛋白的过程,包括转录和翻译两个步骤[29]。基于生物调控功能的基因线路则是DNA计算的另一种重要模块[30]。基因线路代表一组可以执行特定功能的基因连锁反应。线路信号是基因表达的浓度或特定基因表达的有无。基因线路的输出基因可用作执行装置的触发器。通过信号接收器,实现转录活化激活,产生下游基因表达并输入基因回路。在分子遗传的基本过程中转录发生在先,RNA聚合酶将特定的DNA序列复制到信使RNA (绿线表示促进)。需要注意的是,转录的启动通常需要启动子(同一DNA链的一个特殊区域) 和转录因子(蛋白质)。之后翻译启动,核糖体根据信使RNA产生多肽,多肽折叠形成功能蛋白。基因表达的最终输出信号是蛋白质;输入信号是能够影响基因表达的分子,如阻遏蛋白可抑制转录或翻译(灰线表示抑制),RNA聚合酶和转录因子启动基因表达,诱导因子可通过抑制阻遏蛋白或激活转录因子来促进转录。不同的基因调控可以看作是不同的基因线路构件,以集成为具有复杂逻辑运算能力的基因电路[31-34]。
3 DNA计算的数字逻辑逻辑门是任何数字电路的基本构件。逻辑门中的信号为真(逻辑高或1) 或假(逻辑低或0)。在传统的电子电路中,这些信号由不同的电压水平表示。基本逻辑门有AND、OR、XOR、NOT、NAND、NOR和XNOR[21-24]。其中,NAND和NOR是通用门,即其中任何一者可用来构建任何复杂电路。DNA逻辑门有两种架构:基于扩散的设计和DNA折纸表面的局部设计。
在基于扩散的架构中,DNA链在试管中混合,以链浓度作为信号,并基于阈值分配逻辑高和逻辑低信号。如果一条DNA链的浓度高于特定阈值,则认为该信号为逻辑高,否则为逻辑低。
这种架构中的基本逻辑门是由积分门和放大门组合而成的阈值门。设计中使用的阈值决定了阈值门的数字逻辑操作。这种DNA逻辑门也被称为跷跷板逻辑门,基于跷跷板逻辑门的电路由Qian和Winfree于2011年提出,通过跷跷板门将所有的逻辑门组合在一起[35-37]。设计者可以通过5部分完成DNA电路的设计,这5个部分为给定AND-OR-NOT电路、双轨逻辑(Dual-rail logic)、跷跷板门、DNA结构域和DNA序列。这种DNA逻辑电路缺少NOT操作,故采用双轨逻辑结构。此后,2018年Qian等提出了一种赢者通吃网络,该网络由5部分组成:第一部分为权重乘法,利用DNA链置换反应产生中间产物Pij;第二部分为加权和,通过将第一部分中同一神经元内的中间物种转换为共同的加权和Sj;第三部分为比较加权和,通过“两两湮灭”反应,得到最后的赢者;第四部分为信号恢复反应,使赢者的浓度回到最初设置的浓度,同时产生输出物种;第五部分为将输出物种转换为更易观测的荧光信号[38]。该网络的输入输出为布尔值,但是计算模式为神经网络。但是,基于扩散的电路需要为每个逻辑门提供唯一的DNA链用于门操作,这不利于实现无泄漏的大型复杂数字电路。
与上述DNA链作为信号的传统设计不同,由基因调控过程构建的数字逻辑门,则是用更为接近生物学的方法来建立基因电路。此种方法旨在集成合成基因网络,使其不但能够像目前控制计算机一样轻松编程,而且其逻辑层次与网络规模可逐级扩展。该种方法经过近些年的不断发展,已有多种基础电路和信号处理电路等基因电路构件,主要的细胞构件包括胞内计算组件和胞外通信器件[39]。Nielsen等通过参考FPGA的编码方式进行设计了一个自动化设计基因电路的平台Cello[40]。Cello的运作流程如图 3所示。该平台的编码方式与Verilog相似,因此在设计一个基因电路时,首先选择输入的小分子和输出的蛋白,然后将真值表以Verilog的格式编写,并在平台内运行。之后,平台会根据真值表生成一个数字电子电路,应采用数据库中的生物分子如蛋白小分子构建成生物电路。基因电路突起的箭头为启动子,虚线上的圆圈表示核糖酶绝缘体,半圆是核糖体结合位点,粗箭头表示蛋白编码序列,“T”表示终止子。黑色的箭头表示需要依靠输入的小分子才可激活的启动子,其他颜色的箭头需要对应颜色的编码蛋白序列产生的蛋白去激活。最终的输出采用荧光蛋白来表示,若荧光蛋白的浓度高于阈值则为真,否则为假。DNA链的移动,从而使其能够在电路中重复使用。DNA链的存在与否而不是链浓度在空间定位DNA电路中代表逻辑高或低。文献中已报道多种相关架构,包括基于局部发夹的电路(Localized hairpin-based circuits)、基于化学反应网络(Chemical reaction network,CRN) 和基于分子漫步的电路(Molecular-walker circuits)。在这些架构中,基于局部发夹的电路可以进行AND、OR和多逻辑(Majority logic) 运算,而基于表面CRN和分子漫步的电路可以实现AND、OR和NOT逻辑运算。此外Zadegan等提出一种用于操作所有逻辑门的设计方法,包括AND、OR、XOR及其反操作[41]。此外,用于概念验证的模糊逻辑门系统已在DNA折纸盒中实现。这些基本的布尔DNA逻辑门都具有通用结构,即两类DNA复合物,易于放大。在此研究中,输入信号是DNA链,输出信号则用荧光共振能量转移(Fluorescence resonance energy transfer,FRET) 表示[42]。
 |
| 图 3 Cello的主要过程(根据真值表产生电子电路,最后根据电子电路生成生物电路) Fig. 3 The primary process of Cello. Generating electronic circuit according to the truth table, and finally generating biological circuit according to the electronic circuit. |
| 图选项 |
4 DNA计算的模拟电路DNA电路并不限于数字电路,文献中也报道了多种模拟电路。模拟DNA电路与数字DNA电路的一个显著区别是,模拟DNA电路的输入和输出信号通常用分子浓度来表示,即模拟DNA元件能够感知特定分子在具体环境中的浓度,然后通过适当的模拟计算产生固定浓度的输出信号[43]。如在细胞内部等资源有限的环境中,模拟电路优于数字电路。首先,由于在给定精度范围内,模拟DNA电路中应用于执行数值计算的逻辑门数明显少于数字DNA电路[44],因此,模拟DNA电路可显著节省相关反应所需的各种物质;其次,模拟DNA电路的效率高于数字DNA电路。各种生化反应的本质是模拟计算,细胞因此具有模拟信号而非数字信号的基础[45];再次,数字DNA电路中的“1”和“0”过于简单,不能充分反映信号的影响。
模拟电路中最基础的一个元件为晶体管,但是DNA电路无法转变为DNA晶体管电路,因此在DNA模拟电路中在行为层面上将模拟电子电路映射到模拟DNA电路。此外,放大器和定时器电路也是重要的模拟DNA电路。所有此类电路使用DNA链浓度作为信号。在DNA链置换反应中,DNA模拟电路的输入和输出信号为单链DNA的浓度;双链DNA复合物用于传递信息可以理解为电子电路中的导线。Yordanov等构建了模拟电子电路中最常见的反馈控制电路[46]。Chen等通过比较两种DNA链的浓度,依据DNA链会从浓度低的向浓度高转化,构建了一个基于3种DNA反应的决策器[47]。Song等设计出一些模拟运算如加法、减法和乘法,并利用这些基本运算设计出多项式函数和其他函数[48]。采用DNA链置换反应的模拟电路,可以与不同模拟电路进行连接以完成更加复杂的任务。两个模拟电路进行连接时,需要采用一个额外的模块,将第一个模拟电路的输出信号转为所连接的另一个模拟电路的输入信号,并且不改变信号的唯一性。
基于调控表达的模拟电路可以在活细胞内进行逻辑运算。Sarpeshkar等通过输入两种物质刺激不同的启动子产生相同的蛋白,将蛋白的浓度作为输出结果,从而实现一个加法运算[49]。模拟电路的输出蛋白可以作为另一个电路的输入信号,从而构成基因电路的级联。Daniel等采用级联的方式在活细胞中构建对数域的模拟电路[50]。图 4为函数y=ln(1+x),从图中可以看出输入信号x为AHL诱导因子的浓度,输出信号y为mCherry蛋白质的浓度。输入信号x诱导因子AHL会协助转录因子LuxR和启动子PLux结合,产生蛋白LuxR和绿色荧光蛋白(Green fluorescent protein,GFP)。作为产物的蛋白LuxR也可作为转录因子与启动子结合,因此基因表达(A) 是一个正反馈。基因表达(B) 可以利用基因表达(A) 产生的LuxR蛋白作为转录因子激活启动子PLux,从而产生红色的荧光蛋白mCherry。由A和B组成的模拟电路,其输入AHL的浓度和输出mCherry的浓度对应关系符合函数y=ln(1+x)。Leavitt等已经证明在电子电路中,模拟电路与数字电路相结合后资源利用率达到最高[51]。因此,类比电子电路,我们也可以做出相同的假设,在DNA电路中,模拟电路与数字电路共同作用后可获得最高的资源利用率。而模拟电路与数字电路相结合,需要一种装置完成数字量和模拟量间的转换,而Salehi等提出了关于神经生物学的模数转换和数模转换[44]。
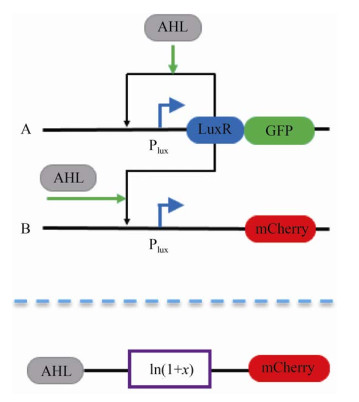 |
| 图 4 生物构建的ln(1+x)的电路(A为正反馈,B为输出表达,虚线下图表示输入AHL和mCherry的对应关系) Fig. 4 Biologically constructed ln(1+x) circuit. A is the positive-feedback, and B is the output expression. The dotted line below shows the corresponding relationship between the input AHL and output mCherry. |
| 图选项 |
5 总结与展望生物学和数学各有其复杂性,但是可以借助数学来研究生物学,同样,也可用生物学来解答数学。由此,生物学和数学这两大主要领域的交叉形成了系统与合成生物学这一跨学科的研究领域[51-53]。DNA计算是系统与合成生物学的一个重要组成部分。DNA计算的基本原理包含两个部分:1) 生物体所具有的复杂结构是由一系列DNA的简单操作而产生的复杂结果;2) 求一个复杂函数f(w) 的值,可通过将复杂函数f(w) 转换为用简单的函数关系求变量w的过程。基于上述原理,当前DNA计算主要研究方向有以下几个方面:1) DNA计算的生物工具;2) DNA计算的集成模块;3) DNA计算的逻辑门;4) DNA智能计算机。DNA计算是一种全新的计算模式,同时,也是生物学与信息学相结合的一种全新的思维模式,通过利用有机分子处理信息的能力来代替数字开关元件这一过程是DNA计算的基本思想[54-57]。相对于传统的电子计算机,DNA电路目前在计算方面存在局限性,其运算时间长且只能进行简单计算,因此不能和电子设备竞争,但相对于传统的硅电路,DNA电路具有体积小、存储量大、能耗低、并行化等优点,而且DNA电路也可在潮湿的环境下运行,有利于将来在细胞内进行部署与计算。
与电子计算机相比,DNA计算机具有以下优点:首先,DNA计算机最大的优点是其并行计算的能力[44, 51]。尽管相对于电子计算而言,DNA计算的每个操作都要花费更多的时间,但DNA计算的真正优势在于它所固有的并行机制,即每步操作并不是依次在单个DNA链上进行的,而是在多个DNA链上同步进行,DNA反应的并行性足以满足当前的计算需求。其次,DNA计算具有较高的能量效率和存储容量[16-17, 57]。电子计算机的能量效率非常低,在操作过程中一部分电能转化为热能而浪费。而用于实现DNA计算操作所用的酶,是在进化过程中产生的,具有很高的能量效率。另外,DNA分子具有非常高的信息存储密度[22]。但是,DNA计算机的障碍主要来自3个方面。其一,对大规模系统进行物理处理时产生的错误。其误差来自多个方面,例如DNA链在传输过程中会物理丢失[26, 28, 30]。其二,DNA计算框架可用生物学和生物技术的聚合酶链式反应(Polymerase chain reaction,PCR) 来实现,但在PCR扩增环节存在基因突变的问题。其三,在利用基于调控表达模式实现模拟电路的过程中存在泄露和非线性问题,模拟电路的输入和输出均为DNA链的浓度或蛋白浓度,但目前在浓度检测过程中缺少快捷高效的检测仪器[30, 40-41]。然而,DNA计算逻辑上对处理多种计算问题具有多用性和有效性[39-40, 42]。对于各种计算问题,将问题转换为DNA计算系统,即DNA生物化学反应的运算途径,以便寻求输出最优解技术路线,使得DNA计算机能够适应广泛的计算问题,并具实用性。尽管证实了DNA计算是通用计算,但是DNA计算在实际应用中无法取代电子计算。其最优方案是利用DNA计算实现高度并行任务,而固有的串行任务仍采用电子计算完成。此外,本文还介绍了DNA计算的数字计算和模拟计算,数字计算与模拟计算最简单的区别在于,数字计算的输出只有0和1这两种表示形式,而模拟计算的输出为一个量值。除此之外,本文还介绍了DNA的两种计算方式即DNA置换反应计算和基于基因表达的计算。这两种计算方式除了反应原理的不同,其输入和输出的物质也不相同,因此我们可以根据其输入和输出物质决定计算的方式。
正是DNA计算有上述优势,使得DNA计算在未来的科学领域中,有望在优化计算、密码学、数学等领域取得突破性的创新和应用。DNA电路设计是一门新兴的交叉学科,尽管现阶段的DNA计算与发展了半个多世纪的电子计算相比,确实显得微不足道。但分子计算的概念却拓宽了人们对自然计算的认识,特别是在生物学中对基本算法的认识。数字革命改变了人类与数据的关系,将社会带入了信息时代。DNA计算有望替代当前主流的计算形式。同时,原本为生命科学应用而开发的DNA合成、测序和检索技术也可被应用于数据存储系统[57]。随着DNA计算研究的不断深入,在未来将出现为DNA计算量身定制的逻辑运算技术,以逐步消除其在应用中遇到的障碍。
参考文献
| [1] | Feynman RP. There's plenty of room at the bottom. Resonance, 2011, 16(9): 890-905. DOI:10.1007/s12045-011-0109-x |
| [2] | Amos M. Theoretical and experimental DNA computation. Bull European Assoc Theor Comput Sci, 1999, 67: 125-138. |
| [3] | Hameed K. DNA computation based approach for enhanced computing power. Int J Emerging Sci, 2011, 1: 23-30. |
| [4] | Kumar SN. A proper approach on DNA based computer. Am J Nanomater, 2015, 3(1): 1-4. |
| [5] | Saxena S. Introduction to DNA computing. Int Acadmey Eng Medical Res, 2016, 1: 1-3. |
| [6] | Khalil AS, Collins JJ. Synthetic biology: applications come of age. Nat Rev Genet, 2010, 11(5): 367-379. DOI:10.1038/nrg2775 |
| [7] | Adleman LM. Molecular computation of solutions to combinatorial problems. Science, 1994, 266(5187): 1021-1024. DOI:10.1126/science.7973651 |
| [8] | Okamoto A, Tanaka K, Saito I. DNA logic gates. J Am Chem Soc, 2004, 126(30): 9458-9463. DOI:10.1021/ja047628k |
| [9] | Yin J, Wang JK, Niu RJ, et al. DNA Nanotechnology-based biocomputing. Chem Res Chin Univ, 2020, 36(2): 219-226. DOI:10.1007/s40242-020-9086-5 |
| [10] | Li J, Green AA, Yan H, et al. Engineering nucleic acid structures for programmable molecular circuitry and intracellular biocomputation. Nat Chem, 2017, 9(11): 1056-1067. DOI:10.1038/nchem.2852 |
| [11] | Seo J, Kim S, Park HH, et al. Nano-bio-computing lipid nanotablet. Sci Adv, 2019, 5(2): eaau2124. DOI:10.1126/sciadv.aau2124 |
| [12] | Wiraja C, Zhu Y, Lio DCS, et al. Framework nucleic acids as programmable carrier for transdermal drug delivery. Nat Commun, 2019, 10: 1147. DOI:10.1038/s41467-019-09029-9 |
| [13] | Fu T, Lyu YF, Liu H, et al. DNA-based dynamic reaction networks. Trends Biochem Sci, 2018, 43(7): 547-560. DOI:10.1016/j.tibs.2018.04.010 |
| [14] | Pugh GC, Burns JR, Howorka S. Comparing proteins and nucleic acids for next-generation biomolecular engineering. Nat Rev Chem, 2018, 2(7): 113-130. DOI:10.1038/s41570-018-0015-9 |
| [15] | Su YW, Li D, Liu BY, et al. Rational design of framework nucleic acids for bioanalytical applications. Chem Plus Chem, 2019, 84(5): 512-523. |
| [16] | Zhang C, Ge LL, Zhuang YC, et al. DNA computing for combinational logic. Sci China Inf Sci, 2018, 62(6): 61301. |
| [17] | George AK, Kunnummal IO, Alazzawi L, et al. Design of DNA digital circuits. IEEE Potent, 2020, 39(2): 35-40. DOI:10.1109/MPOT.2018.2859443 |
| [18] | Marchisio MA. Parts & pools: a framework for modular design of synthetic gene circuits. Front Bioeng Biotechnol, 2014, 2: 42. |
| [19] | George AK, Singh H. Enzyme-free scalable DNA digital design techniques: a review. IEEE Trans Nanobiosci, 2016, 15(8): 928-938. DOI:10.1109/TNB.2016.2623218 |
| [20] | Green AA, Kim J, Ma D, et al. Complex cellular logic computation using ribocomputing devices. Nature, 2017, 548(7665): 117-121. DOI:10.1038/nature23271 |
| [21] | Siuti P, Yazbek J, Lu TK. Synthetic circuits integrating logic and memory in living cells. Nat Biotechnol, 2013, 31(5): 448-452. DOI:10.1038/nbt.2510 |
| [22] | Kari L. DNA computing: arrival of biological mathematics. Math Intell, 1997, 19(2): 9-22. DOI:10.1007/BF03024425 |
| [23] | Yazdi SMHT, Yuan YB, Ma J, et al. A rewritable, random-access DNA-based storage system. Sci Rep, 2015, 5: 14138. DOI:10.1038/srep14138 |
| [24] | Miyamoto T, Razavi S, DeRose R, et al. Synthesizing biomolecule-based Boolean logic gates. ACS Synth Biol, 2013, 2(2): 72-82. DOI:10.1021/sb3001112 |
| [25] | Wang F, Lv H, Li Q, et al. Implementing digital computing with DNA-based switching circuits. Nat Commun, 2020, 11: 121. DOI:10.1038/s41467-019-13980-y |
| [26] | Zhang DY, Seelig G. Dynamic DNA nanotechnology using strand-displacement reactions. Nat Chem, 2011, 3(2): 103-113. DOI:10.1038/nchem.957 |
| [27] | Zhang DY, Winfree E. Control of DNA strand displacement kinetics using toehold exchange. J Am Chem Soc, 2009, 131(47): 17303-17314. DOI:10.1021/ja906987s |
| [28] | Phillips A, Cardelli L. A programming language for composable DNA circuits. J Roy Soc Interface, 2009, 6 Suppl 4(47): S419-S436. |
| [29] | Crick F. Central dogma of molecular biology. Nature, 1970, 227(5258): 561-563. DOI:10.1038/227561a0 |
| [30] | Brophy JAN, Voigt CA. Principles of genetic circuit design. Nat Methods, 2014, 11(5): 508-520. DOI:10.1038/nmeth.2926 |
| [31] | Weinberg BH, Pham NTH, Caraballo LD, et al. Large-scale design of robust genetic circuits with multiple inputs and outputs for mammalian cells. Nat Biotechnol, 2017, 35(5): 453-462. DOI:10.1038/nbt.3805 |
| [32] | Bradley RW, Buck M, Wang BJ. Tools and principles for microbial gene circuit engineering. J Mol Biol, 2016, 428(5): 862-888. DOI:10.1016/j.jmb.2015.10.004 |
| [33] | Kitada T, DiAndreth B, Teague B, et al. Programming gene and engineered-cell therapies with synthetic biology. Science, 2018, 359(6376): eaad1067. DOI:10.1126/science.aad1067 |
| [34] | Je Lee Y, Hoynes-O'Connor A, Leong MC, et al. Programmable control of bacterial gene expression with the combined CRISPR and antisense RNA system. Nucleic Acids Res, 2016, 44(5): 2462-2473. DOI:10.1093/nar/gkw056 |
| [35] | Qian LL, Winfree E. Scaling up digital circuit computation with DNA strand displacement cascades. Science, 2011, 332(6034): 1196-1201. DOI:10.1126/science.1200520 |
| [36] | Qian LL, Winfree E. A simple DNA gate motif for synthesizing large-scale circuits. J Roy Soc Interface, 2011, 8(62): 1281-1297. DOI:10.1098/rsif.2010.0729 |
| [37] | Qian LL, Winfree E, Bruck J. Neural network computation with DNA strand displacement cascades. Nature, 2011, 475(7356): 368-372. DOI:10.1038/nature10262 |
| [38] | Cherry KM, Qian LL. Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks. Nature, 2018, 559(7714): 370-376. DOI:10.1038/s41586-018-0289-6 |
| [39] | Weiss R, Basu S, Hooshangi S, et al. Genetic circuit building blocks for cellular computation, communications, and signal processing. Nat Comput, 2003, 2(1): 47-84. DOI:10.1023/A:1023307812034 |
| [40] | Nielsen AAK, Der BS, Shin J, et al. Genetic circuit design automation. Science, 2016, 352(6281): aac7341. DOI:10.1126/science.aac7341 |
| [41] | Zadegan RM, Jepsen MDE, Hildebrandt LL, et al. Construction of a fuzzy and Boolean logic gates based on DNA. Small, 2015, 11(15): 1811-1817. DOI:10.1002/smll.201402755 |
| [42] | George AK, Singh H. Design of computing circuits using spatially localized DNA majority logic gates//2017 IEEE International Conference on Rebooting Computing (ICRC). Washington, DC, USA: IEEE, 2017: 1-7. |
| [43] | Benenson Y, Gil B, Ben-Dor U, et al. An autonomous molecular computer for logical control of gene expression. Nature, 2004, 429(6990): 423-429. DOI:10.1038/nature02551 |
| [44] | Sarpeshkar R. Analog versus digital: extrapolating from electronics to neurobiology. Neural Comput, 1998, 10(7): 1601-1638. DOI:10.1162/089976698300017052 |
| [45] | Sauro HM, Kim K. It's an analog world. Nature, 2013, 497(7451): 572-573. DOI:10.1038/nature12246 |
| [46] | Yordanov B, Kim J, Petersen RL, et al. Computational design of nucleic acid feedback control circuits. Acs Synth Biol, 2014, 3(8): 600-616. DOI:10.1021/sb400169s |
| [47] | Chen YJ, Dalchau N, Srinivas N, et al. Programmable chemical controllers made from DNA. Nat Nanotechnol, 2013, 8(10): 755-762. DOI:10.1038/nnano.2013.189 |
| [48] | Song TQ, Garg S, Mokhtar R, et al. Analog computation by DNA strand displacement circuits. ACS Synth Biol, 2016, 5(8): 898-912. DOI:10.1021/acssynbio.6b00144 |
| [49] | Sarpeshkar R. Analog synthetic biology. Philos Trans Roy Soc A Math Phys Eng Sci, 2014, 372(2012): 20130110. |
| [50] | Daniel R, Rubens JR, Sarpeshkar R, et al. Synthetic analog computation in living cells. Nature, 2013, 497(7451): 619-623. DOI:10.1038/nature12148 |
| [51] | Friedland AE, Lu TK, Wang X, et al. Synthetic gene networks that count. Science, 2009, 324(5931): 1199-1202. DOI:10.1126/science.1172005 |
| [52] | Rubens JR, Selvaggio G, Lu TK. Synthetic mixed-signal computation in living cells. Nat Commun, 2016, 7: 11658. DOI:10.1038/ncomms11658 |
| [53] | Tamsir A, Tabor JJ, Voigt CA. Robust multicellular computing using genetically encoded NOR gates and chemical 'wires'. Nature, 2011, 469(7329): 212-215. DOI:10.1038/nature09565 |
| [54] | Anderson JC, Voigt CA, Arkin AP. Environmental signal integration by a modular AND gate. Mol Syst Biol, 2007, 3(1): 133. DOI:10.1038/msb4100173 |
| [55] | Roquet NB, Lu TK. Digital and analog gene circuits for biotechnology. Biotechnol J, 2014, 9(5): 597-608. DOI:10.1002/biot.201300258 |
| [56] | Purcell O, Lu TK. Synthetic analog and digital circuits for cellular computation and memory. Curr Opin Biotech, 2014, 29: 146-155. DOI:10.1016/j.copbio.2014.04.009 |
| [57] | Song X, Reif J. Nucleic acid databases and molecular-scale computing. ACS Nano, 2019, 13(6): 6256-6268. DOI:10.1021/acsnano.9b02562 |
