<script type="text/javascript" src="https://cdn.bootcss.com/mathjax/2.7.2-beta.0/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script> <script type='text/x-mathjax-config'> MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]}});</script> 郎艺超, 肖璐, George Christakos
浙江大学海岛与海岸带研究所, 舟山 316021
收稿日期: 2017-04-07; 修回日期: 2017-08-10; 录用日期: 2017-08-29
基金项目: 国家自然科学基金（No.41671399）
作者简介: 郎艺超(1994-), 男, E-mail:langyichao1@sina.com
通讯作者（责任作者）: George Christakos(1956—), 浙江大学海岛与海岸带研究所教授, 外专千人, 研究方向为时空地统计学, E-mail:gchristakos@zju.edu.cn

摘要: 基于SARIMA模型对杭州市主城区内的7个站点和周边3个站点的PM_2.5浓度进行4 h平均的短期预报，并利用普通Kriging法对杭州市主城区PM_2.5进行空间插值和制图.在建立SARIMA模型时，用批量自动化的方法，使用R语言编程对夏季和冬季各360期的数据进行SARIMA（p，d，q）×（P，D，Q）₆模型的参数的确定和拟合，来预测下一期的值.在10个站点分别进行120期的预测，做出真实与预测的时间序列图，在精度分析中，夏季和冬季PM_2.5浓度总体的平均绝对误差（MAE）分别为8.4 μg·m^-3和14.8 μg·m^-3.在ArcGIS中，对每期的数据使用普通Kriging法，用球面模型拟合半变异函数，决定各个站点的权重，来对杭州市区内未知空间样点进行插值，最后生成完整的杭州市主城区PM_2.5短期预测图.本研究创新性地将SARIMA模型广义化运用到小尺度时间序列中，预报效果较好，并且批量自动化预测和制图的方法，可为今后的预测制图产品化提供技术支持.
关键词:SARIMA模型PM_2.5普通Kriging法杭州市预测制图
Forecasting concentrations of PM_2.5 in main urban area of Hangzhou and mapping using SARIMA model and ordinary Kringing method
LANG Yichao, XIAO Lu, George Christakos
Institute of Islands and Coastal Ecosystems, Zhejiang University, Zhoushan 316021
Received 7 April 2017; received in revised from 10 August 2017; accepted 29 August 2017
Supported by the National Natural Science Foundation of China(No.41671399)
Biography: LANG Yichao (1994—), male, E-mail:langyichao1@sina.com
^*Corresponding author: George Christakos, E-mail:gchristakos@zju.edu.cn
Abstract: The average four-hour short-time forecasting of PM_2.5 concentrations of 7 stations in main urban area of Hangzhou and the surrounding 3 stations based on the SARIMA model, and the ordinary Kriging method was used to interpolate and mapping. When establishing the SARIMA model, we use the batch automation method by R language to fit the parameters of the SARIMA(p, d, q)×(P, D, Q)₆ model during respective 360 periods in summer and winter to predict the next value. The PM_2.5 concentrations of 120 periods in each 10 stations were forecasted and then were made into time series charts of the true and predictive value. In precision analysis, the MAE was 8.4 μg·m^-3 and 14.8 μg·m^-3 in summer and winter respectively. In ArcGIS, the ordinary Kriging method was used for interpolating each period of data by means of spherical model to fit semivariogram and determine the weight of each station for interpolating unknown space in Hangzhou. Finally, the short-term PM_2.5 concentrations forecasting maps in main urban area of Hangzhou were completed. This research innovatively generalized the SARIMA model into small scale time series with good prediction precision, and the batch automation method could potentially be employed in the operational forecasting and mapping.
Key words: SARIMA modelPM_2.5ordinary Kriging methodHangzhouforecastmapping
1 引言(Introduction)随着城市化进程的加快, 出现了越来越多的环境污染问题.而雾霾天气不仅损坏了美丽的城市形象, 同时对人们的出行甚至健康产生了巨大的影响, 如导致呼吸道疾病发病率近年来持续增加.PM_2.5是雾霾的主要组成部分, 它是环境空气中空气动力学当量直径≤2.5 μm的颗粒物的总称.PM_2.5的来源包括化石燃料和树木的燃烧, 以及汽车尾气和工厂废气的排放等(吴兑, 2012).为了有效控制PM_2.5, 并提醒市民在PM_2.5浓度升高时减少出行, 对PM_2.5做出有效的预测是非常有必要的.
由于PM_2.5的来源较多, 且这些来源之间存在复杂的关系, 因此, 很难建立它们之间的关系模型.目前的研究中, 模型主要是建立环境因子与PM_2.5之间的复杂关系(马天成等, 2014；刘小生等, 2013；龚明等, 2016；谢永华等, 2015；王黎明等, 2017).Box和Jenkins于20世纪70年代提出了一整套关于时间序列预测方法—自回归积分滑动平均模型(ARIMA), 由于时间序列常常具有季节的周期性变化, 随后他们又在该模型上增加了季节因素, 变为季节乘积自回归积分滑动平均模型(SARIMA).目前, 该模型在流行病学、管理学、社会学中有着广泛的应用(郭丹等, 2016；李瑞法等, 2016；梁文娟等, 2016；陶长余等, 2016；杨仁东等, 2016).SARIMA模型也曾在国外的PM_2.5预测研究中被使用过(Wang et al., 2009), 但该研究使用的季节因素是狭义的, 即大时间尺度的季节因素.笔者通过对PM_2.5浓度的时间序列研究发现, PM_2.5浓度在每天呈周期性变化, 即为广义的季节因素, 因此, 本研究根据PM_2.5随时间变化具有周期自相关性的特点, 创新性地把SARIMA模型广义化, 把每一天看成一年, 每天内的变化看成是季节变化, 建立PM_2.5浓度的小时间尺度的SARIMA模型.选择夏季和冬季这两个具有代表性的季节, 将1 d 24 h逐时的PM_2.5浓度数据分成6份, 以4 h平均PM_2.5浓度作为1期, 这样既能减小由于数据缺失或异常带来的噪音, 又能保证PM_2.5浓度的周期性.使用该模型对杭州市主城区内7个站点及周边的3个站点进行4 h平均PM_2.5浓度的短期预测.最后使用普通Kriging法, 采用球面模型拟合半变异函数, 对杭州市主城区PM_2.5进行空间插值和制图.
2 数据和方法(Data and methods)2.1 研究区域和数据杭州市位于钱塘江的下游, 京杭大运河南端, 由于拥有美丽的西湖及曾经是南宋古都, 使得杭州成为中国南方著名的旅游城市, 因此, 环境问题对杭州显得尤为重要.杭州市包括9个市辖区、2个县, 并代管2个县级市.本文主要研究区域(图 1)为杭州市主城区, 即上城区、下城区、西湖区、拱墅区、江干区, 主城区市中心地理坐标为120°12′E, 30°16′N, 面积约610 km², 人口约330万人.
图 1(Fig. 1)

图 1 杭州市主城区地图及10个检测站点 Fig. 1Map of main urban area in Hangzhou and locations of 10 monitoring sites

本文的PM_2.5浓度数据来自中国环境监测总站(http://www.cnemc.cn), 为了使结论具有普遍性, 选择夏季和冬季两个季节的样本数据, 具体时间范围为2016年5月1日—7月19日(夏季)和2016年11月1日—2017年1月19日(冬季).为了使制图结果更加准确, 防止出现空间插值的边缘效应, 本文在主城区周围增加选择站点, 采用杭州市主城区内的7个检测站点(西溪、下沙、卧龙桥、农大、朝晖五区、和睦小学、云栖)及3个周边站点(滨江、临平镇、城厢镇)的每小时PM_2.5数据, 具体监测站点位置见图 1.为了使数据更具有周期性并能更好地预测PM_2.5的短期浓度, 以及消除在某一时刻由于设备故障或人为原因造成的数据丢失或异常, 把逐时数据以4 h平均浓度作为1期, 1天6期, 共480期, 对数据进行整理.经过上述处理后的数据, 仍出现14处缺失, 但由于缺失的数据量较少, 使用前后期浓度平均值进行缺失值插补.在夏季和冬季样本中, 取前360期(60 d)的数据来建立模型(360期数据随着建模过程不断发生变化), 后120期(20 d)的数据进行验证模型.
2.2 研究方法使用SARIMA模型和普通Kriging法对杭州市主城区PM_2.5浓度进行短期预测和制图, 即先使用SARIMA模型对PM_2.5浓度进行短期预测, 再使用预测得到的数值进行制图, 这两个阶段分别在R编程语言和ArcGIS环境条件下操作, 均使用编程批量化的方法.具体步骤如下：①获取PM_2.5浓度逐小时的观测数据, 以4 h为平均, 处理数据生成时间序列数据, 并分站点建立相应的样本数据库；②将数据分为训练数据和验证数据, 使用训练数据建立SARIMA(p, d, q)×(P, D, Q)_s模型, 使用数据的特征确定参数s、d、D, 再通过建立不同阶数p、q、P、Q的模型, 取AIC最小的方法确定最终模型, 带入数据来预测下一期的值；③用新的一期数据更新训练数据, 重复第2个过程, 直到所有期数和站点都预测完毕；④对得到的预测数据按时间顺序建立预测数据库, 使用普通Kriging法对每期的预测数据进行空间插值和制图.本研究建模与制图流程见图 2.
图 2(Fig. 2)

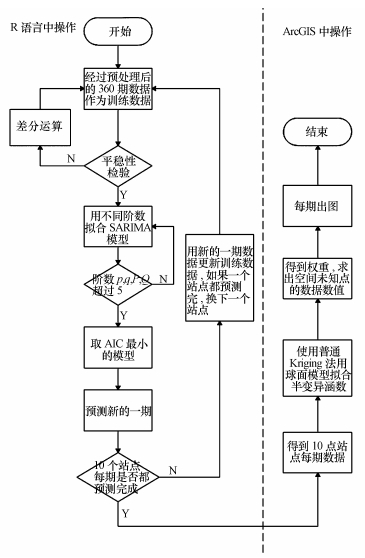图 2 建模与制图的流程图 Fig. 2Flow chart of modeling and mapping

3 预测和制图模型的建立(Development of forecast and mapping model)3.1 SARIMA(p, d, q)×(P, D, Q)_s模型SARIMA模型是在ARIMA模型中增加了季节项, 而ARIMA模型是基于ARMA模型建立的, ARMA模型又叫自回归滑动平均(Auto Regression Moving Average)模型, 简记为ARMA(p, q)模型.它是AR(p)模型(p阶自回归模型)和MA(q)模型(q阶自回归模型)的结合, 即假设对于一个时间序列不仅与它以前时刻对应的值相关, 而且还与以前时刻对应的扰动存在一定的关系, 具体表达式为：

(1)

式中, p为AR模型的阶数, q为MA模型的阶数, x_i为i期属性值, φ_i为t-i期的属性值系数, ε_i为i期的扰动项, θ_i为t-i期扰动项的系数.对于扰动项ε_i, 满足E(ε_i=0, Var(ε_i=σ², 且对于任意的s≠t, E(ε_s, ε_i)=0.在给定最高阶数p、q的情况下, 基于训练数据使用最小二乘法求解回归系数, 但在使用ARMA(p, q)模型前, 首先必须保证拟合模型(或称时间序列)是平稳的, 当时间序列不平稳时, 可考虑对时间序列进行差分, 直到平稳为止, 差分后得到时间序列再进行ARMA模型拟合, 这样的模型称为ARIMA(p, d, q)模型, 具体表述为：

(2)

式中, φ(L)为自回归系数多项式, Θ(L)为移动平均多项式, B为后移算子, ▽^d=(1-L)^d, 表示进行d阶差分运算.
SARIMA模型又称为季节性自回归滑动平均(Seasonal Auto Regression Moving Average)模型, 简记为SARIMA(p, d, q)×(P, D, Q)_s模型, 是在基础的ARIMA模型上增加了季节的因素.同一般的ARIMA模型一样, 季节的周期性因素也可以拟合一个ARIMA模型, 即先对季节性因素进行D阶差分, 再类比用差分后周期为s的季节时间序列建立一般的ARIMA模型, 综合的形式为：

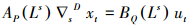(3)

式中, A_P(L^s)为P阶季节自回归算子, B_Q(L^s)为Q阶季节移动平均算子, ▽_s^D表示季节的差分运算, u_t为移除季节因素的时间序列.把一般的ARIMA模型(式(2)), 带入式(3)中的u_t, 即可得到完整的SARIMA(p, d, q)×(P, D, Q)_s模型, 形式为：

(4)

3.2 SARIMA模型参数的选择和预测SARIMA(p, d, q)×(P, D, Q)_s模型共有p、d、q、P、D、Q、s 7个参数.参数s为季节性周期数, 主要由数据的周期性所决定, 模型中d、D参数为模型的差分阶数.首先在SARIMA模型中, MA部分一定是平稳的, ARMA模型的平稳性完全由AR部分的平稳性决定, 为了减少运算时间, 先拟合一个AR(p)模型, 当模型平稳时, AR(p)模型的p个特征根都在单位圆内, 这种方法简称为ADF检验, 即通过拟合系数得到统计量DF, 进行t检验, 当p < 0.05时, 可认为时间序列是平稳的, 当时间序列不平稳时, 可考虑对季节时间序列进行d次时间序列差分, 再进行D次季节时间序列差分, 直到平稳为止, d、D即为模型的差分阶数(Kumar et al., 2010).
在之前的研究中(Wang et al., 2009), 参数p、q、P、Q值都是通过时间序列自相关系数(ACF)和偏相关系数(PACF)的值决定的, 即通过画出ACF和PACF图, 通过目视辨别自相关系数和偏相关系数的截尾性来确定阶数p、q、P、Q的值.但这种方法太过主观, 这里引入一个评价标准, Akaike(1987)提出的赤池信息准则(AIC), 它被定义为拟合精度和参数个数的加权函数：

(5)

式中, k为模型中未知参数的个数, 为模型的极大似然函数值.利用d阶差分好训练数据拟合不同参数p、q、P、Q(p, q, P, Q < 6)的SARIMA模型, 比较各个模型的AIC, 取最小AIC的模型对应的p、q、P、Q值, 即为最终模型的参数.
根据得到参数后的SARIMA(p, d, q)×(P, D, Q)_s模型, 带入训练数据, 使用最小二乘法求解回归系数.在每个建立完成的模型中, 带入已知的数据, 对下一期进行预测.
3.3 普通Kriging法和制图Kriging法是由法国地质统计学家Matheron提出的, 以纪念南非矿业工程师Krige在1951年首次将统计学技术运用到地矿评估中, 其中的普通Kriging法目前已被广泛运用于空间插值中(苏姝等, 2004；弓小平等, 2008；乔改瑞等, 2016).Kriging法用半变异函数模型代表空间中随距离变化的函数, 函数参数的确定方法是用已知的空间数据计算半变异值.本文使用球面模型拟合半变异函数, 在无偏估计与最小估计变异数的条件下, 决定各采样点的权重系数, 最后再以各采样点求得的权重线性组合, 来求空间未知地点(分辨率为0.001°)的估计值.
4 预测效果实例分析(Development of forecast and mapping model)4.1 数据的处理和描述本研究选取杭州市夏季和冬季两个具有代表性的季节进行研究, 分别获取2016年5月1日—7月19日和2016年11月1日—2017年1月19日的逐小时PM_2.5浓度数据.数据站点包括杭州市主城区的7个站点, 以及主城区周边的3个站点, 以减少空间插值制图的边缘效应, 增加制图的准确性.把逐小时的PM_2.5数据以4 h的时间跨度进行平均, 把1天分为6期, 以减少由于人为或是设备故障所引起的数据缺失或者异常情况, 使数据更加稳定.同时, 由于PM_2.5浓度呈现白天较低晚上较高的现象, 将1天分为6期可以获得时间序列的周期性, 以适用于SARIMA模型的建立.
对10个站点PM_2.5浓度的所有数据进行统计, 结果见表 1.从表中可以看出, 在夏季, 朝晖五区站点的PM_2.5浓度相对较高, 为43.6 μg·m^-3, 云溪站点的PM_2.5浓度相对较低, 为28.1 μg·m^-3, 而所有站点在后120期PM_2.5浓度都有减少的趋势；从标准差可以看出, 临平镇站点的PM_2.5波动较大, 但在后120期波动变小.相比于夏季, 冬季各个站点的PM_2.5浓度明显较高, 浓度最高站点朝晖五区可达到74.3 μg·m^-3, 而较低的云溪站点也到达了45.8 μg·m^-3.同时, 从表中还可以得出, 在后120期验证样本中, PM_2.5浓度夏季呈降低的趋势, 而冬季呈升高的趋势.图 3为10个站点夏季和冬季的时间序列图, 其中, 虚线后为120期验证数据的时间序列图.从图 3可以更加直观地看出PM_2.5浓度随着时间变化的定性趋势及每天的周期性.
表 1(Table 1)

表 1 10个站点PM2.5浓度的平均值与标准差 Table 1 Mean and stand error of PM2.5 concentration in 10 sites

表 1 10个站点PM2.5浓度的平均值与标准差 Table 1 Mean and stand error of PM2.5 concentration in 10 sites μg·m-3 站点 夏季PM2.5浓度 冬季PM2.5浓度 总480期 后120期 总480期 后120期 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 滨江 41.0 24.7 31.2 21.0 68.9 41.9 81.0 53.1 西溪 33.6 18.9 23.1 13.8 50.1 30.8 61.1 38.0 下沙 39.1 21.9 30.2 13.7 68.8 43.0 81.4 52.0 卧龙桥 33.4 19.8 23.4 13.6 63.7 40.8 76.6 51.5 农大 34.3 19.1 24.3 14.1 60.5 35.6 72.9 46.6 朝晖五区 43.6 25.4 30.4 17.2 74.3 45.7 88.4 57.7 和睦小学 40.6 23.2 27.5 13.2 67.2 41.3 79.9 53.4 临平镇 42.2 27.2 26.6 13.6 69.3 45.9 78.0 56.4 城厢镇 38.8 21.7 27.8 16.0 60.8 37.0 68.4 44.1 云溪 28.1 16.1 19.6 12.8 45.8 30.6 50.1 34.2

图 3(Fig. 3)

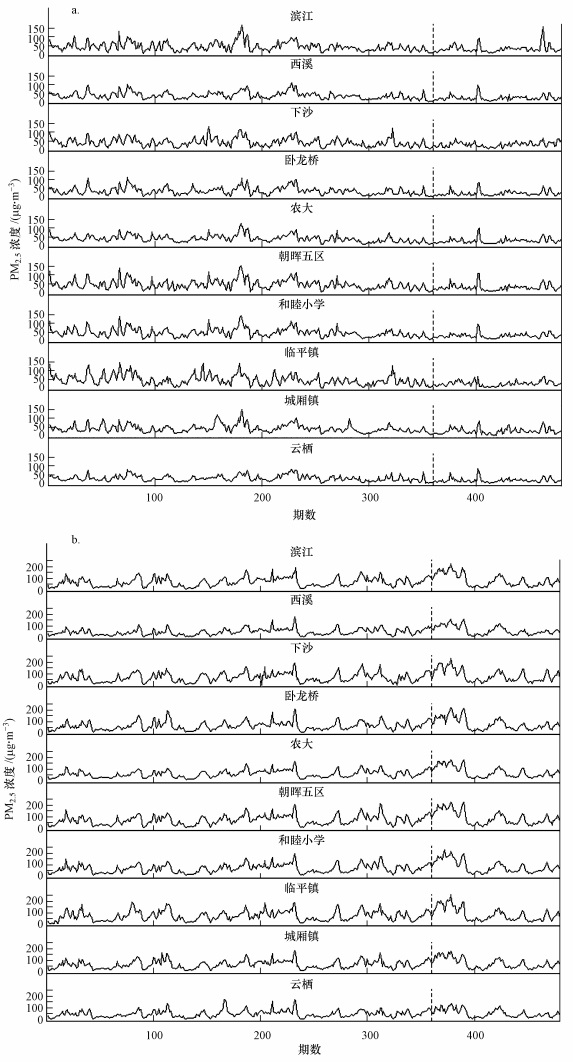图 3 夏季(a)和冬季(b)各站点PM2.5的时间序列图 Fig. 3Time-series plot of all sites in summer (a) and winter(b)

4.2 SARIMA模型建立和预测按照之前所述研究方法, 对于夏季和冬季10个站点的数据分别进行建模预测.在每个季节每个站点中, 使用360期(60 d)数据建立模型, 在模型的参数取值上, 因为将每天分为6期, 所以时间序列的广义季节性周期为6, 即参数s为6.而对于参数p、d、q、P、D、Q的确定, 则按照2.2节所叙述的方法, 针对特定预测的某一期, 取其前360期作为训练数据, 首先对数据进行d阶或季节D阶差分, 使数据平稳；然后使用不同参数p、q、P、Q(p、q、P、Q＜6)的SARIMA模型, 再利用赤池信息准则(AIC), 比较各个模型的AIC, 通过训练数据得到最小AIC所对应的参数p、q、P、Q, 即为最佳参数.因为每期的训练样本不同, 所以每期得到的参数也不尽相同.例如, 在预测滨江站点夏季第10期时, 需要对时间序列进行1阶差分, 使序列稳定, 在比较不同的参数模型后, 发现模型SARIMA(1, 1, 2)×(0, 0, 6)₆的AIC最小, 为3965, 确定该模型为最终模型.在该模型中季节性的MA部分为1阶, 也就是与前一天此时间段的扰动项有关, 非季节性的AR部分为1阶, 说明预测值与前一期的PM_2.5浓度有关, 而MA部分为2阶, 说明预测值与前两期的扰动项有关.模型建立后, 带入数据进行拟合, 得到预测值.为了使模型的预测更有实际意义, 在每个季节, 每一次预测后, 就用真实数据更新一期, 但仍然使用共360期的数据作为训练数据进行训练, 重新确定参数及模型的拟合效果.这样不断重复这个过程, 直到每季所有的120期都预测完成.
4.3 预测结果与评估经过上述流程, 在夏季和冬季中分别建立不同参数的10×120个SARIMA(p, d, q)×(P, D, Q)₆模型, 逐个预测得到10个站点120期PM_2.5的预测值及75%置信区间(Peiris et al., 1988).图 4为夏季、冬季结合真实数据和预测数据的时间序列图, 同时给出了75%置信区间.同时对预测结果进行评估, 评估方法可以比较真实数值和预测数值的接近程度, 本文采用平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分误差(MAPE)等指标来评判(Kumar et al., 2010).具体定义如下：

(6)

(7)

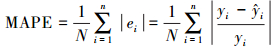(8)

图 4(Fig. 4)

图 4 夏季(a)和冬季(b)PM2.5浓度预测值和真实值的时间序列图(绿色实线为真实值, 红色实线为预测值, 红色虚线为75%置信区间) Fig. 4True and prediction time-series plots in summer(a) and winter(b)(green solid lines are trues, red solid lines are prediction, red dash lines are 75% confidence interval)

式中, y_i为真实值, 为预测值.对10个站点及总体分别计算MAE、MAPE、RMSE值, 具体结果见表 2.
表 2(Table 2)

表 2 10个站点和总体PM2.5浓度的MAE、RMSE、MAPE Table 2 MAE, RMSE, MAPE of PM2.5 concentration in 10 sites and overall

表 2 10个站点和总体PM2.5浓度的MAE、RMSE、MAPE Table 2 MAE, RMSE, MAPE of PM2.5 concentration in 10 sites and overall 站点 PM2.5(夏季) PM2.5冬季 MAE/(μg·m-3) RMSE/(μg·m-3) MAPE MAE/(μg·m-3) RMSE/(μg·m-3) MAPE 滨江 8.0 10.9 0.30 13.4 16.7 0.24 西溪 10.4 16.5 0.40 20.2 26.2 0.27 下沙 6.7 9.1 0.24 10.8 14.4 0.21 卧龙桥 7.8 11.2 0.32 16.7 22.3 0.25 农大 7.0 9.1 0.24 13.1 17.1 0.31 朝晖五区 8.5 12.8 0.45 21.3 30.1 0.25 和睦小学 8.9 12.2 0.35 11.8 14.6 0.28 临平镇 9.1 12.4 0.50 16.5 21.1 0.29 城厢镇 6.2 8.4 0.37 9.7 12.6 0.34 云溪 7.5 13.1 0.46 14.7 20.1 0.32 总体 8.0 11.6 0.36 14.8 19.5 0.27

在夏季, 10个站点PM_2.5浓度的MAE值在6.2~10.4 μg·m^-3之间, RMSE在8.4~16.5 μg·m^-3之间, MAPE在0.24~0.50之间, 总体平均的MAE、RMSE、MAPE分别为8.0 μg·m^-3、11.6 μg·m^-3、0.36.而在冬季, 10个站点PM_2.5浓度的MAE值在9.7~20.2 μg·m^-3之间, RMSE在12.6~30.1 μg·m^-3之间, MAPE在0.21~0.34之间, 总体平均的MAE、RMSE、MAPE分别为14.8 μg·m^-3、19.5 μg·m^-3、0.27.说明在夏季和冬季, 用该方法预测结果均较好, 同时从预测的时间序列图与真实的时间序列图也可以定性的看出, 预测值和真实值比较吻合, 而且基本上所有的真实值都落在了75%置信区间内.但波动较大的地方吻合程度不好, 原因可能是影响PM_2.5浓度变化的外界极端因素增加, 导致的剧烈变化难以预测.
4.4 普通Kriging法的拟合与制图在夏季和冬季, 使用得到的10个站点120期数据, 对每一期数据分别采用普通Kriging法中半变异函数球面模型进行拟合, 得到球面模型参数, 对杭州市主城区范围内的每个未知地点, 根据球面模型的参数得到采样点的权重系数, 线性组合得到完整的预测图.在夏季和冬季, 每季共得到120张不同时间段的预测图, 在240张预测图中(图 5), 选择了夏季和冬季中三分位数的期作为演示, 即夏季第40期(2016年7月6日8:00—11:00)、80期(2016年7月13日0:00—3:00)和冬季第40期(2017年1月6日8:00—11:00)、80期(2017年1月13日0:00—3:00)的PM_2.5浓度预测图(图 5).
图 5(Fig. 5)

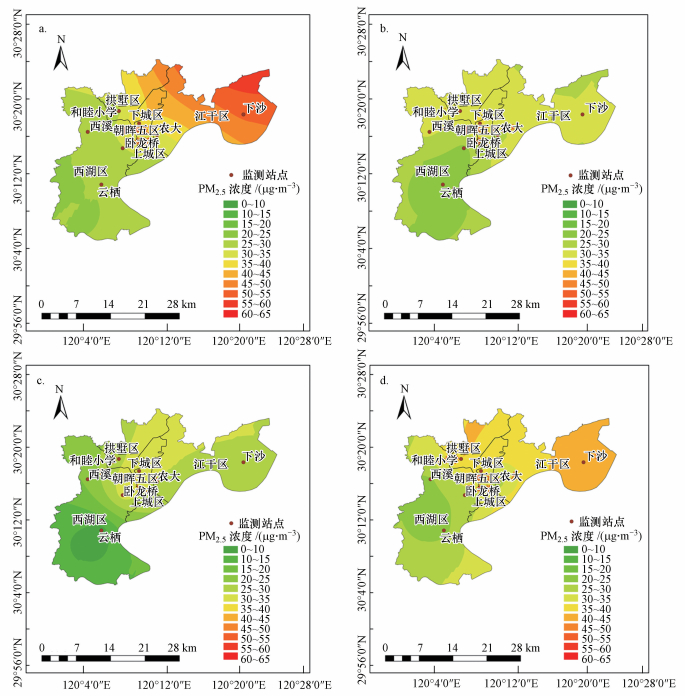图 5 夏季第40期(a)、80期(b)和冬季第40期(c)、80期(d)的PM2.5浓度预测结果 Fig. 5The PM2.5 concentration prediction map of 40th(a), 80th(b) periods in summer and 40th(c), 80th(d) periods in winter respectively

5 结论(Conclusions)1) SARIMA模型广泛运用于季节尺度的时间序列预测中, 但本研究创新性地将SARIMA模型广义化, 运用到以天为周期的小尺度季节时间序列中, 能较为准确地预测了杭州市主城区短期PM_2.5浓度的变化, 由于SARIMA模型基于内在的序列相关性变化, 对于极端外在因素影响的剧烈变化预测效果不好, 但因为模型简单, 计算速度快, 短期预测也相对准确, 在夏季和冬季, 总体PM_2.5浓度预测平均绝对误差(MAE)为分别8.0 μg·m^-3和14.8 μg·m^-3, 所以对于PM_2.5相对变化稳定的时间段内, 可以利用该方法对PM_2.5浓度的趋势进行短期预报, 也可以为城市管理者进行大气污染预警和治理提供决策支持.
2) 本研究通过滚动更新数据, 机器学习以最小AIC的方法建立SARIMA模型, 并利用普通Kriging法进行空间插值, 这种PM_2.5浓度预测方法不仅可以批量自动化, 而且将预测数据可视化来让市民更加直观清楚地了解PM_2.5的预测空间分布, 可为今后的预测制图产品化提供技术支持.未来, 也可以用该方法运用到其他城市或是更大范围的PM_2.5浓度预测的实际业务中.

参考文献

Akaike H. 1987. Factor analysis and AIC[J]. Psychometrika, 52: 317–332.DOI:10.1007/BF02294359

弓小平, 杨毅恒. 2008. 普通Kriging法在空间插值中的运用[J]. 西北大学学报(自然科学版), 2008, 38(6): 878–882.

龚明, 叶春明. 2016. 基于修正灰色马尔科夫链的上海市PM2.5浓度预测[J]. 自然灾害学报, 2016, 25(5): 97–104.

郭丹, 胡博, 刘俊德, 等. 2016. 基于SARIMA模型的风电场月发电量预测研究[J]. 中国电力, 2016, 49(2): 136–140.DOI:10.11930/j.issn.1004-9649.2016.02.136.05

Kumar U, Jain V K. 2010. ARIMA forecasting of ambient air pollutants (O3, NO, NO2 and CO)[J]. Stochastic Environmental Research and Risk Assessment, 24: 751–760.DOI:10.1007/s00477-009-0361-8

李瑞法, 柳之光, 楚伟, 等. 2016. 我国进境植物疫情截获量的时序特征及预测[J]. 植物检疫, 2016, 30(4): 1–5.

梁文娟, 程明. 2016. SARIMA模型在航空公司运营安全状态预测中的应用[J]. 安全与环境学报, 2016, 16(3): 20–24.

刘小生, 李胜, 赵相博. 2013. 基于基因表达式编程的PM2.5浓度预测模型研究[J]. 江西理工大学学报, 2013, 34(5): 1–5.

马天成, 刘大铭, 李雪洁, 等. 2014. 基于改进型PSO的模糊神经网络PM2.5浓度预测[J]. 计算机工程与设计, 2014, 35(9): 3258–3262.

Peiris M S, Perera B J C. 1988. On prediction with fractionally differenced arima models[J]. Journal of Time Series Analysis, 9: 215–220.DOI:10.1111/j.1467-9892.1988.tb00465.x

乔改瑞, 蔡会武, 周安宁, 等. 2016. 基于Kriging插值法的钻孔煤煤质预测模型研究[J]. 煤炭技术, 2016(2): 151–153.

苏姝, 林爱文, 刘庆华. 2004. 普通Kriging法在空间内插中的运用[J]. 江南大学学报, 2004, 3(1): 18–21.

陶长余, 张志兰. 2016. 应用SARIMA模型预测南通市流行性腮腺炎发病趋势[J]. 中国卫生统计, 2016, 33(1): 142–143.

王黎明, 吴香华, 赵天良, 等. 2017. 基于距离相关系数和支持向量机回归的PM2.5浓度滚动统计预报方案[J]. 环境科学学报, 2017, 37(4): 1–11.

Wang W, Guo Y.2009.Air Pollution PM2.5 Data Analysis in Los Angeles Long Beach with Seasonal ARIMA Model[R].Proceedings of the 2009 International Conference on Energy and Environment Technology.7-10

吴兑. 2012. 近十年中国灰霾天气研究综述[J]. 环境科学学报, 2012, 32(2): 257–269.

谢永华, 张鸣敏, 杨乐, 等. 2015. 基于支持向量机回归的城市PM2.5浓度预测[J]. 计算机工程与设计, 2015, 36(11): 3106–3111.

杨仁东, 胡世雄, 邓志红, 等. 2016. 湖南省手足口病发病趋势SARIMA模型预测[J]. 中国公共卫生, 2016, 32(1): 48–52.DOI:10.11847/zgggws2016-32-01-15