全文HTML
--> --> --> 钢铁行业能源消耗巨大,在钢铁加工制造过程中会产生大量颗粒物[1-3]。我国日益提高的环境标准,为颗粒物的有效处理提出了新的要求[4]。目前,纤维捕集技术是最有效的颗粒物处理手段之一,被广泛应用在工业中[5]。Davies孤立圆柱理论是纤维捕集颗粒物理论的基础[6]。随着工业技术的进步,纤维截面的形状已经产生了2类变化:截面形状的非圆化,包括截面形状轮廓波动的异形化和截面直径不对称的异形化;截面的中空和复合化[7]。纤维截面形状的变化使得纤维捕集颗粒物的效率也得以提升。针对不同截面形状的颗粒物捕集纤维,国内外****进行了相关研究。孙熙等[8]通过数值分析的方法求解矩形纤维阻力,并分析了纤维层流场的特征,结果与理论求解结果相符合。王浩明等[9]通过使用格子Boltzmann法模拟了椭圆纤维捕集颗粒物的过程,发现相同体积分数下,椭圆纤维可有效提高扩散机制为主导的颗粒物捕集效率,而拦截机制或惯性碰撞机制为主导时的捕集效率与纤维放置方式有关。顾丛汇等[10]结合欧拉-拉格朗日法对“Y”形截面和圆形截面的单纤维进行了模拟,发现“Y”形纤维对颗粒物的截留效率高于圆形纤维。王坤等[11]使用格子Boltzmann法模拟了三角形、十字形及三叶形3种异形纤维捕集颗粒物的过程,发现扩散机制主导时捕集效率不受纤维放置方式影响,拦截机制和惯性机制主导时捕集效率均受纤维放置方式影响。杨会等[12]采用数值方法求解绕方形纤维截面纤维流场,考虑了布朗扩散、拦截效率和惯性碰撞3种捕集机理的联合作用,研究了方形截面纤维的过滤性能,发现方形纤维对以扩散捕集机制为主的小粒子和惯性捕集机制的大粒子在纤维表面表现出显著的局部沉积特征,并与方形纤维的迎风角度有关,而方形截面纤维对颗粒物的捕集性能与填充率有关。RAYNOR[13]通过数值计算的方法求解了椭圆纤维表面的流动特征并与理论计算结果进行了对比,验证了数值计算的可靠性。HOSSEINI等[14]模拟了圆形纤维、方形纤维、椭圆形纤维和三叶形纤维4种截面形状纤维结构,并考虑了纳米纤维表面的滑移效应,对比分析了4种截面形状纤维捕集颗粒物的性能,结果表明,纤维形状对纳米纤维性能的影响大于微米级纤维。FOTOVATI等[15]模拟研究了三叶形纤维捕集颗粒物的性能,得出了三叶形纤维捕集效率与三叶形纤维内切圆和外接圆之比的关系。SALEH等[16]的模拟研究表明,三叶形纤维的捕集效率和颗粒物在纤维表面的沉积特性受其纤维放置方式的影响较明显。HUANG等[17]模拟了长方形、三叶形、四叶形和三角形4种异形纤维的颗粒物捕集效率,发现异形纤维对亚微米颗粒物的捕集效率更高。HUANG等[18]发现,颗粒物会在椭圆形纤维表面均匀沉积,并最终形成树枝状结构。
现有对不同横截面形状纤维的研究,多集中在单一横截面形状。为了探究横截面形状多角形变化方式对纤维捕集颗粒物性能的影响,有必要对横截面形状为正多边形的异形纤维进行模拟研究。目前,计算流体力学(computational fluid dynamics, CFD)发展迅速,Fluent是目前比较常见的商用CFD软件包,可用来模拟流体[19]、热传递[20]及化学反应[21]等,其中内置的离散相模型(discrete phase model, DPM)在拉格朗日坐标系下求解颗粒物微分方程,并计算离散相的颗粒轨道,经常用于模拟颗粒物捕集与沉积[22]、液滴的干燥[23]、颗粒燃烧[24]等。
本研究从横截面为正多边形的纤维入手,探究纤维截面形状变化对单纤维捕集颗粒物效率的影响,从颗粒物粒径、入口风速、填充率和纤维放置方式等方面考察了不同横截面形状纤维捕集颗粒物的性能,为纤维的优化设计提供参考,以提高异形纤维对颗粒物的捕集效率。
1.1. 气固两相流模型
对于内部气-固两相流动进行模拟需要先计算气相场。文中采用层流(Laminar)、稳态(Steady)及不可压缩模型进行数值模拟。控制方程[25](连续性方程、动量方程)见式(1)和式(2)。式中:v为流体的速度,m·s?1;μ为流体的动力黏度, Pa·s;p为计算单元的压力,N。
采用二阶迎风格式SIMPLE算法对离散化动量方程进行压力速度耦合求解,并将各项收敛残差均设定在10?6。颗粒物采用面(surface)注入的方式进入流场,注入的颗粒总数为5 000个。假定颗粒物在流场中作无旋运动。颗粒物采用标准球形颗粒,粒径为0.5~2.5 μm。假设只考虑曳力和重力,而忽略了其他力的作用,颗粒物的受力平衡方程[25]见式(3)。
式中:g为重力加速度,m·s?2:ρ为流体密度,kg·m?3:Fother为颗粒物运动过程所受其他可以忽略的力,N。
1.2. 计算模型与边界条件
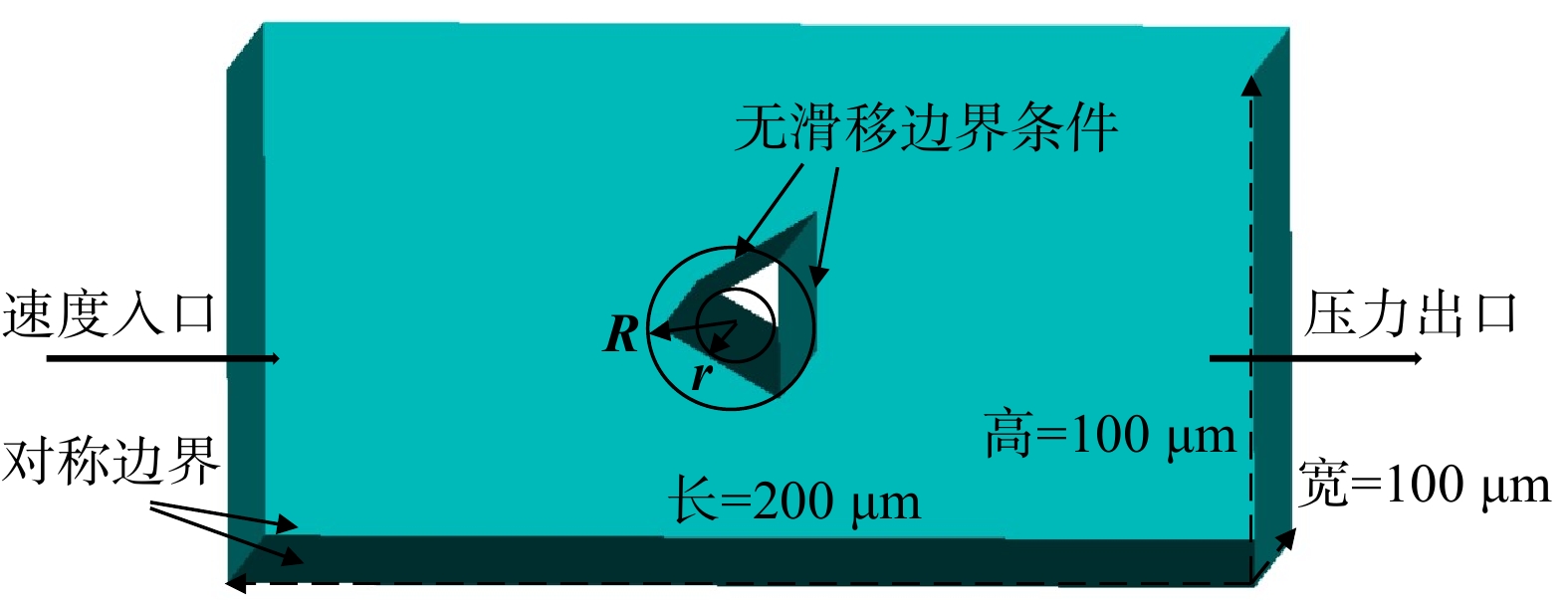
为考察异形纤维的颗粒物捕集性能,建立了不同横截面形状的纤维模型。计算域(Domain)入口处设置为速度入口边界条件(Velocity-inlet),出口设置为压力出口(Pressure-outlet),四周壁面设置为对称边界(Symmetry),如图1所示。以直径为20 μm的圆柱形纤维为标准,保证其相同的横截面积,建立了横截面为正多边形的异形纤维模型,如图2所示。纤维的放置方式分为2种:1)异形纤维的角平分线与气流方向平行,异形纤维的边线与气流方向呈钝角,如图3(a);2)异形纤维的边垂线与气流方向平行,异形纤维的边线与气流方向垂直,如图3(b)。由于所采用的纤维直径远大于空气分子的平均自由程,纤维表面不会发生滑移现象,故纤维表面采用无滑移壁面条件(No-slip boundary condition),计算域的长(L)、宽(W)、高(H)分别为200 μm、100 μm、100 μm。对于纤维截面的轮廓波动异形,采用纤维的径向异形度、截面异形度和圆周系数3个无量纲参数来表示纤维截面形状的变化[7],计算式为式(4)~(6)。
式中:Dr为纤维径向异形度;R为最多接触点的外接圆半径,m;r为内切圆半径,m;Sr为纤维截面异形度;H为纤维周长系数;L为纤维截面的周长,m;S为纤维的实际截面积,m2。经计算,常见的几种不同几何截面纤维的径向异形度、截面异形度和形状系数如表1 所示。
1.3. 网格独立性的验证
为去除网格因素对模拟结果的影响,对所使用的模型网格进行了独立性检验。对于低雷诺数不压缩黏性流体来说,气体在过滤器中的流动应当满足Darcy方程[26](式(7))。多纤维系统的压降与入口速度之比为一个常数,通常把这一比值认定为纤维所受曳力。KUWABARA[27]和HAPPEL[28]分别给出无量纲曳力与纤维层填充率的关系式,如式(8)和式(9)所示。式中:F1为Darcy方程给出的无量纲曳力表达式[26];F2为KUWABARA[27]提出的无量纲曳力关于纤维层填充率α的表达式;F3为HAPPEL[28]给出的纤维层流动时的无量纲曳力关于纤维层填充率α的表达式;Z为纤维层厚度, m;α为纤维层的体积分数[27],α= d2f·H?2;df为纤维直径, m;Δp为纤维层实际压降, Pa。
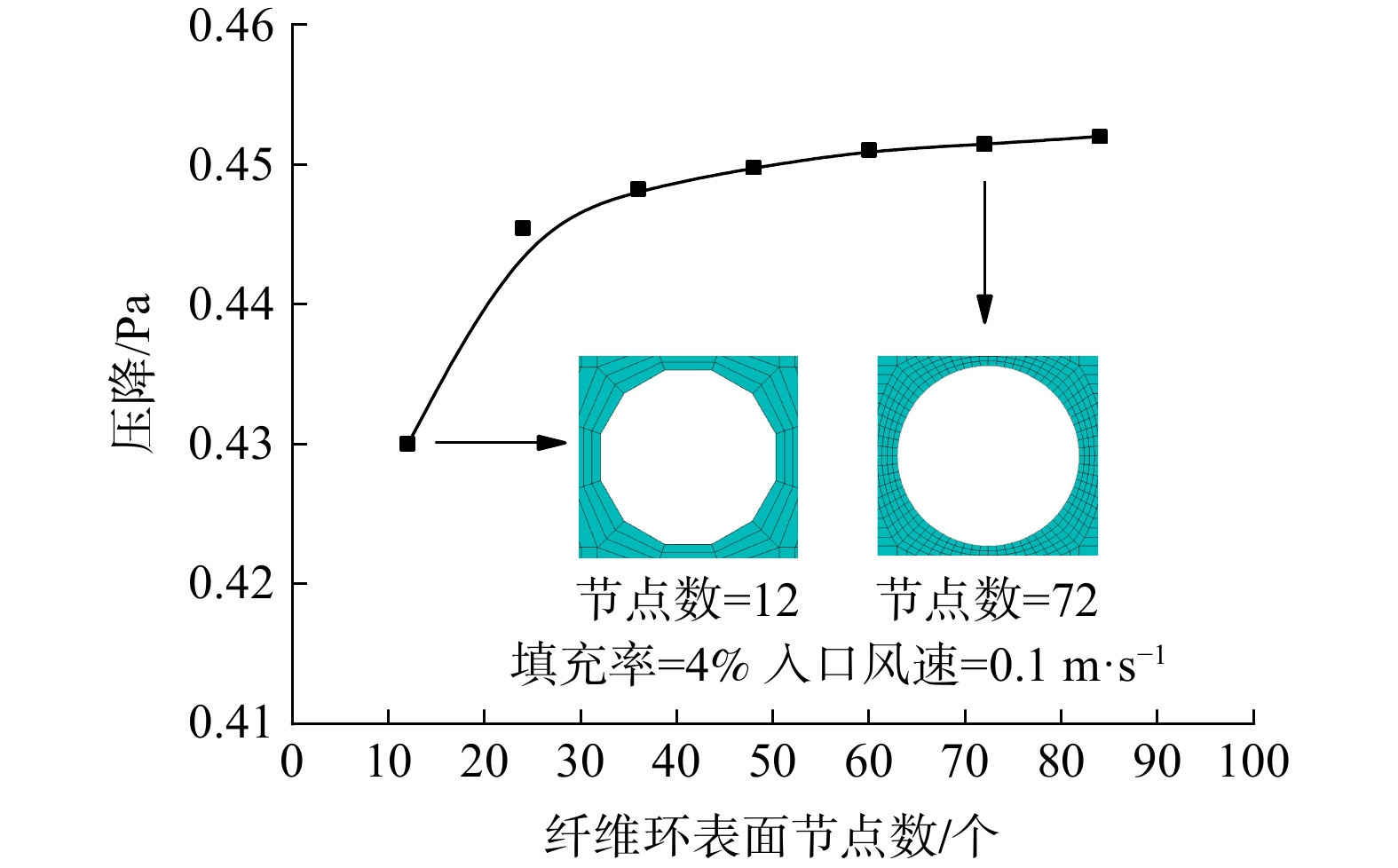
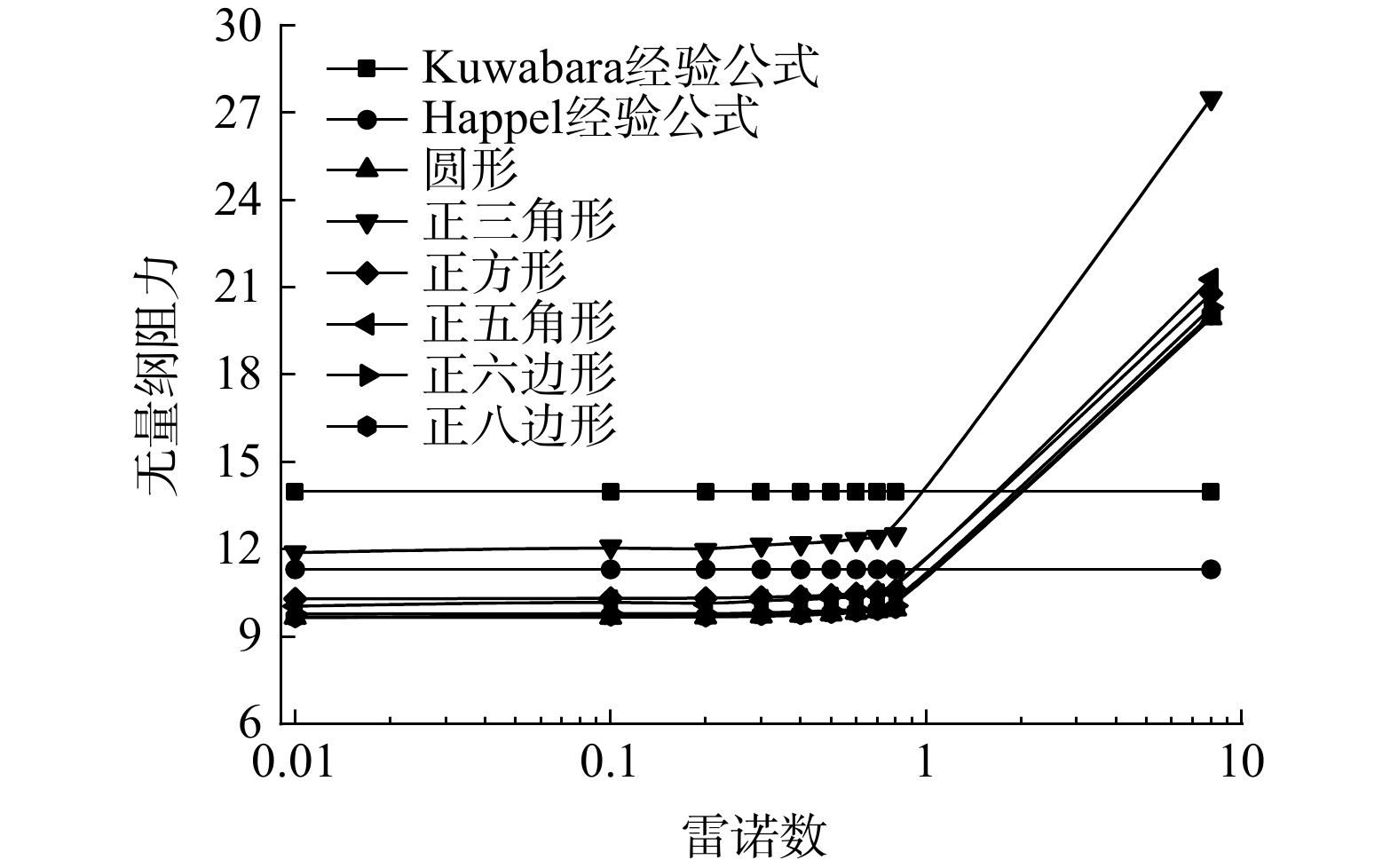
LIU等[29]进一步研究后发现,纤维的雷诺数(Re=ρvdf/μ)等于1时是纤维压力损失一个重要节点。当Re数大于1时,F1值开始随Re数升高而升高;Re数小于1时,F1值为定常数,模拟结果应符合此规律。图4为圆形单纤维压力损失变化与纤维环网格结点数变化之间的关系。纤维的填充率为4%,入口风速为0.1 m?s?1,纤维表面结点总数从12个增加到84个纤维表面结点总数大于等于60时,纤维的压力损失趋于稳定。本研究所建立的异形纤维模型的表面网格密度均与圆形单纤维表面网格密度相同。所有网格均采用六面体结构化网格,并对纤维表面部分进行加密处理,网格质量均大于0.7。图5为数值模拟结果与经验公式对比图,网格质量符合数值模拟要求,因此,文中所采用的网格可准确表示纤维表面的流动特点。
为验证纤维对颗粒物捕集效率的准确性,计算了单纤维模型捕集颗粒物的效率,并与经验公式进行了对比。不考虑布朗运动时,单纤维的捕集效率有多种计算方式。式(10)、(11)分别为Davies经验公式[6]及其修正式。由于本研究没有考虑布朗力的作用,故忽略布朗力作用下,单纤维对颗粒物的捕集效率也可用式(12)表示[30]。
式中:η为纤维捕集效率,%;Rp为直接碰撞系数;St为斯托克斯数;η0为修正后单纤维的捕集效率,%;ηt为单纤维在惯性碰撞和拦截机制下的总捕集效率,%;ER为单纤维的拦截捕集效率,%;EI为单纤维惯性碰撞捕集效率,%。模拟结果采用式(15)进行计算[31]。图6表明,横截面为圆形的单纤维在填充率为4%时,模拟结果与经验公式相近,在误差允许范围内。
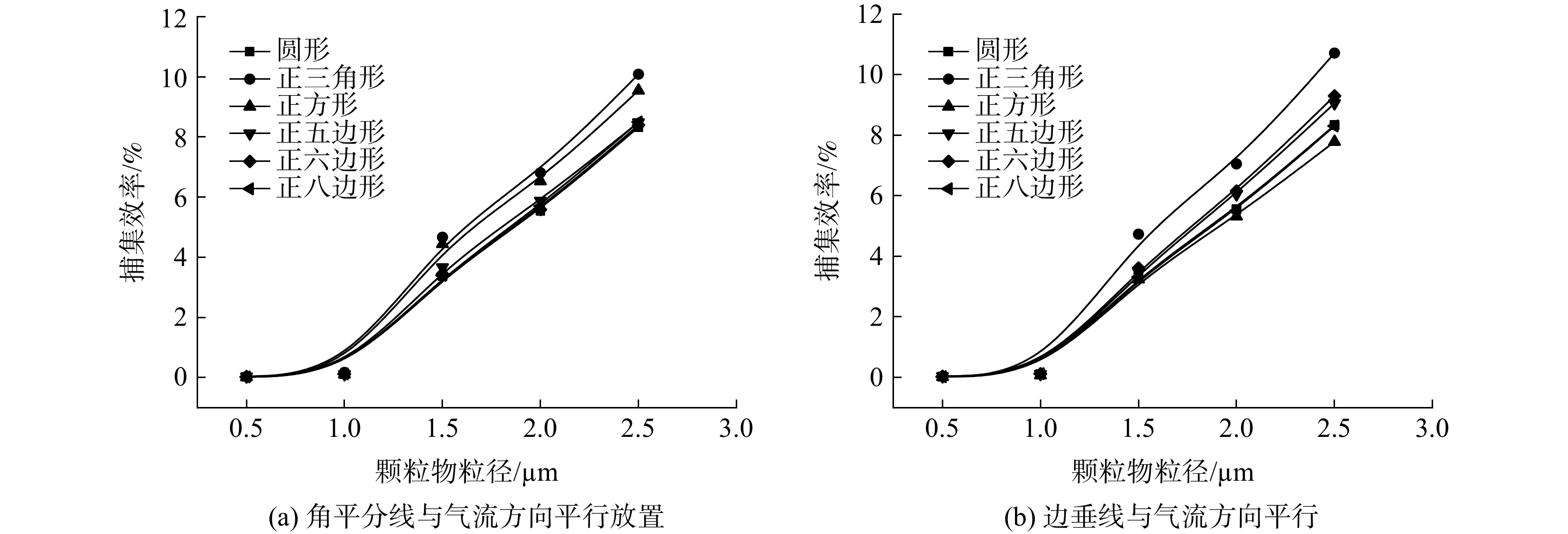
2.1. 粒径对异形纤维捕集颗粒物效率的影响
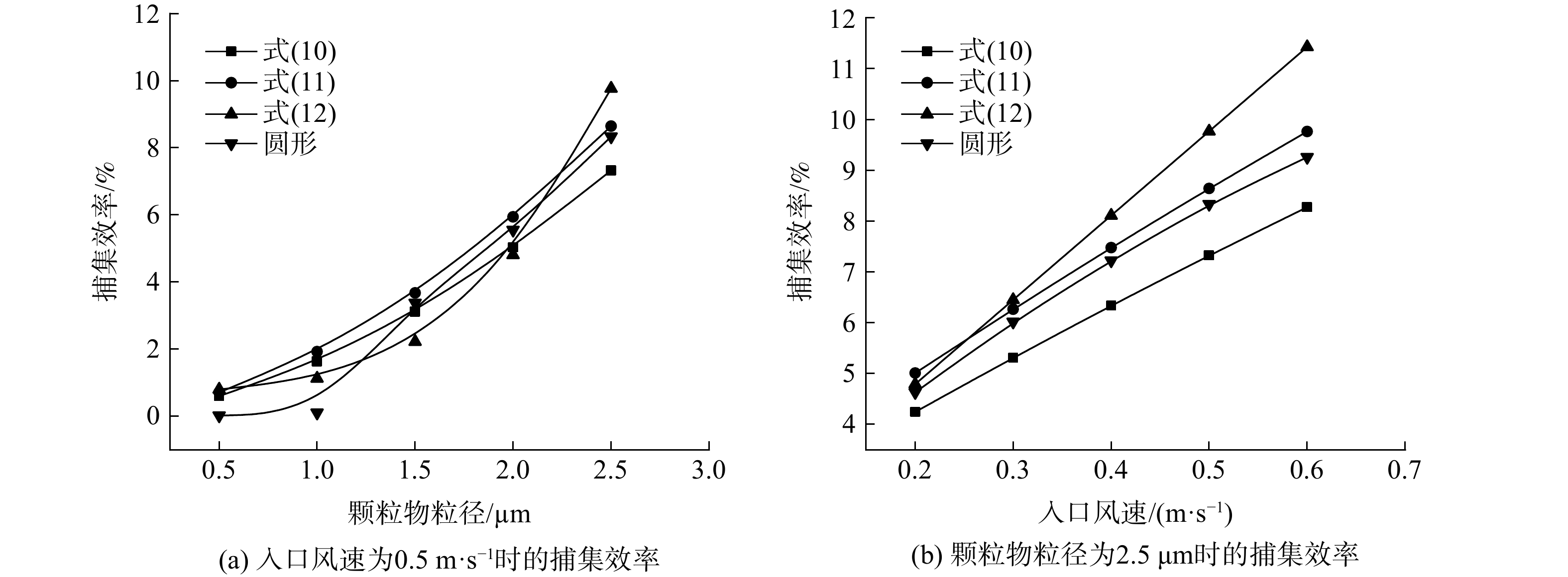
图7 为不同异形纤维在填充率为4%、入口风速为0.5 m·s?1时,对粒径为0.5~2.5 μm颗粒物的捕集效率。由图7可知,捕集效率随颗粒物粒径的增加而增加。图7(a)中异形纤维的放置方式同图3(a),与横截面形状为圆形的纤维相比,三角形纤维和四边形纤维均有效提高了单纤维对粒径为1.5~2.5 μm颗粒物的捕集效率。其中,三角形纤维的捕集效率最大。图7(b)中异形纤维的放置方式同图3(b),只有三角形纤维有效提高了单纤维对粒径为1.5~2.5 μm颗粒物的捕集效率。这是因为:纤维的外接圆直径增加,导致直接碰撞系数增加,拦截机制下的捕集效率相应增加,同时气流绕柱流动的轨迹发生改变,从而提高了惯性碰撞机制下的捕集效率。对比2种放置方式下异形纤维对颗粒物的捕集效率,发现三角形纤维和正五边形纤维在捕集粒径为1.5~2.5 μm的颗粒物时,以图3(a)方式放置的捕集效率高于以图3(b)方式放置的捕集效率。其中,方形纤维对颗粒物的捕集效率受纤维放置方式影响最大。这是由于:2种放置方式影响了方形纤维迎风横截面积的大小,故方形纤维的捕集效率受放置方式的影响最大。异形纤维对粒径为0.5~1.0 μm的颗粒物捕集效率没有明显提高。这是因为拦截和惯性碰撞2种捕集机制对小粒径颗粒的作用不明显,所以其捕集效率没有明显增加。
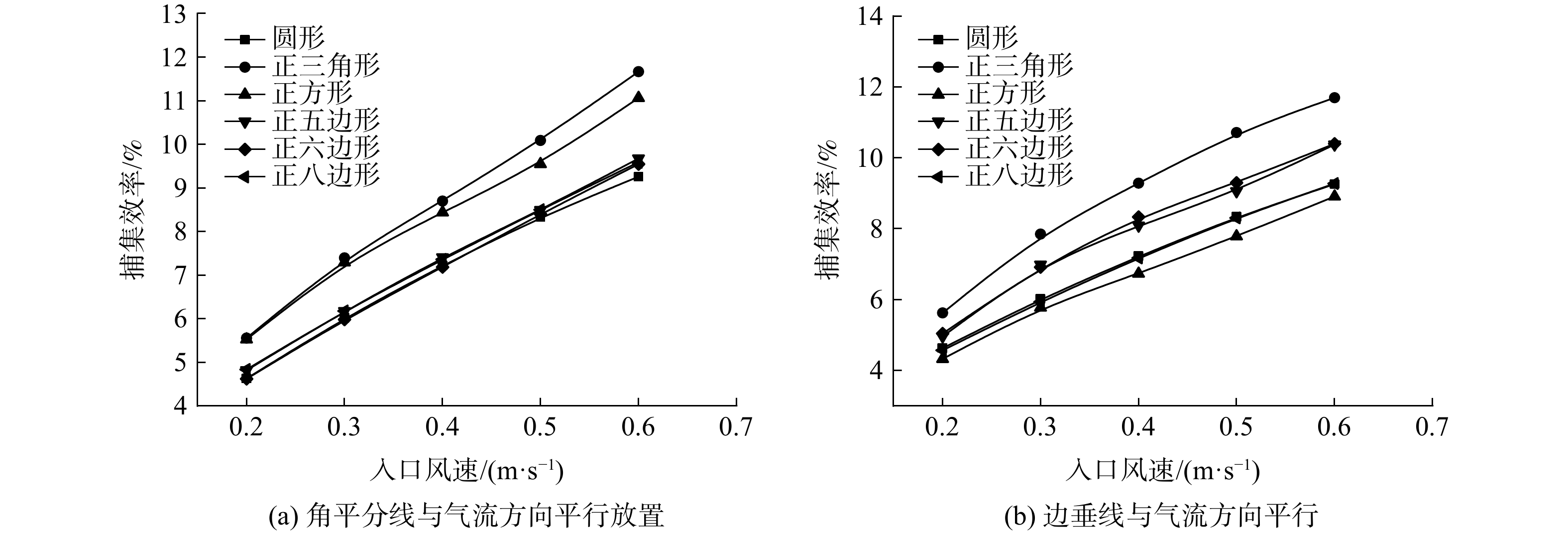
2.2. 入口风速对异形纤维捕集颗粒物效率的影响
图8 是填充率为4%、颗粒物粒径为2.5 μm,入口风速为0.2~0.6 m·s?1时,不同异形纤维对颗粒物的捕集效率。可以看出,异形纤维对颗粒物的捕集效率随入口风速的增加而增加。图8(a)中异形纤维以图3(a)方式放置,与横截面为圆形的纤维相比,三角形和方形纤维在不同风速下对粒径为2.5 μm颗粒物的捕集效率均有提升。图8(b)中异形纤维以图3(b)方式放置。与圆形纤维相比,在不同风速下,三角形纤维、五边形纤维和六边形纤维对粒径为2.5 μm颗粒物的捕集效率均有提高 。这是因为:入口风速增加时,虽然直接碰撞系数不变,但颗粒物的斯托克斯数增加,导致惯性碰撞机制的捕集效率增加,故纤维的捕集效率增加。三角形和五边形纤维在入口风速为0.2~0.6 m·s?1,捕集粒径为2.5 μm的颗粒物时,以图3(a)方式放置的异形纤维对颗粒物的捕集效率高于以图3(b)方向方式放置的异形纤维。这是因为纤维截面形状对气流绕柱流动轨迹的改变会导致惯性碰撞机制捕集效率产生差异,纤维的捕集效率亦会产生差异。六边形和八边形纤维对颗粒物的捕集效率与圆形纤维相比,没有明显提高。2.3. 填充率对异形纤维捕集颗粒物效率的影响
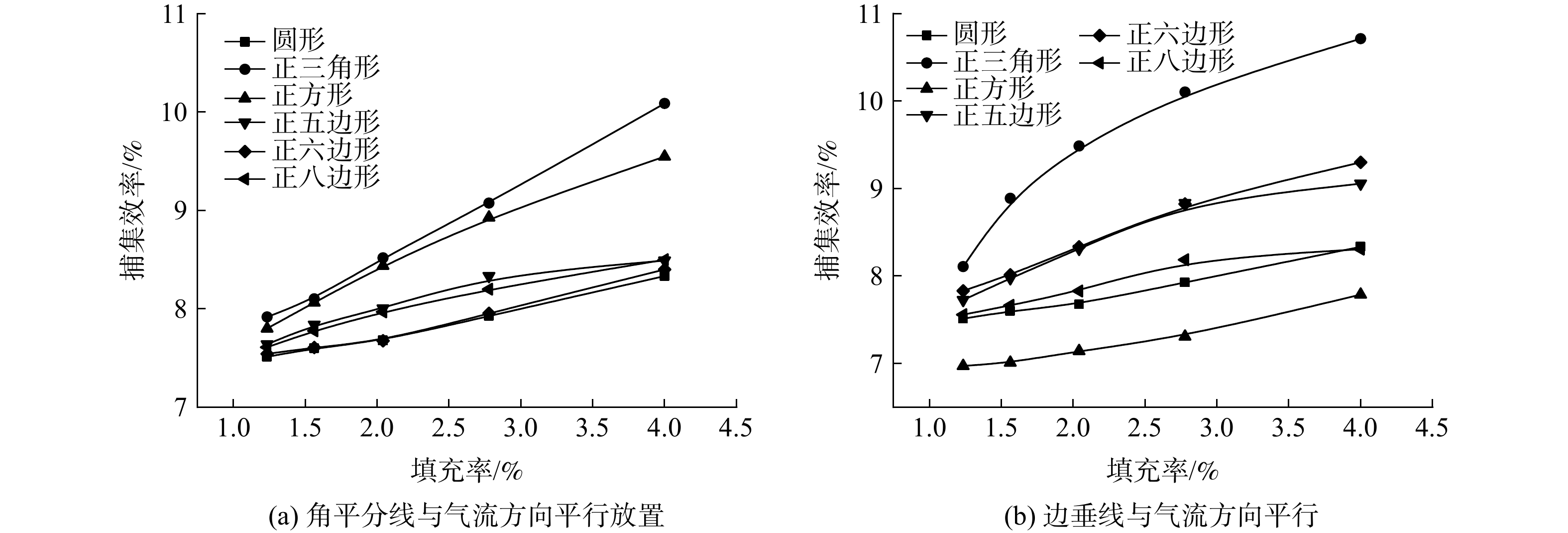
图9为异形纤维在填充率为1.2%~4.0%时,对入口风速为0.5 m·s?1的粒径为2.5 μm颗粒物的捕集效率。该图表明,异形纤维对颗粒物的捕集效率随填充率增加而增加。图9(a)中异形纤维以图3(a)的方式放置,与横截面为圆形的纤维相比,三角形纤维和方形纤维有效提高了纤维对粒径2.5 μm颗粒的捕集效率。图9(b)中异形纤维以图3(b)方式放置,与圆形纤维相比,三角形纤维有效提高了纤维对粒径为2.5 μm颗粒的捕集效率。五边形纤维和六边形纤维捕集颗粒物的效率均高于圆形纤维,但低于三角形纤维。2)异形纤维对颗粒物的捕集效率受放置方式的影响,对于相同迎风横截面积的异形纤维,以异形纤维边的中点与形心连线方式放置的异形纤维对颗粒物的撑捕集效率大于以顶角与形心连线的捕集效率。因此,相同迎风截面的异形纤维应采用边迎风的方式来提高异形纤维对颗粒物的捕集效率。
3)不同放置方式的异形纤维对颗粒物捕集性能受异形纤维径向异形度的影响,径向异形度越小,异形纤维对颗粒物的捕集效率越低,且受放置方式的影响也越小,其中方形纤维对颗粒物的捕集效率受放置方式影响最大。
参考文献
 下载:
下载: 

 点击查看大图
点击查看大图