含弹性应变能的各向异性相场模型的指数时间差分方法

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-02

王姗姗^,¹^,², 张鉴^,¹^,^*

1. 中国科学院计算机网络信息中心,北京 100190

2. 中国科学院大学,北京 100049

Exponential Time Difference Method for Anisotropic Phase Field Model with Elastic Strain Energy

Wang Shanshan^,¹^,², Zhang Jian^,¹^,^*

1. Computer Network Information Center,Chinese Academy of Sciences, Beijing 100190, China

2. University of Chinese Academy of Sciences, Beijing 100049, China

通讯作者: 张鉴（E-mail:zhangjian@sccas.cn）

收稿日期:2020-03-2网络出版日期:2020-06-20

基金资助:

国家重点研发计划项目.2016YFB0201100
国家重点研发计划项目.2017YFB0202803
国家自然科学基金资助项目.11871454
国家自然科学基金资助项目.91630204
国家自然科学基金资助项目.61531166003
中国科学院战略性先导科技专项(B类).XDB22020102
中国科学院信息化专项.XXH13506-204

Received:2020-03-2Online:2020-06-20
作者简介 About authors

王姗姗,中国科学院计算机网络信息中心,中国科学院大学,硕士研究生,主要研究方向为高性能计算、相场模拟。
本文承担工作为：指数时间差分方法的求解格式与能量稳定性的证明,以及数值实验的实现。
Wang Shanshan is a graduate student at Computer Network Information Center of the Chinese Academy of Sciences, University of Chinese Academy of Sciences. Her main research directions are high performance calculation and phase field simulation.
In this paper, she undertakes the following work: the solution scheme of the Exponential Time Difference method, the proof of the energy stability, and the realization of the numerical experiment.
E-mail: wangshanshan@cnic.cn

张鉴,中国科学院计算机网络信息中心,研究员,博士生导师,主要研究方向为高性能计算、偏微分方程数值算法和并行算法研究。
本文承担工作为：指数时间差分方法以及相场数值模拟实验的指导。
Zhang Jian is a research fellow and the Ph.D. supervisor at Computer Network Information Center of the Chinese Academy of Sciences. His main research fields are high performance computing, PDE numerical algorithm and parallel algorithm.
In this paper, he undertakes the following tasks: guidance of the Exponential Time Difference method and the phase field numerical simulation experiment.
E-mail: zhangjian@sccas.cn

摘要
【目的】材料微结构中界面能异性和弹性应变能是产生各向异性的主要因素,本文主要研究含弹性应变能的各向异性相场模型的紧致指数时间差分方法。【方法】在紧致指数时间差分方法框架下引入了界面能异性和弹性应变能的计算,将界面能异性和弹性应变能归于指数时间差分方法的非线性项统一处理,为二者设计了算子分裂格式。【结果】从数学上证明了算子分裂格式能够保证能量稳定,并进行了镍基合金以及Zr的氢化物的材料腐蚀相场模型的数值实验,验证了含弹性应变能的各向异性相场模型的指数时间差分方法的能量稳定性。【局限】本文仅得到了指数时间差分方法的一阶和二阶求解格式,更高阶的求解格式有待进一步探索。【结论】设计了能量稳定的含弹性应变能的各向异性相场模型的指数时间差分方法。
关键词： 相场模型;紧致指数时间差分方法;界面能异性;弹性应变能

Abstract
[Objective] The interface energy and elastic strain energy are the main factors of anisotropy in the microstructure of materials. In this paper, the compact Exponential Time Difference method of anisotropic phase field model with elastic strain energy is studied. [Methods] In the framework of the compact Exponential Time Difference method, the calculation of interface energy and elastic strain energy is introduced. The interface energy and elastic strain energy are treated as the nonlinear terms of the Exponential Time Difference method, and the operator splitting scheme is designed for them. [Results] It is mathematically proved that the operator splitting scheme can guarantee the energy stability, and the numerical experiments of the corrosion phase field model of Ni-based alloy and Zr-hydride are carried out, which verify the energy stability of the Exponential Time Difference method of the anisotropic phase field model with elastic strain energy. [Limitations] In this paper, only the first-order and second-order solutions of the Exponential Time Difference method are obtained, and the higher-order solutions need to be further explored. [Conclusions] The Exponential Time Difference method of energy stable anisotropic phase field model with elastic strain energy is designed.
Keywords：phase field model;Compact Exponential Time Difference Method;interfacial anisotropy;elastic strain energy

PDF (8283KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
王姗姗, 张鉴. 含弹性应变能的各向异性相场模型的指数时间差分方法. 数据与计算发展前沿[J], 2020, 2(3): 113-125 doi:10.11871/jfdc.issn.2096-742X.2020.03.010
Wang Shanshan, Zhang Jian. Exponential Time Difference Method for Anisotropic Phase Field Model with Elastic Strain Energy. Frontiers of Data and Computing[J], 2020, 2(3): 113-125 doi:10.11871/jfdc.issn.2096-742X.2020.03.010

引言

相场法是近年来出现的一种强有力的计算方法,用于建模和预测材料的中尺度形态和微观结构演变^[1]。相场法使用一组守恒和非守恒的在区域内连续的场变量来描述微观结构。经典的相场方程——Allen-Cahn方程^[2]和Cahn-Hilliard方程^[3],描述了场变量在空间和时间上的改变。微观结构的繁杂演化可以被相场法有效的描述,而无需明确跟踪界面的位置。相场法已成为模拟中尺度微观结构演化的一种重要而通用的方法。

对于经典的Allen-Cahn方程和Cahn-Hilliard方程,已有基于有限差分格式的时间推进求解方案。这些求解方案普遍存在着缺陷：很难设计高阶的求解格式、时间步长无法取到令人满意的长度等。本文所使用的紧致指数时间差分方法（compact Exponential Time Difference, cETD）^[4,5],对于经典的相场方程的高阶导数项,采用积分因子法进行准确积分,而对于它们的非线性项,又与经典的积分因子法不同,紧致指数时间差分方法对方程的非线性部分利用多步逼近、龙格库塔、预估校正等方法设计了高阶的求解格式,并且利用算子分裂格式增强了整体的稳定性。

微观结构演化的动力是系统的总能量下降,系统的总自由能包括化学自由能、界面能、弹性应变能、电磁能、静电能等。其中,界面能各向异性和弹性应变能是材料产生各向异性的主要因素。界面能是微结构的界面上由于组成和结构的不均匀产生的额外的能量,由于固体的晶体性质,界面能通常是各向异性的,界面能各向异性的程度可以对粒子的生长形态和平衡形状产生重大影响,在相场方程中,界面能各向异性表现为包含非线性系数的高阶空间导数。弹性应变能产生于微结构中相之间的晶格失配造成弹性位移,通过Khachaturyan 理论^[6]在相场方程中引入弹性应变能,将弹性应变能表达为场变量的函数。已有的关于弹性应变能计算的工作^[7,8],多为使用显格式进行计算的。

本文研究的重点是紧致指数时间差分方法中界面能各向异性和弹性应变能的计算。化学自由能在相场方程中主要表现为高阶空间导数部分,已有的紧致指数时间差分方法通过适当算子分裂格式处理化学自由能,将其归于非线性项的计算,并证明了能量稳定性^[9,10,11]。本文在紧致指数时间差分方法框架下引入了界面能各向异性和弹性应变能的计算,将界面能各向异性和弹性应变能同样归于紧致指数时间差分方法的非线性项统一处理,为其设计了适当的算子分裂格式,证明了算子分裂能够保证能量稳定。并通过镍基合金以及Zr的氢化物的材料腐蚀相场模型的数值实验,验证了该算法的正确性和能量稳定性。

本文的组织结构如下,第一章介绍了相场模型中界面能各向异性和弹性应变能的引入;第二章主要阐述了含有界面能各向异性和弹性应变能的相场模型的紧致指数时间差分方法,进行了算子分裂格式的能量稳定性以及求解格式的时间精度的证明;第三章给出了镍基合金和Zr的氢化物材料腐蚀相场模型的数值实验,并验证了求解格式的时间精度;第四章对本文所采用的含弹性应变能的各向异性相场模型的指数时间差分方法进行了总结。

1 含弹性应变能的各向异性相场模型

在本文中,我们考虑含有界面能各向异性和弹性应变能的耦合模型能量方程如式(1.1)所示。

(1.1)

E = E_{c} + E_{el}

其中,E是系统的总能量,这里考虑了总能量中的化学自由能

E_{c}

和弹性应变能

E_{el}

。化学自由能

E_{c}

可以表达为界面梯度能量项和局部自由能量密度

f_{local} (c, η)

的积分,如式（1.2）所示,其中界面梯度能量中含有各向异性。式(1.2)中,c是成分场变量,而

η

为序参数,

α

和

β

是界面梯度能量项的系数,

Λ

是3x3的界面能各向异性矩阵,

f_{local} (c, η)

是关于场变量的多项式形式的局部能量密度,因此局部能量密度公式可导,局部能量密度公式关于两种场变量的偏导数如式(1.3)所示。

(1.2)

E_{c} = \int_{v} [\frac{1}{2} {|? c|}^{2} + \frac{1}{2} β {(? η)}^{T} Λ (? η) + f_{local} (c, η)] dr

其中,

Λ = [\begin{matrix} λ_{11} & λ_{12} & λ_{13} \\ λ_{21} & λ_{22} & λ_{23} \\ λ_{31} & λ_{32} & λ_{33} \end{matrix}]

(1.3)

\{\begin{matrix} f_{c} = \frac{? f_{local} (c, η)}{? c} \\ f_{η} = \frac{? f_{local} (c, η)}{? η} \end{matrix}

根据 Khachaturyan理论,在傅里叶空间中,弹性应变能的计算如式(1.4)的积分所示,相场方程中的弹性应变能部分如式(1.5)所示,该项被表达为场变量c或

η

的函数,引入相场方程中,这里以弹性应变能为场变量c的函数进行说明,弹性应变能为场变量

η

的函数的情况与之类似。

(1.4)

E_{el} = \frac{1}{2} \int B (n) {θ (c)}_{k} \frac{d^{3} k}{{(2 π)}^{3}}

其中,

(1.5)

B (n) = C_{ijkl} ε_{ij}^{0} ε_{kl}^{0} - n_{i} σ_{ij}^{0} Ω_{jk} (n) σ_{kl} n_{l}

f_{el} = \frac{δ E_{el}}{δc} = {\{B (n) {\{θ (c)\}}_{k}\}}_{r}

B (n)

是傅里叶空间的弹性相互作用能,

θ

是场变量c的结构函数,与分子结构相关。 k是傅里叶空间的向量,单位向量

n = \frac{k}{|k|}

{}_{k}

表示傅里叶变换,

{}_{r}

表示傅里叶逆变换,在三维空间中,

C_{ijkl}

是一个由四维张量根据物质结构对称性得到的二维刚度矩阵,i、j、k、l分别取1-3的数值,

ε^{0}

是应变矩阵,刚度矩阵和应变矩阵决定了弹性应变能的大小和类型。应力矩阵

σ_{ij}^{0} = C_{ijkl} ε_{kl}^{0}

Ω_{ik}^{- 1} = C_{ijkl} n_{j} n_{l}

。

对总能量方程(1.1)进行变分求解,可以得到描述守恒场变量c的Cahn-Hilliard方程以及描述结构场变量

η

的Allen-Cahn方程两种方程组成的耦合方程。Cahn-Hilliard方程和Allen-Cahn方程的耦合方程如式(1.6)所示,其中Cahn-Hilliard方程中的M是迁移率,而Allen-Cahn方程中的L是扩散系数。

(1.6)

\{\begin{matrix} \frac{? c}{? t} = M ? \frac{δE}{δc} \\ \frac{? η}{? t} = - L \frac{δE}{δη} \end{matrix}

\{\begin{matrix} \frac{? c}{? t} = M (- α ?^{2} c + ? (f_{c} + f_{el})) \\ \frac{? η}{? t} = L (β ? Λ ? η - f_{η}) \end{matrix}

2 指数时间差分方法的求解格式与能量稳定的证明

2.1 指数时间差分方法的求解格式

下面对式(1.6)所示含弹性应变能的各向异性相场方程的紧致指时间差分算法进行推导。假设,模拟区域为空间：

Ω = \{x_{0} < x < x_{1}, y_{0} < y < y_{1}, z_{0} < z < z_{1}\}

将空间离散化,

Ω

划分成

N_{x} \times N_{y} {\times N}_{z}

的网格：

Ω_{h} = \{(x_{i}, y_{j}, z_{k}) = (x_{0} + {ih}_{x}, y_{0} + {jh}_{y}, z_{0} + {kh}_{z})\}

其中,

h_{x} = \frac{(x_{1} - x_{0})}{N_{x}}, h_{y} = \frac{(y_{1} - y_{0})}{N_{y}}, h_{z} = \frac{(z_{1} - z_{0})}{N_{z}}

且

0 \leq i \leq N_{x}, 0 \leq j \leq N_{y}, 0 \leq k \leq N_{z}

则有：

η_{ijk} \approx η (t, x_{i}, y_{j}, z_{k})

c_{ijk} \approx c (t, x_{i}, y_{j}, z_{k})

模拟区域采用周期边界条件^[9]。

为了保证能量稳定需要进行算子分裂,后文中对能量稳定的算子分裂格式取值进行了证明。这里直接引入化学自由能分裂算子

κ_{c}

和

κ_{η}

,弹性应变能分裂算子

κ_{el}

,界面能各向异性分裂算子矩阵

Κ

。算子分裂后的方程如式(2.1)所示。

(2.1)

\{\begin{matrix} \frac{? c}{? t} = M (\begin{matrix} - α ?^{2} c + (κ_{c} + κ_{el}) ? c \\ + ? (f_{c} + f_{el}) - (κ_{c} + κ_{el}) ? c \end{matrix}) \\ \frac{? η}{? t} = L (\begin{matrix} β ΚΔ η - κ_{η} η - f_{η} + κ_{η} η \\ - β ? (Κ - Λ) ? η \end{matrix}) \end{matrix}

其中,各项异性算子分裂的矩阵如下：

Κ = [\begin{matrix} k_{x} & 0 & 0 \\ 0 & k_{y} & 0 \\ 0 & 0 & k_{z} \end{matrix}]

定义二维的方阵G如下：

G_{P \times P} = {[\begin{matrix} \begin{matrix} \begin{matrix} - 2 & 1 & 0 \end{matrix} & 0 & \begin{matrix} ? & 0 & 1 \end{matrix} \\ \begin{matrix} 1 & - 2 & 1 \end{matrix} & 0 & \begin{matrix} ? & 0 & 0 \end{matrix} \end{matrix} \\ \begin{matrix} ? & ? & ? \end{matrix} \\ \begin{matrix} \begin{matrix} 0 & 0 & ? \end{matrix} & 0 & \begin{matrix} 1 & - 2 & 1 \end{matrix} \\ \begin{matrix} 1 & 0 & ? \end{matrix} & 0 & \begin{matrix} 0 & 1 & - 2 \end{matrix} \end{matrix} \end{matrix}]}_{P \times P}

则,矩阵A, B, C可以表示为：

A = \frac{1}{h_{x}^{2}} G_{N_{x} \times N_{x}}

B = \frac{1}{h_{y}^{2}} G_{N_{y} \times N_{y}}

C = \frac{1}{h_{z}^{2}} G_{N_{z} \times N_{z}}

定义运算：

{(A \overset{?}{x} U)}_{ijk} = \sum_{l = 1}^{N_{x}} {(A)}_{il} u_{ljk}

{(B \overset{?}{y} U)}_{ijk} = \sum_{l = 1}^{N_{y}} {(B)}_{jl} u_{ilk}

{(C \overset{?}{z} U)}_{ijk} = \sum_{l = 1}^{N_{z}} {(C)}_{kl} u_{ijl}

空间离散形式的拉普拉斯算子矩阵可以写成^[9]:

?_{h} = A \overset{?}{x} + B \overset{?}{y} + C \overset{?}{z}

将算子代入式(2.1),得到方程的空间离散形式如式(2.2)所示：

(2.2)

\{\begin{matrix} \frac{? c}{? t} = M (- α ?_{h}^{2} c + (κ_{c} + κ_{el}) ?_{h} c) \\ + M (?_{h} (f_{c} + f_{el}) - (κ_{c} + κ_{el}) ?_{h} c) \\ \frac{? η}{? t} = L (βΚ Δ_{h} η - κ_{η} η) \\ + L (- f_{η} + κ_{η} η - β ?_{h} ? (Κ - Λ) ?_{h} η) \end{matrix}

根据紧致指数时间差分方法的描述,这里将方程中含有高阶导数的线性项与含有局部能量密度、界面能各向异性、弹性应变能的非线性项g分离,得到式（2.3）。

(2.3)

\begin{matrix} \frac{? c}{? t} = M (- α ?_{h}^{2} c + (κ_{c} + κ_{el}) ?_{h} c) + g_{c} \\ \frac{? η}{? t} = L (βΚ Δ_{h} η - κ_{η} η) + g_{η} \end{matrix}

其中,

\{\begin{matrix} g_{c} = M (?_{h} (f_{c} + f_{el}) - (κ_{c} + κ_{el}) ?_{h} c) \\ g_{η} = L (- f_{η} + κ_{η} η - β ?_{h} ? (Κ - Λ) ?_{h} η) \end{matrix}

在紧致指数时间差分方法中,通过离散傅里叶变换^[12]来降低计算复杂度。将矩阵A,B,C根据特征值分解为如下形式：

A = P_{x} D_{x} P_{x}^{- 1}

B = P_{y} D_{y} P_{y}^{- 1}

C = P_{z} D_{z} P_{z}^{- 1}

其中,

\{\begin{matrix} D_{x} = diag [d_{1}^{x}, \dots, d_{N_{x}}^{x}], d_{k}^{x} = - \frac{2}{h_{x}^{2}} \sin^{2} \frac{(k - 1) π}{N_{x}}, \\ {(P_{x})}_{kj} = \exp ? \exp (- i \frac{2 π (k - 1) (j - 1)}{N_{x}}), k, j = 1, \dots, N_{x} \\ D_{y} = diag [d_{1}^{y}, \dots, d_{N_{y}}^{y}], d_{k}^{y} = - \frac{2}{h_{y}^{2}} \sin^{2} \frac{(k - 1) π}{N_{y}}, \\ {(P_{y})}_{kj} = \exp ? \exp (- i \frac{2 π (k - 1) (j - 1)}{N_{y}}), k, j = 1, \dots, N_{y} \\ D_{z} = diag [d_{1}^{z}, \dots, d_{N_{x}}^{z}], d_{k}^{z} = - \frac{2}{h_{z}^{2}} \sin^{2} \frac{(k - 1) π}{N_{z}}, \\ {(P_{z})}_{kj} = \exp ? \exp (- i \frac{2 π (k - 1) (j - 1)}{N_{z}}), k, j = 1, \dots, N_{z} \end{matrix}

定义算子：

D = D_{x} \overset{?}{x} {+ D}_{y} \overset{?}{y} + D_{z} \overset{?}{z}

T = {P_{z}}^{- 1} \overset{?}{z} {P_{y}}^{- 1} \overset{?}{y} {P_{x}}^{- 1} \overset{?}{x}

T^{- 1} = P_{z} \overset{?}{z} P_{y} \overset{?}{y} P_{x} \overset{?}{x}

代入式(2.3),可得式（2.4）,经推导后可得式(2.5)。

(2.4)

\{\begin{matrix} \frac{? Tc}{? t} + M (α D^{2} - (κ_{c} + κ_{el}) D) Tc = T g_{c} \\ \frac{? Tη}{? t} - L (β ΚD - κ_{η}) T η = T g_{η} \end{matrix}

(2.5)

\{\begin{matrix} \frac{? Tc}{? t} + H_{c} Tc = T g_{c} \\ \frac{? Tη}{? t} + H_{η} Tη = T g_{η} \end{matrix}

其中,

\{\begin{matrix} H_{c} = {(h_{c}^{ijk})}_{N_{x} \times N_{y} \times N_{z}}, \\ h_{c}^{ijk} = M (\begin{matrix} α {(d_{x}^{i} + d_{y}^{j} + d_{z}^{k})}^{2} \\ - (κ_{c} + κ_{el}) (d_{x}^{i} + d_{y}^{j} + d_{z}^{k}) \end{matrix}) \geq 0 \\ H_{η} = {(h_{η}^{ijk})}_{N_{x} \times N_{y} \times N_{z}}, \\ h_{η}^{ijk} = - L (β (k_{x} d_{x}^{i} + k_{y} d_{y}^{j} + k_{z} d_{z}^{k}) - κ_{η}) \geq 0 \end{matrix}

在紧致指数时间差分方法中,式(2.5) 需要与定义的如下指数时间因子相乘,

{(e^{*})}^{H_{c} t} = {(e^{h_{c}^{ijk} t})}_{N_{x} \times N_{y} \times N_{z}}

{(e^{*})}^{H_{η} t} = {(e^{h_{η}^{ijk} t})}_{N_{x} \times N_{y} \times N_{z}}

定义两个矩阵的点乘运算：

{(P ⊙ Q)}_{ijk} = p_{ijk} q_{ijk}

可得式(2.6)：

(2.6)

\{\begin{matrix} \frac{? Tc ⊙ {(e^{*})}^{H_{c} t}}{? t} = T g_{c} ⊙ {(e^{*})}^{H_{c} t} \\ \frac{? Tη ⊙ {(e^{*})}^{H_{η} t}}{? t} = T g_{η} ⊙ {(e^{*})}^{H_{η} t} \end{matrix}

式(2.6)两侧均对时间积分可得到如下公式：

\{\begin{matrix} \int_{t_{n}}^{t_{n + 1}} \frac{? Tc ⊙ {(e^{*})}^{H_{c} τ}}{? t} dτ = \int_{t_{n}}^{t_{n + 1}} T g_{c} ⊙ {(e^{*})}^{H_{c} τ} dτ \\ \int_{t_{n}}^{t_{n + 1}} \frac{? Tη ⊙ {(e^{*})}^{H_{η} τ}}{? t} dτ = \int_{t_{n}}^{t_{n + 1}} T g_{η} ⊙ {(e^{*})}^{H_{η} τ} dτ \end{matrix}

积分后,得到的场变量在第n+1时间步和第n时间步的迭代关系如式(2.7)所示。

(2.7)

\{\begin{matrix} c_{n + 1} = T^{- 1} (\begin{matrix} T c_{n} ⊙ {(e^{*})}^{{- H}_{c} Δt} + \\ \int_{0}^{Δt} T g_{c} (t_{n} + τ) ⊙ {(e^{*})}^{H_{c} (τ - Δt)} dτ \end{matrix}) \\ η_{n + 1} = T^{- 1} (\begin{matrix} T η_{n} ⊙ {(e^{*})}^{{- H}_{η} Δt} + \\ \int_{0}^{Δt} T g_{η} (t_{n} + τ) ⊙ {(e^{*})}^{H_{η} (τ - Δt)} dτ \end{matrix}) \end{matrix}

根据拉格朗日多项式近似估计式(2.7)中关于非线性项的积分,得到一阶紧致指数时间差分方法的求解格式(2.8)。

(2.8)

\{\begin{matrix} c_{n + 1} = T^{- 1} (T c_{n} ⊙ {(e^{*})}^{{- H}_{c} Δt} + T g_{c} (c_{n}, η_{n}) ⊙ S_{c}) \\ η_{n + 1} = T^{- 1} (T η_{n} ⊙ {(e^{*})}^{{- H}_{η} Δt} + T g_{η} (c_{n}, η_{n}) ⊙ S_{η}) \end{matrix}

其中,

\{\begin{matrix} S_{c} = {(s_{c}^{ijk})}_{N_{x} \times N_{y} \times N_{z}}, s_{c}^{ijk} = \frac{1}{h_{c}^{ijk}} (1 - e^{- h_{c}^{ijk} Δt}) \\ S_{η} = {(s_{η}^{ijk})}_{N_{x} \times N_{y} \times N_{z}}, s_{η}^{ijk} = \frac{1}{h_{η}^{ijk}} (1 - e^{- h_{η}^{ijk} Δt}) \end{matrix}

预估校正的紧致指数时间差分方法二阶求解格式如下：

(2.9)

\{\begin{matrix} \overset{?}{c_{n + 1}} = T^{- 1} (T c_{n} ⊙ {(e^{*})}^{{- H}_{c} Δt} + T g_{c} (c_{n}, η_{n}) ⊙ S_{c}) \\ \overset{?}{η_{n + 1}} = T^{- 1} (T η_{n} ⊙ {(e^{*})}^{{- H}_{η} Δt} + T g_{η} (c_{n}, η_{n}) ⊙ S_{η}) \\ c_{n + 1} = T^{- 1} (\begin{matrix} T c_{n} ⊙ {(e^{*})}^{{- H}_{c} Δt} + \frac{1}{2} T g_{c} (c_{n}, η_{n}) ⊙ S_{c} \\ + \frac{1}{2} T g_{c} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) ⊙ S_{c} \end{matrix}) \\ η_{n + 1} = T^{- 1} (\begin{matrix} T η_{n} ⊙ {(e^{*})}^{{- H}_{η} Δt} + \frac{1}{2} T g_{η} (c_{n}, η_{n}) ⊙ S_{η} \\ + \frac{1}{2} T g_{η} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) ⊙ S_{η} \end{matrix}) \end{matrix}

2.2 能量稳定的证明

下面证明2.1节中得到的含弹性应变能的各项异性相场模型的紧致指数时间差分方法一阶求解格式（2.8）和二阶求解格式（2.9）的能量稳定性。在证明过程中引用了如下引理：

Lemma 2.1 对于任意给定的

N_{x} \times N_{y} \times N_{z}

的三维矩阵f和g,有：

\sum_{Ω_{h}} Δ_{h} f ⊙ g = - \sum_{Ω_{h}} (?_{h} f) ⊙ (?_{h} g) = \sum_{Ω_{h}} f ⊙ Δ_{h} g

Lemma 2.2 对于任意给定的

N_{x} \times N_{y} \times N_{z}

的三维矩阵f和g, 如果

g_{ijk} > 0

,则：

\sum_{Ω_{h}} T^{- 1} [T (- Δ_{h} f) ⊙ g] ⊙ f > 0

Lemma 2.3 （Young's Inequality）

设

p, q, r \in [1, \infty]

,满足

\frac{1}{p} + \frac{1}{q} = 1 + \frac{1}{r}

,若

f \in L^{p}

g \in L^{q}

,则

(f*g) (x) \in L^{r}

,且有估计式：

{‖f*g‖}_{r} \leq {‖f‖}_{p} {‖g‖}_{q}

下面是含弹性应变能的各向异性耦合方程一阶指数时间差分方法能量稳定性定理：

Theorem 2.1 对于含弹性应变能的各向异性的Allen-Cahn方程和Cahn-Hilliard方程的耦合模型（1.6）,如果满足条件：

\{\begin{matrix} κ_{c} \geq \frac{1}{2} \max (\frac{?^{2} f_{local}}{?^{2} c} + \frac{?^{2} f_{local}}{? c ? η}) \\ κ_{η} \geq \frac{1}{2} \max (\frac{?^{2} f_{local}}{?^{2} η} + \frac{?^{2} f_{local}}{? c ? η}) \\ κ_{el} \geq \frac{1}{2} {‖B (n)‖}_{1} \max (|\frac{? θ (c)}{? c}|) \\ (Κ - Λ) 是正定的 \end{matrix}

则一阶紧致指数时间差分方法求解格式(2.8)满足能量下降准则。

Theorem 2.1的证明如下：

根据一阶紧致指数时间差分方法公式（2.8）,可以得到：

\{\begin{matrix} {Tc}_{n} = T c_{n + 1} ⊙ {(e^{*})}^{H_{c} Δt} - T g_{c} (c_{n}, η_{n}) ⊙ S_{c} ⊙ {(e^{*})}^{H_{c} Δt} \\ {Tη}_{n} = T η_{n + 1} ⊙ {(e^{*})}^{H_{η} Δt} - T g_{η} (c_{n}, η_{n}) ⊙ S_{η} ⊙ {(e^{*})}^{H_{η} Δt} \end{matrix}

在方程两侧加上：

\{\begin{matrix} - T c_{n + 1} \\ - T η_{n + 1} \end{matrix}

并将方程中的S替换后可以得到：

\{\begin{matrix} {- T (c_{n + 1} - c}_{n}) ⊙ r_{c} = T c_{n + 1} ⊙ H_{c} - T g_{c} (c_{n}, η_{n}) \\ - T (η_{n + 1} {- η}_{n}) ⊙ r_{η} = T η_{n + 1} ⊙ H_{c} - T g_{η} (c_{n}, η_{n}) \end{matrix}

其中,

\{\begin{matrix} r_{c} = \frac{H_{c}}{{(e^{*})}^{H_{c} Δt} - 1} \geq 0 \\ r_{η} = \frac{H_{η}}{{(e^{*})}^{H_{η} Δt} - 1} \geq 0 \end{matrix}

方程两侧进行逆变换可以得到：

\{\begin{matrix} - {\frac{1}{M} T}^{- 1} ({T (c_{n + 1} - c}_{n}) ⊙ r_{c}) \\ = α ?_{h}^{2} c_{n + 1} - (κ_{c} + κ_{el}) ?_{h} c_{n + 1} \\ - ?_{h} (f_{c} + f_{el}) + (κ_{c} + κ_{el}) ?_{h} c_{n} \\ - {\frac{1}{L} T}^{- 1} (T (η_{n + 1} {- η}_{n}) ⊙ r_{η}) \\ = - βΚ Δ_{h} η_{n + 1} + κ_{η} η_{n + 1} \\ + f_{η} - κ_{η} η_{n} + β ?_{h} ? (Κ - Λ) ?_{h} η_{n} \end{matrix}

令

?_{h} u = (c_{n} - c_{n + 1})

{u|}_{? Ω} = 0

方程两侧同时乘上：

\{\begin{matrix} ⊙ u \\ ⊙ (η_{n + 1} {- η}_{n}) \end{matrix}

并根据Lemma 2.1进行离散积分,将两个变量的方程合并整理后可得如下方程：

\begin{matrix} - \frac{1}{M} \sum_{Ω_{h}} T^{- 1} ({T (c_{n + 1} - c}_{n}) ⊙ r_{c}) ⊙ u \\ - \frac{1}{L} \sum_{Ω_{h}} T^{- 1} (T (η_{n + 1} {- η}_{n}) ⊙ r_{η}) ⊙ (η_{n + 1} {- η}_{n}) \\ = \frac{1}{2} α {‖?_{h} c_{n + 1}‖}^{2} - \frac{1}{2} α {‖?_{h} c_{n}‖}^{2} \\ + \frac{1}{2} α {‖?_{h} c_{n + 1} - ?_{h} c_{n}‖}^{2} - \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} η_{n}]}^{T} ⊙ Λ ?_{h} η_{n} \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} η_{n + 1}]}^{T} ⊙ Λ ?_{h} η_{n + 1} \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} (η_{n + 1} {- η}_{n})]}^{T} ⊙ Κ ?_{h} (η_{n + 1} {- η}_{n}) \\ + \sum_{Ω_{h}} κ_{c} {(c_{n + 1} - c_{n})}^{2} + \sum_{Ω_{h}} f_{c} ⊙ (c_{n + 1} - c_{n}) \\ + \sum_{Ω_{h}} κ_{η} {{(η}_{n + 1} - η_{n})}^{2} + \sum_{Ω_{h}} f_{η} ⊙ (η_{n + 1} {- η}_{n}) \\ + \sum_{Ω_{h}} κ_{el} {(c_{n + 1} - c_{n})}^{2} + \sum_{Ω_{h}} f_{η} ⊙ (η_{n + 1} {- η}_{n}) \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} (η_{n + 1} {- η}_{n})]}^{T} ⊙ (Κ - Λ) ?_{h} (η_{n + 1} {- η}_{n}) \end{matrix}

根据局部能量密度和弹性应变能的二阶泰勒展开,得到系统第n 个时间步和第n+1个时间步的能量差的式两种等价形式,式（2.10）和式（2.11）。

(2.10)

\begin{matrix} E_{h} (η_{n}, c_{n}) - E_{h} (η_{n + 1}, c_{n + 1}) \\ = \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} η_{n}]}^{T} ⊙ Λ ?_{h} η_{n} \\ - \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} η_{n + 1}]}^{T} ⊙ Λ ?_{h} η_{n + 1} \\ + \frac{1}{2} α {‖?_{h} c_{n}‖}^{2} - \frac{1}{2} α {‖?_{h} c_{n + 1}‖}^{2} + \sum_{Ω_{h}} [{F_{el} (c_{n}) - F}_{el} (c_{n + 1})] \\ + \sum_{Ω_{h}} [{f_{local} (η_{n}, c_{n}) - f}_{local} (η_{n + 1}, c_{n + 1})] \end{matrix}

(2.11)

\begin{matrix} E_{h} (η_{n}, c_{n}) - E_{h} (η_{n + 1}, c_{n + 1}) \\ = \frac{1}{M} \sum_{Ω_{h}} T^{- 1} (T ?_{h} u ⊙ r_{c}) ⊙ u \\ + \frac{1}{L} \sum_{Ω_{h}} T^{- 1} (T (η_{n + 1} {- η}_{n}) ⊙ r_{η}) ⊙ (η_{n + 1} {- η}_{n}) \\ + \frac{1}{2} α {‖?_{h} c_{n + 1} - ?_{h} c_{n}‖}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} (η_{n + 1} {- η}_{n})]}^{T} ⊙ Κ ?_{h} (η_{n + 1} {- η}_{n}) \\ + \sum_{Ω_{h}} (κ_{c} - \frac{1}{2} f_{cc} - \frac{1}{2} f_{cη}) {(c_{n + 1} - c_{n})}^{2} \\ + \sum_{Ω_{h}} (κ_{η} - \frac{1}{2} f_{ηη} - \frac{1}{2} f_{cη}) {{(η}_{n + 1} - η_{n})}^{2} \\ + \sum_{Ω_{h}} (κ_{el} - \frac{1}{2} \frac{? f_{el}}{? c}) {(c_{n + 1} - c_{n})}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} f_{cη} {((c_{n + 1} - c_{n}) - (η_{n + 1} - η_{n}))}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} (η_{n + 1} {- η}_{n})]}^{T} ⊙ (Κ - Λ) ?_{h} (η_{n + 1} {- η}_{n}) \end{matrix}

根据Lemma 2.2 可知,式（2.11）中：

\begin{matrix} \frac{1}{M} \sum_{Ω_{h}} T^{- 1} (T ({- ?}_{h} u) ⊙ r_{c}) ⊙ u \\ + \frac{1}{L} \sum_{Ω_{h}} T^{- 1} (T (η_{n + 1} {- η}_{n}) ⊙ r_{η}) ⊙ (η_{n + 1} {- η}_{n}) \\ > 0 \end{matrix}

根据Lemma 2.3可得：

\frac{? f_{el}}{? c} \leq {‖B (n)‖}_{1} \max (|\frac{? θ (c)}{? c}|)

因此,若满足Theorem2.1中描述的条件,则式（2.11）的右侧大于0,即：

E_{h} (η_{n}, c_{n}) - E_{h} (η_{n + 1}, c_{n + 1}) > 0

满足能量下降准则,Theorem 2.1得证。

下面是含弹性应变能的各向异性耦合方程二阶指数时间差分方法能量稳定性定理：

Theorem 2.2 对于含弹性应变能的各向异性的Allen-Cahn方程和Cahn-Hilliard方程的耦合模型（1.6）,如果满足条件

\{\begin{matrix} κ_{c} \geq \frac{1}{2} \max (\frac{?^{2} f_{local}}{?^{2} c} + \frac{?^{2} f_{local}}{? c ? η}) \\ κ_{η} \geq \frac{1}{2} \max (\frac{?^{2} f_{local}}{?^{2} η} + \frac{?^{2} f_{local}}{? c ? η}) \\ κ_{el} \geq \frac{1}{2} {‖B (n)‖}_{1} \max (|\frac{? θ (c)}{? c}|) \\ (Κ - Λ) 是正定的 \end{matrix}

则二阶紧致指数时间差分方法求解格式(2.9)满足能量下降准则。

Theorem 2.2的证明如下：

根据二阶紧致指数时间差分方法公式（2.9）可得：

\{\begin{matrix} - \frac{1}{2} T c_{n} = - T (c_{n + 1} - \frac{1}{2} \overset{?}{c_{n + 1}}) ⊙ {(e^{*})}^{H_{c} Δt} \\ + \frac{1}{2} T g_{c} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) ⊙ S_{c} ⊙ {(e^{*})}^{H_{c} Δt} \\ - \frac{1}{2} T η_{n} = - T (η_{n + 1} - \frac{1}{2} \overset{?}{η_{n + 1}}) ⊙ {(e^{*})}^{H_{c} Δt} \\ + \frac{1}{2} T g_{η} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) ⊙ S_{η} ⊙ {(e^{*})}^{H_{η} Δt} \end{matrix}

在方程两侧加上：

\{\begin{matrix} - T (c_{n + 1} - \frac{1}{2} \overset{?}{c_{n + 1}}) \\ - T (η_{n + 1} - \frac{1}{2} \overset{?}{η_{n + 1}}) \end{matrix}

并替换方程中的S可得：

\{\begin{matrix} - T (c_{n + 1} - \frac{1}{2} c_{n} - \frac{1}{2} \overset{?}{c_{n + 1}}) ⊙ r_{c} \\ = T (c_{n + 1} - \frac{1}{2} \overset{?}{c_{n + 1}}) ⊙ H_{c} - \frac{1}{2} T g_{c} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) \\ - T (η_{n + 1} - \frac{1}{2} η_{n} - \frac{1}{2} \overset{?}{η_{n + 1}}) ⊙ r_{η} \\ = T (η_{n + 1} - \frac{1}{2} \overset{?}{η_{n + 1}}) ⊙ H_{η} - \frac{1}{2} T g_{η} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) \end{matrix}

其中r的取值和Theorem 2.1的证明中相同。

方程两侧进行逆变换得到：

\{\begin{matrix} - \frac{1}{M} T^{- 1} [T (c_{n + 1} - \overset{?}{c_{n + 1}}) ⊙ r_{c}] \\ - \frac{1}{M} T^{- 1} [T (\frac{1}{2} \overset{?}{c_{n + 1}} - \frac{1}{2} c_{n}) ⊙ r_{c}] \\ = α ?_{h}^{2} (c_{n + 1} - \frac{1}{2} \overset{?}{c_{n + 1}}) \\ - (κ_{c} + κ_{el}) ?_{h} (c_{n + 1} - \frac{1}{2} \overset{?}{c_{n + 1}}) + \frac{1}{2} (κ_{c} + κ_{el}) ?_{h} \overset{?}{c_{n + 1}} \\ - \frac{1}{2} ?_{h} f_{c} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) - \frac{1}{2} ?_{h} f_{el} (\overset{?}{c_{n + 1}}) \\ - \frac{1}{L} T^{- 1} [T (η_{n + 1} - \overset{?}{η_{n + 1}}) ⊙ r_{η}] \\ - \frac{1}{L} T^{- 1} [T (\frac{1}{2} \overset{?}{η_{n + 1}} - \frac{1}{2} η_{n}) ⊙ r_{η}] \\ = - β Κ Δ_{h} (η_{n + 1} - \frac{1}{2} \overset{?}{η_{n + 1}}) + κ_{η} (η_{n + 1} - \frac{1}{2} \overset{?}{η_{n + 1}}) \\ + \frac{1}{2} f_{η} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) - \frac{1}{2} κ_{η} \overset{?}{η_{n + 1}} + \frac{1}{2} β ?_{h} ? (Κ - Λ) ?_{h} \overset{?}{η_{n + 1}} \end{matrix}

令

?_{h} w = (\overset{?}{c_{n + 1}} - c_{n + 1})

,且

{w|}_{? Ω} = 0

,

方程两侧乘

\{\begin{matrix} ⊙ w \\ ⊙ (η_{n + 1} - \overset{?}{η_{n + 1}}) \end{matrix}

根据Lemma 2.1 进行离散积分,并根据Theorem 2.1的证明可得如下等式：

\begin{matrix} f_{1} = \frac{1}{4} α {‖?_{h} c_{n + 1}‖}^{2} - \frac{1}{4} α {‖?_{h} c_{n}‖}^{2} \\ + \frac{1}{4} α {‖?_{h} \overset{?}{c_{n + 1}} - ?_{h} c_{n}‖}^{2} + \frac{3}{4} α {‖?_{h} (c_{n + 1} - \overset{?}{c_{n + 1}})‖}^{2} \\ + \frac{1}{4} β \sum_{Ω_{h}} {[?_{h} η_{n + 1}]}^{T} ⊙ {Λ ?}_{h} η_{n + 1} \\ + \frac{3}{4} \sum_{Ω_{h}} β {[?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}})]}^{T} ⊙ Κ ?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}}) \\ - \frac{1}{4} \sum_{Ω_{h}} β {[?_{h} η_{n}]}^{T} ⊙ Λ ?_{h} η_{n} \\ + \frac{1}{4} \sum_{Ω_{h}} β {[?_{h} (\overset{?}{η_{n + 1}} {- η}_{n})]}^{T} ⊙ Κ ?_{h} (\overset{?}{η_{n + 1}} {- η}_{n}) \\ + \frac{1}{4} \sum_{Ω_{h}} \begin{matrix} β {[?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}})]}^{T} \\ ⊙ (Κ - Λ) ?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}}) \end{matrix} \\ + \frac{1}{4} \sum_{Ω_{h}} β {[?_{h} (\overset{?}{η_{n + 1}} {- η}_{n})]}^{T} (Κ - Λ) ⊙ ?_{h} (\overset{?}{η_{n + 1}} {- η}_{n}) \\ + \sum_{Ω_{h}} κ_{c} {({\overset{?}{c_{n + 1}} - c}_{n + 1})}^{2} + \frac{1}{2} \sum_{Ω_{h}} κ_{c} {(\overset{?}{c_{n + 1}} - c_{n})}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} f_{c} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) ⊙ (c_{n + 1} - \overset{?}{c_{n + 1}}) \\ + \frac{1}{2} \sum_{Ω_{h}} f_{c} (c_{n}, η_{n}) ⊙ (\overset{?}{c_{n + 1}} - c_{n}) \\ + \sum_{Ω_{h}} κ_{el} {({\overset{?}{c_{n + 1}} - c}_{n + 1})}^{2} + \frac{1}{2} \sum_{Ω_{h}} κ_{el} {(\overset{?}{c_{n + 1}} - c_{n})}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} f_{el} (\overset{?}{c_{n + 1}}) ⊙ (c_{n + 1} - \overset{?}{c_{n + 1}}) \\ + \frac{1}{2} \sum_{Ω_{h}} f_{el} (c_{n}) ⊙ (\overset{?}{c_{n + 1}} - c_{n}) \\ + \sum_{Ω_{h}} κ_{η} {(η_{n + 1} - \overset{?}{η_{n + 1}})}^{2} + \frac{1}{2} \sum_{Ω_{h}} κ_{η} ({\overset{?}{η_{n + 1}} - η_{n})}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} f_{η} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) ⊙ (η_{n + 1} - \overset{?}{η_{n + 1}}) \\ + \frac{1}{2} \sum_{Ω_{h}} f_{η} (c_{n}, η_{n}) ⊙ (\overset{?}{η_{n + 1}} {- η}_{n}) \end{matrix}

其中,

(2.12)

\begin{matrix} f_{1} = - \frac{1}{M} \sum_{Ω_{h}} T^{- 1} [T (c_{n + 1} - \overset{?}{c_{n + 1}}) ⊙ r_{c}] ⊙ w \\ - \frac{1}{M} \sum_{Ω_{h}} T^{- 1} [T (\frac{1}{2} \overset{?}{c_{n + 1}} - \frac{1}{2} c_{n}) ⊙ r_{c}] ⊙ w \\ - \frac{1}{M} \sum_{Ω_{h}} T^{- 1} ({T (\overset{?}{c_{n + 1}} - c}_{n}) ⊙ \frac{1}{2} r_{c}) ⊙ u \\ - \frac{1}{L} \sum_{Ω_{h}} T^{- 1} (T (\overset{?}{η_{n + 1}} {- η}_{n}) ⊙ \frac{1}{2} r_{η}) ⊙ (\overset{?}{η_{n + 1}} {- η}_{n}) \\ - \frac{1}{L} \sum_{Ω_{h}} \begin{matrix} T^{- 1} [T (\frac{1}{2} \overset{?}{η_{n + 1}} - \frac{1}{2} η_{n}) ⊙ r_{η}] \\ ⊙ (η_{n + 1} - \overset{?}{η_{n + 1}}) \end{matrix} \\ - \frac{1}{L} \sum_{Ω_{h}} \begin{matrix} T^{- 1} [T (η_{n + 1} - \overset{?}{η_{n + 1}}) ⊙ r_{η}] \\ ⊙ (η_{n + 1} - \overset{?}{η_{n + 1}}) \end{matrix} \end{matrix}

将式中的局部能量密度和弹性应变能进行二阶泰勒展开,整理后得到系统第n个时间步和第n+1个时间步的能量之差的两种等价形式,如式（2.13）和式（2.14）所示：

(2.13)

\begin{matrix} E_{h} (η_{n}, c_{n}) - E_{h} (η_{n + 1}, c_{n + 1}) \\ = \frac{1}{2} α {‖?_{h} c_{n}‖}^{2} - \frac{1}{2} α {‖?_{h} c_{n + 1}‖}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} η_{n}]}^{T} ⊙ Λ ?_{h} η_{n} \\ - \frac{1}{2} β \sum_{Ω_{h}} {[?_{h} η_{n + 1}]}^{T} ⊙ {Λ ?}_{h} η_{n + 1} \\ + \sum_{Ω_{h}} [f_{local} (η_{n}, c_{n}) - f_{local} (η_{n + 1}, c_{n + 1})] \\ + \sum_{Ω_{h}} [F_{el} (c_{n}) - F_{el} (c_{n + 1})] \end{matrix}

(2.14)

\begin{matrix} E_{h} (η_{n}, c_{n}) - E_{h} (η_{n + 1}, c_{n + 1}) \\ = - 2 f_{1} \\ + \frac{1}{2} α {‖?_{h} \overset{?}{c_{n + 1}} - ?_{h} c_{n}‖}^{2} + \frac{3}{2} α {‖?_{h} (c_{n + 1} - \overset{?}{c_{n + 1}})‖}^{2} \\ + \frac{3}{2} \sum_{Ω_{h}} β {[?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}})]}^{T} ⊙ Κ ?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}}) \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} (\overset{?}{η_{n + 1}} {- η}_{n})]}^{T} ⊙ Κ ?_{h} (\overset{?}{η_{n + 1}} {- η}_{n}) \\ + \frac{1}{2} \sum_{Ω_{h}} [\begin{matrix} β {[?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}})]}^{T} ⊙ (Κ - Λ) ?_{h} (η_{n + 1} - \overset{?}{η_{n + 1}}) \end{matrix}] \\ + \frac{1}{2} \sum_{Ω_{h}} β {[?_{h} (\overset{?}{η_{n + 1}} {- η}_{n})]}^{T} (Κ - Λ) ⊙ ?_{h} (\overset{?}{η_{n + 1}} {- η}_{n}) \\ + 2 \sum_{Ω_{h}} (κ_{η} - \frac{1}{4} f_{ηη} (\overset{?}{η_{n + 1}}, \overset{?}{c_{n + 1}}) - \frac{1}{4} f_{cη} (\overset{?}{η_{n + 1}}, \overset{?}{c_{n + 1}})) {(\overset{?}{η_{n + 1}} - η_{n + 1})}^{2} \\ + 2 \sum_{Ω_{h}} (κ_{c} - \frac{1}{4} f_{cc} (\overset{?}{η_{n + 1}}, \overset{?}{c_{n + 1}}) - \frac{1}{4} f_{cη} (\overset{?}{η_{n + 1}}, \overset{?}{c_{n + 1}})) {({\overset{?}{c_{n + 1}} - c}_{n + 1})}^{2} \\ + \sum_{Ω_{h}} (κ_{η} - \frac{1}{2} f_{ηη} - \frac{1}{2} f_{cη}) ({\overset{?}{η_{n + 1}} - η_{n})}^{2} \\ + \sum_{Ω_{h}} (κ_{c} - \frac{1}{2} f_{cc} - \frac{1}{2} f_{cη}) {(\overset{?}{c_{n + 1}} - c_{n})}^{2} \\ + \sum_{Ω_{h}} (κ_{el} - \frac{1}{2} \frac{? f_{el}}{? c}) {(\overset{?}{c_{n + 1}} - c_{n})}^{2} \\ + 2 \sum_{Ω_{h}} (κ_{el} - \frac{1}{4} \frac{? f_{el} (\overset{?}{η_{n + 1}}, \overset{?}{c_{n + 1}})}{? c}) {({\overset{?}{c_{n + 1}} - c}_{n + 1})}^{2} \\ + \frac{1}{2} \sum_{Ω_{h}} [\begin{matrix} {f_{cη} (\overset{?}{η_{n + 1}}, \overset{?}{c_{n + 1}}) ⊙ [(c_{n + 1} - \overset{?}{c_{n + 1}}) - (η_{n + 1} - \overset{?}{η_{n + 1}})]}^{2} \end{matrix}] \\ + \frac{1}{2} \sum_{Ω_{h}} f_{cη} {[(\overset{?}{c_{n + 1}} - c_{n}) - (\overset{?}{η_{n + 1}} - η_{n})]}^{2} \end{matrix}

根据Lemma 2.2 可知,式（2.12）和式（2.14）中：

f_{1} < 0

根据Lemma 2.3可得：

\frac{? f_{el}}{? c} \leq {‖B (n)‖}_{1} \max (|\frac{? θ (c)}{? c}|)

因此,若满足Theorem2.2中描述的条件,则式（2.14）的右侧大于0,即：

E_{h} (η_{n}, c_{n}) - E_{h} (η_{n + 1}, c_{n + 1}) > 0

满足能量下降准则,Theorem 2.2得证。

2.3 指数时间差分方法的时间精度

下面通过局部截断误差分析指数时间差分方法一阶和二阶求解格式的精度。

为了求解第n个时间步与第n+1个时间步的局部截断误差,首先假设第n个时间步的数值解与精确解相等：

\{\begin{matrix} c (t_{n}) = c_{n} \\ η (t_{n}) = η_{n} \end{matrix}

一阶求解格式的局部截断误差定义为：

\{\begin{matrix} T_{c}^{1} = c (t_{n + 1}) - c_{n + 1} \\ T_{η}^{1} = η (t_{n + 1}) - η_{n + 1} \end{matrix}

将一阶求解格式的数值解式(2.8)与精确解（2.7）作差并将积分展开可得：

\{\begin{matrix} c_{n + 1} - c (t_{n + 1}) \\ = T^{- 1} (\begin{matrix} T (g_{c} (c_{n - 1}, η_{n - 1}) - g_{c} (c_{n}, η_{n})) ⊙ (\frac{1}{h_{c}^{ijk}} (1 - \frac{1}{? t} S_{c})) \end{matrix}) \\ η_{n + 1} - η (t_{n + 1}) \\ = T^{- 1} (\begin{matrix} T (g_{η} (c_{n - 1}, η_{n - 1}) - g_{η} (c_{n}, η_{n})) ⊙ (\frac{1}{h_{η}^{ijk}} (1 - \frac{1}{? t} S_{η})) \end{matrix}) \end{matrix}

将S代入并进行泰勒展开可得：

(2.15)

\{\begin{matrix} c_{n + 1} - c (t_{n + 1}) = T^{- 1} (\begin{matrix} T (g_{c} (c_{n}, η_{n}) - g_{c} (c_{n - 1}, η_{n - 1})) \\ ⊙ (\frac{1}{2} ? t - \frac{1}{6} h_{c}^{ijk} {? t}^{2} + o ({? t}^{3})) \end{matrix}) \\ η_{n + 1} - η (t_{n + 1}) = T^{- 1} (\begin{matrix} T ({g_{η} (c_{n}, η_{n}) - g}_{η} (c_{n - 1}, η_{n - 1})) \\ ⊙ (\frac{1}{2} ? t - \frac{1}{6} h_{c}^{ijk} {? t}^{2} + o ({? t}^{3})) \end{matrix}) \end{matrix}

因此,局部截断误差为：

\{\begin{matrix} T_{c}^{1} = - \frac{1}{2} \frac{d g_{c} (c_{n}, η_{n})}{dt} {? t}^{2} + o ({? t}^{3}) \\ T_{η}^{1} = - \frac{1}{2} \frac{d g_{η} (c_{n}, η_{n})}{dt} {? t}^{2} + o ({? t}^{3}) \end{matrix}

将g代入得到：

\{\begin{matrix} T_{c}^{1} = - \frac{1}{2} M \frac{d ?_{h} (f_{c} + f_{el})}{dt} {? t}^{2} \\ + \frac{1}{2} M (κ_{c} + κ_{el}) \frac{d ?_{h} c}{dt} {? t}^{2} + o ({? t}^{3}) \\ T_{η}^{1} = \frac{1}{2} L \frac{d f_{η}}{dt} {? t}^{2} \\ - L \frac{d (κ_{η} η - β ?_{h} ? (Κ - Λ) ?_{h} η)}{dt} {? t}^{2} + o ({? t}^{3}) \end{matrix}

指数时间差分方法一阶求解格式的局部截断误差的主项为二阶,因此该格式的时间精度为一阶。

二阶求解格式的局部截断误差定义为：

\{\begin{matrix} T_{c}^{2} = c (t_{n + 1}) - c_{n + 1} \\ T_{η}^{2} = η (t_{n + 1}) - η_{n + 1} \end{matrix}

将二阶求解格式（2.9）中的预估与校正公式作差可得：

(2.16)

\{\begin{matrix} c_{n + 1} - \overset{?}{c_{n + 1}} = T^{- 1} (\begin{matrix} T (g_{c} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) - g_{c} (c_{n}, η_{n})) \\ ⊙ (\frac{1}{2} ? t - \frac{1}{4} h_{c}^{ijk} {? t}^{2} + o ({? t}^{3})) \end{matrix}) \\ η_{n + 1} - \overset{?}{η_{n + 1}} = T^{- 1} (\begin{matrix} T ({g_{η} (\overset{?}{c_{n + 1}}, \overset{?}{η_{n + 1}}) - g}_{η} (c_{n}, η_{n})) \\ ⊙ (\frac{1}{2} ? t - \frac{1}{4} h_{c}^{ijk} {? t}^{2} + o ({? t}^{3})) \end{matrix}) \end{matrix}

根据式（2.15）可得预估步与精确解的差值：

(2.17)

\{\begin{matrix} \overset{?}{c_{n + 1}} - c (t_{n + 1}) = T^{- 1} (\begin{matrix} T (g_{c} (c_{n}, η_{n}) - g_{c} (c_{n - 1}, η_{n - 1})) \\ ⊙ (\frac{1}{2} ? t - \frac{1}{6} h_{c}^{ijk} {? t}^{2} + o ({? t}^{3})) \end{matrix}) \\ \overset{?}{η_{n + 1}} - η (t_{n + 1}) = T^{- 1} (\begin{matrix} T ({g_{η} (c_{n}, η_{n}) - g}_{η} (c_{n - 1}, η_{n - 1})) \\ ⊙ (\frac{1}{2} ? t - \frac{1}{6} h_{c}^{ijk} {? t}^{2} + o ({? t}^{3})) \end{matrix}) \end{matrix}

将式（2.16）与式（2.17）相加并整理可得,二阶格式的局部截断误差为：

\{\begin{matrix} T_{c}^{2} = - \frac{1}{2} \frac{d^{2} g_{c} (c_{n}, η_{n})}{d^{2} t} {? t}^{3} + \frac{5}{12} \frac{d g_{c} (c_{n}, η_{n})}{dt} {⊙ h}_{c}^{ijk} {? t}^{3} + o ({? t}^{4}) \\ T_{η}^{2} = - \frac{1}{2} \frac{d^{2} g_{η} (c_{n}, η_{n})}{d^{2} t} {? t}^{3} + \frac{5}{12} \frac{d g_{η} (c_{n}, η_{n})}{dt} {⊙ h}_{c}^{ijk} {? t}^{3} + o ({? t}^{4}) \end{matrix}

将g 和h代入公式可得：

\{\begin{matrix} T_{c}^{2} = \frac{5}{12} M^{2} (κ_{c} + κ_{el}) (d_{x}^{i} + d_{y}^{j} + d_{z}^{k}) \\ \frac{d [\begin{matrix} ((κ_{c} + κ_{el}) - α (d_{x}^{i} + d_{y}^{j} + d_{z}^{k})) ?_{h} c {- ?}_{h} (f_{c} + f_{el}) \end{matrix}]}{dt} {? t}^{3} \\ + \frac{5}{12} M^{2} α {(d_{x}^{i} + d_{y}^{j} + d_{z}^{k})}^{2} \frac{d ?_{h} (f_{c} + f_{el})}{dt} {? t}^{3} \\ + \frac{1}{2} M (κ_{c} + κ_{el}) \frac{d^{2} ?_{h} c}{d^{2} t} {? t}^{3} - \frac{1}{2} M \frac{d^{2} ?_{h} (f_{c} + f_{el})}{d^{2} t} {? t}^{3} + o ({? t}^{4}) \\ T_{η}^{2} = \frac{5}{12} L^{2} (β (k_{x} d_{x}^{i} + k_{y} d_{y}^{j} + k_{z} d_{z}^{k}) - κ_{η}) \\ \frac{d [f_{η} - κ_{η} η + β ?_{h} ? (Κ - Λ) ?_{h} η]}{dt} {? t}^{3} \\ + \frac{1}{2} L \frac{d^{2} [β ?_{h} ? K ?_{h} η - κ_{η} η]}{d^{2} t} + \frac{1}{2} L \frac{d^{2} [f_{η} - β ?_{h} ? Λ ?_{h} η]}{d^{2} t} {? t}^{3} + o ({? t}^{4}) \end{matrix}

指数时间差分方法二阶求解格式的局部截断误差主项为三阶,因此该格式的时间精度为二阶。

3 数值实验

通过观察镍基合金数值实验和Zr的氢化物堆叠数值实验两个相场模型的数值模拟结果,对含有界面能各向异性和弹性应变能的紧致指数时间差分方法的正确性以及算子分裂格式的能量稳定性进行验证。本文中的数值实验是在中国科学院计算机网络信息中心的超级计算机“元”二期计算系统的 CPU 节点进行。以下数值实验均为三维模拟,为方便观察,实验结果为模拟区域中心截面截图。

3.1 镍基合金的数值实验

镍基合金的数值实验^[13]模拟了高温下的单一无序相分解成低温下的富溶质的有序相和溶质贫化的无序相的过程。该数值实验的相场模型不含界面能各向异性,因此我们关注的重点是弹性应变能的作用。其相场耦合方程如式(3.1)所示。

(3.1)

\{\begin{matrix} \frac{? c}{? t} = M (- α ?^{2} c + ? (f_{c} + f_{el})) \\ \frac{? η}{? t} = L (β ? η - f_{η}) \end{matrix}

其中,

\{\begin{matrix} f_{c} = \frac{? f_{local} (c, η)}{? c} = A_{1} (c - C_{1}) - 0.5 A_{2} η^{2} \\ f_{η} = \frac{? f_{local} (c, η)}{? η} = A_{2} (C_{2} - c) η - A_{3} η^{3} + A_{4} η^{5} \end{matrix}

f_{el} = \frac{δ E_{el}}{δc} = {\{B (n) {\{θ (c)\}}_{k}\}}_{r}

数值实验中的参数均采用无量纲化后的取值。其中,

A_{1} = 62.5

A_{2} = 25

A_{3} = 12

A_{4} = 6.25

C^{'} = 0.2

C^{''} = 0.6

,迁移率M为1.0,扩散系数L为1.0,界面梯度能量的系数的取值为：

α = β = 6.25

弹性应变能计算相关的弹性应变矩阵和刚度矩阵如下：

C_{ijkl} = [\begin{matrix} \begin{matrix} 223 & 148 & 148 \\ 148 & 223 & 148 \\ 148 & 148 & 224 \end{matrix} & 0 \\ 0 & \begin{matrix} 125 \\ 125 \\ 125 \end{matrix} \end{matrix}]

ε^{0} = [\begin{matrix} 0.0079 \\ 0.0079 \\ 0.0079 \end{matrix}]

模拟的时间步长为1e-2,模拟的总时间为20.0,网格尺寸为1.0,三维的模拟区域大小为

128 \times 128 \times 128

。在模拟的初始状态,模拟区域中央给定一个半径为8个网格宽度的新相粒子,场变量c的初始值为0.4和0.65,场变量

η

的取值为0和1.4。^[14]算子分裂参数取值如下：

\{\begin{matrix} κ_{η} = 27 \\ κ_{c} = 35 \\ κ_{el} = 30 \end{matrix}

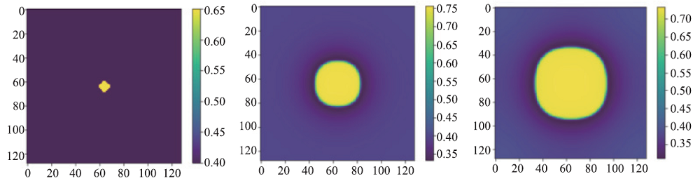
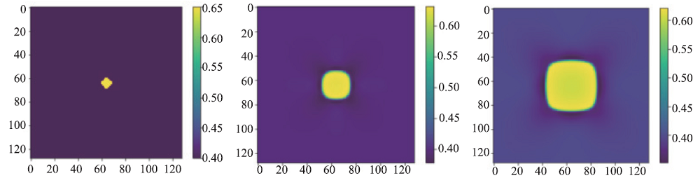
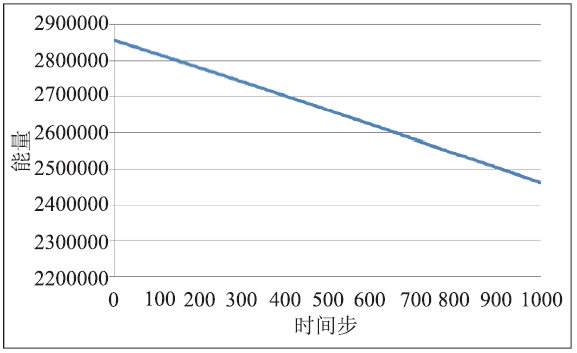
以下分别进行了无弹性应变能和有弹性应变能的模拟。无弹性应变能的场变量c在迭代步数t=0,1000,2000的模拟结果如（图1）所示,没有弹性应变能的作用,粒子随着时间生长,演化成了球形;有弹性应变能的场变量c在迭代步数 t=0,1000,2000的模拟结果如（图2）所示。在弹性应变能的作用下,粒子随时间生长,演化成了方形。其能量下降曲线如（图3）所示,能量稳定。

图1

新窗口打开|下载原图ZIP|生成PPT
图1不含弹性应变能的镍基合金数值实验的模拟结果

Fig.1Simulation results of numerical experiment of Ni-based alloy without elastic strain energy

图2

新窗口打开|下载原图ZIP|生成PPT
图2含有弹性应变能的镍基合金数值实验模拟结果

Fig.2Simulation results of numerical experiment of Ni-based alloy with elastic strain energy

图3

新窗口打开|下载原图ZIP|生成PPT
图3镍基合金数值实验的能量下降曲线

Fig.3Energy decline curve of numerical experiment of Ni-based alloy

3.2 Zr的氢化物堆叠数值实验

Zr的氢化物堆叠数值实验^[8]是描述氢化物在Zr中的堆积结构形成和转变的三维相场模型。该数值实验既含有界面能各向异性,又含有弹性应变能。其耦合方程如式(3.2)所示：

(3.2)

\{\begin{matrix} \frac{? c}{? t} = D (? c + f_{c}) \\ \frac{? η}{? t} = - M (- {k_{η}}^{2} ? ? Λ ? η + f_{η} + f_{el}) \end{matrix}

其中,

\{\begin{matrix} f_{c} = ? ? ((c_{α} - c_{δ}) \frac{? h (η)}{? η}) ? η \\ f_{η} = - \frac{? h (η)}{? η} f^{α} (c_{α}) + \frac{? f^{α} (c_{α})}{? η} (1 - h (η)) \\ + \frac{? h (η)}{? η} f^{δ} (c_{δ}) + \frac{? f^{δ} (c_{δ})}{? η} h (η) + w \frac{? g (η)}{? η} \end{matrix}

\{\begin{matrix} h (η) = 3 η^{2} - 2 η^{3} \\ g (η) = η^{2} - 2 η^{3} + η^{4} \end{matrix}

f_{el} = \frac{δ E_{el}}{δη} = {\{B (n) {\{θ (η)\}}_{k}\}}_{r}

w为1.848e9,迁移率M为5e-4,扩散系数D为1.2302e-10,界面梯度能量的系数的取值为：

{k_{η}}^{2} = 0.5318 e - 9

界面能各向异性矩阵取值如下：

Λ = [\begin{matrix} 1.0 \\ 1.0 \\ 0.005 \end{matrix}]

弹性应变能计算相关的弹性应变矩阵和刚度矩阵为：

C_{ijkl} = [\begin{matrix} \begin{matrix} 155 & 67 & 65 \\ 67 & 155 & 65 \\ 65 & 65 & 173 \end{matrix} & 0 \\ 0 & \begin{matrix} 40 \\ 40 \\ 44 \end{matrix} \end{matrix}]

ε^{0} = [\begin{matrix} 0.0457 & 0 & 0 \\ 0 & 0.0457 & 0.1943 \\ 0 & 0.1943 & 0.0721 \end{matrix}]

模拟的时间步长为1e-7,模拟的总时间为2e-4,网格尺寸为1e-9,三维的模拟区域大小为

128 \times 128 \times 128

。在模拟的初始状态,模拟区域中央给定一个半径为10个网格宽度的新相粒子,场变量c的初始值为0.1和0.5982,场变量

η

的取值为0和1.0。

紧致指数时间差分方法算子分裂参数取值为：

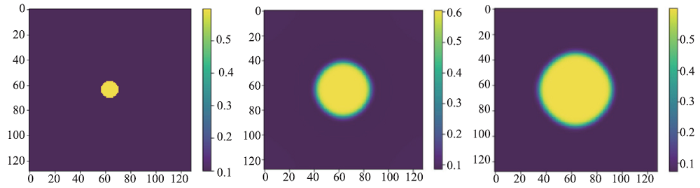
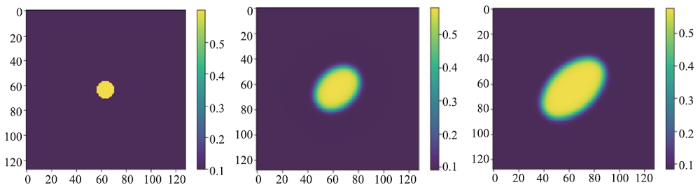
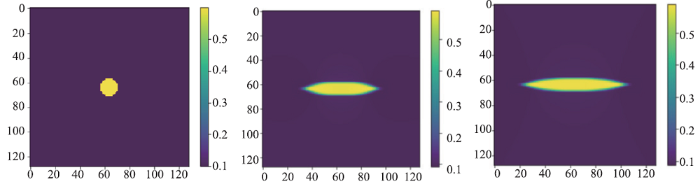
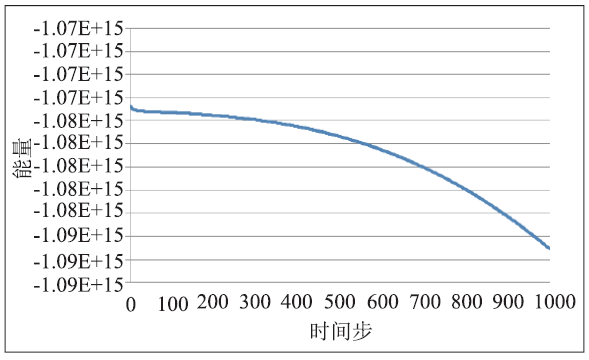
\{\begin{matrix} κ_{η} = 5 e 9 \\ κ_{c} = 1 e 17 \\ κ_{el} = 1 e 9 \end{matrix}

K = [\begin{matrix} 1.0 \\ 1.0 \\ 1.0 \end{matrix}]

下面分别进行了有无界面能各向异性和有无弹性应变能的四组数值实验。无界面能各向异性和弹性应变能,模拟结果如（图4）所示,氢化物逐渐演化为球体;有弹性应变能,无界面能各向异性,如（图5）所示,氢化物发生旋转,成为椭球体;无弹性应变能,有界面能各向异性,模拟结果如（图6）所示,氢化物在界面能各向异性的作用下变成圆盘;有弹性应变能和界面能各向异性,模拟结果如（图7）所示,氢化物在界面能各向异性的作用下变成圆盘,在弹性应变能的作用下发生旋转,但是在两者的共同作用下,氢化物旋转的角度小于只有弹性应变能作用的情况下的旋转角度。其能量下降曲线如（图8）所示,能量稳定。

图4

新窗口打开|下载原图ZIP|生成PPT
图4无界面能各向异性、无弹性应变能的Zr的氢化物数值实验的演化过程

Fig.4Evolution process of numerical experiment of Zr-hydride without interface energy anisotropy and elastic strain energy

图5

新窗口打开|下载原图ZIP|生成PPT
图5无界面能各向异性、有弹性应变能的Zr的氢化物数值实验的演化过程

Fig.5Evolution process of numerical experiment of Zr-hydride without interface energy anisotropy and with elastic strain energy

图6

新窗口打开|下载原图ZIP|生成PPT
图6有界面能各向异性、无弹性应变能的Zr的氢化物数值实验的演化过程

Fig.6Evolution process of numerical experiment of Zr-hydride with interface energy anisotropy and without elastic strain energy

图7

新窗口打开|下载原图ZIP|生成PPT
图7有界面能各向异性,有弹性应变能的Zr的氢化物数值实验的演化过程

Fig.7Evolution process of numerical experiment of Zr- hydride with interface energy anisotropy and elastic strain energy

图8

新窗口打开|下载原图ZIP|生成PPT
图8Zr的氢化物数值实验的能量下降曲线

Fig.8Energy decline curve of numerical experiment of Zr-hydride

下面进行了一系列时间步长倍增的实验用以验证指数时间差分方法的时间精度。时间步长分别取dt=

δ

\sqrt 2 δ

2 δ

2 \sqrt 2 δ

4 δ

（其中

δ

=4e-9）,以相同初始值运行至同一时刻T=2.56e-5,将时间步长dt=1e-9作为基准解。计算了指数时间差分方法一阶格式的

L^{2}

误差和收敛率如表1所示,收敛率的值接近1;二阶格式的

L^{2}

误差和收敛率如表2所示,收敛率的值接近2,验证了求解格式的时间精度。

Table 1
表1
表1指数时间差分方法一阶求解格式的误差
Table 1The error of the first order scheme of the Exponential Time Difference method

时间步长	$δ$	$\sqrt 2 δ$	$2 δ$	$2 \sqrt 2 δ$	$4 δ$
$\eta $的 $L^{2}$ 误差	7.31E-02	1.07E-01	1.67E-01	2.70E-01	4.30E-01
$\eta $的收敛率	1.11	1.28	1.39	1.34	-
c的 $L^{2}$ 误差	5.05E-02	7.00E-02	1.08E-01	1.72E-01	2.71E-01
c的收敛率	0.95	1.25	1.34	1.31	-

新窗口打开|下载CSV

表2
表2指数时间差分方法二阶求解格式的误差
The error of the second order scheme of the Exponential Time Difference method

时间步长	$δ$	$\sqrt 2 δ$	$2 δ$	$2 \sqrt 2 δ$	$4 δ$
$\eta $的 $L^{2}$ 误差	4.36E-03	7.49E-03	1.46E-02	3.39E-02	6.51E-02
$\eta $的收敛率	1.56	1.93	2.43	1.88	-
c的 $L^{2}$ 误差	2.39E-03	4.11E-03	8.10E-03	1.94E-02	3.81E-02
c的收敛率	1.56	1.96	2.52	1.94	-

新窗口打开|下载CSV

4 结论与展望

本文在紧致指数时间差分方法框架下引入了界面能各向异性和弹性应变能的计算,将界面能各向异性和弹性应变能归于紧致指数时间差分方法的非线性项统一处理,通过积分和预估校正的二阶近似进行计算,为保证能量稳定,设计了界面能各向异性和弹性应变能的算子分裂格式,并对算子分裂格式的能量稳定性进行了数学证明。通过材料腐蚀相场模型的数值实验,观察了界面能各向异性和弹性应变能对场变量演化的影响,验证了含弹性应变能的各向异性相场模型的指数时间差分方法算子分裂格式的能量稳定性。本文使用超级计算系统“元”对指数时间差分方法的格式精度和能量稳定性进行了验证,在后续的工作中,拟使用“天河二号”超级计算机进行并行扩展性的测试。^[15,16]本文仅得到了指数时间差分方法的一阶和二阶求解格式,更高阶的求解格式及其稳定性有待进一步探索。

利益冲突声明

所有作者声明不存在利益冲突关系。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Chen L

. Phase-field models for microstructure evolution
[J]. Annual review of materials research, 2002,32(1):113-140.

[本文引用: 1]

[2]

Allen S

, Cahn J

. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening
[J]. Acta Metallurgica, 1979,27(6):1085-1095.

[本文引用: 1]

[3]

Cahn J

, Hilliard J

. Free energy of a nonuniform system. I. Interfacial free energy
[J]. The Journal of chemical physics, 1958,28(2):258-267.

[本文引用: 1]

[4]

Kassam A

, Trefethen L

. Fourth-order time-stepping for stiff PDEs
[J]. SIAM Journal on Scientific Computing, 2005,26(4):1214-1233.

[本文引用: 1]

[5]

Kobayashi

. Modeling and numerical simulations of dendritic crystal growth
[J]. Physica D Nonlinear Phenomena, 1993,63(3-4):410-423.[Computation of dendrites using a phase field model].

DOI:10.1016/0167-2789(93)90120-P URL [本文引用: 1]

[6]

Kostorz

. Theory of structural transformations in solids by A. G. Khachaturyan
[J]. Acta Crystallographica Section A, 1985,41(2):208-208.

[本文引用: 1]

[7]

Tang

, Cui Y

, Chang

, et al. A phase-field approach to athermal β→ω transformation
[J]. Computational materials science, 2012,53(1):187-193.

DOI:10.1016/j.commatsci.2011.09.011 URL [本文引用: 1]

A quantitative phase-field model has been developed to simulate the microstructural evolution during the athermal beta -> omega transformation in the Zr-Nb alloys by incorporating to a CALPHAD-based thermodynamic description. While reflecting the essential physics of collapse mechanism that leads to displacive beta -> omega transformation, the simulations appropriately predicted the morphology and orientation of the athermal x phase upon different quenching processes, and the selective growth of the x phase subjected to various applied stresses, which are generally hard to observe experimentally. (C) 2011 Elsevier B. V.

[8]

Han G

, Zhao Y

, Zhou C

, et al. Phase-field modeling of stacking structure formation and transition of δ-hydride precipitates in zirconium
[J]. Acta Materialia, 2019,165:528-546.

[本文引用: 2]

[9]

, Zhang

, Zhu

, et al. Fast Explicit Integration Factor Methods for Semilinear Parabolic Equations
[J]. Journal of Scientific Computing, 2015,62(2):431-455.

DOI:10.1007/s10915-014-9862-9 URL [本文引用: 3]

[10]

, Zhang

, Du

. Fast and accurate algorithms for simulating coarsening dynamics of Cahn-Hilliard equations
[J]. Computational Materials Science, 2015,108:272-282.

DOI:10.1016/j.commatsci.2015.04.046 URL [本文引用: 1]

[11]

尹吉宪, 张鉴. 相场方程指数时间差分方法的能量稳定性分析
[J]. 科研信息化技术与应用, 2019,10(1):20-30.

[本文引用: 1]

[12]

Van Loan

. Computational frameworks for the fast Fourier transform
[M]. Siam, 1992.

[本文引用: 1]

[13]

Wang

, Khachaturyan A

. Shape instability during precipitate growth in coherent solids
[J]. Acta Metallurgica Et Materialia, 1995,43(5):1837-1857.

DOI:10.1016/0956-7151(94)00406-8 URL [本文引用: 1]

[14]

迟学斌, 赵莲, 王姗姗, 张鉴, 姜金荣. 高性能计算框架软件——SC_Tangram
[J]. 数据与计算发展前沿, 2019,1(1):11-21.

[本文引用: 1]

[15]

张云泉, 袁良, 袁国兴, 李希代. 2019年中国高性能计算机发展现状分析与展望
[J]. 数据与计算发展前沿, 2020,2(1):18-26.

[本文引用: 1]

[16]

钱德沛. 构建支撑科技创新的新一代计算基础设施
[J]. 数据与计算发展前沿, 2020,2(1):1-17.

[本文引用: 1]