 ,1,2, 李俊
,1,2, 李俊 ,1,*
,1,*Computation Offloading Strategy for Multi-Base Station and Multi-User Equipment Mobile Edge Computing
Shi Yueru ,1,2, Li Jun
,1,2, Li Jun ,1,*
,1,*通讯作者: 李俊(E-mail:jlee@cstnet.cn)
收稿日期:2020-03-2网络出版日期:2020-06-20
| 基金资助: |
Received:2020-03-2Online:2020-06-20
作者简介 About authors

时月茹,中国科学院计算机网络信息中心,在读硕士研究生,主要研究方向为云计算、移动边缘计算。
本文贡献:理论分析,代码实现及测试,论文写作。
Shi Yueru is currently a master student at Computer Network Information Center of Chinese Academy of Sciences. Her main research interests are cloud computing and mobile edge computing.
In this paper, she undertakes the following tasks: theoretical analysis, code implementation, testing, and paper writing.
E-mail:

李俊,中国科学院计算机网络信息中心,研究员,博士生导师,中国科学院特聘研究员。主要研究方向为人工智能和大数据应用、互联网体系结构。
本文贡献:研究指导,论文结构组织。
Li Jun, specially appointed researcher of Chinese Academy of Sciences, is currently a research fellow and PhD supervisor at Computer Network Information Center of Chinese Academy of Sciences. His main research interests are artificial intelligence and big data technical applications and future Internet architecture.
In this paper, he undertakes the following tasks: research guidance, and paper structure organization.
E-mail:

摘要
【目的】计算卸载是移动边缘计算(MEC)的重要研究领域,弥补了设备在存储、计算等方面的不足,受到广泛关注。本文研究MEC密集网络的计算卸载策略。【方法】针对多基站多用户场景,提出了具备服务缓存和资源调度特征的卸载模型,采用动态规划和博弈论对缓存问题和通信计算资源的联合分配问题分别进行处理,实现用户之间相互满意的纳什均衡状态。【结果】通过仿真实验,证明了该策略的有效性,明显降低开销,提升系统性能,更好地满足用户需求。【结论】适用于移动边缘计算场景,为后续的计算卸载研究提供了理论和实践支持,下一步工作将引入激励机制对用户卸载行为的影响。
关键词:
Abstract
[Objective] Computation offloading is an important research area of Mobile Edge Computing (MEC). It makes up for the shortcomings of devices in storage and computation, thus receiving extensive attention. This paper studies the computation offloading strategy for MEC with dense network. [Methods] For the multi-base station and multi-user equipment scenario, we construct a computation offloading model with service caching and resource allocating features, and adopt dynamic programming and game theory to solve the caching problem and jointly allocate radio and computational resources. Finally, a Nash equilibrium state of mutual satisfaction achieves among users. [Results] Simulation experiments show that the proposed strategy is efficient to reduce overhead, improve system performance and can receive better satisfaction. [Conclusions] It is suitable for mobile edge computing scenario, and provides theoretical and practical supports for subsequent research on computation offloading. In the next step, we will consider the incentive mechanism to users’ behavior when discussing computation offloading.
Keywords:
PDF (14461KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
时月茹, 李俊. 多基站多用户场景的移动边缘计算卸载策略. 数据与计算发展前沿[J], 2020, 2(3): 126-136 doi:10.11871/jfdc.issn.2096-742X.2020.03.011
Shi Yueru, Li Jun.
引言
随着5G和物联网的蓬勃发展,智能终端设备不断涌现,网络边缘数据以爆炸式增长[1]。然而,其中大部分设备的计算和存储能力有限,在处理边缘数据时无法满足时延敏感、计算密集的需求,需要卸载(offload)到服务器平台上处理。以云计算模型为核心的集中式数据处理技术将这一卸载过程商业化,表现出明显的可扩放性和自治性[2]。通过按需付费,云计算用户可以使用虚拟资源池中的动态资源,将任务卸载到云平台上处理,再在设备端接收处理结果。这种软件即服务(software as a service)的新体验,免去了用户的硬件部署和资源操控环节[3],成为产业界和学术界的研究热点。但是,考虑到云计算的固有局限性,即任务经过漫长的传输距离到达云平台后才能被处理[4],云计算不再适用于时延要求极高且应用逐渐广泛的新兴场景,例如AR/VR、人脸识别、动态内容交付等。与此同时,万物互联[5]产生了海量的边缘数据,若全部通过云计算处理,将给骨干网带来巨大的带宽压力。涉及到个人隐私的数据如果被卸载到云平台,也会加大安全风险[6]。
为此,Satyanarayanan等人[7]在2009年提出Cloudlet的概念,通过将计算能力强的服务器部署在无线网络边缘,为附近的移动设备提供轻量级服务。Cloudlet被视作移动边缘计算的雏形[8]。2014年,欧洲电信标准化协会正式提出移动边缘计算的概念,并发布白皮书。相比于云计算,移动边缘计算具有明显优势[9]:1)时延低。MEC场景下,节点之间的距离更短,网络传输协议也更简单,减少了流量控制和路由转发操作,降低了各个节点的传输和通信时延;2)情景感知(context awareness)。MEC服务器能够利用短距离优势,收集丰富的实时数据,了解、掌握用户的行为习惯和生活喜好,根据不同的情景提供个性化服务;3)安全性高。云平台属于大型的公共数据中心,信息资源集中,且用户没有管理权限,很可能成为安全攻击的目标,移动边缘计算则规避了这些问题。
作为移动边缘计算的重要研究领域,计算卸载通过将任务卸载到服务器的方式,拓展了设备的计算和存储能力,帮助用户获得更加优质的服务体验[10]。在MEC系统中,为每位用户制定合适的卸载策略,是计算卸载的研究核心。2011年,Lagerspetz等人[11]进行了计算卸载的初步尝试,并归纳得到基本原则:数据量小、计算量大的任务在可用带宽充足的条件下,应当被卸载。但是这一结论仅考虑能耗对用户体验的影响,而在移动边缘计算中,时延也是非常重要的影响因素。Yang等人[12]从多用户角度,研究了时延和能耗的权衡优化问题,通过概率转移矩阵预测用户的请求分布,提出基于贪心的在线卸载策略。Sundar等人[13]将存在链式依赖关系的多个任务作为卸载对象,通过启发式算法优化二进制松弛解,有效地提高了收敛速度。但是上述文献没有考虑资源争夺产生的通信干扰问题。
无线通信资源的争夺是MEC网络的典型特征。如果多个设备同时选择将任务卸载到服务器,传输信道将被大量占用,引发严重的同频干扰,导致资源浪费。Wang等人[14]提出一种解决方案:首先比较任务的执行开销等决定是否卸载,再结合图着色算法分配物理资源块(physical resource block),接着最小化时延实现计算资源的优化分配。Liu等人[15]引入排队论,构建MEC系统多目标优化模型,通过设置权重转化为单目标问题,并借助标量化方案和内点法解决了这一问题。但是上述文献没有考虑MEC服务器处理不同类型的服务请求时,必须满足的先决条件。实际上,只有提前缓存了服务的源信息、相关数据库和程序包等,才能在对应类型的请求到达后做出处理[16]。另外,MEC服务器一般由具备计算和存储能力的小型基站担任[17],因此服务器的存储空间是有限的,同一时刻允许缓存的服务数据也是有限的,需要根据具体的MEC场景审慎选择,缓存最有利于用户的服务集合。
本文描述多个基站和多位用户的移动边缘计算卸载场景,根据任务请求的分布情况,解决基站的服务缓存问题和用户的个性化需求问题,实现各位用户的开销最小化。本文的主要贡献如下:
(1)介绍MEC计算卸载研究成果,对蜂窝同频小区拓扑形成的移动边缘计算卸载场景建模,提出多基站多用户的计算卸载问题,命名为COmP(Computation Offloading with multiple base stations and user equipment Problem),并给出解决方案;
(2)将服务缓存过程抽象为一维的0/1背包模型,通过动态规划建立递归关系,帮助基站挑选待缓存的服务,采用多人博弈联合优化通信和计算资源,经过有限次迭代后,用户做出相互满意的开销最小化决策,系统达到纳什均衡状态。
1 MEC系统模型
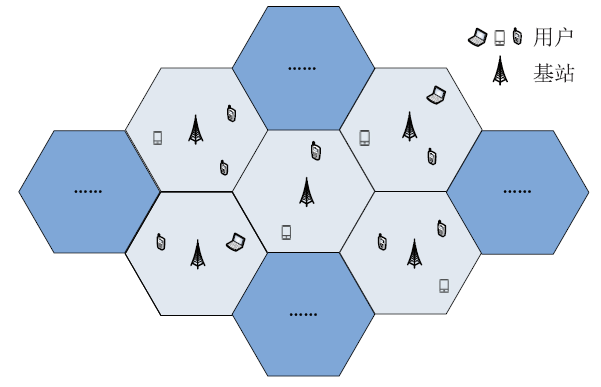
移动边缘计算卸载场景如图1所示。本场景共包括B个蜂窝同频小区,每个小区内有一个基站和数位用户,分别介绍如下:图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1移动边缘计算卸载场景
Fig.1Scenario of computation offloading of MEC
(1)基站。每个基站的信号覆盖范围与所在小区的划分范围一致,不存在重叠现象。作为MEC服务器,基站具备较强的计算和存储能力,可以为小区内的用户提供服务,满足多种类型的用户需求,但必须提前缓存对应类型的服务数据;
(2)用户。一位用户就是一个用户设备(user equipment)。相比于基站,设备的计算和存储能力较弱,在处理任务请求时,需要考虑是否将任务卸载到基站。每个设备允许请求多个排队等待的任务,但要求它们相互独立,没有先后依赖关系。
为了方便讨论,本文引入准静态概念[18]。每个准静态阶段一般持续几百毫秒,处在该阶段时,每位用户的位置固定,并且请求一项任务。只有过渡到下一个准静态阶段,才会更新用户的位置坐标和任务请求,基站也会更新缓存的服务集合。选取任一准静态阶段作为研究对象,构建计算卸载模型,将建模过程涉及的常量参数汇总如表1所示。
Table 1
表1
表1移动边缘计算常量参数表
Table 1
| 参数 | 含义 |
|---|---|
| $\mathcal{N}=\{1,2,3,\dots,N\}$ | 设备集合 |
| $\mathcal{B}=\{1,2,3,\dots,B\}$ | 基站集合 |
| $\mathcal{M}=\{1,2,3,\dots,M\}$ | 服务类型集合 |
| $\mathcal{K}=\{1,2,3,\dots,K\}$ | 无线传输子信道集合 |
| $\mathcal{O}_{b}$ | 基站$b$信号覆盖范围内的设备集合 |
| $\mathcal{D}_{n}$ | 设备$n$可选择的卸载基站集合 |
| $\phi_{b,m},\varphi_{b,m}$ | 基站$b$与服务类型$m$的匹配度修正因子 |
| $T_{n}$ | 设备$n$请求执行的任务 |
| $\xi_{n},\zeta_{n}$ | 设备$n$的个性化需求因子 |
| $is_{n,m}$ | 任务$T_{n}$是否属于服务类型$m$ |
| $d_{n}$ | 任务$T_{n}$的数据输入量 |
| $\Phi_{n}$ | 执行$T_{n}$所需的CPU时钟周期 |
| $k_{n}^{loc}$ | 设备$n$每个时钟周期的能量消耗 |
| $f_{n}^{loc}$ | 设备$n$的CPU时钟频率 |
| $k_{b}^{off}$ | 基站$b$每个时钟周期的能量消耗 |
| $f_{b}^{off}$ | 基站$b$的CPU时钟频率 |
| $B_{b}$ | 基站$b$允许缓存服务的最大空间 |
| $M_{m}$ | 缓存服务类型$m$所需的基站空间 |
| $W_{0}$ | 单个子信道的带宽 |
| $P_{0}$ | 背景白噪声功率 |
| $p_{n}^{k}$ | 设备$n$在子信道$k$上的数据发送功率 |
| $g_{n}^{b}$ | 设备$n$与基站$b$的信道增益 |
新窗口打开|下载CSV
1.1 服务缓存
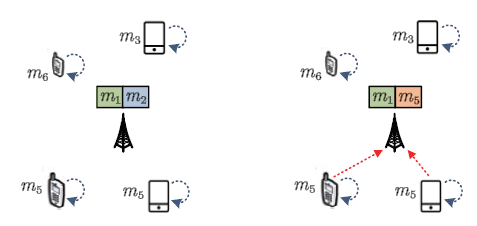
服务缓存是实现移动边缘计算卸载的重要环节。对于MEC系统来说,基站缓存的服务集合的好坏,直接影响最终的卸载决策。如图2所示,4位用户请求的任务分别属于类型$m_{3}$、$m_{5}$、$m_{5}$和$m_{6}$。左图假设基站缓存了$m_{1}$和$m_{2}$的服务数据,以此为条件,4位用户均无法获得来自基站的帮助,即使设备处在低电量的极端状态,用户也只能做出本地执行的卸载决策。右图则假设基站缓存的服务类型为$m_{1}$和$m_{5}$,那么至少有2位用户获得了将任务卸载到基站的机会,可以在自身能力不足的情况下选择基站执行任务。图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2服务缓存效果比较
Fig.2Comparison of service caching
因此,基站应当在服务缓存环节审慎选择。为保证服务质量,需要衡量每个基站与每种服务类型的匹配度。本文定义$\Gamma_{b,m}$为衡量参数,则
其中,$\sum\limits_{n\in \mathcal{O}_{b}}is_{n,m}\Phi_{n}$、$\sum\limits_{n\in \mathcal{O}_{b}}is_{n,m}d_{n}$分别表示基站$b$的信号覆盖范围内,所有属于服务类型$m$的任务请求的CPU计算总周期和数据输入总量。$\phi_{b,m}$、$\varphi_{b,m}$均为匹配度的修正因子,描述了基站与服务之间可能存在的特殊关系,一般取$\phi_{b,m}=\varphi_{b,m}=1$。在其他条件一定时,基站$b$与服务类型$m$的匹配参数$\Gamma_{b,m}$值越大,该服务越倾向于被基站缓存。
将$B$个基站的服务缓存结果记作$\Theta$,则
其中,$\Theta_{b}$表示基站$b$的服务缓存结果,由匹配度$\Gamma_{b,m}$、基站容量$b_{b}$和服务体积$M_{m}$共同决定。
1.2 资源调度
服务缓存结束后,MEC系统进入资源调度环节。给定$N$位用户的决策集合$\Lambda$,则对于用户$n$来说,向量$\Lambda_{n}$代表着最终的卸载决策。特别地,$\Lambda_{n}=(0,0)$表示用户选择在本地执行任务,拒绝将任务卸载到基站。
1.2.1 通信模型
用户在本地执行任务时,无需考虑通信过程,但当用户做出卸载任务到基站的决策时,考虑到任务的上传和下载问题,需要构建通信模型。由于大部分的任务请求,例如语音识别、认知辅助等,输出结果都远小于输入的数据规模,因此,类似于文献[19]和[20],本文只研究数据上传过程中的通信开销而忽略下载过程。
用户通过无线信道,将执行任务所需的数据上传到基站。小区内的无线信道采用同频方式部署,频带被等分为$K$个相互正交的子信道,准静态条件又要求每位用户仅能选择单个子信道与单个基站建立连接关系,相应地,用户$n$请求的任务沿着子信道$k$卸载到基站$b$的信号与干扰加噪声比为
式(12)考虑了MEC用户复用相同的子信道,可能产生的信号干扰,再引入香农频谱公式[21],得到数据的传输速率为
式(14)说明卸载的用户数目与传输速率成负相关关系。如果已经有较多的用户选择卸载,那么不建议卸载用户的继续加入,甚至需要将部分“基站执行”的用户决策调整为“本地执行”,以降低无线信道的干扰影响。另外,通信过程是一个消耗时间和能量的过程,时延和能耗分别为
根据式(16)和式(17)可知,用户$n$将任务卸载到基站的通信总开销为
其中,$\xi_{n}$、$\zeta_{n}$表示用户$n$请求任务的个性化需求因子。$\xi_{n}$、$\zeta_{n}$值的不同,对应于不同的任务执行标准。若$\xi_{n}$趋近于1且$\zeta_{n}$趋近于0,那么该任务属于时延敏感型,用户对时延要求更高,希望尽快得到输出结果。反之,该任务属于能耗敏感型,用户对能耗要求更高,希望保留更多的设备电量。当然,如果用户没有特殊要求,可以设置$\xi_{n}=\zeta_{n}=0.5$。
1.2.2 计算模型
将用户$n$请求的任务记作$T_{n}\triangleq (d_{n},\Phi_{n})$,并调用图分析技术确定$d_{n}$、$\Phi_{n}$的值[22]。任务$T_{n}$可以选择在本地执行,也可以卸载到基站执行,对应的计算模型分别为:
(1)本地计算模型。设备拥有一定的计算和存储能力,可以执行自身请求的任务,时延为
任务执行过程中消耗的能量降低了设备的工作时长,进而被用户感知,则
其中,$\kappa_{n}^{loc}$与设备$n$的硬件构成有关,可通过文献[23]提供的方法获得。
(2)基站计算模型。基站的计算和存储资源更为丰富,只要提前缓存了对应类型的服务数据,就可以在任务卸载到基站后做出处理。与本地执行类似,基站处理任务的时延和能耗分别为
需要说明的是,本文从用户角度构建了计算卸载模型,而$ e_{n}^{off}$代表基站的能量开销,不会被用户感知,因此不纳入考虑范围,则
根据式(27)和式(28)可知,执行任务$T_{n}$所需的计算总开销为
s.t. 式(19)~式(21)
1.3 COmP优化目标
在计算卸载过程中,每个基站根据信号覆盖范围内的用户请求,缓存合适的服务集合,每位用户则根据基站缓存的服务情况,比较本地执行和卸载到基站执行的开销,并以较低的开销方式完成任务。针对蜂窝同频小区拓扑形成的移动边缘计算卸载场景,COmP将$B$个基站和$N$位用户作为研究对象,目标是最小化各位用户的可感知开销,其数学形式为s.t. 式(1)~式(30)
ComP问题的研究面向整个MEC系统,因此,实现用户开销最小化的系统最优解为
2 问题解决
本文将COmP分解为服务缓存和资源调度两个子问题,根据不同的问题特征设计解决方案,确定基站缓存的服务集合$\Theta^{*}$和用户的卸载决策$\Lambda^{*}$。2.1 动态规划
为了帮助基站高效地缓存服务数据,引入移动边缘计算场景下的0/1背包问题。将基站$b$视作一个等待物品装入的背包,背包的最大存储空间为$B_{b}$,$M$种不同类型的服务是$M$件等待装入的物品,第$m$件物品的体积为$M_{m}$,价值为$Gamma_{b,m}$。现要求挑选数件物品放入背包,使得背包的总价值最大。该问题可表示为其中,$ x_{i}$的取值范围保证了每一种类型的服务数据都不会被重复缓存或部分缓存。
0/1背包问题具有最优子结构,可以通过动态规划建立递归关系,自底向上地构造出最优解。具体来说,动态规划将原问题转化为多个结构相似的子问题,不断使用新的子问题的解替换现有结果,逐步接近乃至确定最优解。本文定义变量$f_{C_{b},I}$,表示仅能挑选第1件到第$I$件的物品($1<I\le M$)放入背包且总体积不超出$C_{b}$时,背包的最大价值量,则
式(36)即为原问题和子问题最优解之间的递归关系。根据子问题的物品挑选情况,可以递归得到$I=M$的解,进而确定基站$b$的服务缓存集合\Theta_{b}^{*}。给出动态规划方案如算法1所示。
算法1
算法1确定基站的服务缓存集合$\Theta^{*}$
 |
新窗口打开|下载CSV
2.2 多人博弈
移动边缘计算场景下的每一位用户都是理性个体,只关心自己的利益,将执行自己的任务需要付出的开销作为是否卸载的衡量标准,而不关心其他用户的开销情况。但数据在上传的过程中存在信号干扰,这意味着各个任务的执行开销相互影响,用户需要先计算出其他$N-1$位用户的卸载决策产生的干扰强弱,再由此做出自己的个性化决策。考虑到不同用户对于服务的偏好有所不同,MEC系统中不会自发形成用户间的合作关系,甚至可能出现较大范围的资源争夺现象。博弈论能够帮助理性的参与者根据已知信息和偏好关系确定下一步的行动计划,不断迭代直至系统达到稳定状态。相应地,博弈论适用于解决上述的用户决策问题。令
表示用户集合$\mathcal{N}=\{1,2,3,\dots,N\}$中除了用户$n$之外,其他用户的卸载决策,那么用户$n$做出个人决策$\Lambda_{n}$的偏好依据可以表示为
引入博弈论工具,可得$N$位用户非合作型博弈的元组形式为
其中,$ \Delta_{n}$表示用户$n$可选择的卸载策略集合,$U_{n}$表示用户$n$的可感知开销函数。
纳什均衡在博弈论研究中占有重要地位。处在纳什均衡状态时,对于任意用户$ n\in \mathcal{N}$,如果只改变$\Lambda_{n}$而保持$\Lambda_{-n}$不改变,需要付出的开销值不会更小。因此,如果其他用户的卸载决策保持不变,足够理性的用户没有理由打破这种均衡局面。接下来,对移动边缘计算场景下多人博弈的纳什均衡做出定义。
定义1 $N$位用户的决策集合$\Lambda^{*}$是博弈过程$\Psi$的一个纳什均衡,若满足
根据这一概念定义可知,如果MEC系统处于纳什均衡状态,那么用户无法通过改变卸载决策继续降低开销值,即实现了COmP问题的优化目标。
$\Psi$博弈一定存在纳什均衡点。这是因为MEC系统中的多人博弈属于势博弈,每位用户的开销改变都会映射到一个全局的单调势函数上[24],而势博弈的特征之一就是经过有限次数的迭代后必定达到纳什均衡状态。给出多人博弈方案如算法2所示,为了简化博弈过程,本文设置了博弈参与条件,且要求每轮迭代只有一位用户修改自己的卸载决策。
算法2
算法2确定用户的卸载决策集合$\Lambda^{*}$
 |
新窗口打开|下载CSV
3 实验结果与分析
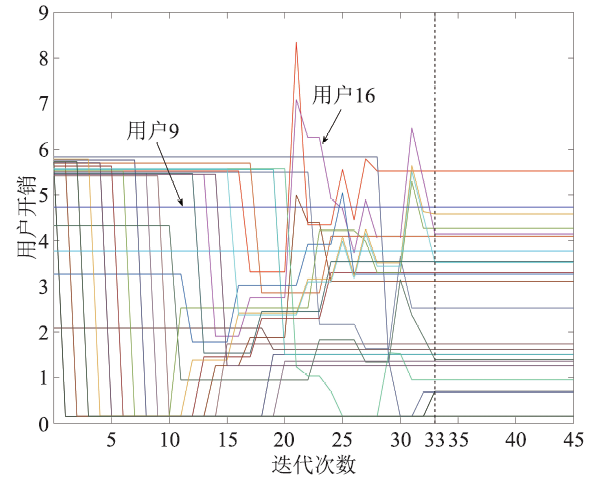
通过Matlab R2015b平台验证算法的有效性。在MEC仿真系统中,每个蜂窝小区的单边长度为30m,基站位于小区的中心,信号覆盖范围与小区范围一致。基站与用户之间的距离dis取[$10\sqrt{3},30$]m中的随机值,信道增益$g_{n}^{b}=dis^{-\rho}$,$\rho=4$为路径损耗指数。设备的发送功率为3W,背景噪声为-100dBm,传输子信道带宽为2MHz。另外,除非文中给出特殊说明,否则取$\xi_{n}=\zeta_{n}=0.5$。图3展示了N=25时,各位用户的任务执行开销随迭代次数变化的趋势。其中,共有2位用户不参与迭代,以用户9为例,他的开销始终是定值,这是因为基站没有提前缓存该用户请求的服务,用户未能获得博弈的机会。其余的23位用户则参与了迭代,以用户16为例,他的开销变化并不是单调的,这是因为每轮迭代只允许一位用户修改自己的卸载决策,但所有的博弈用户都会受到该用户决策改变的影响,这一影响可能带来开销值的降低、增长或者不变。根据图3可知,经过33轮迭代后,MEC系统达到纳什均衡状态。
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3用户开销变化
Fig.3Change of users’ overhead
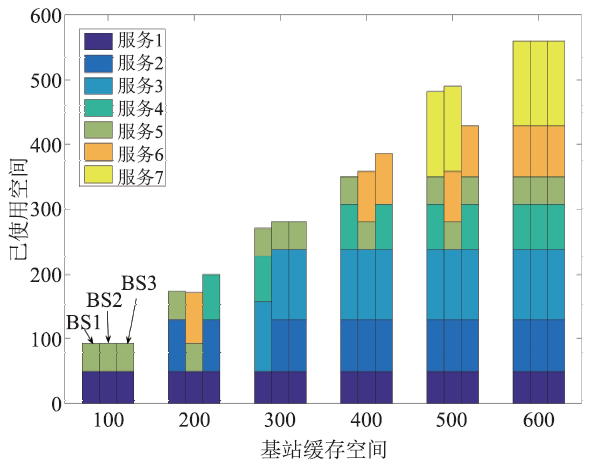
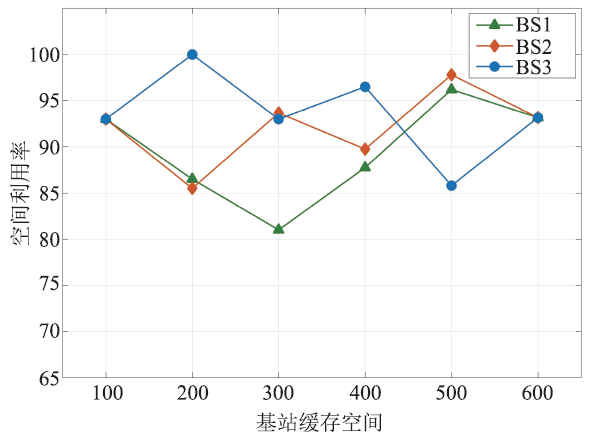
在三个小区内分别部署基站BS1、BS2和BS3,不同基站根据信号覆盖范围内的用户请求缓存服务的情况如图4和图5所示。实验结果表明,面对用户的个性化请求,基站的最低空间利用率为81%,平均空间利用率为92%,缓存空间得到了灵活且高效地利用。需要注意的是,缓存空间取值为600时,BS1、BS2和BS3已经缓存了全部类型的服务,即使继续扩大缓存空间,各基站缓存的服务集合依然保持不变。
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4基站服务缓存结果
Fig.4Cached service of BSs
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5基站空间利用率
Fig.5Space utilization of BSs
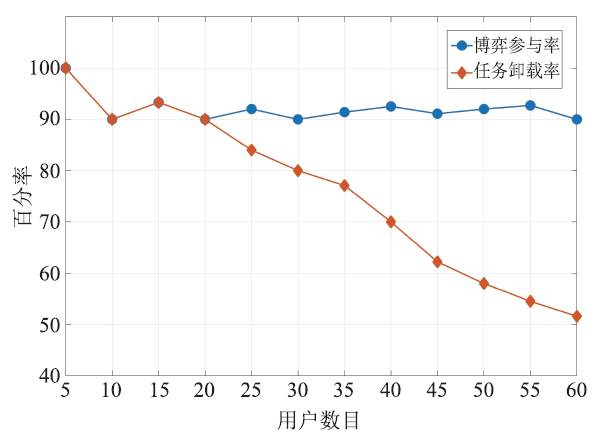
图6展示了不同的用户数目对于博弈参与率和任务卸载率的影响。根据图6可知,小区用户从5位增加至60位,但参与率一直保持在90%以上,证明了算法的有效性。另一方面,在用户数目较少的情况下,MEC系统允许所有参与博弈的用户将任务卸载到基站,此时参与率与卸载率相等,而随着用户的不断加入,无线信号干扰严重,因此从25位用户开始,卸载率与参与率不再相等,越来越多的用户选择本地执行任务。若要缓解这一问题,可以考虑部署更多的子信道。
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6博弈效果比较
Fig.6Comparison of games
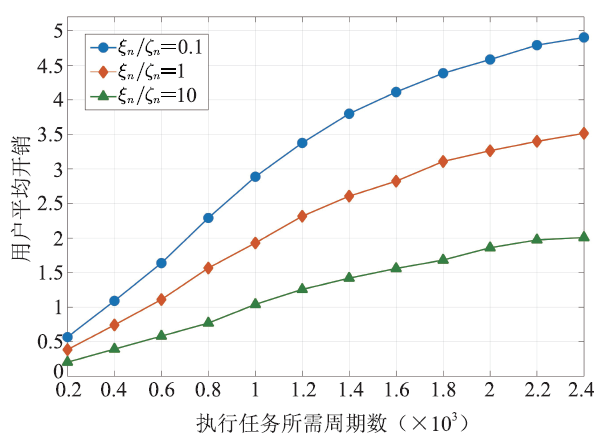
图7展示了个性化需求因子与用户平均开销的关系。这里,$\xi_{n}$、$\zeta_{n}$的取值对于任意$n \in \mathcal{N}$都成立,且$\xi_{n}$、$\zeta_{n}$总和恒为1,因此$\xi_{n}/\zeta_{n}=0.1$表示能耗敏感型而$\xi_{n}/\zeta_{n}=10$表示时延敏感型任务。图7显示,随着周期数的增加,执行任务花费的开销越来越大,但$\xi_{n}/\zeta_{n}=10$时的开销值始终低于$\xi_{n}/\zeta_{n}=0.1$和$\xi_{n}/\zeta_{n}=1$,说明在给定的参数条件下,能耗对于用户可感知开销的影响远超出时延影响,这也是必须引入个性化需求因子的重要原因。
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7个性化需求因子对用户平均开销的影响
Fig.7Impact of weighting parameters on overhead
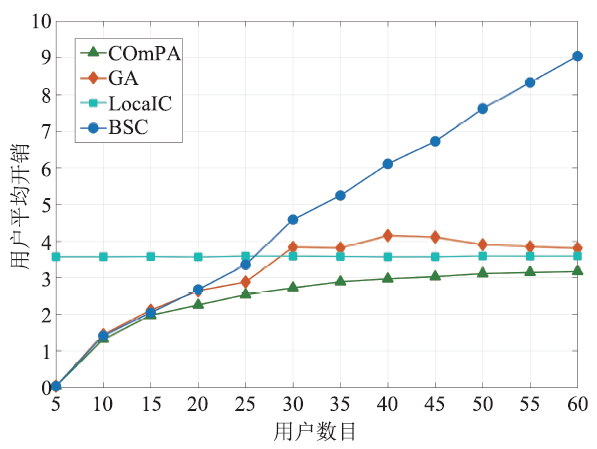
将本文的卸载策略COmPA(COmP Algorithm)与另外三种算法作对比,结果如图8所示。其中,GA(Greedy Algorithm)表示贪心算法,用户总是选择当前看来开销最小的决策,并认为是最优决策;LocalC(Local Computing)表示本地执行算法,用户请求的任务在自己的设备上执行,不考虑卸载的可能性;BSC(Base Station Computing)表示基站执行算法,用户选择一条子信道,将请求的任务卸载到基站后执行。从图8可以看出,在用户数目相同的条件下,COmPA性能明显优于其他算法,用户平均开销相比GA、LocalC和BSC,最高分别节省28%、98%和64%。但随着小区内用户的增加,大部分用户不再选择将任务卸载到基站,而是直接本地执行,因此COmPA的开销值逐渐接近LocalC。
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8算法性能比较
Fig.8Comparison of algorithms for MEC
以上仿真实验说明了COmPA适用于移动边缘计算的计算卸载问题,能够提升基站的缓存空间利用率,增加博弈的参与人数,优化用户的卸载决策,同时具有较高的鲁棒性,可以满足不同用户的个性化需求。相比于GA、LocalC和BSC等典型算法,COmPA也能显著降低用户的卸载开销。
4 结束语
本文针对多个基站和多位用户的密集网络场景,研究移动边缘计算卸载策略。根据用户的请求分布,按照任务执行过程构建计算卸载模型,采用动态规划缓存服务数据,并采用多人博弈实现通信和计算资源的优化分配,从而降低用户的卸载开销,提升MEC系统性能。仿真结果表明,经过有限次数的迭代后系统实现纳什均衡,计算卸载问题得到有效解决。在下一步的工作中,将引入激励机制,讨论部分用户受到激励而联合行动的卸载现象。利益冲突声明
所有作者声明不存在利益冲突关系。参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[EB/OL].[
URL [本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[C]//
[本文引用: 1]
[J].
[本文引用: 1]
[J].
DOI:10.1109/COMST.2017.2682318URL [本文引用: 1]
[J].
DOI:10.1109/COMST.2017.2745201URL [本文引用: 1]
[J].
[本文引用: 1]
[C]//
[本文引用: 1]
[J].
[本文引用: 1]
[C]//
[本文引用: 1]
[J].
DOI:10.1109/TVT.2017.2672701URL [本文引用: 1]
[C]//
[本文引用: 1]
[C]//
[本文引用: 1]
[C]//
[本文引用: 1]
[C]//
[本文引用: 1]
[C]//
[本文引用: 1]
[J].
DOI:10.1109/ACCESS.2017.2710056URL [本文引用: 1]
[M].
[本文引用: 1]
[J].
DOI:10.1109/TNET.2015.2487344URL [本文引用: 1]
[C]//
[本文引用: 1]
[J].
DOI:10.1006/game.1996.0044URL [本文引用: 1]
