适合一类复杂异构超算系统的HPL并行计算模型研究

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-02

赵海涛, 孙家昶, 黎雷生, 杨文浩, 赵慧, 李会元^,^*中国科学院软件研究所,并行软件与计算科学实验室,北京 100190

Research on HPL Parallel Computing Model for a Class of Complex Heterogeneous Supercomputer System

Zhao Haitao, Sun Jiachang, Li Leisheng, Yang Wenhao, Zhao Hui, Li Huiyuan^,^*Laboratory of Parallel Software and Computational Science, Institute of Software, Chinese Academy of Sciences,Beijing 100190, China

通讯作者: * 李会元（E-mail:huiyuan@iscas.ac.cn）

收稿日期:2019-12-18网络出版日期:2020-02-20

基金资助:

国家重点研发计划高性能计算重点专项“适应于E级计算的可计算物理建模与新型计算方法”.2016YFB02006010
国家重点研发计划高性能计算专项.2018YFB0204404
中国科学院战略性先导科技专项.XDC01030200

Received:2019-12-18Online:2020-02-20
作者简介 About authors

赵海涛,中国科学院软件研究所,博士,副研究员,主要研究方向为高性能工程与科学计算。
本文承担工作为：并行计算模型建立与分析。
Zhao Haitao, Ph.D., is an associate researcher at Institute of Software, Chinese Academy of Sciences. His main research direction is high performance engineering and scientific computing.
In this paper he undertakes the following tasks: establishment and analysis of parallel computing model.
E-mail: haitao@iscas.ac.cn

孙家昶,中国科学院软件研究所,博士,首席研究员,主要研究方向为高性能计算。
本文承担工作为：并行计算模型研究。
Sun Jiachang, Ph.D., is a chair professor at Institute of Software, Chinese Academy of Sciences. His main research direction is high performance computing.
In this paper he undertakes the following tasks: research on parallel computing model.
E-mail: jiachang@iscas.ac.cn

黎雷生,中国科学院软件研究所,博士,副研究员,主要研究方向为大规模并行科学与工程计算和异构加速计算。
本文承担工作为：HPL性能优化。
Li Leisheng, Ph.D., is an associate researcher at Institute of Software, Chinese Academy of Sciences. His main research direction is large-scale parallel scientific and engineering computing and heterogeneous accelerated computing.
In this paper he undertakes the following tasks: HPL performance optimization.
E-mail: leisheng@iscas.ac.cn

杨文浩,中国科学院软件研究所,硕士,实习研究员,主要研究方向为高性能计算。
本文承担工作为：HPL性能优化。
Yang Wenhao, Master, is an intern researcher at Institute of Software, Chinese Academy of Sciences. His main research direction is high performance computing.
In this paper he undertakes the following tasks: HPL performance optimization.
E-mail: wenhao@iscas.ac.cn

赵慧,中国科学院软件研究所,博士,助理研究员,主要研究方向为高性能工程与科学计算。
本文承担工作为：HPL性能测试。
Zhao Hui, Ph.D., is an assistant researcher at Institute of Software, Chinese Academy of Sciences. Her main research direction is high performance engineering and scientific computing.
In this paper he undertakes the following tasks: HPL performance test.
E-mail: zhaohui2016@iscas.ac.cn

李会元,中国科学院软件研究所,博士,研究员,主要研究方向为工程与科学计算。
本文承担工作为：并行计算模型研究。
Li Huiyuan, Ph.D., is a researcher at Institute of Software, Chinese Academy of Sciences. His main research direction is engineering and scientific computing.
In this paper he undertakes the following tasks: research on parallel computing model.E-mail：huiyuan@iscas.ac.cn

摘要
【目的】为快速分析超算系统性能,加速HPL基准测试优化,本文分析了HPL主要影响因素,建立了相关并行计算模型。【方法】基于曙光先进计算系统HPL基准测试程序并行优化,采用理论分析与实验验证相结合的方法,分别对HPL效率上限、快速预测、不同参数影响等问题进行分析,建立了相应的并行计算模型。【结果】与曙光先进计算系统测试结果进行对比,预测结果与实测结果吻合较好,表明了计算性能与任务的均衡度、矩阵操作占HPL计算比率、矩阵操作效率、矩阵操作库函数利用率以及网络传输等能够较大程度反映超算系统HPL的计算效率,加速卡的矩阵操作效率与HPL的效率成正比关系。【局限】目前并行计算模型考虑因素还不全面,大规模计算系统稳定性带来的性能影响还需要进一步研究。【结论】基于不同预测需求的并行计算模型,对HPL基准测试性能预测、并行优化具有重要的指导意义。
关键词： HPL;并行计算模型;异构系统;计算效率;预测

Abstract
[Objective] In order to quickly analyze the performance of the supercomputing system and accelerate the optimization of HPL benchmark tests, this paper analyzes the main influencing factors of HPL and establishes a related parallel computing model. [Methods] Based on the parallel optimization test results of the Sugon advanced computing system HPL benchmark, the method of combining theoretical analysis and experimental verification is used to analyze the HPL efficiency upper limit, fast prediction, and influence of different parameters, on which the corresponding parallel calculations model is established. [Results] Compared with the test results of the Sugon advanced computing system, the prediction results are in good agreement with the actual measurement results, indicating the balance between factors such as computing performance and tasks, the ratio of matrix operations to HPL calculation, the efficiency of matrix operations, the utilization of matrix operation library functions, network transmission and so on can largely reflect the calculation efficiency of the HPL of the supercomputing system. Besides, the matrix operation efficiency of the acceleration card is directly proportional to the efficiency of the HPL. [Limitations] At present, the design of parallel computing models are not comprehensively considered, and how the stability requirements of a large-scale computing system affects its performance needs further studies. [Conclusions] Parallel computing models based on different forecasting requirements have important guiding significance for HPL benchmark performance prediction and parallel optimization.
Keywords：HPL;parallel computing models;heterogeneous system;computing efficiency;prediction

PDF (6478KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
赵海涛, 孙家昶, 黎雷生, 杨文浩, 赵慧, 李会元. 适合一类复杂异构超算系统的HPL并行计算模型研究. 数据与计算发展前沿[J], 2020, 2(1): 85-92 doi:10.11871/jfdc.issn.2096-742X.2020.01.007
Zhao Haitao. Research on HPL Parallel Computing Model for a Class of Complex Heterogeneous Supercomputer System. Frontiers of Data and Computing[J], 2020, 2(1): 85-92 doi:10.11871/jfdc.issn.2096-742X.2020.01.007

引言

High-Performance Linpack Benchmark（HPL）结合了LAPACK和ScalLAPACK的技术,是国际上最流行的用于评测高性能计算机浮点运算性能的Benchmark,对大型并行计算系统的稳定性测试也有很重要的参考价值。它由美国田纳西大学计算机系教授Dongarra提出^[3],全球超级计算机TOP500^[1]和我国高性能计算机TOP100^[2]均按照HPL实测的持续性能进行排名。国内外****在超算系统的研制以及HPL性能优化中,都对HPL的并行计算模型开展了相关研究。如2003年罗水华等人对HPL的影响因素进行了分析^[4];2006年张文力等人基于计算系统设计需求对内存、带宽、延迟等对HPL的影响进行了研究^[5];2011年王锋等人在GPU加速卡的TianHe-1上开展了HPL的并行优化研究^[6,7];2012年王申等人基于神威蓝光和神威4000A超算系统分析了HPL各部分计算效率以及传输效率等影响因素,对HPL的性能和效率进行了预测^[8];2013年Alberto Cabrera等人通过HPL计算模型入手分析了计算与能耗的相关关系^[9];2018年贾迅等人针对异构系统HPL性能和高效异构架构设计需求,开展了高性能计算系统HPL效率受限因素分析工作^[10];甘新标等人针对HPL性能优化开展了国产加速器在超算系统上的协同设计相关研究^[11,12]。

随着并行计算系统越来越庞大,节点异构程度越来越高,网络拓扑关系越来越复杂,异构计算已被业界广泛应用^[13],传统的并行计算模型难以满足当前性能预测与大型并行计算系统的研制。如何确定当前CPU与加速卡之间计算性能差异大、内存大小不一致以及节点内CPU核间、加速卡间和节点间传输性能差异大等特性的强异构超算系统的并行计算模型,指导并实现HPL测试结果,结合曙光先进计算系统HPL研制任务,2018年我们提出了“起点高、中途稳、冲刺陡”的优化策略。本文基于中国科学院软件研究所在曙光先进计算系统上HPL优化结果,针对HPL效率影响较大的相关因素,建立能够快速反映超算系统HPL并行效率的并行计算模型。

1 High Performance Linpack异构系统并行计算模型

HPL采用高斯消元法求解线性代数方程组,整体浮点运算次数为LU分解的浮点运算次数2/3×N³-1/2×N²,回代解方程的浮点运算次数2×N²。HPL的计算时间主要包括PANEL分解、行交换、解下三角方程组（DTRSM）、矩阵乘（DGEMM）、广播开销未被隐藏的部分和回代;在大规模并行系统中,由于分解和回代部分的时间占总时间的比例非常小,其它三部分一般认为是影响计算效率的主要因素。

对单一计算系统的计算模型已经有了大量的研究成果,并且能够很好的分析和预估其计算效率。例如：单一由CPU构成的计算系统,假定N表示求解线性代数方程组的规模,NB为分块大小,P、Q分别为进程的行列数,α为网络延时,β为网络带宽, R_peak为计算系统理论峰值,w为计算系统执行矩阵乘的效率,γ₃为矩阵乘在HPL中所占的比率^[9]。

HPL总时间=计算时间+数据传输时间+网络延迟,即

（1）

T_{HPL} = \frac{2 N^{3}}{3 PQ R_{peak} w γ_{3}} + \frac{N^{2} (3 P + Q)}{2 PQβ} + α \frac{N ((NB + 1) \log (P) + P)}{NB}

随着超级计算机的发展,由于散热和功耗的限制,当前主流的超算系统已经由单一的CPU结构,转变为CPU与加速卡的混合结构,在计算部件、内存、基础软件、基础数学库效率等方面都有明显的差异,因而传统的并行计算模型已经难以反映这些异构系统的并行计算效率。我们基于当前超算系统强异构特点,进行系统分析,建立能够较好地反映超算系统的并行计算效率的并行计算模型,预测超算系统的计算效率上限,为HPL性能优化与预测提供一定的参考。

1.1 HPL计算效率上限分析

HPL作为超算系统标准测试程序,很大程度上反映了超算系统的实际计算能力;基于强异构系统CPU与加速卡之间的计算能力相差几十倍甚至近百倍的特点,HPL的并行程序优化在程序结构、线程设置、流水线控制等方面也需要采用更加精细的技术优化手段。对HPL效率的上限进行分析预测,就需要分析整个HPL求解过程中的各部分计算效率和时间,当前HPL计算的主要计算量就是矩阵乘法DGEMM的计算量,尤其在强异构超算系统上,尽量将HPL大块矩阵乘法的计算量放在加速卡上完成,已经成为HPL效率优化的主要手段,因此,HPL效率的上限与加速卡DGEMM的效率密不可分。在HPL计算过程中,随着矩阵规模的不断减小,DGEMM的计算效率也在不断变化,DGEMM所用时间与PANEL分解和数据传输的时间之间也在相应的变化。因此,HPL计算效率上限与计算阶段密切相关,可表述为一个分段函数形式：

（2）

\begin{matrix} η_{T \max} \geq η_{\max} \\ = \{\begin{matrix} η_{DGEMM} 0 \leq t \leq t^{*} \\ \begin{matrix} (1 - α_{t}^{k} - α_{t}^{n}) η_{DGEMM} \\ + α_{t}^{k} η_{PANEL} + α_{t}^{n} η_{NET} \end{matrix} t^{*} \leq t \leq t_{c} \end{matrix} \end{matrix}

其中,

η_{T \max}

为HPL理论最大效率,

η_{\max}

为HPL实测最大效率,

η_{GEMM}

为加速卡DGEMM的峰值效率,

η_{PANEL}

为PANEL分解的计算效率,

α_{t}^{k}

为在当前时间段PANEL效率的影响率,

η_{NET}

为网络传输性能,

α_{t}^{n}

为在当前时间段网络传输性能的影响率,

t_{c}

为计算总时长。

从中可以看出,在HPL测试过程中,在

t^{*}

时刻前,矩阵乘计算量大,其他计算和网络数据传输都可以被加速卡矩阵乘的计算时间所掩盖,因此,HPL的效率上限是加速卡DGEMM的效率;当在

t^{*}

后,随着加速卡上矩阵乘的计算量逐渐减小,其计算时间难以掩盖其他计算量和数据的传输时间,则HPL的效率上限就会受到PANEL分解的求解效率和网络传输性能的影响。

1.2 HPL效率快速分析方法

影响HPL的效率的因素较多,尤其在复杂的强异构超算系统上,如何快速预测HPL效率,判断超算系统的计算能力,一直是超算系统效率预测、系统应用和软件优化的研究热点。通过系统研究当前主流CPU和加速卡结构的超算系统,分析影响HPL效率的各影响因素,采用超算系统HPL效率

η

影响较大的五个因素来表达超算系统HPL效率,具体如下：

（3）

{η = {η_{s} η_{MM} η_{DGEMM} η}_{Lin} η}_{NET}

其中,η_s为超算系统计算能力与计算任务的均衡度;η_MM为矩阵操作占整体HPL计算的比率;η_DGEMM为矩阵操作库函数的效率;η_Lin为矩阵操作库函数的利用率;η_NET网络传输对HPL数据传输性能影响效率,根据不同的通信算法η_NET的值也有不同。

1.3 HPL计算量和通信量对计算时间的影响分析

理想状态下,如果能够持续为计算单元提供计算量,超算系统的计算效率就会被完美发挥,但是由于问题求解方法的特性,难免需要进行数据传输,计算量是难以时时都大于通信量的。通过对强异构超算系统计算能力和通信能力进行分析,也可以建立超算系统的并行计算模型效率,预估其计算效率：

（4）

\begin{matrix} η = \frac{T_{WN}}{T} = \frac{W_{N} / f_{c}}{W_{N} / f_{c} + ({α_{0} T}_{0} + α_{1} \frac{c_{2} N^{2} + c_{1} N}{W_{B}})} \\ = \frac{1}{1 + \frac{({α_{0} T}_{0} + α_{1} \frac{c_{2} N^{2} + c_{1} N}{W_{B}}) f_{c}}{W_{N}}} \end{matrix}

其中,T为HPL的计算时间;

T_{WN}

为HPL的理论计算时间,

T_{WN} = \frac{W_{N}}{f_{c}}

;

W_{N}

为计算量,

W_{N} = \frac{2}{3} N^{3} + \frac{3}{2} N^{2}

;

c_{2} N^{2} + c_{1} N

为通信量;

T_{0}

为网络延迟;

W_{B}

为数据传输的带宽;

f_{c}

为机器理论峰值;

α_{0}

为不能被掩盖的数据传输次数;

α_{1}

为不能被掩盖的数据传输量占总数据传输量的比率;

c_{2}

为矩阵数据传输量占矩阵整体的比例;

c_{1}

为向量数据传输量占向量整体的比例。

2 模型验证

超算软硬件系统建成后,HPL的性能和效率在一定程度上能够反映该系统整体特性。通过HPL的测试的计算效率,往往可以找出该超算系统在应用上的瓶颈,如何获得超算系统HPL的上限显得尤为重要。

2.1 预测与实测效率上限对比

在预测超算系统计算效率上限时,认为PANEL分解与网络传输影响最小,则主要影响因素就变为加速卡上DGEMM效率随不同矩阵规模的变化。我们简单地认为DGEMM效率会随着计算规模的不断减小计算量随之减小,直到降到很小,难以发挥硬件的计算能力。由于矩阵操作是一个三次方增长的,则HPL单步效率曲线是其在每步Δt时间内的积分值,累积效率曲线则是其在整个测试时间上的积分值,因此,HPL的单步效率曲线和累积效率曲线将分别有一个四次方和五次方的增量趋势,则式2变为：

（5）

η_{T \max} \geq η_{\max} = η_{DGEMM} (1 - {αx}^{4})

其中

x

为计算进度的百分比。

假设加速卡DGEMM的综合使用效率为86%,由于单节点没有节点间的网络传输,数据传输的影响最小,因此,采用单节点的实测曲线与计算模型进行对比分析。

图1

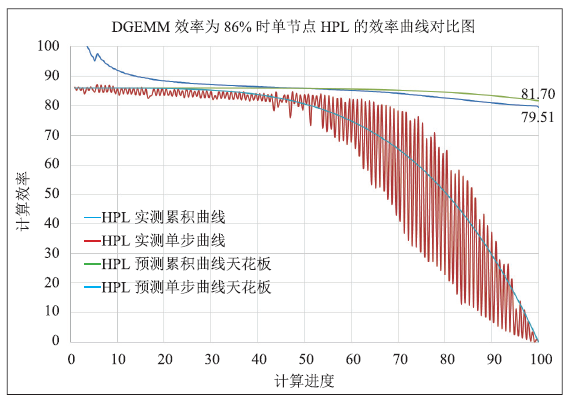
新窗口打开|下载原图ZIP|生成PPT
图1单节点HPL效率曲线的对比图

Fig. 1Contrast diagram of single-node HPL efficiency curve

通过图1中单节点的实测曲线与预测曲线可以看出,在不考虑网络影响的前提下,加速卡DGEMM的计算效率在一定程度上能够反映HPL的计算效率,尤其在HPL计算效率上限的对比分析中,由于忽略的PANEL分解和数据传输的影响,其预测结果也能够在很大程度上反映HPL计算效率的上限。

2.2 效率分析对比

超算系统HPL测试效率η,随着节点数的增加其效率有一定的降低,对HPL的主要影响因素的效率进行分析,主要表现在网络的通信随着节点的增多,通信方式越来越复杂,带来的开销也相应增加,在HPL的计算过程中,随着计算量的减小其开销逐渐体现在HPL的计算效率中。

超算系统计算能力与计算任务的均衡度η_s当系统完成后,针对不同的计算任务其是一固定的参数,可以针对相应问题通过分析和一定规模的测试获得;矩阵操作占整体HPL计算的比率η_MM为（2/3 N³-N²/2）/（2/3 N³+3/2 N²）;η_DGEMM为矩阵操作库函数的效率当前为86%;η_Lin为矩阵操作库函数的利用率95%;η_NET为网络传输对HPL数据传输性能影响效率,根据不同的通信算法η_NET的值也有不同,通过小规模测试发现,在4节点时,实测计算效率最高,本文以4节点实测效率80.01为基准进行预测分析,选

1 - \frac{\sqrt[]{|{lb ? lb (P * Q)}^{2} - 4|}}{100}

为η_NET的值,预测结果与实测结果对比如表1。

Table 1
表1
表1效率分析模型预测结果与实测结果
Table 1Prediction results and measurement results by the efficiency analysis model

节点数	N	P×Q	实测效率	预测效率	误差
2	124928	2×4	78.24	78.62	-0.38
4	176640	4×4	80.01	80.01	0
8	249856	4×8	78.03	78.22	-0.19
16	353280	8×8	77.69	77.24	0.45
32	499712	8×16	76.23	76.34	-0.11
64	706560	16×16	74.89	75.48	-0.59
128	999424	16×32	73.67	74.64	-0.97
256	1376256	32×32	73.72	73.81	-0.09
1024	2752512	64×64	72.01	72.17	-0.16

新窗口打开|下载CSV

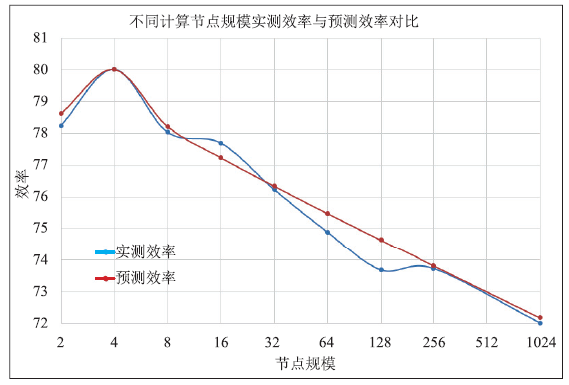
将表1中数据用图表示如图2。

图2

新窗口打开|下载原图ZIP|生成PPT
图2效率分析模型预测结果与实测结果对比图

Fig. 2Contrast diagram of prediction results and measurement results by efficiency analysis model

基于HPL测试计算规模增加计算效率有一定提高的特点,以及计算规模、计算能力、机器访存和网络传输等基本因素,在节点为4时达到计算效率的最高点,可以反映在当前优化方法的前提下,计算时间与数据传输时间匹配度较高,能够很好的发挥机器的计算能力。基于4节点实测结果,对其他节点进行分析预测,从图2中可以看出预测结果和实测结果吻合较好,说明该方法是能够在一定程度上反映超算系统的计算效率的。

2.3 多参数计算分析对比

HPL性能的影响因素主要涉及处理器性能、加速卡性能、库函数计算效率、网络带宽、延迟等参数,以及并行优化技术的效率等多方面因素。通过前文分析,在HPL测试中矩阵操作库函数的效率约为82%,网络是200Gb的infiniband,假设HPL计算过程达到70%后,计算时间便难以掩盖通信时间,以及并行传输优化方法提高传输效率,预测结果与实测结果对比如表2。

Table 2
表2
表2多参数分析模型预测结果与实测结果
Table 2Prediction results and measurement results by the multi-parameter analysis model

节点数	N	P×Q	实测效率	预测效率	误差
2	124928	2×4	78.24	81.81	-3.57
4	176640	4×4	80.01	81.72	-1.71
8	249856	4×8	78.03	81.37	-3.34
16	353280	8×8	77.69	81.07	-3.38
32	499712	8×16	76.23	80.62	-4.39
64	706560	16×16	74.89	79.89	-5.00
128	999424	16×32	73.67	79.04	-5.37
256	1376256	32×32	73.72	77.52	-3.80
1024	2752512	64×64	72.01	72.87	-0.86

新窗口打开|下载CSV

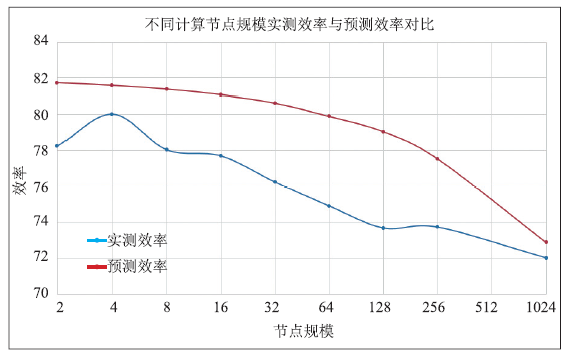
通过多参数计算预测HPL的效率,从图3中可以看出,预测计算效率随着计算规模、节点规模的增加,效率逐渐降低,为一光滑的下降曲线。由于多参数预测模型考虑因素有限,整体预测结果都略大于实测结果,尤其在节点规模为128的情况时,偏大超过了5%,可以很明显的发现,模型还不能够很好地反映P≠Q的情况,对计算效率的影响。在P=Q的情况下,整体预测结果误差不大于5%。

图3

新窗口打开|下载原图ZIP|生成PPT
图3多参数分析模型预测结果与实测结果对比图

Fig. 3Contrast diagram of prediction results and measurement results by multi-parameter analysis model

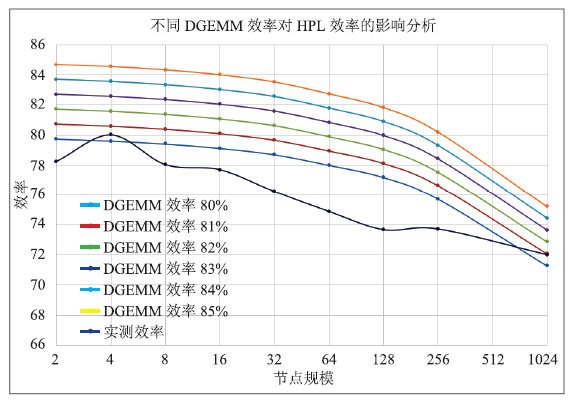
图4中显示了通过模型预测的HPL效率随DGEMM效率的变化规律,图中DGEMM的效率从80%提升到85%,HPL的效率也从71.3%提升到75.2%,HPL计算效率随着DGEMM效率的增加,各节点规模HPL效率的增加量随DGEMM的效率基本成线性增加,预测结果也很好的反映了通过提高DGEMM效率能够提高HPL效率的基本规律。

图4

新窗口打开|下载原图ZIP|生成PPT
图4不同DGEMM效率对HPL效率的影响

Fig.4Effect of different DGEMM efficiency for HPL efficiency

3 结论

本文针对HPL性能预测的不同需求,分析了影响HPL效率的主要因素,分别建立了HPL计算效率上限、多因素对HPL效率影响的并行计算模型,分析结果与实测结果进行了对比,两者吻合较好。通过分析与验证等到了以下相关规律：

（1）超算系统中,HPL效率的上限主要取决于超算系统主要计算部件的库函数DGEMM的性能;

（2）在大规模超算系统HPL测试中,计算任务均衡度、库函数效率、库函数在计算中的比率、库函数利用率、网络利用率等影响HPL效率的主要因素,在一定程度上能够反映该超算系统HPL的计算效率;

（3）在大规模超算系统中DGEMM的效率与HPL的效率成正比,DGEMM库函数效率的提高,HPL计算效率也有相应的提升。

4 展望

HPL的并行计算模型研究与计算系统密切相关,尤其是当前强异构的复杂超算系统,随着节点规模的增加,HPL测试成功的几率也随之降低。在上万节点的规模的测试中,每进行3~5次测试,才可能会有一次成功结果,致使当前大规模HPL测试中超算系统的可靠性和稳定性是决定HPL测试成功与否的关键因素。如何基于E级超算系统,建立能够反映其通信容错能力、系统稳定性、系统压力承受程度、程序计算需求的不均衡性与系统的适应度等欠稳定特性的并行计算模型,还是一个新的问题。

致谢

在此，感谢测试团队尽职尽责昼夜奋战在系统测试一线，为计算模型的研究工作提供了大量宝贵数据。同时也感谢中国科学院计算技术研究所谭光明研究团队与我们在该项目中的相互交流。

利益冲突声明

所有作者声明不存在利益冲突关系。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Top500 Organization. Supercomputer rank list
[EB/OL]. 2019 -11-20. .

URL [本文引用: 1]

[2]

Top100 Organization. Supercomputer rank list
[EB/OL]. 2018- 10- 20. .

URL [本文引用: 1]

[3]

Dongarra J

, Luszczek

, Petitet

. The LINPACK benchmark: Past, present and future
[J]. Concurrency and Computation: Practice and Experience, 2003,15(9):803-820.

[本文引用: 1]

[4]

罗水华, 杨广文, 张林波, 石威, 郑纬民 . 并行集群系统的LINPACK性能测试分析
[J]. 数值计算与计算机应用, 2003, ( 4):285-292.

[本文引用: 1]

[5]

张文力, 陈明宇, 樊建平 . HPL 测试性能仿真与预测
[J]. 计算机研究与发展, 2006,43(3):557-562.

[本文引用: 1]

[6]

Wang

, Yang

, Du

, Chen

, Yi

, Xu

. Optimizing linpack benchmark on GPU-accelerated petascale supercomputer
[J]. Journal of Computer Science and Technology. 2011,26(5):854-865.

[本文引用: 1]

[7]

Wang

, Yang

, Du

, Chen

, Yi

, Xu

. Optimizing linpack benchmark on GPU-accelerated petascale supercomputer
[J]. Journal of Computer Science and Technology 2011,26(5):854-865.

[本文引用: 1]

[8]

王申, 漆锋滨, 谷洪峰, 潘治 . LINPACK 并行性能模型及其预测
[J]. 计算机工程, 2012,38(16):81-84.

[本文引用: 1]

[9]

Cabrera

, Almeida

, Blanco

, Giménez

. Analytical modeling of the energy consumption for the High Performance Linpack
[C]. 21st Euromicro International Conference on Parallel, Distributed, and Network-Based Processing, 2013: 343-350.

[本文引用: 2]

[10]

贾迅, 邬贵明, 谢向辉 . 异构高性能计算系统Linpack效率受限因素分析
[J]. 计算机工程与科学, 2018,40(2):224-230.

[本文引用: 1]

[11]

甘新标, 孙燎原, 刘杰, 雄成伟, 黄嘉昆 . 面向国产异构系统的HPL异构协同设计
[J]. 计算机工程与科学, 2018,40(1):10-14.

[本文引用: 1]

[12]

Gan

, Hu

, Liu

, Chi

, Xu

, Gong

, Li

, Yan

. Customizing the HPL for China accelerator
[J]. 2018, 61:042102:1-042102:11.

[本文引用: 1]

[13]

Kindratenko

, Trancoso

. Trends in high-performance computing
[J]. Computing in Science & Engineering, 2011,13(3):92-95.

[本文引用: 1]