 ,*清华大学计算机科学与技术系,北京 100084
,*清华大学计算机科学与技术系,北京 100084COS: Measuring the Efficiency of Distributed Big Data Processing System
Li Xiaohan, Chen Wenguang ,*Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China
,*Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China通讯作者: * 陈文光(E-mail:cwg@tsinghua.edu.cn)
收稿日期:2019-10-28网络出版日期:2020-02-20
Received:2019-10-28Online:2020-02-20
作者简介 About authors

李晓涵 ,清华大学计算机系高性能计算研究所,研究生,主要研究方向为大数据处理、并行程序设计。
主要贡献:完成单机程序实现、分布式系统性能测试、论文撰写等工作。
Li Xiaohan is currently a Master student of Institute of High-Performance Computing, Department of Computer Science and Technology, Tsinghua University. Her research interests are big data processing and parallel programming.
Undertaking the following tasks in this article: Algorithm implementation, experiments on clusters, and article writing.
E-mail: xh-li18@mails.tsinghua.edu.cn

陈文光 ,清华大学计算机系,教授,主要研究方向为并行计算和分布式系统。
主要贡献:在指标设计、论文组织等方面给予建设性指导。
Chen Wenguang is a Professor in Department of Computer Science and Technology, Tsinghua University. His research interests are parallel computing and distributed systems.
Undertaking the following tasks in this article: Supervising on metric design and article organization.E-mail:cwg@tsinghua.edu.cn

摘要
【目的】在大数据处理领域,分布式计算系统得到广泛应用,它们的可扩展性得到重点关注,但其绝对性能往往没有得到重视。我们希望提出科学合理、与时俱进的度量标准,对分布式系统的性能进行评估。【方法】本文通过对比特定任务的单机实现和分布式实现来讨论分布式系统的性能,提出COS(Configuration that Outperforms a Single machine)这一指标,来衡量分布式系统在达到单台机器的性能时,需要的硬件资源数量。我们选取k-means聚类和逻辑回归两个经典机器学习算法,对其进行单机多线程实现,并通过向量化计算、优化内存分配与访问等方式对性能进行了优化,为分布式多机系统的性能提供参考。【结果】以Apache Spark作为对标系统,实验发现无论是使用其原生编程接口,还是经过悉心优化的机器学习库,都要使用数倍甚至数百倍的机器,才能达到单机多线程实现的性能。【局限】分布式系统与单机实现进行性能对比并不是完全公平的,分布式系统的额外开销客观存在。【结论】但COS指标仍能反映分布式系统存在的绝对性能较差、没有充分利用硬件优势等问题。
关键词:
Abstract
[Objective] Distributed computing systems are used widely in the field of big data processing. They are designed and implemented with a focus on scalability. With good scalability, a system can hold and process a growing amount of data by adding resources without modifying the system itself while sacrificing the absolute performance of a single machine at huge expenses. We want to offer a reasonable and modern metric to evaluate the performance of distributed systems. [Methods] In this article, we discuss the performance of distributed systems by comparing them with the same task on a single machine with the proposed metric, COS, or the Configuration that Outperforms a Single machine. The COS of a system on a given problem is the number of machines required when the system outperforms a competent single-machine implementation. Given a limited hardware resources, COS of a distributed system is usually too large to measure. So, we offer another metric by giving a parameter n to COS. COS(n) equals to n multiplied by the time used on n machines over that on a single machine. COS(n) indicates the performance and expense loss in a cluster system. We implemented two classic machine learning algorithms, k-means clustering and logistic regression, on a single machine with multi-threading, SIMD support and NUMA-aware memory control. [Results] Our experiments show that by using Apache Spark, with no matter its native API or optimized machine learning library like MLlib, it needs tens to hundreds of machines to achieve the same performance as we did on a single machine. [Limitations] The comparison between a single machine and a cluster is not entirely fair, for overheads in a cluster is unavoidable. [Conclusions] This COS metric can still reflect the problems of poor absolute performance and insufficient utilization of hardware advantages in distributed systems.
Keywords:
PDF (8420KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李晓涵, 陈文光. COS:度量分布式大数据处理系统的效率. 数据与计算发展前沿[J], 2020, 2(1): 93-104 doi:10.11871/jfdc.issn.2096-742X.2020.01.008
Li Xiaohan.
引言
随着互联网时代海量数据的产生,许多分布式计算系统应用在图计算、机器学习等各种大数据处理任务上,例如常见的Hadoop[1]、Spark[2]等等,它们是用多台多核机器搭建起来的,对于这样的系统,人们非常关注它们的可扩展性,即系统面对的任务规模变大时,能不能通过增加硬件的方式,实现性能的线性增长。在这一方面,已经有大量的工作和研究,但可扩展性得到关注的同时,系统的实际性能往往没有得到很好的优化。人们应当关注,在使用了多机多核的情况下,分布式系统到底达到了什么等级的性能提升,甚至是导致了什么等级的性能下降。Frank McSherry等人发表的论文《Scalability! But at what COST?》[3]关注了这个问题,该论文提出“COST”这一指标,即“Configuration that Outperforms a Single Thread”。对于一个计算系统来说,它的COST指标指的是,使用相同的算法和数据,其运行速度与单线程实现的运行速度相当时所用的配置。论文的作者分别使用Rust和C#语言实现了PageRank、Union-Find、Label propagation等算法,在Twitter和uk-2007这一大一小两个数据集上进行测试,并与其他系统报告出来的在这两个数据集上做的同样算法的测试进行了比较。结果显示,Naiad、GraphX、GraphLab等系统,常常需要几十上百个核,才能达到优化后的单核实现的性能。这是值得分布式计算系统的设计者思考的。
传统计算机只使用一个处理器来完成计算任务,现在,多核处理器已经成为主流,单台机器已经具备了强大的并行能力,如果经过精心的设计和实现,单台机器上能达到的性能,与一定规模的分布式系统能达到的性能相当。今天再来考虑对多机系统的性能进行评估的问题,可以提出一个新的角度:在使用了多机多核的情况下,与单机多核相比,分布式系统到底达到了什么等级的性能提升,甚至是导致了什么等级的性能下降。这是本文主要关注的问题。为此,本文提出了COS和COS(n) 两个指标,用以衡量分布式系统的整体和实际开销。
本文选择进行评估的系统是Apache Spark,一个在工业界得到广泛应用的分布式系统,该系统在Hadoop基础上对数据对象进行了优化,提出了Resilient Distributed Dataset(RDD)的概念[4],性能比Hadoop系统得到了很大提升。中国科学院推出的开源基准测试套件BigDataBench[5],提供13个来自真实应用的数据集,并为47个不同类型的算法提供了性能基准。得益于这个工作,我们可以得到具有参考价值的Spark系统的性能情况。
此外,Spark的开发人员还针对机器学习应用,提供了MLlib编程库[6],对诸多标准学习算法提供了高效可扩展的编程实现。MLlib在垃圾回收、多机通信、负载均衡等数个方面实现了性能提升,并根据算法特点进行了针对性优化,在底层调用C++的线性代数库,大大提高线性代数方面的计算效率。
1 研究方法
本文首先定义指标COS (Configuration that Outperforms a Single machine)。一个分布式系统的COS,即使用相同的算法和数据,其运行速度与单机多线程实现的运行速度相当时,所使用的机器数量。为测量一个系统的COS值,先选定算法和对应的数据,精心实现其单机多线程版本,获得运行时间的数值,然后使用同样的算法和数据,在分布式系统上进行测试。若要得到准确的COS值,应不断增加集群中的机器数量,直到在分布式系统上的运行时间达到(或少于)单机版本。由于同步、通信、容错等开销的存在,以及设计上的不足,分布式系统的COS值通常会很大,对于某些系统来说甚至有可能是正无穷,实际投入如此规模的集群进行测试是不可行的,测量准确的COS值也是不现实的。因此,我们为COS增加参数n,COS(n) 的计算方式是:
当n台机器用时与单机用时基本相当时,COS(n) 即为我们最初定义的COS值。
COS反映的是一个系统的整体效率,COS(n) 则能反映分布式系统在不同规模下的表现,因而具有更实际的参考价值。COS(n) 计算公式的分子部分,与一个计算任务的经济成本是成正比的(想象用户租借n台云服务器来完成这个任务),因此,COS(n) 代表着一个特定计算任务,在n台机器构成的集群上完成需要花费的代价倍数,这对于性价比敏感的用户来说,可以作为一个非常重要的参考。
本文的实验部分,选取了k-means聚类和逻辑回归两个经典机器学习算法,对其进行单机多线程实现和优化,并以此为基础,对Apache Spark系统进行评估。两个算法都需要迭代计算,因此,我们将单轮迭代用时作为计算COS和COS(n)时的时间数据,以消除系统初始化、数据预处理等环节对评估的影响。希望通过这项工作,为考察分布式多机系统的性能提供一个新的视角。
2 k-means聚类算法的实现与优化
2.1 算法并行化概述
聚类算法是一种无监督学习的经典方法。聚类算法的每个样本可由一个向量表示,代表着高维空间中的一个点的坐标,算法通过把样本点划分成不相交的子集(每个子集称为一“簇”),来揭示数据之间的内在规律,达到分类的目的。聚类算法中最经典、最常用的是k-means聚类算法,k代表的是簇的个数,means说明了簇的中心以取簇内样本均值的方式计算。k-means算法通过多轮迭代,将样本划分到不同的簇中,最终目标是最小化簇内样本相对中心的平方误差,实际应用中往往通过限制迭代轮数来逼近目标,得到近似解。k-means算法作为一种基于距离计算的算法,在用户画像、商品推荐、影视作品分类等方面有较多应用。2.2 算法优化
2.2.1 数据与平台为了评估单机多线程k-means算法的性能,及各种优化手段达到的效果,本论文后续性能报告均基于一个含有80,000,000个样本,每个样本维度为64的数据集。该数据集原数据来自BigDataBench,其测试套件中的脚本能生成9维k-means数据,考虑9维维度较低,且数据无实际意义,故将数据重新分割为64维。实验中可能对数据做文本文件和二进制的转换,以获得较快的读取速度。若无特殊说明,则实验时一般取k=500,报告数值为10轮迭代的迭代时间平均值。
本节汇报的性能数据,基于的处理器配置为:Intel(R) Xeon(R) CPU E7-8890 v3 @2.50GHz,有4个socket共72个核。
2.2.2 Reduction
在为每个样本计算距离最近的中心点时,需要同时记录每个中心点代表的子集中拥有的样本个数,通过一个数组来维护这个值,此时会出现数据竞争的现象,即同一时刻可能有不同的线程需要写同一个值,为了保证正确性,可以通过加锁或原子操作来进行,这两种做法都会将写入变成串行,且加锁还需要额外的内存和时间开销。针对类似的需求,OpenMP提供了这样的编译指导子句:reduction。该操作指的是,每个线程先保存数据的一份副本并进行维护,在线程工作结束后,统一将所有线程的数据按照某种运算规则进行合并。计算过程中,各线程之间数据相互独立,避免了数据冲突,在k-means的迭代过程中应用,可以使性能得到很大提升。
2.2.3 并行对象选择
在重新计算中心点时,有三种并行策略可以选择:按样本并行、按中心点并行、按维度并行,三种策略都有自己的缺点:
样本并行:修改中心点的操作会有数据竞争,需要加锁,影响并行度,并且有额外开销。可以通过reduction操作进行优化。
中心点并行:线程负载非常不平衡,可以通过调度策略进行一定的优化。在k较小时,并行度较低。
维度并行:在维度较低时,并行度较低。维度并行时跳跃访问原数据,对cache非常不友好。
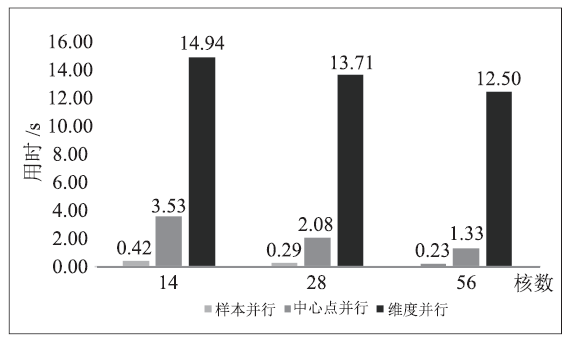
针对以上三种并行策略,考察重新计算中心点需要的时间,进行了实验。从图1可以看出,对于中心点重新计算这项任务,不管是以哪种方式并行,其加速比都很差。这是符合预期的,因为每一种并行方式的计算过程中都有额外开销或负载不均衡等影响并行度的因素。三种方式中,按照样本并行,并采用reduction操作,速度最快,能达到维度并行速度的数十倍。这两种并行策略相比,维度并行没有很好地利用cache,从而对性能造成了灾难性影响,这启示我们,高效利用cache是提高程序性能的有效手段。按照中心点并行,对样本点的访存也有很大概率是随机的,也存在cache利用率低的问题。
图 1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图 1三种并行方式迭代用时
Fig.1Iteration time of different parallel strategies
2.2.4 距离的等价算法
设有d维样本点X与某子集中心点C,有如下等式:
$distance(X,C) \\ =||X-C]]^2 \\ =\sum_{i=i}^d(X[i]-C[i])^2 \\ =\sum_{i=1}^dX[i]^2+\sum_{i=1}^dC[i]^2-2(\sum_{i=1}^dX[i]*C[i]) $
其中X[i]代表样本点X的第i维数值。
观察展开后的公式,其中$\sum_{i=1}^dX[i]^2$只与样本点有关,因此可以在整个算法开始时计算并保存,$\sum_{i=1}^dC[i]^2$只与子集中心点有关,因此可以在每次迭代开始即中心点发生改变时,计算并保存。通过提前计算,一轮迭代可以大概节约n*k*d次减法运算。带来了约11%的性能提升。
2.2.5 下限判断法
在朴素的k-means做法中,对于一个样本点来说,需要遍历所有子集的中心点,维护一个欧氏距离的最小值,从而找到离自己最近的一个。设X与C为实数向量,柯西-施瓦茨不等式告诉我们:
将不等式带入距离公式,有:
$distance(X,C) \\ =||X-C]]^2 \\ =\sum_{i=i}^d(X[i]-C[i])^2 \\ =\sum_{i=1}^dX[i]^2+\sum_{i=1}^dC[i]^2-2(\sum_{i=1}^dX[i]*C[i]) \\ \ge\sum\limits_{i=1}^dX[i]^2+\sum\limits_{i=1}^dC[i]^2-2\sqrt{(\sum\limits^d_{i=1}X[i]^2)*(\sum\limits^d_{i=1}C[i]^2)} \\ =(\sqrt{\sum\limits^d_{i=1}X[i]^2}-\sqrt{\sum\limits^d_{i=1}C[i]^2})$
这个不等式中$(\sqrt{\sum^d_{i=1}X[i]^2}-\sqrt{\sum^d_{i=1}C[i]^2})^2$这一部分,是两个向量之间距离的一个下限,其中$\sqrt{\sum^d_{i=1}X[i]^2}$只与样本点有关,因此可以在整个算法开始时计算并保存,$\sqrt{\sum^d_{i=1}C[i]^2}$只与子集中心点有关,因此可以在每次迭代开始即中心点发生改变时,计算并保存。因此,距离下限的计算只需要2次访存、1次减法、1次乘法。在寻找样本及其最近的中心点时,则可以先通过非常小的计算开销获得样本点与当前中心点距离的下限,当前最小距离与下限进行比较,若小于,则不用继续计算距离。将这一策略称为下限判断法。
经过测试,在当前数据集上,下限判断法能够避免约35%的向量距离计算,但对性能的提升不到10%。经过分析,可能的原因有两个:一是下限判断法引入了条件判断的分支,而分支预测错误会导致时钟周期的浪费;二是下限判断法导致访存不连续,Cache的频繁换入换出使得实际的性能提升没有那么显著。
3 逻辑回归算法的实现与优化
3.1 算法并行化概述
逻辑回归模型是一个广义的线性回归统计学模型,逻辑回归算法是应用逻辑回归模型到数据集,通过迭代优化求解回归参数的算法。逻辑回归虽然被叫做“回归”,但通常用来解决二分类问题,是一个分类算法。对于一个向量表示的样本点,我们熟悉的线性回归模型,其拟合后的输出是连续的数值,而逻辑回归则希望拟合后的最终输出能代表该样本被分为某一类的概率,从而完成分类问题。假设在一个二分类问题中,正负例的标签y分别用1和0表示,数据用x表示,有d-1维向量表示的样本点$X_i$,我们希望其被分为正例的概率P(y=1|x=X_i)$能够用一个的函数来表示:
$P(y=1|x=X_i)=\frac{e^{w\cdot X_i}}{1+e^{w\cdot X_i}}=\frac{1}{1-e^{-w\cdot X_i}}=h_w(X_i)$
其中w为权值向量。逻辑回归算法即使用极大似然思想和梯度下降的方法,通过已知的样本训练求出w,带入到$h_w(X_i)$对未知样本进行预测。篇幅所限,省略推导过程,梯度下降的权值更新公式为:
$w[j]=w[j]-\frac{\alpha}{m}\sum\limits_{i=1}^n(h_w(X_i)-Y_i)X_i[j]$
其中m为推导中引入的任一正实数,α为梯度下降的幅度参数。设所有样本组成矩阵X,所有标签组成向量Y,则梯度下降的过程可以用线性代数的矩阵和向量计算表示为:
$w=w-\frac{\alpha}{m}X^T(h_w(X)-Y)$
采用梯度下降法求解逻辑回归的权值向量,可以转化为若干步矩阵和向量运算。而向量运算的并行化思想是天然的,例如矩阵乘以向量时可以按行并行,向量之间相减时可以按元素并行,还可以采用单指令多数据(SIMD)思想进行优化等等。也可以通过样本并行,不按照向量化思想,而是对于每个样本单独计算,最后将各个样本对梯度下降的贡献合并。
3.2 算法优化
3.2.1 数据与平台为评估单机多线程版本的逻辑回归算法的正确性和性能,避免算法过早收敛,选择MNIST手写数据集[7]中的0和1的部分,共12 665个样本,样本的维度是784。以此作为基本数据集,将其重复1000倍,得到一个规模较大的数据集,以方便性能的测试。若无特殊说明,则实验时一般使用所有处理核心,进行10轮梯度下降过程的迭代,报告数值为10轮迭代的迭代时间平均值。
本节汇报的性能数据,基于的处理器配置为:Intel(R) Xeon(R) CPU E7-8890 v3 @2.50GHz,有4个socket共72个核。
3.2.2 应用Intel Math Kernel Library
为了在多核和多处理器系统上获得最佳性能,程序需要充分利用并行性的特点,有效地管理存储器层次结构的特征。英特尔数学内核库(Intel MKL)[8]旨在帮助程序员利用多核、多处理器或集群的高性能计算优势,它支持一系列优化和线程化的数学功能,以充分利用英特尔处理器的潜能。第一次调用函数时,MKL会启动运行时检查,以了解要使用的硬件。根据检查结果,MKL选择合适的函数来利用指令级和寄存器级SIMD并行性。英特尔MKL还集成了线程安全功能,并且做了很好的负载均衡。
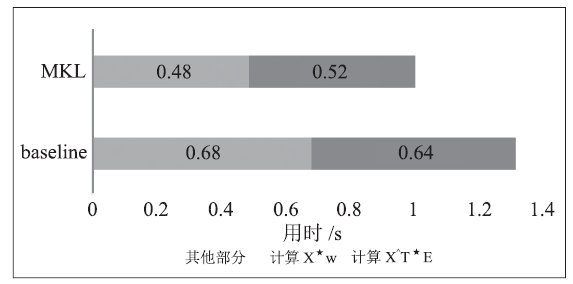
将逻辑回归的梯度下降过程归纳为线性代数计算形式后,可以采用MKL提供的接口cblas_sgemv与cblas_saxpy,完成矩阵-向量运算和向量-常数运算。作为对比,先实现了朴素的矩阵计算形式,并对转置矩阵乘的计算进行了优化,保证样本矩阵每行按顺序访存,以充分利用缓存。从图2可以看出,MKL通过对硬件的充分利用,获得了25%至30%的性能提升。
图 2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图 2应用MKL带来的性能提升
Fig.2Performance improvement with MKL
3.2.3 访存优化
使用MKL虽然获得了一些性能提升,但发现在扩展到多核的情况下,其加速比是较差的。通过性能分析,发现程序在线程数较多的时候,计算能力较强,而访存成为了瓶颈。因此,想要进一步优化程序,必须考虑减少访存,或增加访存的局部性。
按照线性代数形式进行计算,需要进行两次矩阵-向量乘,这是整个程序耗时最多的部分,而两次计算都要将样本矩阵X遍历一遍。受分布式逻辑回归的启发,可以将两次对同一样本的遍历调整到一起进行,这样虽然不能采用向量化的计算形式,但是可以更好地利用缓存。通过这种优化,单线程用时在MKL的版本上减少了25%,整体用时减少了40%左右,且加速比得到进一步提升。
3.2.4 NUMA绑定
虽然访存优化后,性能有所提升,但是加速比仍然不理想,该程序仍然存在访存瓶颈。进一步提升访存速度,则需要考虑处理器的存储架构。本文涉及到的单机多处理器系统采用非统一内存访问架构(NUMA)[9],在这种架构下,单机系统中不同的处理器会被分配在不同的NUMA节点上,访问自己所在的NUMA节点的内存,会比访问其他节点或共享内存更快一些。例如,在当前所用的服务器上,有4个NUMA节点,使用Intel Memory Latency Checker测得NUMA内访存带宽约为70.7GB/s,而跨NUMA节点的访存带宽约为14.2GB/s。在逻辑回归算法中,主要的存储和访存开销是样本数据,而且根据2.2.3中提到的每个样本只遍历一次的策略,一个线程可以只访问部分数据点,那么考虑将数据分散存储在不同的NUMA节点上,该节点的线程只访问自己节点的数据,将能够提升程序性能。
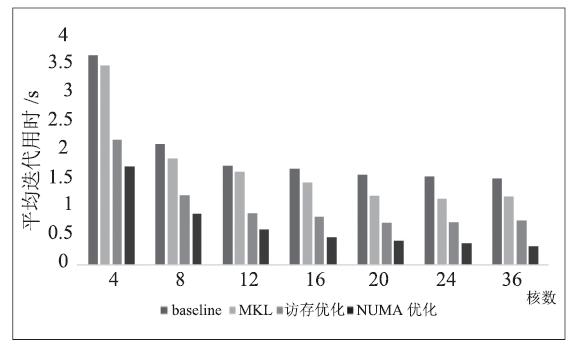
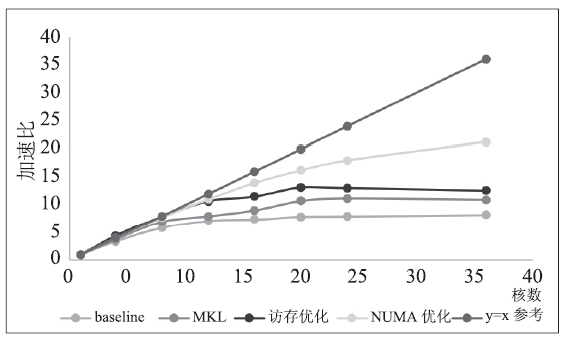
为实现线程和内存与NUMA节点的绑定,采取MPI进程的方式,每个进程分配一部分数据,并将进程绑定在NUMA节点上。本节测试环境有4个NUMA节点,每个节点含18个核。由于测试数据较大,单NUMA节点并不能完全装下,故不测试单核(单线程)性能,4核加速比按照4来计算。图3和图4显示,在绑定NUMA节点后,迭代用时减少30%-50%,且加速比有较好提升,说明访存瓶颈得到了缓解。
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3逻辑回归性能
Fig.3Performance of Logistic Regression
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4逻辑回归加速比
Fig.4Speedup of Logistic Regression
4 性能测试与分析
4.1 测试背景
Table 1表 1
表 1测试环境
Table 1
| 项目 | 详情 |
|---|---|
| 节点数 | 4 |
| 节点型号 | Intel(R) Xeon(R) CPU E5-2680 v4 @2.40GHz |
| 单机核数 | 28 |
| Spark版本 | 2.2.0 |
| 通信 | 千兆以太网 |
新窗口打开|下载CSV
4.2 k-means聚类算法
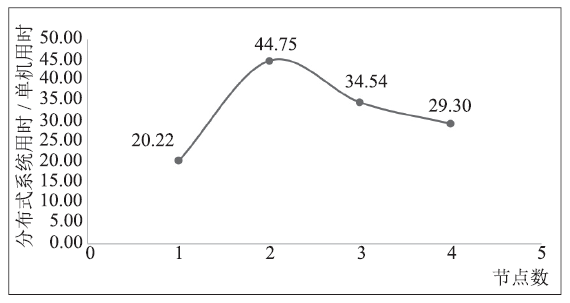
4.2.1 BigDataBench k-meansBigDataBench[5]是中国科学院计算技术研究所提供的基准测试套件,该套件实现的k-means算法是完全基于Spark提供的通用接口的,与未经快速距离计算、下限判断法优化的k-means算法是等价算法。性能情况如图5。
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5原生Spark API k-means性能
Fig.5Performance of k-means with Spark API
从图中可以看出,BigDataBench版本的k-means代表的是采用原生Spark接口实现的k-means性能,显著特点是,在机器较少的时候,性能甚至不如Spark的单机版本,这说明其通信开销巨大。
4.2.2 MLib k-means
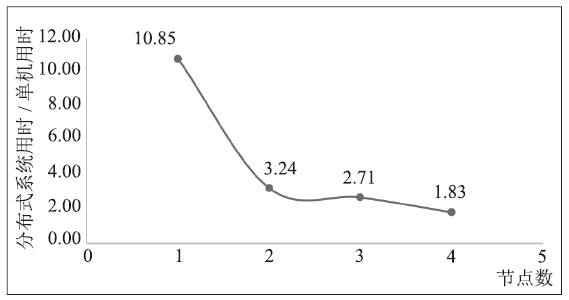
MLlib中的k-means也使用了快速距离计算、下限判断法进行优化,它与同样使用这些优化的k-means算法是等价算法。调用MLlib库中提供的k-means算法接口,测得性能与单机性能的比值如图6。
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6MLlib k-means性能
Fig. 6Performance of k-means with MLlib
MLlib作为Spark开发团队的作品,比起用原生Spark来实现的算法,其性能提升是巨大的。它在单节点上较差的性能,说明其确实针对分布式应用做了许多优化。底层调用C++科学计算库,也一定程度上缓解了Scala语言速度慢的问题。与原生接口的版本相比,其运行速度提高了数十倍,这说明Spark确实有极大的优化空间,这种优化需要对系统的深入认识,和对算法的针对性实现来进行,因而需要较高的开发门槛。
4.3 逻辑回归算法
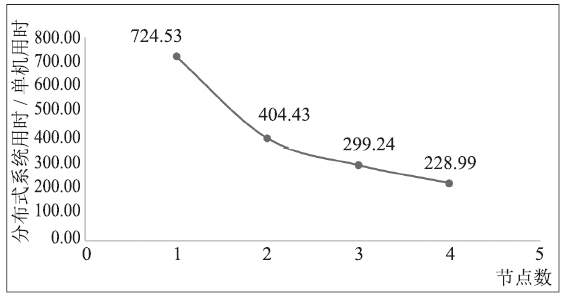
4.3.1 原生 Spark API逻辑回归BigDataBench中并未包含逻辑回归算法,因此,我们基于Spark的map、reduce等原生接口,对逻辑回归算法进行了实现。由图7可以看出,这种实现的扩展性趋势较为明显,但绝对性能依然较差,每轮迭代都要花费数百倍于单机的时间。
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7原生Spark API逻辑回归性能
Fig.7Performance of Logistic Regression with Spark API
逻辑回归作为一个需要大量向量计算的算法,较快的编程语言(C/C++)、SIMD等单机优化手段对其性能的提升非常关键,原生Spark API的实现性能较差是可以理解的。MLlib针对线性代数计算进行优化之后,性能提升也是非常明显的。
4.3.2 MLlib 逻辑回归
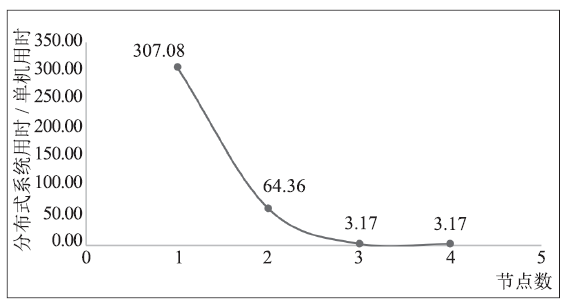
MLlib中实现了基于有限内存BFGS方法[10]的逻辑回归和基于随机梯度下降的逻辑回归。随机梯度下降法,即在计算每一次梯度下降时,只取一部分样本进行计算,以提高计算效率。为与本文实现的梯度下降法进行对比,将每次随机梯度下降选择的样本比例设置为100%,进行测试,Spark集群性能对比如图8。
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8MLlib逻辑回归性能
Fig.8Performance of Logistic Regression with MLlib
同k-means算法的情况类似,MLlib在单节点上性能较差。从图8观察,前3个数据点加速比超过了机器数,有可能与数据存储有关,数据分布在多台机器上时,单台机器上数据规模减小,可能能够存入更高速的存储层级。第3、4个数据点性能几乎相同,猜测与通信特性有关,在经过良好的计算优化后,通信有可能成为程序运行的瓶颈。
4.4 COS(n)
根据测得数据,计算系统的COS(n)。在不同算法和配置下,COS(n)的具体数值和变化趋势也不同,这与具体的计算和通信特性有关。COS(n)的具体数值从几到数百不等,这反映了分布式系统需要花费数倍甚至数百倍的代价去完成一个计算任务。分布式系统的设计者应当关注好这一问题,在系统设计和实现方面充分考虑实际性能开销,在系统评估时选取更具有参考价值的基准。
Table 2
表 2
表 2COS(n)
Table 2
| Apache Spark | MLlib | |||
|---|---|---|---|---|
| n | k-means | 逻辑回归 | k-means | 逻辑回归 |
| 1 | 20.22 | 724.53 | 10.85 | 307.08 |
| 2 | 89.50 | 808.85 | 6.49 | 128.72 |
| 3 | 103.63 | 897.71 | 8.12 | 9.51 |
| 4 | 117.18 | 915.94 | 7.32 | 12.69 |
新窗口打开|下载CSV
5 总结
5.1 提高并行程序性能的一般方法
本文的主要工作是实现了单机多线程版本的k-means聚类算法和逻辑回归算法,对其性能进行了优化和测试,并与Spark系统进行了对比。在优化单机多线程程序的过程中,有许多方面的优化对性能的影响是明显的,总结在本节。CPU运算能力提升很快,但访存速度的提升则相对缓慢,许多程序在现代处理器上运行的瓶颈是访存。针对访存瓶颈的应用程序,首先应当从算法运行的层面考虑能否减少访存,或者经过仔细设计,使得访存能更好地利用更快速的处理器。
CPU高速缓存(Cache)在存储器层次结构的金字塔中,仅次于寄存器,能够提供高速的读写,但是大小非常有限。在需要很多访存的程序中,提高Cache命中率,即提高内存访问的时间和空间局部性,是让程序拥有良好性能首先要考虑的事情。数据对齐对于减少Cache换入换出具有重要意义,想要获得好的性能,需要根据访存模式和Cache大小的特点进行仔细的数据和访存设计。此外,现代处理器大都支持SIMD(Single Instruction Multiple Data)技术,而SIMD的应用也对数据对齐有一定的要求。
使用了NUMA技术的同一个机器中,不同处理器核之间的访存也存在差异,合理分配数据和处理器,降低跨NUMA访问,会使访存性能更好,从而使整体性能得到提升。
数据竞争是多线程程序需要考虑的重要方面,它不仅可能带来程序正确性的问题,还会干扰访存、降低程序性能。因此,若内存允许的情况下,采用reduction操作代替锁或原子操作,是较好的选择。
此外,好的工具能够给优化过程带来很多帮助。多线程编程工具例如OpenMP,提供了线程调度等方面的支持,MKL等科学计算的库,已经很好地利用了硬件资源,且对于平台有很好的兼容,VTunes、perf等性能分析工具,能让我们从更系统的视角来观察程序的运行过程,为优化工作提供启发。
5.2 影响多机系统性能的原因分析
与单机系统相比,可扩展的分布式系统在设计和实现时,有许多方面会导致经常性开销的增加。特定系统的编程框架和计算框架限制了算法的表达。例如Map-Reduce模型,它具有很好的通用性,很多算法能够用它来表达,但是任务之间的独立性和切换的开销不利于高效的实现。而且它为了保持可扩展性,不支持内存驻留状态,因此任务之间的数据共用依赖于HDFS,增加了数据备份、写入和读取以及序列化的开销。Pregel[11]和HaLoop[12]都是针对迭代计算的数据重用进行了优化的系统,但它们支持的计算模式也都比较局限。Spark的RDD模型支持内存计算[13]和数据重用,相对原始的MapReduce模型来说是一个很大的提升,但其编程模型仍然具有局限性,当应用程序需要支持细粒度的数据修改时,Spark需要经过对RDD的拆分和重新包装,这无疑会带来时间和空间的双重开销。为了保持大数据系统的可扩展性,其应用就被限制在了天然并行的那些模型。但是这些模型可能并不符合程序员的原始意图,或者并不是一个算法最高效的并行实现。例如逻辑回归等机器学习算法,运用SIMD技术或矩阵运算的针对性优化,能达到很好的性能提升,但这是RDD所难以做到的。
分布式系统中,不同机器节点之间的通信是最常见的开销之一。目前,有许多技术能够提升通信带宽,例如InfiniBand[14]、RDMA[15]等,也有很多工作针对特定应用的分布式通信做了相当多的优化,例如针对图计算系统的Gemini[16],但与单机的天然共享内存相比,这个问题只能缓解,无法解决。同时,多机通信也是制约分布式系统可扩展性的重要因素,因为随着节点数线性增加,通信量的增加往往是平方甚至指数级别的。
分布式还会带来容错和一致性的问题。为了增加数据保持的容错性,需要采用备份等方式来存储数据,不同数据备份之间则需要通过复杂的协议来保证一致性,协议的运行所带来的计算和通信开销不可忽视。同时,为了应对计算过程中出现的正确性问题,有些系统采用Check Point的方式实现容错,以Spark为代表的系统则采用了Dryad[17]系统提出的DAG图的思路,用线性有序的图来记录数据和计算的过程。
分布式系统的实现方式,也有可能增加经常性开销。使用更高级的语言,比如Java、Scala,能够降低开发难度、提高开发速度,但是它们可能带来性能上的问题。基于JVM的语言,其垃圾回收、堆栈利用、内存管理和指令翻译等特性使得程序运行的开销增大,此外,JVM的包装使得它在与其他加速设备,例如GPU相结合时,必须经过开销极大的远程方法调用[18],或借用其他语言例如Python进行包装[19]。
分布式系统有其天然的开销需求,而特定系统的实现方式也会对性能造成伤害,但除了高性能计算领域外,很多其他领域的应用往往并不十分关注性能,除非性能对应用的可行与否有关键性影响。高扩展性的系统,使得用户可以通过增加硬件的方式,提高系统的处理能力,因而许多大数据系统选择了更容易使用的的开发语言,并且将可扩展性作为主要关注的指标,从一定程度上讲,这也是可以理解的。
5.3 未来工作
算法方面,k-means聚类算法还有一些更高效的实现方式,例如Lloyd算法[20]、Canopy k-means[21]等,它们与原算法虽然并不是等价算法,但是可以节约许多非必要计算,在许多对精确度要求并不高的场合,通常是可以接受的。逻辑回归算法也有其他的实现方式,例如使用牛顿法进行优化问题的求解。如何高效地并行实现这些算法的其他版本或优化版本,是值得进一步探究的。本文所做的工作,其运行过程中,数据都是从内存进行读取的,这限制了处理数据的规模。随着信息技术在各种领域的应用,面临着更大规模的数据处理的需要,例如在航天、气象等领域,数据规模和计算量的需求显著高于普通应用。因此,如何合理利用外存,例如SSD、NVM等来进行高效的计算,是一个值得探究的方向。
若想要在一定程度上弥补分布式系统的问题,可以考虑进行相关算法更好的分布式实现,并结合SSD、NVM等存储设备,支持更大规模数据,考虑GPU等加速计算的途径,提高运算性能,以充分发挥已有资源的作用,得到更高效、更经济的系统。
致谢
感谢俞博文和刘家昌在计算机系统结构知识和技术工具的使用方法方面对本文的帮助。利益冲突声明
所有作者声明不存在利益冲突关系。参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
URL [本文引用: 1]
URL [本文引用: 1]
[C]//
[本文引用: 1]
[C]//
[本文引用: 1]
[C]//
[本文引用: 2]
[J].
[本文引用: 1]
URL [本文引用: 1]
[M].
[本文引用: 1]
[J].
[本文引用: 1]
[本文引用: 1]
[C].
[本文引用: 1]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[C].
[本文引用: 1]
[C].
[本文引用: 1]
[C].
[本文引用: 1]
[C].
[本文引用: 1]
[J].
[本文引用: 1]
[C]//
[本文引用: 1]
