Zhuoxuan Xie¹, Ruilin Han^2,31Department of Physics, University of Rochester, NY 14627, United States of America
²Tianjin Xinhua High School, Tianjin 300350, China

First author contact: ³Both authors contributed equally to this work.
Received:2021-08-30Revised:2021-10-18Accepted:2021-10-22Online:2021-11-23


Abstract
Strong electromagnetic fields produced in the non-central heavy-ion collisions can induce vector meson photoproduction. In this paper, we study the photoproduction J/ψ and φ mesons in the relativistic heavy-ion collision from ultra-peripheral nuclear collisions to peripheral hadronic heavy ion collisions. And then include both initial hadronic production and thermal production in quark-gluon plasma (QGP). We find, for the charm anti-charm bound state J/ψ, the photoproduced J/ψs are mainly in the very low momentum region and clearly exceed the hadronic production. However, considering the thermal production of strange quark anti-quark pairs in QGP produced in relativistic heavy-ion collisions, the photoproduced φ is usually smaller than the thermal production and only evident at very peripheral collisions as even their photoproduction is much larger than J/ψ.
Keywords： relativistic heavy ion collisions;photoproduction;quark gluon plasma;charmonium production


PDF (625KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Zhuoxuan Xie, Ruilin Han. Flavor-dependent photoproduction in heavy-ion collisions. Communications in Theoretical Physics, 2021, 73(12): 125301- doi:10.1088/1572-9494/ac3231

1. Introduction

A lattice quantum chromodynamics (QCD) simulation proves the existence of a new phase of matter within high-temperature regions known as quark-gluon plasma (QGP) [1]. And this phase transition can be realized in the experiments by relativistic heavy-ion collisions carried out at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). Recently theoretical studies show that non-central relativistic heavy-ion collisions can generate a strong magnetic field [2, 3]. The maximum of the magnetic field can reach ${eB}\sim 5{m}_{\pi }^{2}$ for semi-central Au+Au collisions at RHIC 200GeV and $\sim 70{m}_{\pi }^{2}$ for semi-central Pb+Pb collisions at LHC energies [3]. The existence of a strong magnetic field in QCD matter induced so many spectacular phenomena, such as magnetic catalysis (MC) and inverse magnetic catalysis (IMC) [4, 5], chiral magnetic effect (CME) [6], enhancement charge particles elliptic flow [7, 8] and so on. In the heavy flavor sector, the strong electromagnetic fields produced in heavy-ion collisions not only affect the heavy quark (quarkonium) production and evolution [9–12] but also induce direct electromagnetic production. Actually, the electromagnetical production has been studied in ultra-peripheral nuclear collisions where the hadronic interaction can be neglected safely [13–16]. However, the magnetic field increase with impact parameters firstly and then decrease until ultra-peripheral nuclear collisions (UPC), which also reaches a maximum at impact parameters ∼12 fm(<2R_A, with R_A is the radius of nucleus.) [3]. In recent experiments it was also indicated that charmonium photoproduction becomes larger than the hadroproduction in the extremely low p_T region even in the semi-central collisions at RHIC [17, 18] and LHC [19].

On the theoretical side, Fermi firstly proposed that the transverse electromagnetic fields can be approximated as a swarm of equivalent photons, called 'Equivalent Photon Approximation' (EPA) [20]. This idea was also extended by Weizsäcker and Williams independently and is therefore also called the 'Weizsäcker-Williams-Method' [21]. This allows a simple and straightforward calculation of photoproduction between the target nucleus and electromagnetic fields [22–24]. Comparing the wavelength of the equivalent photon with the nucleus size, the photoproduction can be divided into coherent and incoherent photoproduction. In the case of coherent photoproduction, the wavelength of the equivalent photon is larger than the nucleus radius and the photon interaction with the whole nucleus [25–30]. If the wavelength of the equivalent photon is short enough to distinguish and then the nucleons or even partons in nucleons, this is known as incoherent photoproduction [31, 32]

Unlike the photoproduction at UPC, one may need to consider both cold nuclear effects [33–36] and hot nuclear effects [37–42] in the peripheral hadronic heavy ion collisions (HHIC). As studied before, the photoproduced produced J/ψ will be partly dissociated in the hot medium and regenerated in the final stage [25]. For strange quarks, their thermal production in hot medium via, for instance, the gluon fusion process ${gg}\to s\bar{s}$, can largely increase their number. It was proposed as a signal of the QGP formation [43]. Due to the strangeness enhancement, the photoproduced φ meson would be not evident comparing with J/ψ.

The paper is organized as follows. After a short introduction to photoproduction, we present the density of the equivalent photon and photoproduction formulas in section 2. In section 3, we discuss both the photoproduction and hadroproduction of J/ψ in UPC and HHIC. And photoproduction and coalescence statistical production φ meson in section 4. Finally. we summarize our study in section 5.

2. Theoretical framework

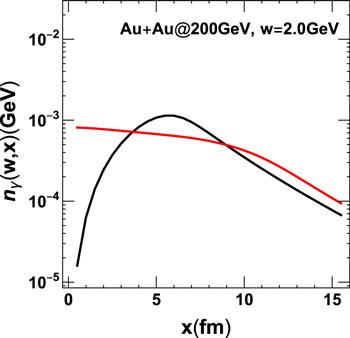
The energy flux of the electromagnetic field through a plane perpendicular to the moving direction of the nucleus is described by the Poynting vector S = E × B. And based on the spirit of the EPA method, the energy flux of the fields through a transverse plane is identical to the energy flux of the equivalent photons, that are also required by energy conservation law. So, the photon flux at a distance r from the central of nucleus is given by [22, 44, 45]:(1)$\begin{eqnarray}\displaystyle \frac{{{\rm{d}}}^{3}{N}_{\gamma }(\omega ,r)}{{\rm{d}}\omega {r}{\rm{d}}{r}{d}\phi }=\displaystyle \frac{{Z}^{2}\alpha }{{\pi }^{2}\omega }{\left|{\int }_{0}^{\infty }{{\rm{d}}{k}}_{T}{k}_{T}^{2}\displaystyle \frac{F({\tilde{k}}_{T}^{2})}{{\tilde{k}}_{T}^{2}}{J}_{1}({{rk}}_{T})\right|}^{2},\end{eqnarray}$where ${\tilde{k}}_{T}^{2}\equiv {k}_{T}^{2}+{\omega }^{2}/{\gamma }^{2}$. α = 1/137 is the EM coupling constant. $\gamma =\sqrt{{s}_{{NN}}}/(2{m}_{p})$ is the Lorentz boost factor in the Lab-frame, which also equals ∼100 at RHIC 200 GeV Au + Au collisions and ∼1000 at LHC Pb + Pb collisions. Z is the proton number in the nucleus. F(q²) is the form factor of the nucleus which is the Fourier transformation of the charge distribution function. And J₁ is the first kind Bessel function. k_T is the transverse momentum of photons.

For the coherent photoproduction, the photon emitted from nucleus A interacts coherently with another nucleus B. We average the photon density over nucleus B. The photon density at certain point r and the averaging value is shown in figure 1.(2)$\begin{eqnarray}\begin{array}{l}{n}_{\gamma }(\omega ,b)={\int }_{0}^{{R}_{A}}\frac{r{\rm{d}}r}{\pi {R}_{A}^{2}}\\ {\int }_{0}^{2\pi }{\rm{d}}\phi \frac{{{\rm{d}}}^{3}{N}_{\gamma }(\omega ,\sqrt{{b}^{2}+2{br}\cos \phi +{r}^{2}})}{{\rm{d}}\omega r{\rm{d}}r{\rm{d}}\phi }.\end{array}\end{eqnarray}$

Figure 1.

New window|Download| PPT slide
Figure 1.The comparison of photon density as a function of distance with/without average over nuclear. The red line represent the average value, while the black is without averaging.


We can see the profile of the photon density before averaged over another nucleus increase firstly, then decreases continually, and reaches a maximum at x ∼ 6fm as the distances get larger and larger. While the photon density monotonically decreases after the average. That means the contribution of photoproduction becomes more and more important from peripheral to central collisions.

The Woods-Saxon distribution for symmetric nuclei:(3)$\begin{eqnarray}\rho (r)=\displaystyle \frac{{\rho }_{0}}{{{\rm{e}}}^{({R}_{A}-r)/a}+1},\end{eqnarray}$where ρ₀ is central density. R_A is the radius of nucleus and a is for edge width of nucleus. r₀ = 6.38 fm and a = 0.535 fm for Au. The nuclear form factor F(q) can be obtained via Fourier transformation of the Woods-Saxon distribution.(4)$\begin{eqnarray}F(q)=\int \rho ({\boldsymbol{r}}){{\rm{e}}}^{{\rm{i}}{\boldsymbol{q}}\cdot {\boldsymbol{r}}}{{\rm{d}}}^{3}{\boldsymbol{r}}.\end{eqnarray}$The electromagnetic fields can not only interact with the other nucleus (γA process) but also with the electromagnetic fields of other nucleus (γγ process). For a charmonium system, the rates for photonuclear (γA) interactions are considerably higher than for comparable two-photon reactions [46, 47]. The photonuclear cross section for vector mesons can be obtained from photon-proton cross section with optical theorem and Glauber calculation,(5)$\begin{eqnarray}{\sigma }_{\gamma A\to {VA}}=\displaystyle \frac{{\rm{d}}{\sigma }_{\gamma A\to {VA}}}{{\rm{d}}{t}}{| }_{t=0}\times {\int }_{-{t}_{\min }}^{\infty }{\rm{d}}{t}| F(t){| }^{2},\end{eqnarray}$where ${t}_{\min }={\left(\displaystyle \frac{{M}_{V}^{2}}{4\omega \gamma }\right)}^{2}$. And,(6)$\begin{eqnarray}\begin{array}{l}\frac{{\rm{d}}{\sigma }_{\gamma A\to {VA}}}{{\rm{d}}t}{| }_{t=0}={C}^{2}\frac{\alpha {\sigma }_{{\rm{tot}}}^{2}({VA})}{4{f}_{v}^{2}},\\ {\sigma }_{{\rm{tot}}}({VA})=2\int {{\rm{d}}}^{2}{{\boldsymbol{x}}}_{T}[1-{{\rm{e}}}^{-\frac{1}{2}{\sigma }_{{\rm{tot}}}({Vp}){T}_{A}({{\bf{x}}}_{T})}],\\ {\sigma }_{{\rm{tot}}}^{2}({Vp})=\frac{4{f}_{v}^{2}}{\alpha {C}^{2}}\frac{d\sigma (\gamma p\to {Vp})}{{\rm{d}}t}{| }_{t=0}.\end{array}\end{eqnarray}$T_A is the nuclear thickness function, f_v is the vector meson photon coupling, C is a correction factor, here we take C = 0.3 for J/ψ [48]. For heavy meson photoproduction, the meson exchange process has been suppressed, and the reaction occurs only though the Pomeron exchange process. The cross section can be parameterized with HERA data as [23]:(7)$\begin{eqnarray}\frac{{\rm{d}}\sigma (\gamma p\to J/\psi p)}{{\rm{d}}t}{| }_{t=0}={b}_{v}({{XW}}^{\epsilon }),\end{eqnarray}$where b_v is the constant and equal 4 GeV⁻² for J/ψ, 7 GeV⁻² for φ. X and ε are the parameters for Pomeron exchange process. We take the same value as the [23]. W is the center-of-mass energy of γ and proton. The coherent photoproduction cross section can be expressed as the product of photon density and photon-nuclear cross section.

With the photon density and the photon-nucleus cross section, we can write the vector meson coherent photoproduction cross section as a function of rapidity in UPC as,(8)$\begin{eqnarray}\frac{{\rm{d}}{\sigma }_{V}}{{\rm{d}}y}(y)=\omega {n}_{\gamma }(\omega ){\sigma }_{\gamma A\to {VA}}(\omega )+(y\to -y),\end{eqnarray}$where ω = e^ym_J/ψ/2 is the photon energy. For the peripheral HHIC, the coherent produced vector mesons as a function of rapidity with impact parameter b can be expressed as,(9)$\begin{eqnarray}\frac{{\rm{d}}{N}_{V}}{{\rm{d}}y}(y| b)=\omega {n}_{\gamma }(\omega ,b){\sigma }_{\gamma A\to {VA}}(\omega )+(y\to -y).\end{eqnarray}$

The transverse momentum distribution of photoproduced vector meson can be expressed as (consider $t={p}_{T}^{2}$):(10)$\begin{eqnarray}\begin{array}{rcl}\frac{{{\rm{d}}}^{2}N}{2\pi {p}_{T}{\rm{d}}{p}_{T}{\rm{d}}y}&=&\frac{1}{\pi {\rm{\Delta }}y}\int \omega {n}_{\gamma }(\omega ,b)\frac{{\rm{d}}{\sigma }_{\gamma A\to J/\psi A}\ \ (\omega ,t)}{{\rm{d}}t}{\rm{d}}y\\ & & +(y\to -y),\end{array}\end{eqnarray}$where:(11)$\begin{eqnarray}\frac{{\rm{d}}{\sigma }_{\gamma A\to J/\psi A}(\omega ,t)}{{\rm{d}}t}=\frac{{\rm{d}}{\sigma }_{\gamma A\to J/\psi A}}{{\rm{d}}t}{| }_{t=0}| F(t){| }^{2}.\end{eqnarray}$

3. J/ψ production

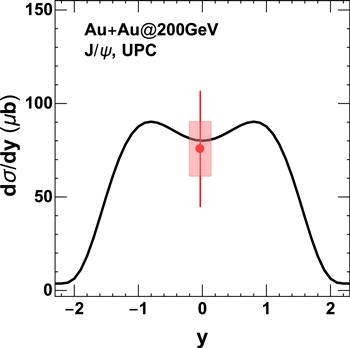
Figure 2 shows the coherent photoproduction cross-section of J/ψ at RHIC in UPC. It can explain the experimental data well. For J/ψ, they are tightly bounded $c\bar{c}$ state, the probability survives in the hot medium produced in heavy-ion collisions. And previous studies show the final yield of J/ψ comes from two parts, initial production and regeneration [42]. For the peripheral hadronic heavy-ion collisions, there is another part, photoproduction. Those three contributions will be accounted and calculated in the following.

Figure 2.

New window|Download| PPT slide
Figure 2.J/ψ coherent photoproduction cross section as a function of rapidity in UPC at 200 GeV Au + Au collisions. The experimental data is from [49].


We firstly concentrate on the initial hadroproduction. The differential cross-section of the J/ψ hadroproduction in p + p collisions has been measured in the experiment [50, 51]. And it can be parameterized as [52, 53]:(12)$\begin{eqnarray}\frac{{{\rm{d}}}^{2}{\sigma }_{J/\psi }^{{pp}}}{2\pi {p}_{T}{\rm{d}}{p}_{T}{\rm{d}}y}=\frac{2(n-1)}{2\pi D(y)}{\left(1+\frac{{p}_{T}^{2}}{D(y)}\right)}^{-n}\frac{{\rm{d}}{\sigma }_{J/\psi }^{{pp}}}{{\rm{d}}y},\end{eqnarray}$where $D(y)=(n-2)\langle {p}_{T}^{2}\rangle (1-{y}^{2}/{Y}^{2})$, the maximum rapidity $Y=\arccos (\sqrt{{s}_{{NN}}}/2{m}_{J/\psi })$. The best fit of the experimental data give n = 6, mean transverse momentum $\langle {p}_{T}^{2}\rangle =4.14\,\mathrm{GeV}$, and ${\rm{d}}{\sigma }_{J/\psi }^{{pp}}/{\rm{d}}y=0.68\mu b$, as shown in figure 3. The yield or momentum spectrum of J/ψ in heavy-ion collisions can be a superposition of p + p collisions.

Figure 3.

New window|Download| PPT slide
Figure 3.The differential cross section of J/ψ in 200 GeV p + p collisions at central rapidity. The line is our parameterization with equation (12).


Now, we come to consider the cold nuclear effect in heavy-ion collisions. For the charmonium production, the cold nuclear matter effect includes usually the nuclear shadowing effect, Cronin effect, and nuclear absorption. At top RHIC energy, the collision time is much shorter than the charmonium formation time and also the formation time of QGP, one can safely neglect the nuclear absorption and just take into account the Cronin effect and shadowing effect [38, 39]. The Cronin effect will broaden the momentum of the initially produced charmonia. The shadowing effect will introduce a modification factor for primordially produced charmonium which is roughly ∼0.8 and dependent on the impact parameter [36].

The hot medium named quark-gluon plasma which is produced in heavy-ion collisions is a very strong coupling system. The evolution can be described by the hydrodynamic equation. For simplicity, we solve the (2+1) D ideal hydrodynamic equations [39] to get the local temperature T(x, τ) and four velocity u^μ(x, τ). One also needs the equation of state of the hot medium. We treat the quark-gluon plasma as an ideal gas of massless gluons, u and d quarks, and strange quark with mass m_s = 150 MeV [54]. Hadron gas is taken to be an ideal gas of all known hadrons and resonances with mass up to 2 GeV. The connection between two phase is constructed with Maxwell law. By changing the initialization for the hydrodynamic equations, we obtain the maximum temperatures T₀ = 320 MeV of the medium at the initial time τ₀ = 0.6 fm/c for 200 GeV Au + Au collisions.

The real-time evolution of J/ψ in hot medium can be described by the Boltzmann equation. And give a good description on J/ψ nuclear modification factor R_AA, anisotropic flows and so on [37–41]. Charmonium dissociation and regeneration rates are proportional to the parton local densities and the charm pair densities in the hot medium, respectively [55, 57, 58]. However, it's difficult to determine the position of J/ψ in a coherent photoproduction process. We aim to consider the modifications of cold and hot matter on photoproduced J/ψ, so we need to know the spatial distributions of them. In this work, we take the spatial distributions f^norm as a function which is proportional to the square of the thickness function ${T}_{A}^{2}({{\boldsymbol{x}}}_{T})$.(13)$\begin{eqnarray}\begin{array}{l}\frac{{\rm{d}}{N}_{V}}{{\rm{d}}y}({\boldsymbol{b}})=\int {{\rm{d}}}^{2}{{\boldsymbol{x}}}_{T}\omega {n}_{\gamma }(\omega ,{\boldsymbol{b}}){\sigma }_{\gamma A\to {VA}}(\omega )\\ \,\times \,{f}^{{\rm{norm}}}({{\boldsymbol{x}}}_{T}+{\boldsymbol{b}}/2)\\ \,\times \,{\left[{{ \mathcal R }}_{g}(x,{\mu }_{F},{{\boldsymbol{x}}}_{T}+{\boldsymbol{b}}/2)\right]}^{2}\times {{\rm{e}}}^{-{\int }_{{\tau }_{0}}^{{\tau }_{f}}{\rm{d}}\tau {\alpha }_{{\rm{\Psi }}}}\\ \,+\,(y\to -y,{\boldsymbol{b}}/2\to -{\boldsymbol{b}}/2),\end{array}\end{eqnarray}$where ${{ \mathcal R }}_{g}$ is the shadowing effect, and the scale can be chosen as ${\mu }_{F}^{2}={M}_{J/\psi }^{2}/4$ GeV² [59]. Causing $t\ll {M}_{J/\psi }^{2}$, the momentum fraction of gluon $x\approx {M}_{J/\psi }^{2}/{W}^{2}={M}_{J/\psi }{e}^{-y}/\sqrt{{s}_{{NN}}}$. The decay rate α_ψ in hot medium which was showed before.

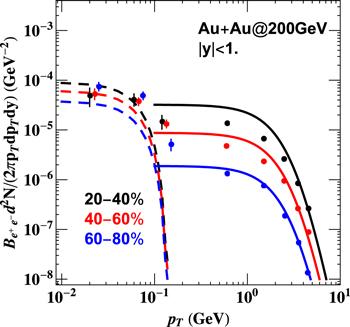
The results which contain those three contributions are shown in figure 4. We can see clearly, the photoproduced J/ψ is mainly in the low p_T(<0.1 GeV) region and largely enhanced compared with hadronic production. This is a clear signal of photoproduction and the existence of strong electromagnetic fields. The photoproduced J/ψ increases with the centrality, which means the electromagnetic fields are increasing with the impact parameters. That is consistent with the results in previous studies [3].

Figure 4.

New window|Download| PPT slide
Figure 4.J/ψ invariant yields for Au + Au collisions as a function of participants p_T at different centralities at mid-rapidity. The dashed lines represent the photoproduction and the solid lines represent the hadroproduction. Both lines are without considering the QGP effect. Where the branching ratio ${B}_{{e}^{+}{e}^{-}}\approx 0.06$. The experimental data is from [56].

4. φ production

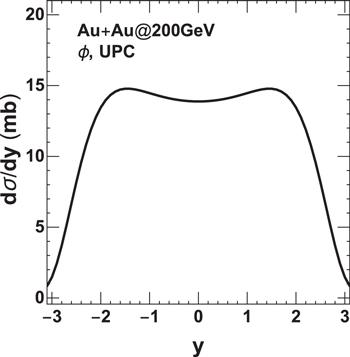
We now turn to studying the yield of vector meson $\phi (s\bar{s})$ in heavy-ion collisions. Based on equation (8), the coherent photoproduction cross-section of φ at RHIC in UPC is calculated, as shown in figure 5. We can see the cross-section is much larger than J/ψ, due to the smaller mass of φ mesons. Different from J/ψ, loosely bound φ is easy to melt in hot medium. And reproduced at the QCD phase boundary, just like light hadrons. So, there are two sources of φ mesons, one is regeneration, another is photoproduction. Their yield can be described well by a statistic-based model, such as the coalescence model. The coalescence mechanism has been successfully used to describe the yield and spectrum of light hadron in the heavy-ion collisions [60–62], especially the quark number scaling of the elliptic flow [63, 64] and the enhancement of the baryon to meson ratio [65]. In this work, we try to use the coalescence model to estimate the yield of φ mesons in heavy-ion collisions.

Figure 5.

New window|Download| PPT slide
Figure 5.φ meson coherent photoproduction cross section as a function of rapidity in UPC at 200 GeV Au + Au collisions.


The formula of coalescence hadronization mechanism can be expressed as,(14)$\begin{eqnarray}\begin{array}{l}\frac{{{\rm{d}}}^{3}N}{{{\rm{d}}}^{2}{{\boldsymbol{P}}}_{T}{\rm{d}}y}=C\int \frac{{{\rm{d}}}^{3}{{\boldsymbol{p}}}_{1}{{\rm{d}}}^{3}{{\boldsymbol{r}}}_{1}}{{\left(2\pi \right)}^{3}{E}_{1}}\frac{{{\rm{d}}}^{3}{{\boldsymbol{p}}}_{2}{{\rm{d}}}^{3}{{\boldsymbol{r}}}_{2}}{{\left(2\pi \right)}^{3}{E}_{2}}{{\boldsymbol{p}}}_{1}\cdot {\rm{d}}{{\boldsymbol{\sigma }}}_{1}{{\boldsymbol{p}}}_{2}\cdot {\rm{d}}{{\boldsymbol{\sigma }}}_{2}\\ \,\times \,{f}_{s}({{\boldsymbol{r}}}_{1},{{\boldsymbol{p}}}_{1}){f}_{\bar{s}}({{\boldsymbol{r}}}_{2},{{\boldsymbol{p}}}_{2})W({\boldsymbol{x}},{\boldsymbol{q}}),\end{array}\end{eqnarray}$where the hadronization hypersurface dΣ_i is determined by hydrodynamic. The constant C = 1/12 is the statistical factor to take into account the inner quantum numbers in forming a colorless hadron. f_i(r_i, p_i) is the distribution function of strange(anti-strange) quark. And it can be treated as thermal distribution ${f}_{i}({x}_{i},{p}_{i})={\gamma }_{s}{N}_{i}/({{\rm{e}}}^{{u}_{\mu }{p}_{i}^{\mu }/T}+1)$ with a fugacity γ_s to consider the non-thermal effect [66]. The degenerate factor N_i = 6. W(x, q) is the coalescence probability with relative coordinate x and momentum q which can be parameterized as a Gaussian distribution and the width it related with the radius of meson [62]. In this study, we take the width Σ = 0.46 fm for φ mesons.

The results are shown in figure 6. We can see the experimental data of φ mesons can be described well with the coalescence model. The photonproduced φ in the peripheral heavy-ion collisions via the Pomeron exchange process is mainly in the low p_T region and smaller than coalescence production in the central and mid-rapidity. This is very different from the J/ψ that the photonproduced is significantly larger than hadroproduction. That's because the strange quark thermal production in QGP, will enhance the yield of φ in heavy-ion collisions. However, strangeness enhancement becomes weak at very peripheral collisions, such as 60%–80% as shown in figure 6. Then, the photoproduction is a little bit larger than coalescence production. That may provide an opportunity to observe the photoproduction effect.

Figure 6.

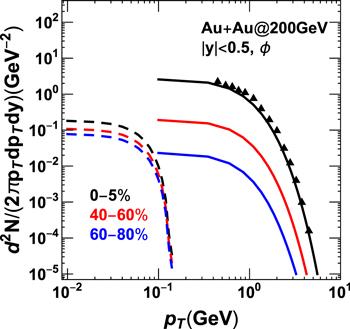New window|Download| PPT slide
Figure 6.The p_T spectrum of φ meson in Au + Au collisions at 200 GeV. The dashed lines represent the photoproduction and the solid lines represent the coalescence production. The experimental data is from [67].

5. Summary

In summary, we study the production of vector meson J/ψ and φ at ultra-peripheral nuclear collisions and peripheral hadronic heavy-ion collisions which include initial production, regeneration, and photoproduction. The results show, the photoproduced J/ψs are mainly in the very low momentum range and clearly exceed the hadronic production even the regeneration supplement. Our results can explain the experimental data. However, due to the strange quark pair thermal production in quark-gluon plasma (QGP) produced in relativistic heavy-ion collisions, the photoproduced φ is usually smaller than the coalescence production and only reveals itself at very peripheral collisions. Based on this study, we can conclude that for heavy quarkonium the photoproduction is significantly dominant at the very low p_T region, while strange or light flavor vector mesons are not obvious as even its photoproduction is much more than that of heavy quarkonium.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Bazavov A et al. 2012 Phys. Rev. D 85 054503
DOI:10.1103/PhysRevD.85.054503 [Cited within: 1]

[2]Skokov V Illarionov A Y Toneev V 2009 Int. J. Mod. Phys. A 24 5925 5932
DOI:10.1142/S0217751X09047570 [Cited within: 1]

[3]Deng W T Huang X G 2012 Phys. Rev. C 85 044907
DOI:10.1103/PhysRevC.85.044907 [Cited within: 4]

[4]Shovkovy I A 2013 Lect. Notes Phys. 871 13
[Cited within: 1]

[5]Bruckmann F Endrodi G Kovacs T G 2013 J. High Energy Phys. JHEP04(2013)112
DOI:10.1007/JHEP04(2013)112 [Cited within: 1]

[6]Fukushima K Kharzeev D E Warringa H J 2008 Phys. Rev. D 78 074033
DOI:10.1103/PhysRevD.78.074033 [Cited within: 1]

[7]Tuchin K 2012 J. Phys. G 39 025010
DOI:10.1088/0954-3899/39/2/025010 [Cited within: 1]

[8]Basar G Kharzeev D Skokov V 2012 Phys. Rev. Lett. 109 202303
DOI:10.1103/PhysRevLett.109.202303 [Cited within: 1]

[9]Alford J Strickland M 2013 Phys. Rev. D 88 105017
DOI:10.1103/PhysRevD.88.105017 [Cited within: 1]

[10]Das S K Plumari S Chatterjee S Alam J Scardina F Greco V 2017 Phys. Lett. B 768 260
DOI:10.1016/j.physletb.2017.02.046

[11]Zhao J Zhou K Chen S Zhuang P 2020 Prog. Part. Nucl. Phys. 114 103801
DOI:10.1016/j.ppnp.2020.103801

[12]Brandenburg J D Zha W Xu Z arXiv:2103.16623 [hep-ph]
[Cited within: 1]

[13]Bertulani C A Baur G 1988 Phys. Rept. 163 299
DOI:10.1016/0370-1573(88)90142-1 [Cited within: 1]

[14]Bertulani C A Klein S R Nystrand J 2005 Ann. Rev. Nucl. Part. Sci. 55 271
DOI:10.1146/annurev.nucl.55.090704.151526

[15]Adam J et al. (ALICE Collaboration) 2015 Phys. Lett. B 751 358
DOI:10.1016/j.physletb.2015.10.040

[16]Abelev B B et al. (ALICE Collaboration) 2014 Phys. Rev. Lett. 113 232504
DOI:10.1103/PhysRevLett.113.232504 [Cited within: 1]

[17]Krueger K et al. (STAR Collaboration) 2019 Phys. Rev. Lett. 123 132302
DOI:10.1103/PhysRevLett.123.132302 [Cited within: 1]

[18]Zha W (STAR) 2017 Nucl. Part. Phys. Proc. 289–290 414 416
DOI:10.1016/j.nuclphysbps.2017.05.096 [Cited within: 1]

[19]Adam J et al. (ALICE Collaboration) 2016 Phys. Rev. Lett. 116 222301
DOI:10.1103/PhysRevLett.116.222301 [Cited within: 1]

[20]Fermi E 1924 Z. Phys. 29 315
DOI:10.1007/BF03184853 [Cited within: 1]

[21]von Weizsacker C F 1934 Z. Phys. 88 612
DOI:10.1007/BF01333110 [Cited within: 1]

[22]Krauss F Greiner M Soff G 1997 Prog. Part. Nucl. Phys. 39 503
DOI:10.1016/S0146-6410(97)00049-5 [Cited within: 2]

[23]Klein S Nystrand J 1999 Phys. Rev. C 60 014903
DOI:10.1103/PhysRevC.60.014903 [Cited within: 2]

[24]Zha W Brandenburg J D Tang Z Xu Z 2020 Phys. Lett. B 800 135089
DOI:10.1016/j.physletb.2019.135089 [Cited within: 1]

[25]Shi W Zha W Chen B 2018 Phys. Lett. B 777 399
DOI:10.1016/j.physletb.2017.12.055 [Cited within: 2]

[26]Chen B Greiner C Shi W Zha W Zhuang P arXiv:1801.01677 [hep-ph]


[27]Yu G Cai Y Fu Y Yang H Gao Q Hu Q Hu L Li W Song Y arXiv:2105.06880 [hep-ph]


[28]Lappi T Mantysaari H 2013 Phys. Rev. C 87 032201
DOI:10.1103/PhysRevC.87.032201

[29]Zha W Ruan L Tang Z Xu Z Yang S 2019 Phys. Lett. B 789 238 242
DOI:10.1016/j.physletb.2018.12.041

[30]Zha W Ruan L Tang Z Xu Z Yang S 2019 Phys. Rev. C 99 061901
DOI:10.1103/PhysRevC.99.061901 [Cited within: 1]

[31]Yu G M Cai Y B Li Y D Wang J S 2017 Phys. Rev. C 95 014905
DOI:10.1103/PhysRevC.95.014905 [Cited within: 1]

[32]Yang Y Cai S Cai Y Xiang W 2019 Nucl. Phys. A 990 17 28
DOI:10.1016/j.nuclphysa.2019.06.012 [Cited within: 1]

[33]Mueller A H Qiu J w 1986 Nucl. Phys. B 268 427
DOI:10.1016/0550-3213(86)90164-1 [Cited within: 1]

[34]Cronin J W Frisch H J Shochet M J Boymond J P Mermod R Piroue P A Sumner R L 1975 Phys. Rev. D 11 3105
DOI:10.1103/PhysRevD.11.3105

[35]Gerschel C Hufner J 1988 Phys. Lett. B 207 253
DOI:10.1016/0370-2693(88)90570-9

[36]Eskola K J Paukkunen H Salgado C A 2011 Nucl. Phys. A 855 150 157
DOI:10.1016/j.nuclphysa.2011.02.032 [Cited within: 2]

[37]Zhao X Rapp R 2011 Nucl. Phys. A 859 114
DOI:10.1016/j.nuclphysa.2011.05.001 [Cited within: 2]

[38]Zhou K Xu N Xu Z Zhuang P 2014 Phys. Rev. C 89 054911
DOI:10.1103/PhysRevC.89.054911 [Cited within: 1]

[39]Chen B Guo T Liu Y Zhuang P 2017 Phys. Lett. B 765 323 327
DOI:10.1016/j.physletb.2016.12.021 [Cited within: 2]

[40]Chen B Liu Y Zhou K Zhuang P 2013 Phys. Lett. B 726 725 728
DOI:10.1016/j.physletb.2013.09.036

[41]Chen B Hu M Zhang H Zhao J 2020 Phys. Lett. B 802 135271
DOI:10.1016/j.physletb.2020.135271 [Cited within: 1]

[42]Zhao J Chen B 2018 Phys. Lett. B 776 17 21
DOI:10.1016/j.physletb.2017.11.014 [Cited within: 2]

[43]Rafelski J Muller B 1982 Phys. Rev. Lett. 48 1066
DOI:10.1103/PhysRevLett.48.1066 [Cited within: 1]

Rafelski J Muller B 1986 Phys. Rev. Lett. 56 2334Erratum:
DOI:10.1103/PhysRevLett.48.1066 [Cited within: 1]

[44]Zha W Brandenburg J D Ruan L Tang Z Xu Z 2021 Phys. Rev. D 103 033007
DOI:10.1103/PhysRevD.103.033007 [Cited within: 1]

[45]Zha W Tang Z arXiv:2103.04605 [hep-ph]
[Cited within: 1]

[46]Ginzburg I F Panfil S L Serbo V G 1988 Nucl. Phys. B 296 569
DOI:10.1016/0550-3213(88)90033-8 [Cited within: 1]

[47]Baranov S Cisek A Klusek-Gawenda M Schafer W Szczurek A 2013 Eur. Phys. J. C 73 2335
DOI:10.1140/epjc/s10052-013-2335-8 [Cited within: 1]

[48]Zha W et al. 2018 Phys. Rev. C 97 044910
DOI:10.1103/PhysRevC.97.044910 [Cited within: 1]

[49]Conesa del Valle Z (PHENIX Collaboration)Contribution to: XLIV Rencontres de Moriond on QCD and High Energy Interactions 287 290
[Cited within: 1]

[50]Adare A et al. (PHENIX Collaboration) 2007 Phys. Rev. Lett. 98 232002
DOI:10.1103/PhysRevLett.98.232002 [Cited within: 1]

[51]Zha W Huang B Ma R Ruan L Tang Z Xu Z Yang C Yang Q Yang S 2016 Phys. Rev. C 93 024919
DOI:10.1103/PhysRevC.93.024919 [Cited within: 1]

[52]Liu Y Qu Z Xu N Zhuang P 2010 J. Phys. G 37 075110
DOI:10.1088/0954-3899/37/7/075110 [Cited within: 1]

[53]Chen B 2019 Chin. Phys. C 43 124101
DOI:10.1088/1674-1137/43/12/124101 [Cited within: 1]

[54]Sollfrank J Huovinen P Kataja M Ruuskanen P V Prakash M Venugopalan R 1997 Phys. Rev. C 55 392
DOI:10.1103/PhysRevC.55.392 [Cited within: 1]

[55]Liu Y Chen B Xu N Zhuang P 2011 Phys. Lett. B 697 32 36
DOI:10.1016/j.physletb.2011.01.026 [Cited within: 1]

[56]Zha W (STAR) 2017 J. Phys. Conf. Ser. 779 012039
DOI:10.1088/1742-6596/779/1/012039 [Cited within: 1]

[57]Chen B Zhuang P Xu Z Xu N 2016 Phys. Rev. C 93 054905
DOI:10.1103/PhysRevC.93.054905 [Cited within: 1]

[58]Chen B 2017 Phys. Rev. C 95 034908
DOI:10.1103/PhysRevC.95.034908 [Cited within: 1]

[59]Guzey V Kryshen E Zhalov M 2016 Phys. Rev. C 93 055206
DOI:10.1103/PhysRevC.93.055206 [Cited within: 1]

[60]Fries R J Muller B Nonaka C Bass S A 2003 Phys. Rev. C 68 044902
DOI:10.1103/PhysRevC.68.044902 [Cited within: 1]

[61]Greco V Ko C M Levai P 2003 Phys. Rev. C 68 034904
DOI:10.1103/PhysRevC.68.034904

[62]Plumari S Minissale V Das S K Coci G Greco V 2018 Eur. Phys. J. C 78 348
DOI:10.1140/epjc/s10052-018-5828-7 [Cited within: 2]

[63]Molnar D Voloshin S A 2003 Phys. Rev. Lett. 91 092301
DOI:10.1103/PhysRevLett.91.092301 [Cited within: 1]

[64]Lin Z W Ko C M 2002 Phys. Rev. Lett. 89 202302
DOI:10.1103/PhysRevLett.89.202302 [Cited within: 1]

[65]Hwa R C Yang C B 2003 Phys. Rev. C 67 034902
DOI:10.1103/PhysRevC.67.034902 [Cited within: 1]

[66]Castorina P Plumari S Satz H 2017 Int. J. Mod. Phys. E 26 1750081
DOI:10.1142/S0218301317500811 [Cited within: 1]

[67]Adler S S et al. (PHENIX Collaboration) 2005 Phys. Rev. C 72 014903
DOI:10.1103/PhysRevC.72.014903 [Cited within: 1]