Gong-Ming Yu^,1,2,?, Yan-Bing Cai^,3,?, Zhen Bai^,1,§, Qiang Hu^,11 CAS Key Laboratory of High Precision Nuclear Spectroscopy and Center for Nuclear Matter Science, Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou 730000, China
2 Institute for Nuclear Theory, University of Washington, Box 351550, Seattle, WA 98195, USA
3 Guizhou Key Laboratory in Physics and Related Areas, Guizhou University of Finance and Economics, Guiyang 550025, China

Corresponding authors: ^?E-mail:ygmanan@impcas.ac.cn^?E-mail:myparticle@163.com^§E-mail:baizh@impcas.ac.cnE-mail:qianghu@impcas.ac.cn

Received:2018-12-7Online:2019-05-1

Fund supported:

National Natural Science Foundation of China under Grant.11847207 International Postdoctoral Exchange Fellowship Program of China under Grant.20180010 China Postdoctoral Science Foundation funded project.2017M610663

Abstract
We calculate the centrality dependence of inclusive cross section of large-$p_{T}$ charmed-meson ($D^{0}$, $D^{*}$, $D^{*+}$, and $D_{s}^{+}$) from heavy quark fragmentation by the hard photoproduction processes in ultrarelativistic heavy ion collisions. The numerical results indicate that the contribution of the hard photoproduction processes cannot be negligible for the inclusive charmed-meson production in Au-Au collisions at Relativistic Heavy Ion Collider (RHIC) and Pb-Pb collisions at Large Hadron Collider (LHC).
Keywords： Charmed-meson;Photoproduction processes;Relativistic heavy ion collision


PDF (1990KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Gong-Ming Yu, Yan-Bing Cai, Zhen Bai, Qiang Hu. Centrality Dependence of Charmed-Meson Photoproduction in Ultrarelativistic Heavy Ion Collisions. [J], 2019, 71(5): 563-567 doi:10.1088/0253-6102/71/5/563

1 Introduction

Recent measurements of charmed-meson ($D^{0}$, $D^{*}$, $D^{*+}$, and $D_{s}^{+}$) production in high energy hadronic collisional experiment reported by PHENIX Collaboration^[1] and STAR collaboration^[2-8] at Relativistic Heavy Ion Collider (RHIC), as well as ALICE Collaboration,^[9-17] ATLAS Collaboration,^[18] and LHCb Collaboration^[19-20] at Large Hadron Collider (LHC) have shown that inclusive heavy-quark production provides us with an important tool for the test of the predictions of perturbative quantum chromodynamics (pQCD),^[21-22] and the evolution of charm quark in hot partonic medium can be considered as the probe of the quark-gluon plasma (QGP) produced in ultrarelativistic heavy ion collisions.^[23-38] Indeed, many phenomenological models such as the color glass condensate (CGC) effective theory,^[39] general-mass variable-favor-number scheme,^[40-42] $k_{T}$-factorization approach,^[43-44] fragmentation approach,^[45-47] Parton-Hadron-String Dynamics (PHSD) transport approach,^[48] heavy quark recombination mechanism,^[49-50] two-component HYDJET++ model,^[51-52] gluon splitting with Langevin transport model,^[53] POWLANG transport model,^[54] double-parton scattering (DPS) mechanisms,^[55] quark coalescence model,^[56] and single- and central-diffractive mechanisms in the Ingelman-Schlein model^[57] have been proposed for the calculation of charmed-meson production.

In this paper, we extend the hard photoproduction mechanism^[58-64] in the quasi-real photon approximation, that plays an important role in the electron-proton deep inelastic scattering at the Hadron Electron Ring Accelerator (HERA), to the heavy quark fragmentation production of charmed-meson in Au-Au collisions at RHIC and Pb-Pb collisions at LHC. The photoproduction mechanism may be direct that the high-energy photons from the charged parton interact with the parton from the nucleus, as well as resolved that the hadron-like photons interact with the parton.

The paper is organized as follows. In Sec. 2 we present the hard photoproduction processes for charmed-meson at RHIC and LHC energies. The conclusion is given in Sec. 3.

2 General Formalism

The centrality dependence of differential cross section for inclusive charmed-meson hadroproduction from leading order (LO) can be expressed as

(1)$\frac{dN^{\rm LO}}{dp_{T}^{2}dy}=\int d^{2}bdx_{a}dx_{b}T_{A}(\pmb{\it r})T_{B}(|\pmb{\it r}-\pmb{\it b}|) f_{a/A}(x_{a},Q^{2},\pmb{\it r}) \\ \times f_{b/B}(x_{b},Q^{2},|\pmb{\it r}-\pmb{\it b}|)\frac{x_{a}x_{b}}{x_{a}x_{b}-\tau}\frac{d\hat{\sigma}}{d\hat{t}}(ab \rightarrow cd) \\ \times \frac{D_{H/c}(z_{c})}{z_{c}},$
where the variables $x_{a}$ and $x_{b}=(x_{a}x_{2}-\tau)/(x_{a}-x_{1})$ are momentum fractions of the partons, $z_{c}=p_{H}/p_{c}$ is the momentum fraction of the final charmed-meson, $x_{1}=({1}/{2})(x_{T}^{2}+4\tau)^{1/2}\exp(y)$, $x_{2}=({1}/{2})(x_{T}^{2}+4\tau)^{1/2}\exp(-y)$, $x_{T}=2p_{T}/\sqrt{s}$, $\tau=(M/\sqrt{s})^{2}$, and $M$ is the mass of the charmed-meson; $({d\hat{\sigma}}/{d\hat{t}})(ab\rightarrow cd)$ is the differential cross section for the subprocess^[65-66] such as $q\bar{q}\rightarrow Q\bar{Q}$, $qQ\rightarrow qQ$, $gQ\rightarrow gQ$, and $gg\rightarrow Q\bar{Q}$; $D_{H/c}(z_{c})$ is the Peterson heavy quark fragmentation function into charmed-meson,^[67] as well as $T_{A}(\pmb{\it r})$ is the nuclear thickness function^[68-69] normalized to $\int d^{2}r T_{A}(\pmb{\it r})=A$. We choose the transverse momentum scale as $Q^{2}=p_{T}^{2}$.

The parton distribution function (PDF) is given by^[70]

(2)$ f_{a/A}(x,Q^{2},\pmb{\it r})=R_{a/A}(x,Q^{2},\pmb{\it r}) \Bigl[\frac{Z}{A}f_{a/p}(x,Q^{2}) \\ +\Bigl(1-\frac{Z}{A}\Bigr)f_{a/n}(x,Q^{2})\Bigr],$
where $Z$ is the charge and $A$ the mass number of the nucleus. The PDF parametrization^[71] will be used for nucleon parton distributions $f_{a/N}(x,Q^{2})$. The parton shadowing factor $R_{a/A}(x,Q^{2},\pmb{\it r})$ describes the nuclear modification of parton distributions per nucleon inside the nucleus and can be given by the parametrization.^[72-75]

In the inelastic direct photoproduction processes (inel.dir.), the centrality dependence of differential cross section of inclusive large-$p_{T}$ charmed-meson production in the hadronic collisions can be expressed as

(3)$ \frac{dN^{\rm inel.dir.}}{dp_{T}^{2}dy} = \int d^{2}bd^{2}rdx_{a} dx_{b}dz_{a}T_{A}(\pmb{\it r})T_{B}(|\pmb{\it r}-\pmb{\it b}|) \\ \times f_{a/A}(x_{a},Q^{2}, \pmb{\it r}) f_{\gamma/q}(z_{a}) f_{b/B}(x_{b},Q^{2},|\pmb{\it r}-\pmb{\it b}|) \\ \times\frac{x_{a}x_{b}z_{a}}{x_{a}x_{b}z_{a}-\tau} \frac{d\hat{\sigma}}{d\hat{t}}(\gamma b\rightarrow cd)\frac{D_{H/c}(z_{c})}{z_{c}}, $
here $({d\hat{\sigma}}/{d\hat{t}})(\gamma b\rightarrow cd)$ is the differential cross section for the subprocess,^[76] and the equivalent photon spectrum function for the charged parton is given by Refs. ^[77-78]

(4)$f_{\gamma/q}(x)=\frac{\alpha}{2\pi}e_{f}^{2}\Bigl\{\frac{1+(1-x)^{2}}{x}\Bigl[\ln\Bigl(\frac{E}{m}\Bigr)-\frac{1}{2}\Bigr] +\frac{x}{2}\Bigl[\ln\Bigl(\frac{2}{x}-2\Bigr) \\ +1\Bigr]+\frac{(2-x)^{2}}{2x}\ln\Bigl(\frac{2-2x}{2-x}\Bigr)\Bigr\},$
where $e_{f}$, $E$, and $m$ are the charge, energy, and mass of the parton, respectively.

In the inelastic resolved photoproduction processes (inel. res.), the centrality dependence of differential cross section for inclusive large-$p_{T}$ charmed-meson production in the hadronic collisions can be written as

(5)$ \frac{dN^{\rm inel.res.}}{dp_{T}^{2}dy} = \int d^{2}bd^{2}rdx_{a} dx_{b}dz_{a}dz'_{a}T_{A}(\pmb{\it r})T_{B}(|\pmb{\it r}-\pmb{\it b}|) \\ \times f_{a/A}(x_{a},Q^{2},\pmb{\it r})f_{\gamma/q}(z_{a}) f_{\gamma}(z'_{a},Q^{2}) \\ \times f_{b/B}(x_{b},Q^{2},|\pmb{\it r}-\pmb{\it b}|)\frac{x_{a}x_{b}z_{a}z'_{a}}{x_{a}x_{b}z_{a}z'_{a}-\tau} \\ \times \frac{d\hat{\sigma}}{d\hat{t}} (a'b\rightarrow cd)\frac{D_{H/c}(z_{c})}{z_{c}},$
where $f_{\gamma}(z'_{a},Q^{2})$ is PDF for the hadron-like photon.^[79]

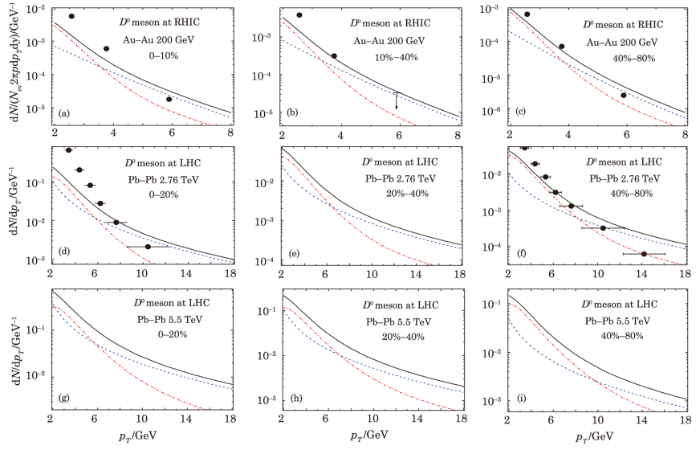
The numerical results of our calculation for large-$p_{T}$ charmed-meson from the hard photoproduction processes are plotted in Figs. 1-4. Compared with the leading order (the dashed line) and the charmed-meson data of STAR Collaboration^[3] and ALICE Collaboration,^[9,12] we find that the large-$p_{T}$ charmed-meson produced by the hard photoproduction processes (the dashed-dotted line) cannot be negligible, that is because of the equivalent photon spectrum for the charged parton, $f_{\gamma/q}\propto\ln(E/m_{q})=\ln(\sqrt{s}/2m_{q})+\ln(x)$, becomes prominent since the collision energy $\sqrt{s}$ is very large at RHIC and LHC energies.

Fig. 1

New window|Download| PPT slide
Fig. 1(Color online) The centrality dependence of inclusive cross section of large transverse momentum $D^{0}$ meson production in the nucleus-nucleus collisions at RHIC and LHC energies. The dashed line (blue line) for the initial parton hard scattering processes (LO), the dashed-dotted line (red line) for the inelastic photoproduction processes, and the solid line (black) is for the sum of the above processes. The $D^{0}$ meson data points are from the STAR Collaboration^[3] and ALICE Collaboration.^[9]

Fig. 2

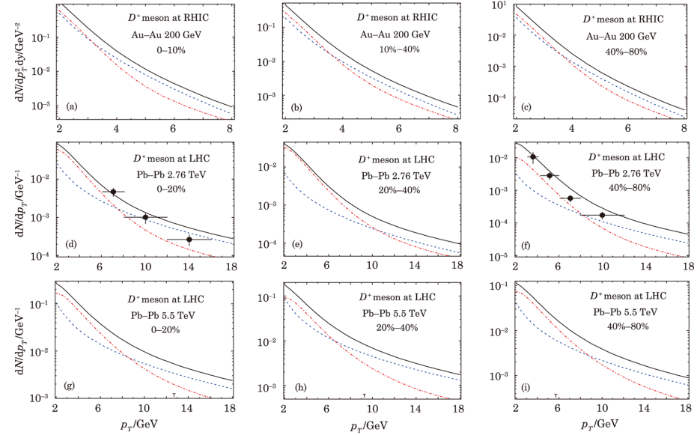
New window|Download| PPT slide
Fig. 2(Color online) The centrality dependence of inclusive cross section of large transverse momentum $D^{*}$ meson production in the nucleus-nucleus collisions at RHIC and LHC energies. The dashed line (blue line) for the initial parton hard scattering processes (LO), the dashed-dotted line (red line) for the inelastic photoproduction processes, and the solid line (black) is for the sum of the above processes. The $D^{*}$ meson data points are from ALICE Collaboration.^[9]

Fig. 3

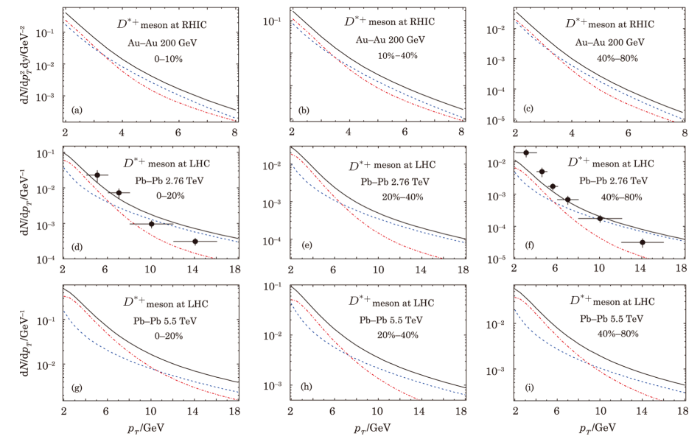
New window|Download| PPT slide
Fig. 3(Color online) The centrality dependence of inclusive cross section of large transverse momentum $D^{*+}$ meson production in the nucleus-nucleus collisions at RHIC and LHC energies. The dashed line (blue line) for the initial parton hard scattering processes (LO), the dashed-dotted line (red line) for the inelastic photoproduction processes, and the solid line (black) is for the sum of the above processes. The $D^{*+}$ meson data points are from ALICE Collaboration.^[9]

Fig. 4

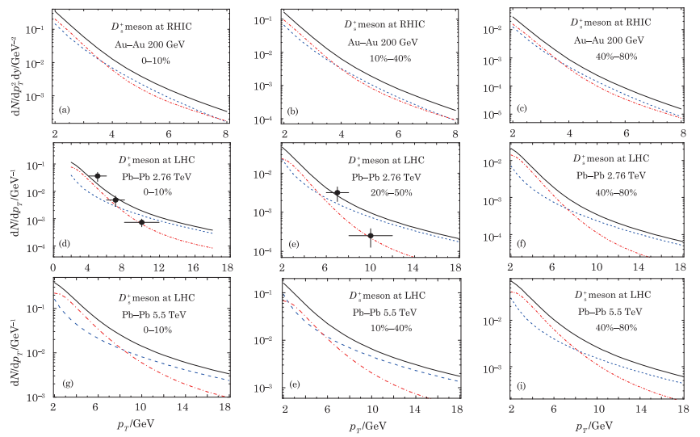
New window|Download| PPT slide
Fig. 4(Color online) The centrality dependence of inclusive cross section of large transverse momentum $D_{s}^{+}$ meson production in the nucleus-nucleus collisions at RHIC and LHC energies. The dashed line (blue line) for the initial parton hard scattering processes (LO), the dashed-dotted line (red line) for the inelastic photoproduction processes, and the solid line (black) is for the sum of the above processes. The $D_{s}^{+}$ meson data points are from ALICE Collaboration.^[12]

3 Conclusion

We have investigated the heavy quark fragmentation production of large-$p_{T}$ charmed-meson from the direct and resolved hard photoproduction processes in Au-Au collisions at Relativistic Heavy Ion Collider (RHIC) and Pb-Pb collisions at Large Hadron Collider (LHC). At the early stage of relativistic heavy ion collisions, the charged parton of the incident nucleus can emit high photons (hadron-like photons) that can interact with the partons of the nucleus by the photon-gluon fusion (the quark-antiquark annihilation, quark-gluon Compton scattering, and gluon-gluon fusion interactions). The numerical results indicate that the contribution of charmed-meson produced by the hard photoproduction processes cannot be negligible, that is because of the very large photon spectrum in the quasi-real approximation, in the nucleus-nucleus collisions at RHIC and LHC energies.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] J. Matthew Durham, et al., (PHENIX Collaboration), Nucl. Phys. A 932 (2014)81.
[Cited within: 1]

[2] L. Adamczyk, et al., (STAR collaboration), Phys. Rev. D 86 (2012)072013
[Cited within: 1]

[3] L. Adamczyk, et al., (STAR Collaboration), Phys. Rev. Lett. 113 (2014)142301.
[Cited within: 2]

[4] M. R. Lomnitz, et al., (STAR collaboration), Nucl. Phys. A 956 (2016)256.


[5] M. Mustafa, et al., (STAR Collaboration), Nucl. Phys. A 956 (2016)43.


[6] Md. Nasim, et al., (STAR collaboration), Nucl. Phys. A 956 (2016)509.


[7] G. N. Xie, et al., (STAR Collaboration), Nucl. Phys. A 956 (2016)473.


[8] L. Adamczyk, et al., (STAR collaboration), Phys. Rev. Lett. 118 (2017)212301.
[Cited within: 1]

[9] B. Abelev, et al., (ALICE Collaboration), J. High Energy Phys. 09 (2012)112.
[Cited within: 5]

[10] B. Abelev, et al., (ALICE Collaboration), Phys. Lett. B 718 (2012)279.


[11] B. Abelev, et al., (ALICE Collaboration), Phys. Rev. Lett. 111 (2013)102301


[12] J. Adam, et al., (ALICE Collaboration), J. High Energy Phys. 03 (2016)082.
[Cited within: 2]

[13] B. Abelev, et al., (ALICE Collaboration), Phys. Rev. Lett. 113 (2014)232301.


[14] J. Adam, et al., (ALICE Collaboration), J. High Energy Phys. 09 (2015)148.


[15] J. Adam, et al., (ALICE Collaboration), J. High Energy Phys. 11 (2015)205


[16] F. Colamaria, et al., (ALICE Collaboration), Nucl. Phys. A 956 (2016)497.


[17] J. Adam, et al., (ALICE Collaboration), Eur. Phys. J. C 77 (2017)245.
[Cited within: 1]

[18] G. Aad, et al., (ATLAS Collaboration), Nucl. Phys. B 907 (2016)717.
[Cited within: 1]

[19] R. Aaij, et al., (LHCb Collaboration), Phys. Lett. B 718 (2013)902.
[Cited within: 1]

[20] R. Aaij , et al., (LHCb Collaboration), Nucl. Phys. B 871 (2013)1.
[Cited within: 1]

[21] J. C. Collins, D. E. Soper, and G. F. Sterman, Nucl. Phys. B 263 (1986)37.
[Cited within: 1]

[22] R. D. Field , Applications of Perturbative QCD, Addison-Wesley Publishing Company, Reading, MA(1989).
[Cited within: 1]

[23] R. Averbeck , Prog. Part. Nucl. Phys. 70 (2013)159.
[Cited within: 1]

[24] T. Buchheim, T. Hilger, and B. Kampfer, EPJ Web Conf. 81 (2014)05007.


[25] M. Djordjevic and M. Djordjevic, Phys. Rev. C 90 (2014)034910.


[26] M. He, R. J. Fries, and R. Rapp, Phys. Rev. C 91 (2015)024904.


[27] M. Nahrgang, J. Aichelin, S. Bass, et al., Phys. Rev. C 91 (2015)014904.


[28] S. S. Cao, G. Y. Qin, and S. A. Bass, Phys. Rev. C 92 (2015)024907.


[29] S. S. Cao, G. Y. Qin, and S. A. Bass, Phys. Rev. C 92 (2015)054909.


[30] K. Saraswat, P. Shukla, and V. Singh, Nucl. Phys. A 943 (2015)83.


[31] A. Beraudo, A. De Pace, M. Monteno , et al., J. Phys.: Conf. Ser. 612 (2015)012035.


[32] A. Andronic , et al., Eur. Phys. J. C 76 (2016)107.


[33] F. Prino and R. Rapp , J. Phys. G: Nucl. Part. Phys. 43 (2016)093002.


[34] B. Chen, K. Zhou, and P. Zhuang, Phys. Rev. C 86 (2012)03490.


[35] B. Chen, Y. Liu, K. Zhou, and P. Zhuang, Phys. Lett. B 726 (2013)725.


[36] B. Chen, T. Guo, Y. Liu, and P. Zhuang, Phys. Lett. B 765 (2017)323.


[37] J. Zhao and B. Chen, Phys. Lett. B 776 (2018)17.


[38] B. Chen and J. Zhao, Phys. Lett. B 772 (2017)819.
[Cited within: 1]

[39] H. Fujii and K. Watanabe, Nucl. Phys. A 920 (2013)78.
[Cited within: 1]

[40] B. A. Kniehl, G. Kramer, I. Schienbein, and H. Spiesberger, Phys. Rev. D 79 (2009)094009.
[Cited within: 1]

[41] B. A. Kniehl, G. Kramer, I. Schienbein, and H. Spiesberger , Eur. Phys. J. C 62 (2009)365.


[42] B. A. Kniehl, G. Kramer, I. Schienbein, and H. Spiesberger , Eur. Phys. J. C 2 (2012)2082.
[Cited within: 1]

[43] R. Maciula and A. Szczurek, Phys. Rev. D 87 (2013)094022.
[Cited within: 1]

[44] R. Maciula, A. Szczurek, and M. Luszczak, Phys. Rev. D 92 (2015)054006.
[Cited within: 1]

[45] B. A. Kniehl, G. Kramer, I. Schienbein, and H. Spiesberger, Phys. Rev. D 71 (2005)014018.
[Cited within: 1]

[46] B. A. Kniehl and G. Kramer, Phys. Rev. D 74 (2006)037502.


[47] L. S. Kisslinger, M. X. Liu, and P. McGaughey , Int. J. Theor. Phys. 55 (2016)2026.
[Cited within: 1]

[48] T. Song, H. Berrehrah, D. Cabrera, et al., Phys. Rev. C 93 (2016)034906.
[Cited within: 1]

[49] W. K. Lai, A. K. Leibovich, and A. A. Petrov, Phys. Rev. D 90 (2014)054022.
[Cited within: 1]

[50] A. K. Leibovich and W. K. Lai, Phys. Rev. D 91 (2015)054022.
[Cited within: 1]

[51] I. P. Lokhtin, A. V. Belyaev, G. Kh. Eyyubova , et al., J. Phys.: Conf. Ser. 668 (2016)012068.
[Cited within: 1]

[52] I. P. Lokhtin, A. V. Belyaev, G. Kh. Eyyubova , et al., J. Phys. G: Nucl. Part. Phys. 43 (2016)125104.
[Cited within: 1]

[53] S. S. Cao, G. Y. Qin, and X. N. Wang, Phys. Rev. C 93 (2016)024912.
[Cited within: 1]

[54] A. Beraudo, A. De. Pace, and H. Monteno, et al., Nucl. Phys. A 956 (2016)501.
[Cited within: 1]

[55] R. Maciula, V. A. Saleev, A. V. Shipilova, A. Szczurek, Phys. Lett. B 758 (2016)458.
[Cited within: 1]

[56] R. Esha, Md. Nasim, H. Z. Huang , J. Phys. G: Nucl. Part. Phys. 44 (2017)045109.
[Cited within: 1]

[57] M. Luszczak, R. Maciula, and A. Szczurek, Phys. Rev. D 91 (2015)054024.
[Cited within: 1]

[58] J. R. Forshaw, AIP Conf. Proc. 407 (1997)73.
[Cited within: 1]

[59] R. Nisius, Phys. Rep. 332 (2000)165.


[60] M. Krawczyk, A. Zembrzuski, and M. Staszel, Phys. Rep. 345 (2001)265.


[61] G. M. Yu and Y. D. Li, Phys. Rev. C 91 (2015)044908.


[62] G. M. Yu, Y. B. Cai, Y. D. Li, and J. S. Wang, Phys. Rev. C 95 (2017)014905.


[63] G. M. Yu, Y. C. Yu, Y. D. Li, and J. S. Wang, Nucl. Phys. B 917 (2017)234.


[64] W. Shi, W. M. Zha, and B. Y. Chen, Phys. Lett. B 777 (2018)399.
[Cited within: 1]

[65] B. L. Combridge, Nucl. Phys. B 151 (1979)429.
[Cited within: 1]

[66] T. C. Yuan, Phys. Rev. D 50 (1994)5664.
[Cited within: 1]

[67] C. Peterson, D. Schlatter, I. Schmitt, and P. M. Zerwas, Phys. Rev. D 27 (1983)105.
[Cited within: 1]

[68] C. Y. Wong, Phys. Rev. D 30 (1984)961.
[Cited within: 1]

[69] Y. C. Wong , Introduction to High Energy Heavy-Ion Collisions, World Scientific, Singapore (1994).
[Cited within: 1]

[70] X. F. Chen, T. Hirano, E. K. Wangk, et al., Phys. Rev. C 84 (2011)034902.
[Cited within: 1]

[71] M. Glück, E. Reya, and A. Vogt, Z. Phys. C 53 (1992)127.
[Cited within: 1]

[72] X. N. Wang and M. Gyulassy, Phys. Rev. D 44 (1991)3501.
[Cited within: 1]

[73] X. N. Wang and M. Gyulassy, Phys. Rev. Lett. 68 (1992)1480.


[74] W. T. Deng, X. N. Wang, and R. Xu, Phys. Rev. C 83 (2011)014915.


[75] K. Abdel-Waged and N. Felemban, Phys. Rev. C 91 (2015)034908.
[Cited within: 1]

[76] J. Babcock, D. Sivers, and S. Wolfram, Phys. Rev. D 18 (1978)162.
[Cited within: 1]

[77] S. J. Brodsky, T. Kinoshita, and H. Terazawa, Phys. Rev. D 4 (1971)1532.
[Cited within: 1]

[78] B. A. Kniehl, Phys. Lett. B 254 (1991)267.
[Cited within: 1]

[79] M. Glück, E. Reya, and I. Schienbein , Phys. Rev. D 60 (1999)054019.
[Cited within: 1]