Ying-Di Huang, Jia-Ting Xie, Su-Mei Hu, Yan He^,Guangdong University of Petrochemical Technology, Maoming 525000, China

Received:2020-08-06Revised:2020-11-03Accepted:2020-11-05Online:2021-01-07


Abstract
In order to clarify the edge and interface effect on the adhesion energy between graphene (Gr) and its substrate, a theoretical model is proposed to study the interaction and strain distribution of Gr/Si system in terms of continuum medium mechanics and nanothermodynamics. We find that the interface separation and adhesion energy are determined by the thickness of Gr and substrate. The disturbed interaction and redistributed strain in the Gr/Si system induced by the effect of surface and interface can make the interface adhesion energy decrease with increasing thickness of Gr and diminishing thickness of Si. Moreover, our results show that the smaller area of Gr is more likely to adhere to the substrate since the edge effect improves the active energy and strain energy. Our predictions can be expected to be a guide for designing high performance of Gr-based electronic devices.
Keywords： graphene;edge effect and interface confinement;strain distribution;adhesion energy


PDF (936KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Ying-Di Huang, Jia-Ting Xie, Su-Mei Hu, Yan He. Edge effect and interface confinement modulated strain distribution and interface adhesion energy in graphene/Si system. Communications in Theoretical Physics, 2021, 73(1): 015702- doi:10.1088/1572-9494/abc7ad

1. Introduction

Graphene (Gr) has attracted much attention in the past decade as it provides a real possibility for a high performance of batteries, nanoelectronic and optoelectronic devices, photovoltaic, energy storage, etc [1–4]. Supported on a substrate, the tunable interaction between Gr and its substrate play a significant role on the interface adhesion energy of Gr/substrate system [5–7]. Although much strategies both from experimentally [8–11] and theoretically [12–14] have been made to study the adhesion properties by controlling the thickness, size and substrate morphology, the interactions and contacts between Gr and substrate remain one of the significant challenges in the fundamental scientific owing to the influence of interface, edge and surface effects [15].

Generally, the interface adhesion energy of Gr/substrate relates to its thickness and edge condition as well as the surface state of substrate. On the one hand, reducing the thickness of Gr can not only enhance the surface-to-volume ratio (SVR), but also make the strain redistribution in Gr/substrate system [16, 17]. On the other hand, the interface interactions between Gr and substrate are very sensitive to the surface of substrate. The surface state of substrate can modulate the long-range interaction of van der Waals interaction and short-range interactions of interface bonds as well as out of plane rippling behaviors, resulting in the change of interface adhesion energy [18–20]. Moreover, the interface effect induced by the discrepancy of lattice constant between film and substrate has an important influence on interface interaction as well. For example, Huang et al [21, 22] reported that the stress in the interface of film/substrate can induce the films wrinkles and the tunable interface adhesion and interface strain between films and substrate can be achieved by controlling the thickness of films or the sample of substrate. Even more than that, the interface effect can also disturb the orientation of π- and σ-orbital and simultaneously induce the in-plane and out-of-plane strain to be taken place, resulting in the change the mechanical properties of Gr such as Young’s modulus and Poisson’s ratio [23, 24]. Especially, as the unsaturated dangling bonds in the edge carbon atoms, the strong bonds would be formed in Gr/substrate system and the mechanical properties of the Gr depend on the edge chirality [25, 26]. In this case, when decreasing the area or size of Gr, the strain would be redistributed in the Gr/substrate systems due to the enhancement of SVR, resulting in the change of the interaction and adhesion energy in various edge chirality of Gr.

In order to clarify the influence of edge effect and interface confinement on interface adhesion properties of Gr/substrate system, rectangular Gr and circular Gr is investigated in terms of continuum medium mechanics and nanothermodynamics. Our results show that surface, interface and edge effect can disturb the total energy of Gr/substrate system, resulting in change of interface separation and adhesion energy. The tunable strain transfer in Gr/substrate system is also studied by modulating size and thickness of Gr and substrate.

2. Principle

In order to evaluate the edge, surface and interface effect on the adhesion properties, a type Gr/Si system is deliberately considered in our model. We assume that a Gr membrane with area ${A}_{g}$ and thickness ${t}_{f}$ is covered on the surface of Si substrate, as shown in the inset of figure 1(a). Theoretically, the total free energy ${U}_{{\rm{total}}}$ of the Gr/substrate system can be expressed as(1)$\begin{eqnarray}{U}_{{\rm{total}}}=-{U}_{{\rm{vdW}}}-{U}_{{\rm{vdW}}}^{{\rm{extra}}}+\displaystyle \displaystyle \sum _{\phi =f,s}{U}_{s}^{\phi },\end{eqnarray}$where ${U}_{{\rm{total}}}$ is the van der Waals interaction between Gr and substrate, and ${U}_{{\rm{vdW}}}^{{\rm{extra}}}$ denotes extra energy induced by the interaction between the edge of the carbon atoms and the substrate of the Si atoms [27], ${U}_{s}^{f}$ and ${U}_{s}^{s},$ are, respectively, strain energy of Gr and substrate.

Figure 1.

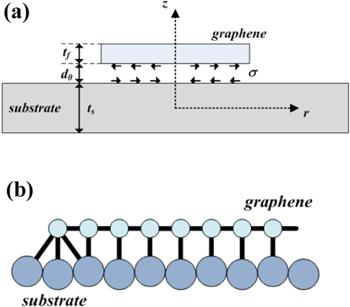New window|Download| PPT slide
Figure 1.(a) Schematic illustration of a Gr membrane on substrate, (b) Gr interacting with its substrate.


In general, the van der Waals (vdWs) interaction between a carbon atom and the substrate atom can be expressed by Lennard-Jones potential: ${W}_{{\rm{LJ}}}=-{C}_{1}/{d}^{6}+{C}_{2}/{d}^{12},$ where $d$ is the distance between two atoms, ${C}_{1}$ and ${C}_{2}$ are the constants for the attractive and repulsive interaction. It is noteworthy that the vdWs interaction of Gr/substrate system is predominantly stored on the first layer of Gr and substrate which contributes almost 99% of the total energy [12]. Therefore, the total interaction potential between substrate and Gr membrane can be obtained by integrating all the atoms of first layer of Gr and substrate: ${W}_{p}=\displaystyle {\int }_{{A}_{g}}\displaystyle {\int }_{{V}_{0}}{W}_{{\rm{LJ}}}{\rho }_{s}{\rho }_{g}{\rm{d}}{V}_{s}{\rm{d}}{A}_{g},$ where ${\rho }_{s}$ and ${\rho }_{g}$ are the number of atoms per unit area of a monolayer graphene and the number of atoms per unit volume of the substrate, and ${V}_{s}$ is the substrate volume. Consequently, the interfacial potential energy can be expressed as(2)$\begin{eqnarray}{U}_{{\rm{vdW}}}=-{{\rm{\Gamma }}}_{0}\left[\displaystyle \frac{3}{2}{\left(\displaystyle \frac{{d}_{0}}{d}\right)}^{3}-\displaystyle \frac{1}{2}{\left(\displaystyle \frac{{d}_{0}}{d}\right)}^{9}\right],\end{eqnarray}$${d}_{0}$ and ${{\rm{\Gamma }}}_{0}$ are the interface separation under the equilibrium state and the intrinsic adhesion energy per unit area in the bulk case.

In addition, as the abrupt termination of the bonding network in the edge of Gr, a high density of defects and dangling bonds would be left in the boundary [25, 27]. Therefore, the extra bonds of C–Si will be produced, as shown in figure 1(b). Generally, the energy, ${U}_{{\rm{vdW}}}^{{\rm{extra}}},$ induced by the extra energy of C–Si in the edge of Gr, as shown in figure 1. Lahiri et al [27] and Kozlov et al [28] reported that Pauli repulsion equilibrates vdW attraction with donation/back-donation being negligible when the distance of Gr-substrate close to 0.3 nm and the energy is still dominated by the vdW contribution. Thus, the energy, ${U}_{{\rm{vdW}}}^{{\rm{extra}}},$ can be approximately given by the vdWs interaction of C–Si as the distance of Gr–Si is about 0.3 nm [8, 29], i.e.(3)$\begin{eqnarray}{U}_{{\rm{vdW}}}^{{\rm{extra}}}={z}_{s}{\gamma }_{f}{U}_{{\rm{vdW}}},\end{eqnarray}$where ${z}_{s}$ and ${\gamma }_{f}={h}_{0}\tau $ are, respectively, the CNs of edge carbon atom and the ratio of edge atoms to total atoms of the Gr membrane, $\tau $ is the shape factor of rectangular Gr nanoribbons ($\tau =2/W$ for zigzag and armchair) and circular Gr sheet with diameter D ($\tau =4/D$), $W$ and ${h}_{0}$ are, respectively, the width of graphene nanoribbons and the bond length of the bulk case.

Moreover, consider a Gr membrane attached on the surface of Si substrate, the mismatch strain would be taken place as the discrepancy of lattice constant between Gr and substrate. The strain of radial and tangential are ${\varepsilon }_{{\rm{rr}}}={\rm{d}}u/{\rm{d}}r$ and ${\varepsilon }_{\theta \theta }=u/r,$ where $u$ and $r$ are the radial displacements and radial coordinate. Moreover, according to the linear elastic constitutive model and the equilibrium of forces requires, $\tfrac{{\rm{d}}{N}_{{\rm{r}}}^{\phi }}{{\rm{d}}r}+\tfrac{{N}_{r}^{\phi }-{N}_{\theta }^{\phi }}{r}\pm \sigma =0,$ with ${N}_{r}^{\phi }\left(\phi =f,s\right)=\tfrac{{E}_{2{\rm{D}}}^{\phi }}{1-{v}_{\phi }^{2}}\left(\tfrac{{\rm{d}}{u}_{\phi }}{{\rm{d}}r}+{v}_{\phi }\tfrac{{u}_{\phi }}{r}-\left(1+{v}_{\phi }\right){\varepsilon }_{m}\right)$ and ${N}_{\theta }^{\phi }\left(\phi =f,s\right)=\tfrac{{E}_{2{\rm{D}}}^{\phi }}{1-{v}_{\phi }^{2}}\left({v}_{\phi }\tfrac{{\rm{d}}{u}_{\phi }}{{\rm{d}}r}+\tfrac{{u}_{\phi }}{r}-\left(1+{v}_{\phi }\right){\varepsilon }_{m}\right),$ where ${E}_{2{\rm{D}}}^{\phi }={Y}_{\phi }{t}_{\phi }$ is the in-plane stiffness of the 2D material, $+\sigma $ and $-\sigma $ are for the thin film and substrate within the film portion, respectively, and the $\sigma $ vanishes for the substrate outside the film. ${Y}_{f}$ (${Y}_{s}$), ${t}_{f}$ (${t}_{s}$) and ${v}_{f}$ (${v}_{s}$) denote the Young’s modulus, thickness and Poisson’s ratio, $\sigma =\tfrac{{Y}_{s}{t}_{s}\kappa }{6{t}_{f}\left(1-v\right)}$ is the shear stress, $\kappa $ is the curvature of the system, ${\varepsilon }_{m}$ presents the axisymmetric misfit strain distribution [30, 31]. Therefore, we have(4a)$\begin{eqnarray}\displaystyle \frac{{{\rm{d}}}^{2}{u}_{f}}{{\rm{d}}{r}^{2}}+\displaystyle \frac{1}{r}\displaystyle \frac{{\rm{d}}{u}_{f}}{{\rm{d}}r}-\displaystyle \frac{{u}_{f}}{{r}^{2}}=\displaystyle \frac{1-{v}_{f}^{2}}{{E}_{2{\rm{D}}}^{f}}\sigma +\left(1+v\right)\displaystyle \frac{{\rm{d}}{\varepsilon }_{m}}{{\rm{d}}r},\end{eqnarray}$(4b)$\begin{eqnarray}\displaystyle \frac{{{\rm{d}}}^{2}{u}_{s}}{{\rm{d}}{r}^{2}}+\displaystyle \frac{1}{r}\displaystyle \frac{{\rm{d}}{u}_{s}}{{\rm{d}}r}-\displaystyle \frac{{u}_{s}}{{r}^{2}}=-\displaystyle \frac{1-{v}_{s}^{2}}{{E}_{2{\rm{D}}}^{s}}\sigma .\end{eqnarray}$

Additionally, the approach of atomistic-bond-relaxation suggests that the nanostructures can be considered as a shell-core configuration [6, 13, 32]. The internal atoms in core remain have the intrinsic properties, whereas the bond length of the external atoms in shell would shrink spontaneously and the bond energy at equilibrium atomic separation will rise in absolute energy as reduction of the atomic coordination number (CN). Therefore, the strain induced by the surface effect can be deduced as, ${\varepsilon }_{{\rm{surf}}}=\displaystyle \sum _{i\lt {n}_{s}}{\varepsilon }_{i}{h}_{i}/{t}_{f}.$ Moreover, consider the high coordination imperfection of atoms located at the edges of nanostructure, the average strain induced by the edge effect can be given by, ${\varepsilon }_{{\rm{edge}}}=\displaystyle \sum _{{\rm{edge}}}{\gamma }_{{\rm{edge}}}{\varepsilon }_{{\rm{edge}}}{h}_{{\rm{edge}}}/{t}_{f},$ ${\gamma }_{{\rm{edge}}}={\gamma }_{f}$ for Gr and ${\gamma }_{{\rm{edge}}}={\gamma }_{s}$ for substrate [32]. Therefore, considering the discrepancy state of the surface, edge and core atoms, the total strain of the Gr and Si substrate can be obtained(5)$\begin{eqnarray}\begin{array}{l}{\varepsilon }_{\phi }\left(\phi =f,s\right)\\ \,=\,\displaystyle \frac{{\sum }_{i\lt {n}_{s}}{\varepsilon }_{i}^{\phi }{h}_{i}^{\phi }+{\gamma }_{\phi }{\varepsilon }_{{\rm{edge}}}^{\phi }{h}_{{\rm{edge}}}^{\phi }+{\sum }_{jj=rr,\theta \theta }\left({t}_{\phi }-{\sum }_{i\lt {n}_{s}}{h}_{i}^{\phi }\right)}{{t}_{\phi }},\end{array}\end{eqnarray}$${h}_{i}$ (${h}_{{\rm{edge}}}$) and ${\varepsilon }_{i}$ (${\varepsilon }_{{\rm{edge}}}$) are, respectively, the bond length and lattice strain of in surface and edge atoms, and the lattice strain satisfy $\varepsilon ={c}_{i}-1,$ ${c}_{i}=2/\left(1+\exp \left(\left({z}_{b}-{z}_{i}\right)/8{z}_{i}\right)\right)$ is the bond contraction coefficient, the ratio of edge atoms to total atoms of the substrate is zero, ${z}_{i}$ and ${z}_{b}$ are effective CNs in the ith atomic layer and that of bulk case, respectively. Therefore, according to the continuum mechanics principle, the strain energy per unit area stored in graphene membranes can be given by(6)$\begin{eqnarray}{U}_{s}^{\phi }\left(\phi =f,s\right)=\displaystyle {\int }_{{A}_{g}}\displaystyle {\int }_{{t}_{\phi }}\displaystyle \frac{{Y}_{\phi }{\varepsilon }_{\phi }^{2}}{2\left(1-{v}_{\phi }^{2}\right)}{\rm{d}}h{\rm{d}}{A}_{g},\end{eqnarray}$where ${Y}_{\phi }=\tfrac{{z}_{b}^{\phi }}{{z}_{\phi }}\left[\displaystyle {\sum }_{i\lt {n}_{s}}{\gamma }_{\phi }^{\phi }\left({z}_{{\rm{ib}}}^{\phi }{c}_{{\rm{i}}\phi }^{-m}-1\right)\right]{\left(1+{\varepsilon }_{\phi }\right)}^{-3}{Y}_{\phi }^{B}$ is the thickness-dependence Young’s modulus [13], ${z}_{{\rm{ib}}}={z}_{i}/{z}_{b}.$ $\left\langle z\right\rangle ={\gamma }_{\phi }\left({z}_{i}-{z}_{b}\right),$ and $m$ is the bond nature indicator, $m=2.56$ for carbon and $m=4.88$ for silicon [33].

3. Results and discussion

In order to clarify the relationship between adhesion properties and edge effect in Gr/Si substrate system, we consider that the edge carbon atoms that have unsaturated dangling bonds form strong bonds with the Si atoms [27] and the substrate is flat and infinite in the in-plane direction so that the ripple, edge buckling, and steps effect are ignored. Note that the necessary parameters are listed in table 1 and the interface adhesion energy can be calculated by ${\rm{\Gamma }}=-{U}_{{\rm{total}}}$ [12].


Table 1.
Table 1.Input parameters for calculations. r₀, a, h₀, E, v and Y_B are the interface equilibrium distance, in-plane lattice constant, bond length, binding energy per unit area, Poisson’s ratio and Young’s modulus, respectively.

	r0 (nm)	a (nm)	d0 (nm)	E (meV Å−2)	$\nu $	YB (GPa)
Graphene	0.34 [13]	0.245 [12]	0.142 [12]	17.01 [13]	0.16 [8]	1000 [13]
Si		0.54 [43]	0.235 [43]		0.218 [43]	169.2 [43]

New window|CSV

Figure 2 shows the transfer of total strain from Gr to Si substrate with change the thickness of Gr and substrate. The tensile strain in graphene membranes and the compressive strain in substrate are, respectively, increasing and decaying as the thickness of substrate increases or films thickness decreases, whereas the width of graphene exhibit a slight effect on the total strain of Gr and substrate unless the width (radius) of rectangular (circular) Gr less than 1 nm. This result can be attributed to the change of elastic properties as well as surface and edge effect, which leads to the bonds become stronger and reestablish a new self-equilibrium state in Gr/substrate system. As a result, the strain will be redistributed in Gr and substrate. Geandier and co-workers [34] measured that strain transfer from a polymer substrate to the adherent thin films can be obtained by using synchrotron XRD techniqueat a low strain regime. Moreover, He et al [35, 36] and Schadler et al [37, 38] also reported that the strain in thin films are plotted as a function of the applied strains to the substrate, suggest elastic stress and strain transfer behaviors can be achieved in films/substrate system. Noted that we consider the stress and strain are uniformly distributed in Gr membrane and substrate. Those results may deviate from the experimental measurements and simulations which shows the different strains in various positions and layers of Gr [18, 21, 39]. In our case, the uniformly distribution strain in Gr and substrate is suitability for calculating the interfacial adhesion energy, ${\rm{\Gamma }},$ due to the total free energy of the nanosystem is not change.

Figure 2.

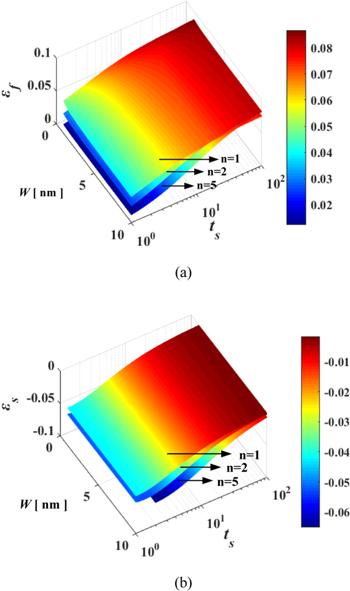New window|Download| PPT slide
Figure 2.The total strain as a function of width of Gr and thickness of Si in (a) Gr and (b) Si.


In order to study the elastic strain and its energy affect on the interface properties. Figure 3 demonstrates interface the equilibrium state in two types of Gr/substrate systems, including rectangular Gr/Si and circular Gr/Si. Clearly, the equilibrium state and the minimum of total energy of those two types of systems have obvious shift with the thickness of Gr. Meanwhile, the thickness dependence of a relative change of interface separation is shown in the inset of figures 3(a) and (b). The variation of interface separation of those two systems decays monotonically with decreasing number of Gr layers, whereas it has slightly increases when reduction the size of Gr. This result is expected since the elastic strain and strain energy increases dramatically with decreasing thickness and size. Moreover, according to the theory of Sun [33] and Ouyang et al [32], the changed physical properties in nanostructures can be attributed to the generation of strain and strain energy as the position of atoms deviate from the intrinsic state. Those results suggest that the elastic properties are insensitive to the size of Gr membrane. Zhao et al [40] and Han et al [26] reported that the size effect on Young’s modulus and Poisson’s ratio can be negligible when the diagonal length and width of Gr nanoribbon beyond 10 nm and 2 nm, respectively.

Figure 3.

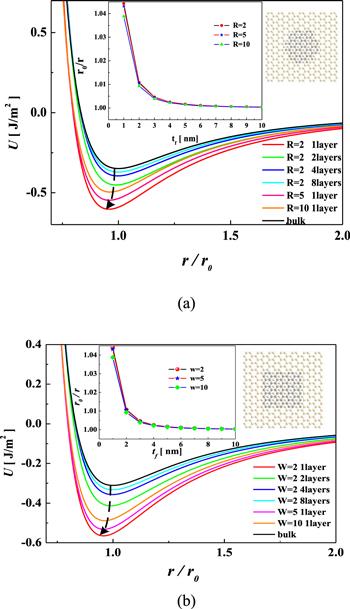New window|Download| PPT slide
Figure 3.The total free energy as a function of number of layers and interfacial separation of Gr in (a) rectangular Gr with R=2, 5, 10 nm and (b) circular Gr with W=2, 5, 10 nm. The inset of (a) and (b) show the relationship between the critical interface separation and the membrane thickness under various R and W, respectively.


Furthermore, in order to explore the influence of edge effect and interface confinement on the adhesion properties. Thickness- and size-dependent interface adhesion energy are shown in figure 4. Evidently, the adhesion energy increases with decaying thickness and size of Gr membrane at first, and then it become a constant when thickness and the size of Gr lager than 5 layers and 2 nm, respectively. Our predictions are consistent with Koenig’s [8] and Gao’s [29] measurements, and these results can be attributed to the difference of elastic properties and strain energy in graphene membranes [13, 41]. Moreover, to clarify the significant of edge on interface adhesion properties, figure 4(b) shows the interface adhesion energy of zigzag edge Gr compared with that of armchair edge Gr, and we have ${{\rm{\Gamma }}}^{{\rm{zig}}}\gt {{\rm{\Gamma }}}^{{\rm{arm}}}$ at fixed layer and width of Gr. This result can be ascribed to the difference edge state and mechanical properties between those two systems. Moreover, compared with figure 4(a), the adhesion energy of rectangular Gr is less than that of radius Gr. This result can be explained to the lower edge state and strain energy as well as the difference self-equilibrium state.

Figure 4.

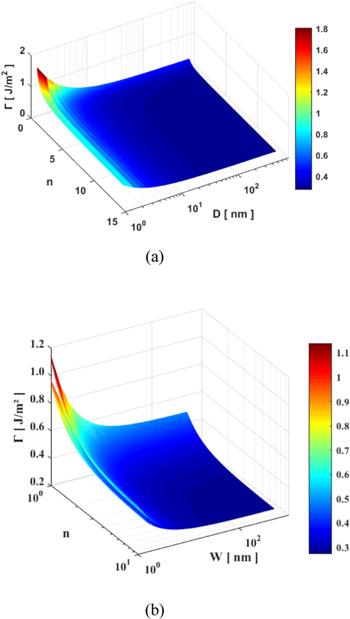New window|Download| PPT slide
Figure 4.Interface adhesion energy as a function of number of layers and size in (a) circular Gr membranes, and (b) Gr zigzag and armchair Gr nanoribbons.


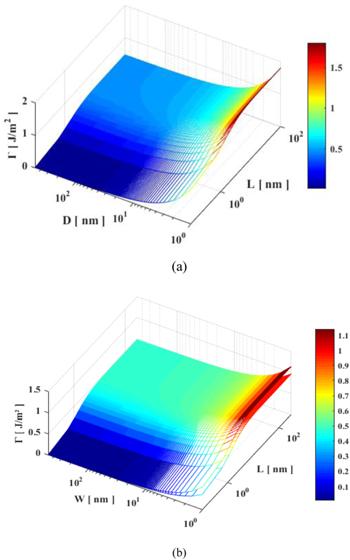
Figure 5 shows the relationship between interface adhesion energy and thickness of substrate or area of single layer Gr. As plotted in figure 5(a), the interface adhesion energy decreases with diminishing thickness of substrate, whereas its increases with decreasing size of Gr. This result suggests that the Gr membranes are more likely to adhere to the thicker substrate. This trend is attributed to the change of vdW interaction, ${U}_{{\rm{vdW}}}^{{\rm{extra}}}$ and strain energy. In fact, decrease the thickness of substrate and area of Gr can not only decay the interaction potential between Gr and substrate, but also make the strain redistributed in the system. Figure 5(b) exhibits the interface adhesion energy of zigzag edge Gr compared with that of armchair edge Gr at various thickness of substrate and area of single layer Gr. The results are similar to figure 4(b) with ${{\rm{\Gamma }}}^{{\rm{zig}}}\gt {{\rm{\Gamma }}}^{{\rm{arm}}}$ at fixed layer and size of Gr, and the increase trend of adhesion energy of rectangular Gr is slightly less than that of circular Gr. Moreover, according to the calculation, the adhesion energy between single layer Gr and silicene is ∼0.3 J m⁻², which is lower than that of Koening’s [8] and Gao’s [29] results, 0.45 J m⁻², suggest the total energy of Gr/substrate can be disturbed by edge and interface confinement. For instance, the parameters of Lennard-Jones potential are $\varepsilon =7.236\,{\rm{meV}}$ and $\sigma =0.3258\,{\rm{nm}}$ in our calculation, which are lower than Rappe’s results with $\varepsilon =8.908\,{\rm{meV}}$ and $\sigma =0.3326\,{\rm{nm}}$ [42]. The discrepancy between our results and Rappe’s result suggests that: (i) the ripple effect of Gr play an important role on the interfacial adhesion energy of Gr/Si; (ii) the interfacial adhesion energy of Gr/SiO₂ (or Gr/Si) may larger than Koenig’s [8] and Gao’s [29] results, 0.45 J m⁻².

Figure 5.

New window|Download| PPT slide
Figure 5.Interface adhesional energy as a function of size and thickness of Si in (a) circular Gr, and (b) Gr zigzag and armchair Gr nanoribbons.

4. Conclusion

In summary, interface adhesion of rectangular Gr/Si substrate and circular Gr/Si substrate nanosystems are studied based on continuum medium mechanics and nanothermodynamics. Our results demonstrate that the surface, interface and edge effect determine the equilibrium state and interface separation distance of Gr/Si substrate nanosystem, which have a significant influence on its strain distribution. As a result, strain transfer between Gr and substrate can be modulated by controlling width and thickness of Gr and substrate. Moreover, we find the adhesion energy decreases with decreasing width and thickness of Gr and substrate, suggesting that the thinner Gr membrane is more likely to adhere on a thicker substrate.

Acknowledgments

This work was supported by the Natural Science Foundation of Guangdong Province (Grant Nos. 2019A1515010916 and 2018A030307028), the Featured Innovation Project of Guangdong Education Department (2018KTSCX150), the Maoming Natural Science Foundation of Guangdong, China, (Grant No. 2019018001) and the Guangdong Province Major Foundation of Fundamental Research (Grant No. 517042).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]El-Kady M F Shao Y L Kaner R B 2016 Nat. Rev. Mater. 1 16033
DOI:10.1038/natrevmats.2016.33 [Cited within: 1]

[2]Kinloch I A Suhr J Jun L Young R J Ajayan P M 2018 Science 362 547
DOI:10.1126/science.aat7439

[3]Li C L Cao Q Wang F Xiao Y Q Li Y B Delaunay J J Zhu H W 2018 Chem. Soc. Rev. 47 4981
DOI:10.1039/C8CS00067K

[4]Rosli N N Ibrahim M A Ludin N A Teridi M A M Sopian K A 2019 Renew. Sustain. Energy Rev. 99 83
DOI:10.1016/j.rser.2018.09.011 [Cited within: 1]

[5]Peak E Hwang G S 2013 J. Appl. Phys. 113 164901
DOI:10.1063/1.4801880 [Cited within: 1]

[6]He Y Yu W B Ouyang G 2014 Phys. Chem. Chem. Phys. 16 11390
DOI:10.1039/C4CP00633J [Cited within: 1]

[7]Anagnostopoulos G Sygellou L Paterakis G Polyzos I Aggelopoulos C A Galiotis C 2019 Nanotechnology 30 015704
DOI:10.1088/1361-6528/aae683 [Cited within: 1]

[8]Koenig S P Boddeti N G Dunn M L Bunch J S 2011 Nat. Nanotechnol. 6 543
DOI:10.1038/nnano.2011.123 [Cited within: 6]

[9]Miskin M Sun C Cohen I Dichtel W R McEuen P 2018 Nano Lett. 18 449
DOI:10.1021/acs.nanolett.7b04370

[10]Tripathi M Awaja F Bizão R A Signetti S Iacob E Paolicelli G Valeri S Dalton A B Pugno N M 2018 ACS Appl. Mater. Interfaces 10 44614
DOI:10.1021/acsami.8b10294

[11]Fan N Guo J Jing G Y Liu C Wang Q Wu G Y Jiang H Peng B A 2020 Nanoscale Adv. 2 2548
DOI:10.1039/C9NA00660E [Cited within: 1]

[12]Aitken Z H Huang R 2010 J. Appl. Phys. 107 123531
DOI:10.1063/1.3437642 [Cited within: 5]

[13]He Y Chen W F Yu W B Ouyang G Yang G W 2013 Sci. Rep. 3 2660
DOI:10.1038/srep02660 [Cited within: 6]

[14]Chen Z Vazirisereshk M R Khajeh A Martini A 2019 J. Phys. Chem. Lett. 10 6455
DOI:10.1021/acs.jpclett.9b02501 [Cited within: 1]

[15]Dai Z H Lu N S Liechti K M Huang R 2020 Curr. Opin. Solid State Mater. Sci. 24 100837
DOI:10.1016/j.cossms.2020.100837 [Cited within: 1]

[16]Kim S Ryu S 2016 Carbon 100 283
DOI:10.1016/j.carbon.2016.01.001 [Cited within: 1]

[17]Dai Z H Liu L Q Zhang Z 2019 Adv. Mater. 31 1805417
DOI:10.1002/adma.201805417 [Cited within: 1]

[18]Na S R Suk J W Ruoff R S Huang R Liechti K M 2014 ACS Nano 8 11234
DOI:10.1021/nn503624f [Cited within: 2]

[19]Kumar S Parks D Kamrin K 2016 ACS Nano 10 6552
DOI:10.1021/acsnano.6b00382

[20]Ghanbari Shohany B Roknabadi M R Kompany A 2016 Commun. Theor. Phys. 65 99
DOI:10.1088/0253-6102/65/1/99 [Cited within: 1]

[21]Huang R Suo Z 2002 J. Appl. Phys. 91 1135
DOI:10.1063/1.1427407 [Cited within: 2]

[22]Jiang T Huang R Zhu Y 2014 Adv. Funct. Mater. 24 396
DOI:10.1002/adfm.201301999 [Cited within: 1]

[23]Wang G R Dai Z H Wang Y L Tan P H Liu L Q Xu Z P Wei Y G Huang R Zhang Z 2017 Phys. Rev. Lett. 119 036101
DOI:10.1103/PhysRevLett.119.036101 [Cited within: 1]

[24]Wang G R Dai Z H Xiao J K Feng S Z Weng C X Liu L Q Xu Z P Huang R Zhang Z 2019 Phys. Rev. Lett. 123 116101
DOI:10.1103/PhysRevLett.123.116101 [Cited within: 1]

[25]Lu Q Gao W Huang R 2011 Modelling Simul. Mater. Sci. Eng. 19 054006
DOI:10.1088/0965-0393/19/5/054006 [Cited within: 2]

[26]Han G R Sun J S Jiang J W 2018 J. Appl. Phys. 123 064301
DOI:10.1063/1.5012562 [Cited within: 2]

[27]Lahiri J Miller T S Ross A J Adamska L Oleynik I I Batzill M 2011 New J. Phys. 13 025001
DOI:10.1088/1367-2630/13/2/025001 [Cited within: 4]

[28]Kozlov S M Viñes F Görling A 2012 J. Phys. Chem. C 116 7360
DOI:10.1021/jp210667f [Cited within: 1]

[29]Gao X Y Yu X Y Li B X Fan S C Li C 2017 Adv. Mater. Interfaces 4 1601023
DOI:10.1002/admi.201601023 [Cited within: 4]

[30]Freund L B 2000 J. Mech. Phys. Solids 48 1159
DOI:10.1016/S0022-5096(99)00070-8 [Cited within: 1]

[31]Feng X Huang Y Jiang H Ngo D Rosakis A J 2006 J. Mech. Mater. Struct. 1 1041
DOI:10.2140/jomms.2006.1.1041 [Cited within: 1]

[32]Zhu Z M Zhang A Ouyang G Yang G W 2011 Appl. Phys. Lett. 98 263112
DOI:10.1063/1.3605683 [Cited within: 3]

[33]Sun C Q 2009 Prog. Mater. Sci. 54 179
DOI:10.1016/j.pmatsci.2008.08.001 [Cited within: 2]

[34]Geandier G Renault P O Le Bourhis E Goudeau P Faurie D Le Bourlot C Djémia P Castelnau O Chérif S M 2010 Appl. Phys. Lett. 96 041905
DOI:10.1063/1.3293450 [Cited within: 1]

[35]He W Han M D Goudeau P Le Bourhis E Renault P O Wang S B Li L A 2018 Appl. Surf. Sci. 434 771
DOI:10.1016/j.apsusc.2017.09.164 [Cited within: 1]

[36]He W Han M D Wang S B Goudeau P Le Bourhis E Renault P O 2019 Acta Mech. Sin. 35 1210
DOI:10.1007/s10409-019-00885-8 [Cited within: 1]

[37]Schadler L S Noyan I C 1992 J. Mater. Sci. Lett. 11 1067
DOI:10.1007/BF00729763 [Cited within: 1]

[38]Schadler L S Noyan I C 1991 MRS Online Proc. Libr. Arch. 239 p151
DOI:10.1557/PROC-239-151 [Cited within: 1]

[39]Dai Z H Hou Y Sanchez D A Wang G R Brennan C J Zhang Z Liu L Q Lu N S 2018 Phys. Rev. Lett. 121 266101
DOI:10.1103/PhysRevLett.121.266101 [Cited within: 1]

[40]Zhao H Min K Aluru N R 2009 Nano Lett. 9 3012
DOI:10.1021/nl901448z [Cited within: 1]

[41]Javid A Raza N Osman M S 2019 Commun. Theor. Phys. 71 362
DOI:10.1088/0253-6102/71/4/362 [Cited within: 1]

[42]Rappe A K Casewit C J Colwell K S Goddard W A Skiff W M Uff A 1992 J. Am. Chem. Soc. 114 10024
DOI:10.1021/ja00051a040 [Cited within: 1]

[43]Menéndez J Singh R Drucker J 2011 Ann. Phys. 523 145
DOI:10.1002/andp.201000106 [Cited within: 4]