G Sowmya¹, B J Gireesha^,1, S Sindhu¹, B C Prasannakumara²¹Department of PG Studies and Research in Mathematics, Kuvempu University, Shankaraghatta-577 451, Karnataka, India
²Department of Mathematics, Davangere University, Davangere-577002, Karnataka, India

Received:2019-09-5Revised:2019-11-1Accepted:2019-12-23Online:2020-02-05


Abstract
The thermal attributes of porous fin due to radiation and natural convection have been carried out in the presence of nanofluid flow. The geometry of the fin taken for the analysis is rectangular profiled longitudinal fin. The temperature-dependent internal heat generation condition is also considered along with Darcy’s model. The two types of nanofluid containing titanium alloy (${Ti}6{Al}4V$) and aluminium alloy (AA7075) immersed in water is considered for the investigation. The modelled nonlinear ordinary differential equation is numerically solved by the Runge–Kutta–Fehlberg technique. The impact of geometric parameter on the heat transfer analysis of the fin due to the flow of both nanofluids is plotted and consequences are physically interpreted. It is observed that the presence of the water-based titanium alloy better enhances the fin heat transfer rate.
Keywords： alloys;nanofluid;porous fin;heat transfer analysis;convective condition;internal heat generation


PDF (1202KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
G Sowmya, B J Gireesha, S Sindhu, B C Prasannakumara. Investigation of Ti6Al4V and AA7075 alloy embedded nanofluid flow over longitudinal porous fin in the presence of internal heat generation and convective condition. Communications in Theoretical Physics, 2020, 72(2): 025004- doi:10.1088/1572-9494/ab6904

1. Introduction

Due to the wide range of applications of nanofluid in the field of heat exchangers, solar collectors, electrical cooling systems, biomedicines etc., the heat management using nanofluids is one of the trending topics of research. The nanoparticles considered for the nanofluid preparation may be polymeric, semiconductor, metal, ceramic, or carbon based etc. The proper composition of metals gives rise to alloys of greater strength or resistance. The suspension of alloy as a nano-sized particle in the base fluid can be used as nanofluid. In this regard, Zitnansky and Caplovic [1] obtained that thermal and mechanical treatment enabled them to produce an alloy with microstructure. Aminfar et al [2] numerically examined the hydro thermal properties of ferrofluid. Experimental analysis on thermal conductivity and dynamic viscosity of ${Ag}-{MgO}/{H}_{2}O$ hybrid nanofluid has been carried out by Esfe et al [3]. Experimental study on the mechanical properties of copper alloy has been studied by Nassar et al [4]. Superplasticity in Ti6Al4V has been studied experimentally by Alabort et al [5]. They found that after long deformation, microstructure remains equiaxed. Mahmoodi and Kandelousi [6] examined the kerosene-alumina nanoliquid flow in the semi cryogenic engine channel. Farooq et al [7] considered non-Darcy porous medium to scrutinize the squeezed nanoliquid flow. TiO₂-ethylene glycol nanofluid flow in a stretching surface was analysed by Hosseinzadeh et al [8]. MHD Couettee-Poiseuille flow of nanofluids in a rotating channel was discussed by Tlili et al [9] and they revealed that entropy generation rate diminishes for nanofluid parameter due to mass and heat transfer. Makinde et al [10] described the influence of AA7075 and ${Ti}6{Al}4V$ nanoparticles on fluid flow across a rotating disk. The finite element method based on the control volume is utilized by Sheikholeslami et al [11] to analyse the nanofluid free convection in the presence of electric field. Shashikumar et al [12] have investigated the influence of the alloy nanoparticle on the fully developed stream of nanofluid in a microchannel. Rakesh et al [13] have done the comparative study between the slip nanofluid flow and no-slip nanofluid flow in the existence of viscous dissipation and Joule heating. They showed that heat transfer rate is significantly controlled by velocity slip and temperature jump. By applying the homotopy perturbation method, Abbasi et al [14] have examined the peristalsis of nanofluid in the presence of Hall effect and ohmic heating, whereas Abbasi et al [15] extended the work for temperature-dependent viscosity and they graphically discussed the Bejar number and entropy generation.

Another method in enhancing heat transport rate is by considering fin structure. Fin has a wide range of applications in electrical chips, air conditioner, automobile, refrigeration, air cooled craft engines, vehicle radiators etc. Hence, Kiwan and Nirm [16] have investigated the performance of permeable fin in the improvement of heat transport rate. The comparative study between solid convectional fin and porous fin is carried out and found that porous fin displays better performance. Kiwan [17] also carried out the study of porous fin under natural convection conditions and analysed the performance of finite length fin and infinite long fin. Sharqawy and Zubair [18] have analytically examined the mass and heat transfer phenomena of straight fin and comprehensively presented the optimization as well as efficiency of fin. In addition to the convection, radiation also affects the heat transport phenomenon. Hence, Gorla and Bakier [19] have examined the radiation and natural convection condition on permeable fin and proved that fin with radiation transfer extra heat than fin without radiation. Aziz and Khani [20] developed an analytical solution to solve a physical problem of moving fin under variable thermal conductivity condition applying the homotopy analysis method (HAM). Darvishi et al [21] also used the HAM method to solve the problem on permeable fins under radiation as well as the natural convection condition. Darvishi et al [22] have extended the earlier study by considering porous fin’s unsteady thermal response.

The study of fin efficiency and temperature performance is carried out under variable thermal conductivity and the generation of th eheat condition by Aziz and Bouaziz [23] by applying the least square method. Hatami et al [24] have carried out the analysis by considering different fin materials like Al and ${{Si}}_{3}{N}_{4}$. Ghasemi et al [25] have utilized the differential transform method to examine fin performance in the presence of generation of heat internally. The fin of concave, triangular, convex and rectangular profiles were taken for the investigation by Mosayebidorcheh et al [26] and analysed the thermal behaviour using the hybrid method. Sobamowo [27] have taken rectangular fin for analysis and applied the finite difference method.

The wet condition around the fin surface improves the exchange of heat. Therefore, Hatami et al [28] have focused on the investigation of fully wet fin of the semi spherical profile under permeable nature and determined its refrigerator efficiency. Hatami and Ganji [29] have discussed mass and heat transfer analysis from circular fin under fully wet conditions. Vahabzadeh [30] have performed the analytical study on fully wet pin fin by applying the least square method. The variable heat generation and conductivity in the moving fin is described analytically utilizing the DTM method by Dogonchi and Ganji [31]. Furthermore, Darvishi et al [32] have utilized the Spectral Collocation technique to explain the performance of longitudinal fin under wet conditions. Gireesha et al [33] have developed the finite element method to examine wetted moving fin of the radial profile.

Based on the aforementioned literature investigation, we endeavour to combine the heat transfer rate enhancing factors like alloy-embedded nanofluid flow as well as porous fin under wet condition in the presence of natural convection and radiation. The generation of internal heat is considered for the analysis and convective boundary condition is taken for the study. Here, the Runge–Kutta–Fehlberg method is applied and the mathematical study is carried out by graphical interpretation of the obtained results.

2. Mathematical formulation

A flow of nanoliquid over the porous fin under radiation and natural conduction conditions is considered for the analysis. The attached fin to the prime surface is in longitudinal geometry with length L, thickness t and width w and it is displayed in figure 1. The fin base is kept at contact temperature T_b and the temperature of surrounding fluid is T_a. The fin is assumed to be stagnated along with internal heat generation. For the flow of fluid to infiltrate through the porous nature of the fin, Darcy’s model has been taken for the analysis. The small element of the fin dx is considered and a steady state energy balance equation of the present model on dx is(1)$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{{{\rm{d}}}^{2}T}{{{\rm{d}}{x}}^{2}}-\displaystyle \frac{2{F}_{f-a}\varepsilon \sigma }{{{tk}}_{{nf}}}({T}^{4}-{T}_{a}^{4})-\displaystyle \frac{2{Kg}{\left(\rho \beta \right)}_{{nf}}{\left(\rho {C}_{p}\right)}_{{nf}}}{{k}_{{nf}}{\mu }_{{nf}}t}{\left(T-{T}_{a}\right)}^{2}\\ \quad -\,\displaystyle \frac{2(T-{T}_{a})(1-\bar{\phi })h}{{{tk}}_{{nf}}}-\displaystyle \frac{2{i}_{{fg}}{h}_{D}(\omega -{\omega }_{a})(1-\bar{\phi })}{{{tk}}_{{nf}}}\\ \quad +\,\displaystyle \frac{{q}^{* }}{{k}_{{nf}}}=0.\end{array}\end{eqnarray}$Here g is acceleration due to gravity, K is permeability, ϵ is emissivity, ${F}_{f-a}$ is shape factor, i_fg is latent heat of vaporization, $\bar{\phi }$ is porosity and q^* is the generation of internal heat and it is assumed to be a linear function of temperature, defined as [23](2)$\begin{eqnarray}{q}^{* }={q}_{a}^{* }(1+{\varepsilon }_{g}(T-{T}_{a})),\end{eqnarray}$where, ${q}_{a}^{* }$ is heat generated at temperature T_a. The coefficient of convective heat transfer h is defined as [32](3)$\begin{eqnarray}h={\left(\displaystyle \frac{T-{T}_{a}}{{T}_{b}-{T}_{a}}\right)}^{n}{h}_{a},\end{eqnarray}$where, the convective heat transfer at temperature T_a is h_a.

Figure 1.

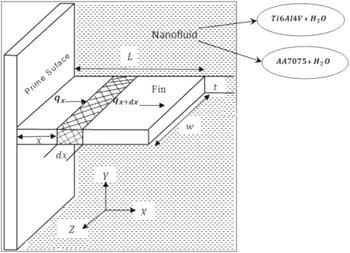New window|Download| PPT slide
Figure 1.Coordinate system of the physical model.


By applying equations (2) and (3), equation (1) reduces to(4)$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{{{\rm{d}}}^{2}T}{{{\rm{d}}{x}}^{2}}-\displaystyle \frac{2{F}_{f-a}\varepsilon \sigma }{{{tk}}_{{nf}}}({T}^{4}-{T}_{a}^{4})-\displaystyle \frac{2{Kg}{\left(\rho \beta \right)}_{{nf}}{\left(\rho {C}_{p}\right)}_{{nf}}}{{k}_{{nf}}{\mu }_{{nf}}t}{\left(T-{T}_{a}\right)}^{2}\\ \quad -\,\displaystyle \frac{2{h}_{a}{\left(T-{T}_{a}\right)}^{n+1}(1-\bar{\phi })}{t{\left({T}_{b}-{T}_{a}\right)}^{n}{k}_{{nf}}}-\displaystyle \frac{2{i}_{{fg}}{h}_{D}(\omega -{\omega }_{a})(1-\bar{\phi })}{{{tk}}_{{nf}}}\\ \quad +\,\displaystyle \frac{{q}_{a}^{* }(1+{\varepsilon }_{g}(T-{T}_{a}))}{{k}_{{nf}}}=0.\end{array}\end{eqnarray}$

Further, the nanoparticle of titanium alloy (${Ti}6{Al}4V$) and aluminium alloy (AA7075) with base fluid water are in thermal equilibrium state. The nanoparticle AA7075 contains 90% Al, 5%–6% Zn, 2%–3% Mg, 1%–2% Cu and less than a half percent of other metals. ${Ti}6{Al}4V$ is made up of 90% Ti, 6% Al, 4% V, 0.25% Fe and less than a half percent of other metals. The thermophysical quantities like thermal conductivity (k), coefficient of thermal expansion (β), specific heat (C_p), density (ρ) and dynamic viscosity (μ) of the nanofluid are as presented in table 1. These thermophysical properties are modelled via mixture theory. They are as follows:(5)$\begin{eqnarray}\displaystyle \frac{{k}_{{nf}}}{{k}_{f}}=\displaystyle \frac{(2{k}_{f}+{k}_{s})+2\phi ({k}_{s}-{k}_{f})}{(2{k}_{f}+{k}_{s})-\phi ({k}_{s}-{k}_{f})},\end{eqnarray}$(6)$\begin{eqnarray}{\left(\rho {C}_{p}\right)}_{{nf}}=\phi {\left(\rho {C}_{p}\right)}_{s}+(1-\phi ){\left(\rho {C}_{p}\right)}_{f},\end{eqnarray}$(7)$\begin{eqnarray}{\left(\rho \beta \right)}_{{nf}}=\phi {\left(\rho \beta \right)}_{s}+(1-\phi ){\left(\rho \beta \right)}_{f},\end{eqnarray}$(8)$\begin{eqnarray}{\rho }_{{nf}}=\phi {\rho }_{s}+(1-\phi ){\rho }_{f},\end{eqnarray}$(9)$\begin{eqnarray}{\mu }_{{nf}}=\displaystyle \frac{{\mu }_{f}}{{\left(1-\phi \right)}^{2.5}},\end{eqnarray}$where, φ is nanoparticle volume fraction and the subscript nf, s and f denotes nanofluid, nanoparticle and base fluid respectively.


Table 1.
Table 1.Thermophysical properties of water, Ti6Al4V and AA7075 [10].

Physical properties	$k(W/{mk})$	${C}_{p}(j/{kgk})$	$\rho ({kg}/{m}^{3})$	$\beta \times {10}^{5}(1/K)$
Water	0.613	4179	997.1	21
${Ti}6{Al}4V$	7.2	0.56	4420	0.86
AA7075	173	960	2810	2.34

New window|CSV

The following dimensionless variables are considered:(10)$\begin{eqnarray}\begin{array}{rcl}\theta & = & \displaystyle \frac{T}{{T}_{b}},\,{\theta }_{a}=\displaystyle \frac{{T}_{a}}{{T}_{b}},\,X=\displaystyle \frac{x}{L},\\ {Nc} & = & \displaystyle \frac{2g{\left(\rho \beta \right)}_{f}K{\left(\rho {C}_{p}\right)}_{f}{T}_{b}{L}^{2}}{{\mu }_{f}{k}_{f}t},{Nr}=\displaystyle \frac{2{F}_{f-a}\varepsilon \sigma {L}^{2}{T}_{b}^{3}}{{{tk}}_{f}},\\ (\omega -{\omega }_{a}) & = & (T-{T}_{a}){b}_{2},{m}_{0}=\displaystyle \frac{2{h}_{a}{L}^{2}(1-\bar{\phi })}{{{tk}}_{f}},\\ {m}_{1} & = & \displaystyle \frac{{h}_{a}{i}_{{fg}}(1-\bar{\phi }){b}_{2}{L}^{2}}{{k}_{f}{{tC}}_{{pf}}{{Le}}^{2/3}},\,{Bi}=\displaystyle \frac{{h}_{a}L}{{k}_{f}},\\ G & = & \displaystyle \frac{{L}^{2}{q}_{a}^{* }}{{k}_{f}{T}_{b}},\,{\varepsilon }_{G}={T}_{b}{\varepsilon }_{g},\,{m}_{2}={m}_{0}+{m}_{1}.\end{array}\end{eqnarray}$Applying equations (5)–(10) into equation (4), we get(11)$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{{{\rm{d}}}^{2}\theta }{{{\rm{d}}{X}}^{2}}-{Nr}({\theta }^{4}-{\theta }_{a}^{4})\left(\displaystyle \frac{2{k}_{f}+{k}_{s}-\phi ({k}_{s}-{k}_{f})}{2{k}_{f}+{k}_{s}+2\phi ({k}_{s}-{k}_{f})}\right)\\ \quad -\,{m}_{2}\displaystyle \frac{{\left(\theta -{\theta }_{a}\right)}^{n+1}}{{\left(1-{\theta }_{a}\right)}^{n}}\left(\displaystyle \frac{2{k}_{f}+{k}_{s}-\phi ({k}_{s}-{k}_{f})}{2{k}_{f}+{k}_{s}+2\phi ({k}_{s}-{k}_{f})}\right)\\ \quad -\,{Nc}{\left(\theta -{\theta }_{a}\right)}^{2}\displaystyle \frac{\left(\tfrac{\phi {\rho }_{s}{\left(\beta \right)}_{s}}{{\rho }_{f}{\left(\beta \right)}_{f}}+(1-\phi \right)\left(\tfrac{\phi {\rho }_{s}{\left({C}_{p}\right)}_{s}}{{\rho }_{f}{\left({C}_{p}\right)}_{f}}+(1-\phi \right)}{\left(\tfrac{1}{{\left(1-\phi \right)}^{2.5}}\right)\left(\tfrac{2{k}_{f}+{k}_{s}+2\phi ({k}_{s}-{k}_{f})}{2{k}_{f}+{k}_{s}-\phi ({k}_{s}-{k}_{f})}\right)}\\ \quad +\,G(1+{\varepsilon }_{G}(\theta -{\theta }_{a}))\left(\displaystyle \frac{2{k}_{f}+{k}_{s}-\phi ({k}_{s}-{k}_{f})}{2{k}_{f}+{k}_{s}+2\phi ({k}_{s}-{k}_{f})}\right)=0.\end{array}\end{eqnarray}$The subsequent dimensionless convective boundary conditions are:(12)$\begin{eqnarray}\begin{array}{rcl} & & X=0,\,\theta =1,\\ & & X=1,\,\displaystyle \frac{{\rm{d}}\theta }{{\rm{d}}{X}}=-\displaystyle \frac{{k}_{f}}{{k}_{{nf}}}{Bi}\theta (1).\end{array}\end{eqnarray}$In the above equations, $\theta ,{Nr},{m}_{2},{Nc},G,{\theta }_{a},n,{\varepsilon }_{G}$ and Bi are dimensionless temperature, radiative parameter, wet porous parameter, convective parameter, generation number, ambient fluid, power index, dimensionless internal heat generator and Biot number correspondingly.

3. Numerical procedure

The nonlinear ordinary differential equation (11) is integrated by using the Runge–Kutta–Fehlberg technique with shooting scheme. The primary thought of the shooting scheme is to get an initial value problem by restructuring the boundary value problem. Then, the obtained IVP is simplified by the Runge–Kutta–Fehlberg technique. This technique employs a pair of Runge-Kutta methods, which is of the 4th order and 5th order. Among them, the 4th order scheme is used to propagate the solution and 5th order method for error control. Both relative and absolute error tolerances pertain for this technique. The solution of reframed IVP provides the solution to initial BVP. In present numerical calculations, the convergence criteria is 10⁻⁶ with step size 0.001.

4. Results and discussion

In order to scrutinize the salient feature of temperature field for diverse values of relevant parameters, a numerical analysis is carried out by the Runge–Kutta–Felhberg method. The numerical results for both the alloys are represented in figures 2–12.

Figure 2.

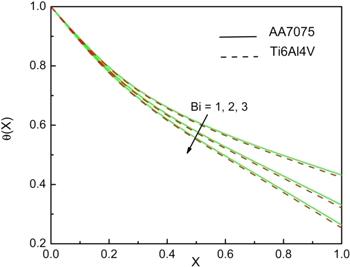
New window|Download| PPT slide
Figure 2.Impact of Bi on the temperature performance of the fin when G=0.1, Nc=10, Nr=5, m₂=1, ϵ_G=0.2, θ_a=0.4, and n=1.


Figure 2 shows the impact of the Biot number on the thermal profile along fin length for ${AA}7075-{H}_{2}O$ and ${Ti}6{Al}4V-{H}_{2}O$ nanofluid. It is noticed that, with the increase in Bi from 1 to 3, the temperature of the fin decreases. Physically, Biot number is proportional to convection at the surface and inversely proportional to conduction within the surface. Hence, convective heat transfer intensifies for higher values of Bi. Additionally, water-based titanium alloy nanofluid displays relatively more heat transfer than aluminium alloy nanofluid.

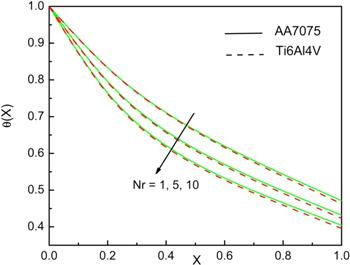
The influence of variation of radiative parameter on the temperature field of the fin for ${AA}7075-{H}_{2}O$ and ${Ti}6{Al}4V-{H}_{2}O$ nanofluid is as depicted in figure 3. It is clearly visible that, as the Nr value amplifies, temperature of the fin reduces. This is due to the fact that increase in Nr means enhancement in the radiation effect, which decreases the fin temperature. Hence, radiation effect impacts on the fin cooling process. Clearly, titanium alloy nanofluid shows lower temperature compared to aluminium alloy nanofluid.

Figure 3.

New window|Download| PPT slide
Figure 3.Impact of Nr on the temperature performance of the fin when G=0.1, Nc=10, m₂=1, ϵ_G=0.2, θ_a=0.4, n=1, and Bi=1.


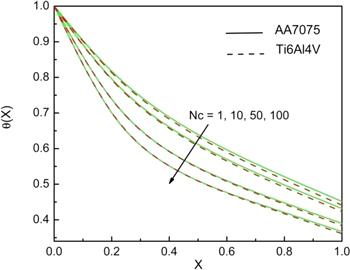
The effect of different values of convective parameter on the fin temperature distribution is as displayed in figure 4. As the convective factor enhances, temperature of the fin decreases. This is because Nc is a product of Rayleigh number and Darcy’s number. With the raise in Nc, Da enhances, which means permeability increases. On the other hand, the increase in Ra leads to a reduction in thermal resistance. Hence, with the enhancement in the convective parameter, transfer of heat from the surface of fin amplifies. At lower Nc value, ${Ti}6{Al}4V$ exhibits a better heat transfer rate but for higher Nc value both the nanofluid presents the same nature.

Figure 4.

New window|Download| PPT slide
Figure 4.Impact of Nc on the temperature performance of the fin when G=0.1, Nr=5, m₂=1, ϵ_G=0.2, θ_a=0.4, n=1, and Bi=1.


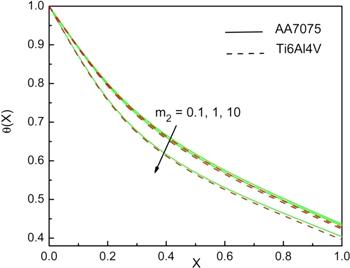
Figure 5 illustrates the influence of wet porous factor on temperature behaviour of fin. It is observed that, as m₂ rises from 0.1 to 1, minute difference is seen, but rise of m₂ from 1 to 10 shows large variation and temperature of the fin decreases rapidly. Since, the permeable nature of fin assists in the flow of fluid to penetrate through it. Hence, we notice more heat transfer rate. Additionally, for a higher m₂ value, titanium alloy displays relatively more heat transfer than aluminium alloy nanofluid.

Figure 5.

New window|Download| PPT slide
Figure 5.Impact of m₂ on the temperature performance of the fin when G=0.1, Nc=10, Nr=5, ϵ_G=0.2, θ_a=0.4, n=1, Bi=1.


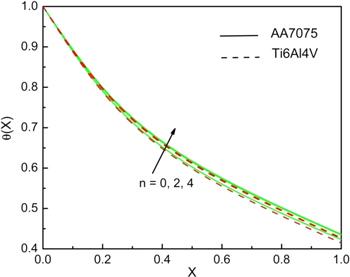
The impact of power index (n) on the thermal profile of the fin with flow of titanium and aluminium alloy embedded nanofluid is plotted in figure 6. As the n rises from 0 to 4, there will be more thermal profile. The different n values depict the different flow natures. It is clear observed that n=0 represents the linear case and n>0 presents the nonlinear case.

Figure 6.

New window|Download| PPT slide
Figure 6.Impact of n on the temperature performance of the fin when G=0.1, Nc=10, Nr=5, m₂=1, ϵ_G=0.2, θ_a=0.4, and Bi=1.


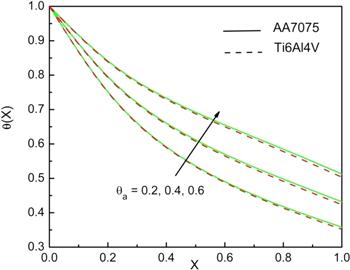
The influence of ambient temperature on thermal behaviour of the fin is as explored in figure 7. It is found that the thermal profile is an increasing function of ambient temperature. This is because of the increase in surrounding fluid temperature, heat transfer from fin decreases. The aluminium alloy nanofluid shows more temperature of the fin compared to titanium alloy nanofluid.

Figure 7.

New window|Download| PPT slide
Figure 7.Impact of θ_a on the temperature performance of the fin when G=0.1, Nc=10, Nr=5, m₂=1, ϵ_G=0.2, n=1, and Bi=1.


Figure 8 reveals the influence of generation number on the fin thermal field. An increase in fin temperature for higher values of the generation number is noticed. The generation of internal heat within the fin, leads to a rise in temperature of the fin surface. Hence, transfer of heat diminishes. In addition, ${Ti}6{Al}4V$ exhibits relatively more heat transfer than AA7075.

Figure 8.

New window|Download| PPT slide
Figure 8.Impact of G on the temperature performance of the fin when Nc=10, Nr=5, m₂=1, ϵ_G=0.2, θ_a=0.4, n=1, Bi=1.


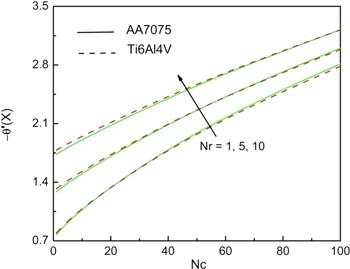
The effect of simultaneous variation in radiative and convective parameter on the thermal gradient at the base point is as shown in figure 9. It is noticed that thermal gradient is more for larger values of radiative and convective parameter for both titanium and aluminium alloy nanofluid. The thermal gradient variation due to simultaneous change in generation number and internal heat generation parameter is analysed from figure 10. Clearly, the gradient decreases as the G and ϵ_G increases. Hence, the generation of internal heat negatively affects the fin rate of heat transfer. It is also observed that ${Ti}6{Al}4V$ alloy displays a higher gradient than the AA7075 alloy.

Figure 9.

New window|Download| PPT slide
Figure 9.Influence of Nc and Nr on the temperature gradient at fin base when G=0.1, m₂=1, ϵ_G=0.2, θ_a=0.4, n=1, and Bi=1.

Figure 10.

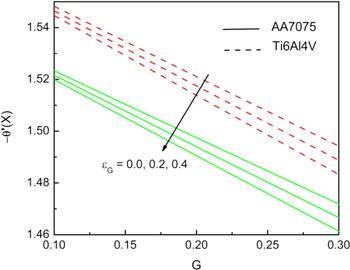New window|Download| PPT slide
Figure 10.Influence of ϵ_G and G on the temperature gradient at the fin base when Nc=10, Nr=5, m₂=1, θ_a=0.4, n=1, and Bi=1.


Figure 11 presented the influence of combined wet porous parameter and Biot number on the fin temperature gradient for both the nanofluids. Here, with the increase in m₂ and Bi, the gradient keeps on increasing. It is also noticed that, for larger m_2, more gradient effect is observed and also heat transfer due to the titanium alloy being better than the aluminium alloy. The impact of ambient temperature and power index on the thermal gradient variation at the fin base is as plotted in figure 12. The gradient is a decreasing function, for increase in power index as well as ambient temperature for both water-based titanium and aluminium alloy.

Figure 11.

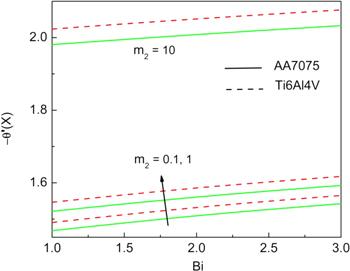New window|Download| PPT slide
Figure 11.Influence of m₂ and Bi on the temperature gradient at the fin base when G=0.1, Nc=10, Nr=5, ϵ_G=0.2, θ_a=0.4, and n=1.

Figure 12.

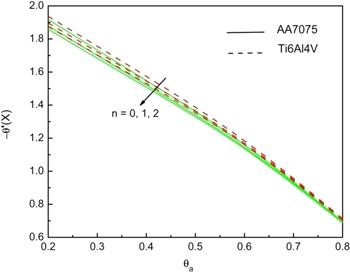New window|Download| PPT slide
Figure 12.Influence of n and θ_a on the temperature gradient at the fin base when G=0.1, Nc=10, Nr=5, m₂=1, ϵ_G=0.2, and Bi=1.

5. Conclusion

The transfer of heat through longitudinal porous fin wetted with nanofluid of ${Ti}6{Al}4V$ and AA7075 alloy immersed in base water is examined in the existence of natural convection and radiation condition along with convective boundary condition and the generation of internal heat. From the current analysis, the following conclusions are drawn:•The radiation and convection characteristics showed a significant effect on the rate of heat transfer.
•The wet porous nature of the fin enhances the heat transfer rate.
•The internal heat generation negatively affects the fin cooling procedure.
•The presence of nanofluid favors the heat transfer phenomenon.
•The ambient temperature and power index increases temperature field and as a result decreases the heat transfer rate.
•Both titanium and aluminum alloy nanofluid enhances the temperature gradient.
•It is found that the ${Ti}6{Al}4V-{H}_{2}O$ nanofluid is better in enhancing heat transfer from the fin surface compared to ${AA}7075-{H}_{2}O$ nanofluid.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Zitnansky M Caplovic L 2004 J. Mat. Proc. Tech. 157 643
DOI:10.1016/j.jmatprotec.2004.07.151 [Cited within: 1]

[2]Aminfar H Mohammadpourfard M Mohseni F 2012 J. Mag. Mag. Mat. 324 830
DOI:10.1016/j.jmmm.2011.09.028 [Cited within: 1]

[3]Esfe M H Arani A A A Rezaie M Yan W M Karimipour A 2015 Int. Commu. Heat Mass Transfer 66 189
DOI:10.1016/j.icheatmasstransfer.2015.06.003 [Cited within: 1]

[4]Nassar A A Jarrad A N 2015 Int. J. Current Eng. Tech. 5 2582
DOI:10.17605/OSF.IO/WHTZV [Cited within: 1]

[5]Alabort E Putman D Reed R C 2015 Acta Mater. 95 428
DOI:10.1016/j.actamat.2015.04.056 [Cited within: 1]

[6]Mahmoodi M Kandelousi S 2015 Nuclear Eng. Design 291 277
DOI:10.1016/j.nucengdes.2015.05.022 [Cited within: 1]

[7]Farooq M Ahmad S Javed M Anjum A 2019 J. Heat Transfer 141 012402
DOI:10.1115/1.4041497 [Cited within: 1]

[8]Hosseinzadeh K Afsharpanah F Zamani S Gholinia M Ganji D D 2018 Case Studies Therm. Eng. 12 228
DOI:10.1016/j.csite.2018.04.008 [Cited within: 1]

[9]Tlili I Hamadneh N N Khan W A Atawneh S 2018 J. Therm. Anal. Calorim. 132 1899
DOI:10.1007/s10973-018-7066-5 [Cited within: 1]

[10]Makinde O D Mahanthesh B Gireesha B J Shashikumar N S Monaledi R L Tshehla M S 2018 Defect Diffus. Forum 384 69
DOI:10.4028/www.scientific.net/DDF.384.69 [Cited within: 2]

[11]Sheikholeslami M Shehzad S A Kumar R 2018 Commun. Theor. Phys. 69 667
DOI:10.1088/0253-6102/69/6/667 [Cited within: 1]

[12]Shashikumar N S Gireesha B J Mahanthesh B Prasannakumara B C Chamkha A J 2019 Int. J. Num. Methods Heat Fluid Flow 29 3638
DOI:10.1108/HFF-06-2018-0301 [Cited within: 1]

[13]Kumar R Kumar R Koundal R Shehzad S A Sheikholeslami M 2019 Commun. Theor. Phys. 71 779
DOI:10.1088/0253-6102/71/7/779 [Cited within: 1]

[14]Abbasi F M Shanakhat I Shehzad S A 2019 Phys. Scr. 94 025001
DOI:10.1088/1402-4896/aaf600 [Cited within: 1]

[15]Abbasi F M Shanakhat I Shehzad S A 2019 J. Mag. Mag. Mat. 474 434
DOI:10.1016/j.jmmm.2018.10.132 [Cited within: 1]

[16]Kiwan S Al-Nimr M A 2001 J. Heat Transfer 123 790
DOI:10.1115/1.1371922 [Cited within: 1]

[17]Kiwan S 2007 Trans. Porous Media 67 17
DOI:10.1007/s11242-006-0010-3 [Cited within: 1]

[18]Sharqawy M H Zubair S M 2008 Applied Therm. Eng. 28 2279
DOI:10.1016/j.applthermaleng.2008.01.003 [Cited within: 1]

[19]Gorla R S R Bakier A Y 2011 Int. Commun. Heat Mass Transfer 38 638
DOI:10.1016/j.icheatmasstransfer.2010.12.024 [Cited within: 1]

[20]Aziz A Khani F 2011 J. Franklin Institute 348 640
DOI:10.1016/j.jfranklin.2011.01.008 [Cited within: 1]

[21]Darvishi M T Gorla R S R Khani F 2013 Int. J. Num. Methods Heat Fluid Flow 23 1406
DOI:10.1108/HFF-12-2011-0264 [Cited within: 1]

[22]Darvishi M T Gorla R S R Khani F 2014 Heat Mass Transfer 50 1311
DOI:10.1007/s00231-014-1341-1 [Cited within: 1]

[23]Aziz A Bouaziz M N 2011 Energy Convers. Manag. 52 2876
DOI:10.1016/j.enconman.2011.04.003 [Cited within: 2]

[24]Hatami M Hasanpour A Ganji D D 2013 Energy Convers. Manag. 74 9
DOI:10.1016/j.enconman.2013.04.034 [Cited within: 1]

[25]Ghasemi S E Hatami M Ganji D D 2014 Case Studies Therm. Eng. 4 1
DOI:10.1016/j.csite.2014.05.002 [Cited within: 1]

[26]Mosayebidorcheh S Farzinpoor M Ganji D D 2014 Energy Convers. Manag. 86 365
DOI:10.1016/j.enconman.2014.05.033 [Cited within: 1]

[27]Sobamowo M G 2016 Alexandria Eng. J. 56 1
DOI:10.1016/j.aej.2016.04.022 [Cited within: 1]

[28]Hatami M Ahangar G H R M Ganji D D Boubaker K 2014 Energy Conver. Manag. 84 533
DOI:10.1016/j.enconman.2014.05.007 [Cited within: 1]

[29]Hatami M Ganji D D 2014 Int. J. Refrig. 40 140
DOI:10.1016/j.ijrefrig.2013.11.002 [Cited within: 1]

[30]Vahabzadeh A Ganji D D Abbasi M 2015 Case Studies Therm. Eng. 5 1
DOI:10.1016/j.csite.2014.11.002 [Cited within: 1]

[31]Dogonchi A S Ganji D D 2016 Applied Therm. Eng. 103 705
DOI:10.1016/j.applthermaleng.2016.04.121 [Cited within: 1]

[32]Darvishi M T Gorla R S R Khani F Gireesha B J 2016 Int. J. Num. Methods Heat Fluid Flow 26 2419
DOI:10.1108/HFF-06-2015-0230 [Cited within: 2]

[33]Gireesha B J Sowmya G Macha M 2019 Int. J. Num. Methods Heat Fluid Flow
DOI:10.1108/HFF-12-2018-0744 [Cited within: 1]