Aisha Anjum, N. A. Mir, M. Farooq^,*, M. Javed^*, S. Ahmad^*Department of Mathematics, Riphah International University, Islamabad 44000, Pakistan

Corresponding authors: * E-mail:hfarooq99@yahoo.com

Received:2018-08-8Online:2019-04-1


Abstract
This article scrutinizes the features of viscous dissipation in the stagnation point flow past through a linearly stretched Riga wall by implementing Cattaneo-Christov heat flux model. Viscous dissipation is carried out in Cattaneo-Christov diffusion analysis for the first time in this letter. As a result of Cattaneo-Christov model, some extra terms of viscous dissipation are appeared in the energy equation. These extra terms of viscous dissipation are missing in the literature. On the utilization of suitable transformations, the equations governing the problem are reduced under the boundary layer approximation into the non-linear and dimensionless ordinary differential equations. Convergent approach is utilized to solve the dimensionless governing equations. The solution thus acquired is used to highlight the effects of emerging parameters on velocity distribution and fluid's temperature through the graphs. Features of the drag force (or skin friction co-efficient) are graphically interpreted. It is noticed that the presence of modified Hartman number helps to reduce the fluid's temperature but enhances the velocity profile. Further an enlargement in the value of thermal time relaxation parameter helps to decrease the temperature distribution.
Keywords： stagnation point;Cattaneo-Christov theory;Riga plate;linear stretching;viscous dissipation


PDF (872KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Aisha Anjum, N. A. Mir, M. Farooq, M. Javed, S. Ahmad. Investigations of Viscous Dissipation in Stagnation Point Flow Past a Stretchable Riga Wall: Modern Analysis of Heat Transport. [J], 2019, 71(4): 377-383 doi:10.1088/0253-6102/71/4/377

1 Introduction

The flows in the stagnation point region have significantly appeared in the field of fluid mechanics which can be explored as inviscid or viscous, two-dimensional or three-dimensional, symmetric or asymmetric, steady (or unsteady) and in many other ways. The flow mechanism focusing on the stagnation point flows has extended its importance both in industrial and natural processes. Therefore, stagnation point flows have still attracted the researchers and engineers after its various useful practical applications include the cooling process of nuclear reactors in case of emergency shutdown, in engineering domian we have hydrodynamic processes, cooling of electronic devices, cooling process of matallic infinite plate in bath and magneto-hydrodynamic (MHD) generators, metallurgical processes like tinning of copper wires, annealing and drawing. Thus, different aspects of flows in stagnation point region have been examined by the researches. Weidman and Turner^[1] explored the features of stagnation flow through a stretchable surface. The region around the stagnation point where the flow is due to exponential stretching of cylinder is exposed by Merkin it et al.^[2] Borrelli it et al.^[3] explored the 3D flow of the magneto viscous fluid in the region of stagnation-point with buoyancy effects. Agbaje it et al.^[4] disclosed the magnetic field effects on stagnation-point flow deformed by stretchable sheet. Sharma it et al.^[5] analyzed the features of heat absorption (or generation) on MHD stagnant flow passing from stretchable vertical surface having mixed convection effects. Features of magnetohydrodynamic (MHD) on stagnation-point flow over porous stretchable sheet are investigated by Bhatti it et al.^[6]

Heat produced via dissipation processes are important factor in designing numerous devices. The ability of the velocity against viscous forces to do work is termed as viscous dissipation whereas Cattaneo-Christov model is a hyperbolic type of expression illustrating the transfer of heat in a normal way as like a propagation of waves. Viscous dissipation has pivotal role in connection with various devices, which operate at high deceleration or which are subjected to larger rotating speed and also in processes where gravitational field is strong enough on a large scale, in nuclear engineering related to cooling of reactor and in geological process. Cattaneo-Christov model is devoted to overcome the deficiency in the classical law of heat flux. Fourier's law reflects the parabolic behavior, which explains the transfer of heat in infinite speed throughout the material but it is unrealistic approach. Thus, Cattaneo^[7] was the first how adding the time relaxation factor to fulfill such void in the conventional law of heat flux. Then Christov^[8] implied the time derivative model to attain desire formulation for material -- invariant. Hayat it et al.^[9] studied stagnant flow chracterized via non-Fourier heat flux on non-linear thicked stretchable sheet with auto-catalyst and reactant. Hayat it et al.^[10] disclosed the physical aspects of heat flux upon stratified stretching sheet with Cattabeo-Christov theory. Zubair it et al.^[11] constructed the characteristics of non-Fourier diffusion in flow of thixotropic fluid with non-linear convection. Khan it et al.^[12] examined the dissipation effects in stagnation flow of magneto fluid with autocatalyst and reactants. Hussain it et al.^[13] enclosed the characteristics of viscous dissipation in hydromagneto Sisko nanoliquid flow with Joule heating over stretchable cylinder. Waqas it et al.^[14] scritinized the behavior of Cattaneo-Christov model in the nonlinear convective flow of third grade fliud.

Properities of magneto-hydrodynamic flow of fluid have an impactful role in the development of numerous biomedical, industrial, and engineering processes. The development of these processes comprises of heating and cooling systems, nuclear reactors design, blood flow measurement, MHD generators etc. Electromagnetic body forces are applied to control the flow of fluid, which is electrically conducting and consequently overcome the shortfall of momentum in the boundary layer region. Higher intensity of fluid's electrical conductivity are affected (or influenced) only exposed to external magnetic field of approximately one Tesla. This concept is used in classical magnetohydrodynamic flows. In weekly electrically conducting fluid, external magnetic field is alone not enough to produce currents. Thus, in order to achieve efficient and higher flows control, electric field should be applied externally to generate wall-parallel Lorentz force. Electromagnetic actuator is also termed as Riga plate which is the combination of electrodes and permanent magnets situated on a plane surface is implemented to produce wall-parallel Lorentz force. As an efficient agent, it is utilized to decay the pressure drag and skin friction in the tips of submarines by opposing the boundary layer seperation. Analysis of nanomaterial flow due to Riga plate is disclosed by Ahmed it et al.^[15] Properties of nanoliquid flow over a variable thick Riga plate are analyzed by Hayat it et al.^[16] Farooq it et al.^[17] disclosed the features of melting heat transfer in stagnation flow of viscous fluid towards a variable thick Riga plate. The study of chemically reactive squeezing flow on a Riga plate using convective conditions is done by Hayat it et al.^[18] Ahmad it et al.^[19] investigated the convective heat transport through flow of nanoliquid past over a Riga plate with Buoyancy effects. Naseem it et al.^[20] depicted a concept of two-dimensional flow of third grade nanofluid over stretchable Riga plate utilizing modified laws of Fourier and Fick. Shah it et al.^[21] examined the variable fluid properties using non-Fourier heat flux on stagnation flow through variable thick Riga plate. Qureshi it et al.^[22] explored the features of variable mass diffusivity and thermal conductivity for the fluid flows.

It is evident from the literature survey that not single attempt is available up till now regarding phenomenon of viscous dissipation under Cattaneo-Christov theory. This analysis is also motivated with Riga plate for the first time. Here our main objective is to fulfill such void. In the present work we describe the study of the flow in the region of stagnation-point past through a linear stretchable Riga plate. Cattaneo-Christov diffusive model is adopted to disclose the heat transport phenomena with the incorporation of viscous dissipation. The governing equations are transmuted into a set of non-dimensional forms. Homotopic technique^[23-30] is utilized to calculate the series solution of the flow problem. The acquired results are then utilized to examine the pertinent parameters of interest graphically. Drag force (skin friction co-efficient) are graphed and analyzed.

2 Problem Formulation

Here we consider that flow analysis provides a region, which relates stagnation point to rheological variables and geometrical parameters. Further we consider the case where the fluid moves over a Riga plate, which is linearly stretched in its own plane and consequently deformation occurs. The cartesion co-ordinate system $(x,y)$ is utilized in such a way that the $% x$-axis is taken along the stretching plate and $y$-direction is normal to it. The Cattaneo-Christov theory instead of classical Fourier law is incorporated to analyze the heating effects on heat transfer of viscous fluid. Extra heating factor like viscous dissipation is accounted in energy equation. The wall temperature is assumed lower than ambient fluid temperature. A geometry of the flow problem is illustrated in Fig. 1.

Fig. 1

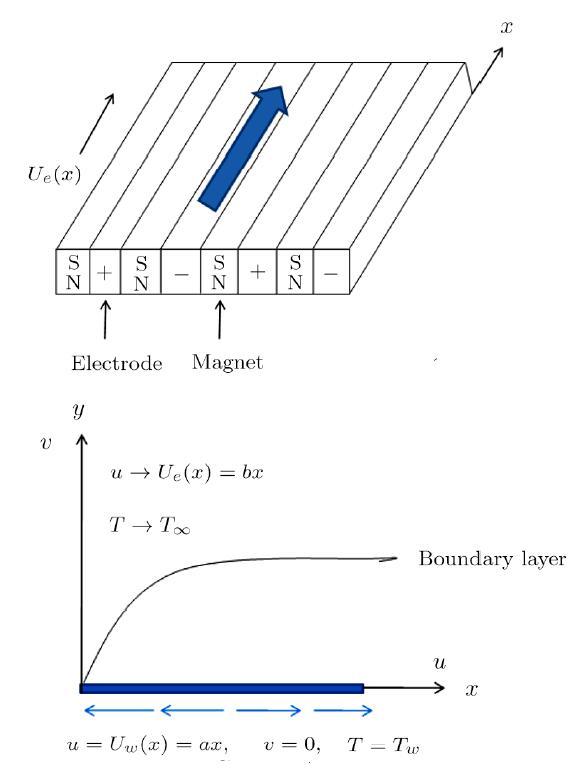New window|Download| PPT slide
Fig. 1(a) Structure of Riga plate. (b) Geometry of flow problem.



Two-dimensional velocity and temperature fields are defined by

(2)$ { V}=[ u( x,y) ,v( x,y) ,0] \,, T=T(x,y)\,. $

The mathematical expression describing the non-Fourier concept is

(3)$ { q}+\delta _{ E}( { V}\cdot { \nabla}{ q}+( { \nabla} \cdot{ V} ) { q}-{ q}\cdot{ \nabla}{ V}) =-k{ \nabla }T\,, $

the above expression for incompressible fluid takes the form

(4)$ { q}+\delta _{ E}( { V}\cdot{ \nabla}{ q}-{ q}\cdot{ \nabla} V) =-k{ \nabla }T\,. $

In above expression $\delta _{ E}$ denotes the thermal relaxation time, $\% { q}$ represents the heat flux, ${ V}$ denotes the fluid velocity, $k$ denotes thermal conductivity, and $T$ represents fluid's temperature.

The governing equations of continuity, momentum and temperature after applying boundary layer approximation are given as the following,

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\,, (5) $$

$$ u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=U_{e}\frac{\% d U_{e}}{d x}+\upsilon \frac{\partial ^{2}u}{\partial y^{2}}+\frac{\pi j_{0}M}{\% 8\rho }\exp \Big( \frac{-\pi }{a_{1}}y\Big) \,, (6) $$

$$ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+\delta _{ E}\Omega _{E}=\frac{k}{\rho C_{p}}\frac{\partial ^{2}T}{\partial y^{2}}+\% \frac{\mu }{\rho C_{p}}\Big( \frac{\partial u}{\partial y}\Big) ^{2}\,. (7) $$

Here $u$ and $v$ are the velocity components along axes $x$ and $y$ respectively, $U_{e}$ denotes free stream velocity, $\nu $ is kinematic viscosity, $a_{1}$ is the width for electrodes and magnets, $j_{0}$ expresses the applied current density in electrodes, $M\;(=M_{0}x$) is permanent variable magnets magnetization, $\rho $ depicts fluid density, $T$ denotes fluid's temperature, $k$ represents thermal conductivity, $C_{p}$ is specific heat, absolute viscosity is represented by $\mu $ and $\delta _{ E}$ is thermal relaxation time.

In the above expression, the value of $\Omega _{E}$ is examined as

(8)$ \Omega _{E} = u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}+v \frac{\partial v}{\partial y}\frac{\partial T}{\partial y}+u\frac{\partial v }{\partial x}\frac{\partial T}{\partial y}+v\frac{\partial u}{\partial y} \frac{\partial T}{\partial x} \\\ +2uv\frac{\partial ^{2}T}{\partial x\partial y} +u^{2}\frac{\partial ^{2}T}{\partial x^{2}}+v^{2}\frac{\partial ^{2}T}{ \partial y^{2}} \\\ -\frac{\mu }{\rho C_{p}}\Big( 2u\frac{\partial u}{\partial y}\frac{ \partial ^{2}u}{\partial x\partial y}+2v\frac{\partial u}{\partial y}\frac{ \partial ^{2}u}{\partial y^{2}}\Big) \,, $

2.1 Boundary Conditions

$$ u=U_{w}( x) =ax\,, \ \ v=0\,, \ \ T=T_{w}\,,\ \ \ \ {\rm at} \ \ y=0\,, u\rightarrow U_{e}( x) =bx\,, \quad T\rightarrow T_{\infty } \ \ \text{when} \ \ y\rightarrow \infty \,, (9) $$

$U_{w}$ is stretching velocity in $x$ direction, $U_{e}$ is ambient or free stream velocity, $a$, $b$ are dimensional constants, $T_{\infty }$ is the ambient fluid temperature, $T_{w}$ is constant wall temperature.

2.2 Transformation

By the induction of suitable variables given below

(10)$ \eta =y\sqrt{\frac{a}{\upsilon }}\,, \ \ u=axf'(\eta )\,, \ \ v=-\sqrt{a\nu }f(\eta )\,, \theta ( \xi ) =\frac{T-T_{\infty }}{T_{w}-T_{\infty }}\,, $

mass conservation law is satisfied identically, however other conservation laws are simplified as follows:

(11)$ f^{\prime \prime \prime }+ff^{\prime \prime }-(f^{\prime })^{2}+S^{2}+Q\exp ( -B\eta ) =0\,, $

(12)$ \theta ^{\prime \prime }+Pr f\theta ^{\prime }+Pr Ec(f^{\prime \prime })^{2}-Pr \gamma ( ff^{\prime }\theta ^{\prime }+( f) ^{2}\theta ^{\prime \prime }) \quad +2Pr \gamma Ec( f^{\prime }(f^{\% \prime \prime })^{2}-ff^{\prime \prime }f^{\prime \prime \prime }) =0\,, $

with boundary conditions:

(13)$ f(0)=0\,, \quad f^{\prime }(0)=1\,, \quad f^{\prime }(\infty )\rightarrow S\,, \\ \theta (0)=1\,, \quad \theta (\infty )\rightarrow 0\,, $

where $S$ represents ratio of rates, $Q$ denotes the modified Hartmann number, $B$ denotes the non-dimensional parameter, $Pr $ shows Prandtl number, $\gamma $ depicts thermal relaxation parameter and $Ec$ denotes Eckert number. In mathematical form these parameters are:

$$ S =\frac{b}{a}\,, \quad Q=\frac{\pi j_{0}M_{0}}{8\rho a^{2}}\,,\quad B=\frac{\pi }{a_{1}}\sqrt{\frac{\upsilon }{a}}\,, Pr =\frac{\mu C_{p}}{k}\,, \quad Ec=\frac{U_{w}^{2}}{C_{p}( T_{w}-T_{\infty }) } \,,\quad \gamma =a\delta _{ E}\,, (14) $$

coefficients of skin friction i.e., $C_{f_{x}}$ is

(15)$ C_{f_{x}}=\frac{{ \tau }_{yx}}{\rho U_{w}^{2}}\,. $

The wall shear stress is given by

(16)$ { \tau }_{yx}=\mu \Big( \frac{\partial u}{\partial y}\Big) _{y=0}\,. $

In dimensionless variables one has

(17)$ C_{f_{x}}{Re}_{x}^{1/2}=f^{\prime \prime }(0)\,, $

where ${Re}_{x}={U_{w}x}/{\upsilon }$ depicts the local Reynolds number.

3 Homotopic Technique

Homotopic technique is developed in 1992 by Liao,^[23] which is helpful for the solution construction of highly nonlinear systems. Homotopy is a continuous variation or deformation of an equation or function. It has some advantanges in comparison to other methods i.e., (i) it does not depend on any large or small values selection of emerging parameters (ii) ensure the convergence of series solution (iii) free selection of linear operator and base function. For the computation of homotopic solutions, it is essential to define initial guesses and linear operators which are

(18)$ f_{0}( \eta ) =S\eta +( 1-S) (1-\exp (-\eta ))\,, \ \ \theta _{0}( \eta ) =\exp (-\eta )\,, $

(19)$ \mathcal{L}_{f}( f) =\frac{d^{3}f}{d\eta ^{3}}-\frac{d f}{d\eta }\,, \quad \mathcal{L}_{\theta }( \theta ) =\frac{d^{2}\theta }{d\eta ^{2}}\% -\theta \,, $

with the properties

(20)$ \mathcal{L}f[ B_{1}\exp (-\eta )+B_{2}\exp (\eta )+B_{3}] =0\,, $

(21)$ \mathcal{L}_{\theta }[ B4\exp (-\eta )+B5\exp (\eta )] =0\,. $

It should be noted that $B_{i}$ $( i=1,2,3,\ldots,5) $ represents arbitrary constants.

3.1 Zeroth-Order Problems

$$ ( 1-q) \mathcal{L}f[ \tilde{f}( \eta ;q) -f_{0}( \eta ) ] =q\hbar f\mathcal{N}_{f}[ \tilde{f }( \eta ;q) ,\tilde{\theta }( \eta ;q) ] \,, (22) $$

$$ ( 1-q) \mathcal{L}_{\theta }[ \tilde{\theta }( \eta ;q) -\theta _{0}( \eta ) ] =q\hbar _{\theta }\mathcal{\% N}_{\theta }[ \tilde{f}( \eta ;q) ,\tilde{\theta }\% ( \eta ;q) ] \,, (23) $$

$$ \tilde{f}( 0;q) =0\, \quad \tilde{f}^{\prime }( 0;q) =1\,, \quad \tilde{f}^{\prime }( \infty ;q) =S\,, (24) $$

$$ \tilde{\theta }( 0;q) =1\,,\quad \tilde{\theta }\% ( \infty ;q) =0\,, (25) $$

(26)$ \mathcal{N}_{f}[ \tilde{f}( \eta ,q) ] = \frac{\% \partial ^{3}\tilde{f}( \eta ;q) }{\partial \eta ^{3}}+\% \tilde{f}( \eta ;q) \frac{\partial ^{2}\tilde{f}( \eta ;q) }{\partial \eta ^{2}}-\Big( \frac{\partial \tilde{f}\% ( \eta ;q) }{\partial \eta }\Big) ^{2} +S^{2}+Q\exp ( -B\eta ) \,, $

(27)$ \mathcal{N}_{\theta }[ \tilde{\theta }( \eta ;q) ] = \frac{\partial ^{2}\tilde{\theta }( \eta ;q) }{\partial \eta ^{2}}+Pr \tilde{f}( \eta ;q) \frac{\partial \tilde{\% \theta }(\eta ,q)}{\partial \eta }+Pr Ec\Big( \frac{\partial ^{2}\% \tilde{f}( \eta ;q) }{\partial \eta ^{2}}\Big) ^{2} -Pr \gamma \Big( \tilde{f}( \eta ;q) \frac{\partial \tilde{f}( \eta ;q) }{\partial \eta }\frac{\partial \tilde{\theta }(\eta ,q)}{\partial \eta }+( \tilde{f}( \eta ;q) ) ^{2}\Big) +2Pr \gamma Ec\Big( \frac{\partial \tilde{f}( \eta ;q) }{\% \partial \eta }\Big( \frac{\partial ^{2}\tilde{f}( \eta ;q) }{\partial \eta ^{2}}\Big) ^{2}-\tilde{f}( \eta ;q) \frac{\% \partial ^{2}\tilde{f}( \eta ;q) }{\partial \eta ^{2}}\frac{\% \partial 3\tilde{f}( \eta ;q) }{\partial \eta ^{3}}\Big)\, . $

$q$ represents embedded parameter and varies from zero to one and non-zero auxiliary parameters are $\hbar _{f}$ and $h_{\theta }$

3.2 $k$-th Order Deformation Problems

(28)$ \mathcal{L}_{f}[ f_{k}( \eta ) -\chi _{k}\% f_{k-1}( \eta ) ] =\hbar _{f}\mathcal{R}_{k}^{f}( \eta ) \,, $

(29)$ \mathcal{L}\theta [ \theta _{k}( \eta ) -\chi _{k\% }\theta _{k-1}( \eta ) ] =\hbar _{\theta }\mathcal{R}\% _{k}^{\theta }( \eta ) \,, $

(30)$ f_{k}( 0) =0\,,\quad f_{k}^{\prime }( 0) =0\,, \quad \ f_{k}^{\prime }( \infty ) =0\,, $

(31)$ \theta _{k}( 0) =0\,,\quad \theta _{k}( \infty ) =0\,. $

For $k$-th order:

(32)$ \mathcal{R}_{k}^{f}( \eta ) =f_{k-1}^{\prime \prime \prime }+\sum_{p=0}^{k-1}( f_{k-1-p}f_{p}^{\prime \prime }) -\sum_{p=0}^{k-1}( f_{k-1-p}^{\prime }f_{p}^{\% \prime }) +S^{2}( 1-\chi _{k}) +Q\exp ( -B\eta ) \,, $

(33)$ \mathcal{R}_{k}^{\theta }( \eta ) =\theta _{k-1}^{\prime \prime } +Pr \sum_{p=0}^{k-1}( f_{k-1-p}\theta _{p}^{\prime }) +Pr Ec\sum_{p=0}^{k-1}( f_{k-1-p}^{\prime \prime }f_{p}^{\% \prime \prime }) -Pr \gamma \Big( \sum_{p=0}^{k-1}f_{k-1-p}\sum_{m=0}^{p}( f_{p-m}^{\% \prime }\theta _{m}^{\prime }) +\sum_{p=0}^{k-1}f_{k-1-p}\sum_{m=0}^{p}( f_{p-m}^{}\theta _{m}^{\prime \prime }) \Big) +2Pr \gamma Ec\Big( \sum_{p=0}^{k-1}f_{k-1-p}^{\prime }\sum_{m=0}^{p}( f_{p-m}^{\prime \prime }f_{m}^{\% \prime \prime }) +\sum_{p=0}^{k-1}f_{k-1-p}\sum_{m=0}^{p}( f_{p-m}^{\prime \prime }f_{m}^{\prime \prime \prime }) \Big) \,. $

Obviously for $q=0$ and $q=1$, one may write%

$$ \tilde{f}( \eta ;0) =f_{0}( \eta ) \,, \quad \tilde{f}( \eta ;1) =f( \eta ) \,, \tilde{\theta }( \eta ;0) =\theta _{0}( \eta ) \,, \quad \tilde{\theta }( \eta ;1) =\theta ( \eta )\, , $$

and with variation of $q$ from $0$ to $1$, $\tilde{f}( \eta ;q) $ and $\tilde{\theta }( \eta ;q) $ vary from the initial solutions $f_{0}( \eta ) $ and $\theta _{0}(\eta )$ to the final solutions $f( \eta ) $ and $\theta (\eta )$ respectively. Using Taylor series for $q=1$, we have

(34)$ f( \eta ) =f_{0}( \eta ) +\sum_{k=1}^{\infty }f_{k}( \eta ) \,, $

(35)$ \theta ( \eta ) =\theta _{0}( \eta ) +\sum_{k=1}^{\infty }\theta _{k}( \eta ) \,. $

The general solutions $( f_{k} \text{ and }\theta _{k}) $ of Eqs. (29)--(32) corresponding to special solutions $( f_{k}^{\% \ast }\text{ and }\theta _{k}^{\ast }) $ are

(36)$ f_{k}( \eta ) =f_{k}^{\star }( \eta ) +B_{1}e^{-\eta }+B_{2}e^{\eta }+B_{3}\,, $

(37)$ \theta _{k}( \eta ) =\theta _{k}^{\star }( \eta ) +B_{4}e^{-\eta }+B_{5}e^{\eta }\,, $

where the constants $B_{i}$ $(i=1,2,\ldots,5)$ are computed through the boundary conditions (33). We ultimate have

(38)$ B_{2} =0\,,\quad B_{1}=-\frac{\partial f_{k}^{\star }( \eta ) }{\partial \eta }\Bigm| _{\eta =0}\,, \\ B_3=-f_{k}^{\star }( 0) - \frac{\partial f_{k}^{\% \star }( \eta ) }{\partial \eta }\Bigm| _{\eta =0}\,, \\ B_{5} =0\,, \quad B_{4}=-\theta _{k}^{\star }( 0)\,. $

4 Convergence of the Series Solutions

Homotopic technique provides and guarantees the convergent series solutions in an easy way. To ensure the convergence graphical behavior of solutions are constructed corresponding to auxiliary parameters (see Fig. 2). This figure witnesses that the acceptable convergence regions are $-1.7\leq \hbar _{f}\leq -0.3$ and $-1.8\leq \hbar _{\theta }\leq -0.4$.

Fig. 2

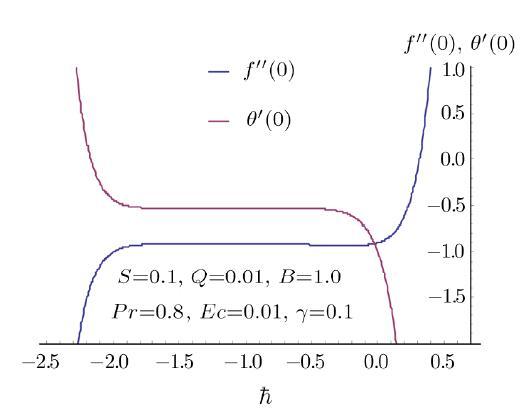New window|Download| PPT slide
Fig. 2$h$-curves for $f(\eta )$ and $\theta (\eta )$.

5 Disscusion

This section reports that how representative physical parameters affect various quantities of interest such as velocity and temperature distributions. For this purpose, Figs. 3--9 are displayed. Figure 3 depicts the velocity field, $f^{\prime }(\eta )$ is sketched against ration parameter $S$. It is identified that velocity field rises with increasing ration parameter $S$. Its boundary layer thickness gets steeper with increasing $S$. Physically increasing values of ration parameter $S$ induces a supporting free stream velocity, which helps enhancing the velocity distribution.

Fig. 3

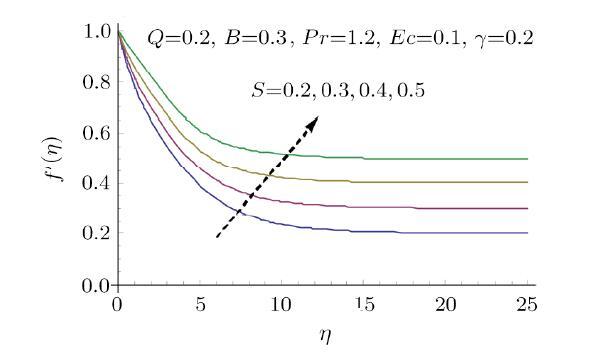New window|Download| PPT slide
Fig. 3Effect of $S$ on $f^{\prime }$.



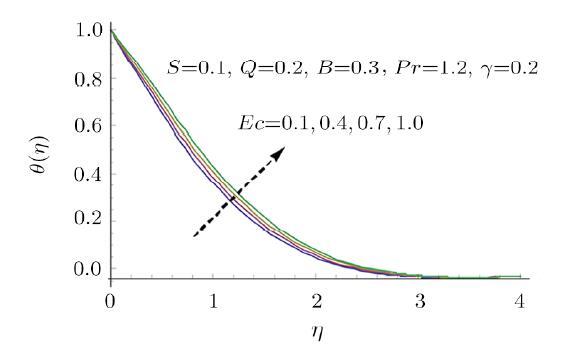
Figure 4 illustrates the velocity distribution corresponding to modified Hartmann number $Q$. Higher intensity of modified Hartmann number $Q $ give rise to velocity distribution. Physically modified Hartman number $Q $ is dominating and thus it assists the flow due to more intensity of external electric field and as a consequence the wall parallel lorentz force produces. Hence the velocity field exceeds. Moreover the thicker velocity boundary layer is observed corresponding to growing $Q$. Figure 5 demonstrates how the Prandtl number $Pr$ affects the temperature distribution. An expecting observation is made from this figure i.e. temperature decays with increasing Prandtl number $Pr$. For larger Prandtl number $Pr$ the momentum diffusivity effects dominate the effect of thermal diffusivity, which shifts the low transfer of heat from heated surface towards the cold ambient fluid. As a consequence the temperature reduces. Figure 5 further shows that thermal boundary layer becomes thinner with growing $Pr$. Figure 6 is plotted to see the behavior of temperature distribution against dimensionless Eckert number $Ec$. This figure illustrates the increasing trend of temperature field for dominating effects of Eckert number $Ec$. The variation in fluid temperature is confined to a thick boundary layer. %This makes evident the existance of thick thermal boundary %layer for larger Eckert number $Ec$. However due to dominating Eckert number $Ec$ more heat generation in fluid occurs because of strong friction force between the fluid particles. Therefore fluid temperature rises.

Fig. 4

New window|Download| PPT slide
Fig. 4Effect of $Q$ on $f^{\prime }$.

Fig. 5

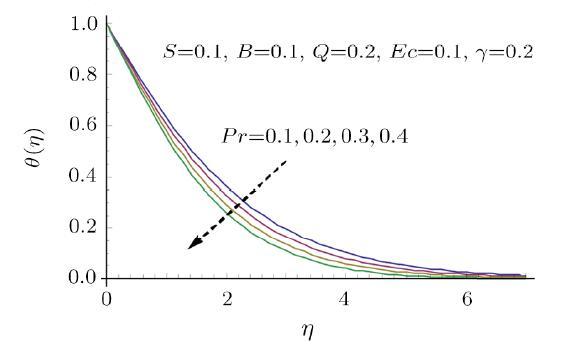New window|Download| PPT slide
Fig. 5Effect of $Pr $ on $\theta $.

Fig. 6

New window|Download| PPT slide
Fig. 6Effect of $Ec$ on $\theta $.



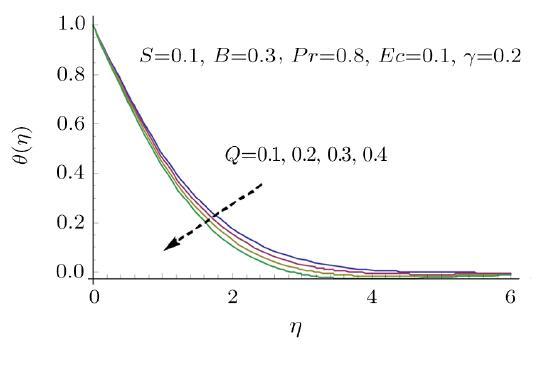
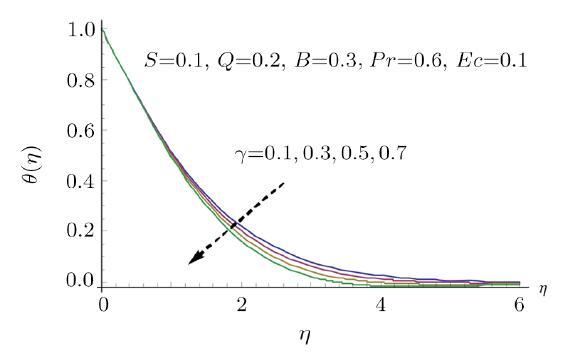
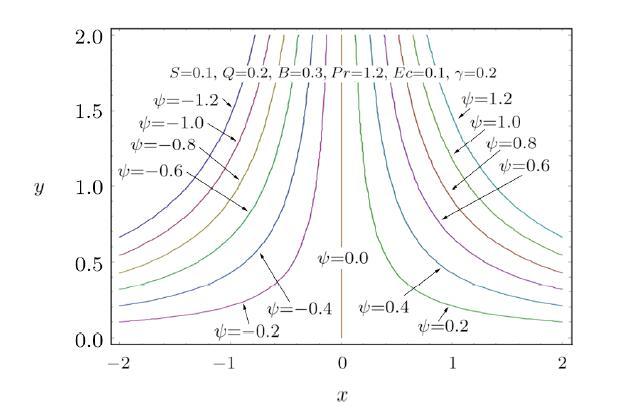
Figure 7 shows how the modified Hartman number $Q$ affects the temperature distribution. The temperature decreases with increasing modified Hartman number $Q$. The thick thermal boundary layer can be seen for larger $Q$. The temperature exceeds at the surface of the sheet due to the assistance provided by the wall parallel Lorentz force to the flow induced by stretchable Riga plate. However it gradually decreases away from the surface. Hence the temperature distribution decays. Figure 8 plots the temperature distribution versus thermal time relaxation parameter $\gamma $. The fluid's temperature and the thickness of associated boundary layer decreases with increasing $\gamma $. In fact for larger thermal time relaxation parameter $\gamma $ the fluid particles take additional time for transporting heat to the adjacent particles, which illustrates decrement in temperature field. Fourier model deduces by setting $\gamma =0$. In this case the heat is transferred through out the material with infinite speed and thus temperature distribution raises for $\gamma =0$. Figure 9 discloses the effects of ration parameter $S$ and modified Hartman number $Q$ on skin friction coefficient $Cf$. The skin friction coefficient $Cf$ decreases with increasing ration parameter $S$ and modified Hartman number $Q$. Figure 10 reflects the behavior of streamlines for the present flow.

Fig. 7

New window|Download| PPT slide
Fig. 7Effect of $Q$ on $\theta $.

Fig. 8

New window|Download| PPT slide
Fig. 8Effect of $\gamma $ on $\theta $.

Fig. 9

New window|Download| PPT slide
Fig. 9Effec of $S$ and $Q$ on $Cf$.

Fig. 10

New window|Download| PPT slide
Fig. 10Streamlines for the flow.

6 Conclusions

We present the mathematical analysis to explore the heat transfer effects via Cattaneo-Christov heat flux model with viscous dissipation on staganation point flow past a stretchable Riga plate. We obtained the exact expression for velocity and temperature field which is computed analytically. Graphs display how the involved parameters affect the abovementioned distributions. The concluding points in the whole study are listed below:

(i) The flow velocity increases and boundary layer associated with velocity become thick by dominating modified Hartman number $Q$ and ratio parameter $S$.

(ii) Eckert number $Ec$ increases the temperature distribution.

(iii) An increase in modified Hartman number $Q$ leads to decay the fluid's temperature.

(iv) Temperature decreases with increasing thermal relaxation parameter $% \gamma $.

(vi) Skin frictio/drag force can be increased by enhancing $S$ and $Q$.

The authors have declared that no competing interests exist.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] P. Weidman and M. R. Turner , Eur. J. Mech.-B/Fluids 61 (2017) 144.
DOI:10.1016/j.euromechflu.2016.09.019URL [Cited within: 1]
A unified formulation for stagnation-point flows and linearly stretching plates is given wherein the two can occur separately or in unison. Reductions to known cases are given. It is noticed that previous work on stretching plates beneath planar and axisymmetric stagnation point flows have respectively aligned planar stretching and axisymmetric stretching. The general formulation reveals other combinations of stretching beneath stagnation-point flows exist and three new cases are studied in detail. The linear stability of dual and multiple solutions are calculated.

[2] J. H. Merkin , N. Najib, it et al., N Bachok, and A. Ishak, Pop, I. J. Taiwan Inst. Chem. Eng. 74(2017) 65.
DOI:10.1016/j.jtice.2017.02.008URL [Cited within: 1]
The stagnation-point boundary-layer flow and heat transfer over an exponentially stretching/shrinking cylinder is studied. The governing partial differential equations in cylindrical form are first transformed into ordinary differential equations which are then solved numerically using a shooting method. Results for the skin friction coefficient, local Nusselt number, velocity and temperature profiles are presented and discussed in detail. The effects of the stretching/shrinking parameter 系 and the curvature parameter纬on the fluid flow and heat transfer characteristics are also examined. It is found that the solutions for a shrinking cylinder are non-unique and that the surface shear stress and the heat transfer rate at the surface increase as the curvature parameter increases.

[3] A. Borrelli, G. Giantesio, M. C . Patria, et al., Commun.Nonlinear Sci. Numer. Simul. 43(2017) 1.
DOI:10.1016/j.cnsns.2016.06.022URL [Cited within: 1]
This work examines the steady three-dimensional stagnation-point flow of an electrically conducting Newtonian fluid in the presence of a uniform external magnetic fieldH0under the Oberbeck–Boussinesq approximation. We neglect the induced magnetic field and examine the three possible directions ofH0which coincide with the directions of the axes. In all cases it is shown that the governing nonlinear partial differential equations admit similarity solutions. We find that the flow has to satisfy an ordinary differential problem whose solution depends on the Hartmann numberM, the buoyancy parameterλand the Prandtl numberPr. The skin-friction components along the axes are computed and the stagnation-point is classified. The numerical integration shows the existence of dual solutions and the occurrence of the reverse flow for some values of the parameters.

[4] T. M. Agbaje, S. Mondal, Z. G . Makukula, et al., Ain Shams Eng.J. 9(2018) 233.
DOI:10.1016/j.asej.2015.10.015URL [Cited within: 1]
Magnetohydrodynamic (MHD) stagnation point flow and heat transfer problem from a stretching sheet in the presence of a heat source/sink and suction/injection in porous media is studied in this paper. The governing partial differential equations are solved using the Chebyshev spectral method based perturbation approach. The method, namely the spectral perturbation method (SPM), is a series expansion technique which extends the use of the standard perturbation approach by coupling it with the Chebyshev pseudo-spectral method. Series solutions for small velocity ratio and asymptotic solutions for large velocity ratio are generated and the results are also validated against those obtained using the spectral quasi-linearisation method (SQLM). It is seen from this study that the SPM can be used as an alternative approach to find numerical solutions for complicated expansions encountered in perturbation schemes. The results are benchmarked with previously published results.

[5] P. R. Sharma, S. Sinha, R. S. Yadav, A. N. Filippov , Int. J. Heat Mass Trans. 117(2018) 780.
DOI:10.1016/j.ijheatmasstransfer.2017.10.026URL [Cited within: 1]
Aim of the paper is to investigate the effects of heat generation/absorption on MHD mixed convective stagnation point flow along a vertical stretching sheet in the presence of external magnetic field. The governing boundary layer equations are formulated and transformed into nonlinear ordinary coupled differential equations using similarity transformation and numerical solution is obtained by using Runge-Kutta fourth order scheme with shooting technique. The effects of various physical parameters such as velocity ratio parameter, mixed convection parameter, Hartmann number, Prandtl number and heat source/sink on velocity and temperature distributions are presented through graphs and discussed numerically. The skin friction coefficientand Nusselt number at the sheet are derived, discussed numerically and their numerical values are presented through tables.

[6] M. M. Bhatti, M. A. Abbas, M. M. Rashidi , Appl. Math. Comput. 316(2018) 381.
[Cited within: 1]

[7] C. Cattaneo , Atti Semin. Mat Fis Univ Modena Reggio Emilia 3 (1948) 83.
[Cited within: 1]

[8] C. I. Christov , Mech. Res. Commun. 36( 4) ( 2009) 481.
DOI:10.1016/j.mechrescom.2008.11.003URL [Cited within: 1]
A material-invariant (frame indifferent) version of the Maxwell–Cattaneo law is proposed in which the relaxation rate of the heat flux is given by Oldroyd’s upper-convected derivative. It is shown that the new formulation allows for the elimination of the heat flux, thus yielding a single equation for the temperature field. This feature is to be expected from a truly frame indifferent description.

[9] T. Hayat, M. I. Khan , M. Farooq, et al., J. Molec. Liq. 220(2016) 49.
DOI:10.1016/j.molliq.2016.04.032URL [Cited within: 1]
61Stagnation point flow of Maxwell fluid is investigated over a stretching cylinder.61Cattaneo-Christov heat flux model is incorporated instead of Fourier's law of heat conduction.61Characteristics of heat transfer are explored in the presence of homogeneous-heterogeneous reaction.61Time dependent variable thermal conductivity is also utilized.

[10] T. Hayat, M. T. Khan , M. Farooq, et al., Int. J. Heat Mass Trans. 106(2017) 289.
DOI:10.1016/j.ijheatmasstransfer.2016.10.071URL [Cited within: 1]
The present article addresses the stagnation point flow of Jeffrey liquid towards a stretching cylinder. Heat transfer is analyzed in view of non-Fourier heat flux and thermal stratification. Expression of heat flux is based upon Cattaneo–Christov theory. Cattaneo–Christov heat flux model is utilized for the development of energy equation. Such consideration accounts the contribution by thermal relaxation. The series solutions for resulting flow and heat transfer problems have been computed. Interval of convergence for the obtained series solutions is explicitly determined. Physical quantities of interest have been examined for the influential variables entering into the problems. It is observed that velocity profile shows decreasing behavior for larger Deborah number. Further that temperature distribution decreases for larger values of thermally stratification and thermal relaxation parameters.

[11] M. Zubair, M. Waqas , T. Hayat, et al., Res. Phys. 8(2018) 1023.
[Cited within: 1]

[12] M. I. Khan, T. Hayat, M. I. Khan, A. Alsaedi , Int. J. Heat Mass Trans. 113(2017) 310.
DOI:10.1016/j.ijheatmasstransfer.2017.05.082URL [Cited within: 1]

[13] A. Hussain, M. Y. Malik , T. Salahuddin, et al., J. Mol. Liq. 231(2017) 341.
DOI:10.1016/j.molliq.2017.02.030URL [Cited within: 1]
61MHD Sisko nanofluid is analyzed over stretching cylinder.61Combined effects of viscous dissipation and Joule heating are discussed.61Numerical solution is computed via shooting technique.61Accuracy has been proved by comparing results with reported data.

[14] M. Waqas, M. I. Khan, T. Hayat, A. Alsaedi , Commun. Theor. Phys. 70(2018) 025.
DOI:10.1088/0253-6102/70/1/25URL [Cited within: 1]
Here thermal dependence conductivity and nonlinear convection features in third-grade liquid flow bounded by moving surface having varying thickness are formulated. Stagnation point flow is considered. Revised FourierFick relations and double stratification phenomena are utilized for modeling energy and concentration expressions.Mathematical model of considered physical problem is achieved by implementing the idea of boundary layer theory. The acquired partial differential system is transformed into ordinary ones by employing relevant variables. The homotopic scheme yield convergent solutions of governing nonlinear expressions. Graphs are constructed for distinct values of physical constraints to elaborate the heat/mass transportation mechanisms.

[15] A. Ahmad, S. Asghar, S. Afzal, J. Magn. Magn Mater. 402(2016) 44.
DOI:10.1016/j.jmmm.2015.11.043URL [Cited within: 1]
61Mixed convection flow of a nanofluid past a vertical Riga plate.61The Brownian motion and thermophoresis effects due to nanofluid are incorporated.61Grinberg-term represents the wall parallel Lorentz force due to Riga plate.61The correlation expressions for skin friction, Nusselt and Sherwood numbers are developed.61The effects of nanofluid and the Lorentz force on the skin friction are discussed.

[16] T. Hayat, T. Abbas , M. Ayub, et al., J. Mol. Liq. 222(2016) 854.
DOI:10.1016/j.molliq.2016.07.111URL [Cited within: 1]

[17] M. Farooq, A. Anjum, T. Hayat, A. Alsaedi, J. Mol. Liq. 224(2016) 1341.
DOI:10.1016/j.molliq.2016.10.123URL [Cited within: 1]
61Mathematical model is developed for stagnation point flow of viscous fluid over a nonlinear stretched surface.61Deformation in the fluid is produced by Riga plate of variable thickness.61Characteristics of melting heat transfer are explored with viscous dissipation.61Homogeneous-heterogeneous reactions are also tackled.

[18] T. Hayat, M. Khan, M. Imtiaz, A. Alsaedi, J. Mol. Liq. 225(2017) 569.
DOI:10.1016/j.molliq.2016.11.089URL [Cited within: 1]

[19] R. Ahmad, M. Mustafa, M. Turkyilmazoglu , Int. J. Heat Mass Trans. 111(2017) 827.
DOI:10.1016/j.ijheatmasstransfer.2017.04.046URL [Cited within: 1]

[20] A. Naseem, A. Shafiq, L. Zhao, M. U. Farooq , Res. Phys. 9(2018) 961.
[Cited within: 1]

[21] S. Shah, S. Hussain, M. Sagheer , Res. Phys. 9(2018) 303.
[Cited within: 1]

[22] I. H. Qureshi, M. Nawaz, S. Rana, T. Zubair , Commun. Theor. Phys. 70(2018) 049.
DOI:10.1088/0253-6102/70/1/49URL [Cited within: 1]
This article investigates the effects of variable thermal conductivity and variable mass diffusion coefficient on the transport of heat and mass in the flow of Casson fluid. Numerical simulations for two-dimensional flow induced by stretching surface are performed by using Galerkin finite element method(GFEM) with linear shape functions. After assembly process, nonlinear algebraic equations are linearized through Picard method and resulting linear system is solved iteratively using Gauss Seidal method with simulation tolerance 10~(-8). Maximum value of independent variable畏 is searched through numerical experiments. Grid independent study was carried out and error analysis is performed.Simulated results are validated by comparing with already published results. Parametric study is carried out to explore the physics of the flow. The concentration increases when mass diffusion coefficient is increased. The concentration and thermal boundary layer thicknesses increase when ?_1 and ? are increased. The effect of generative chemical reaction on concentration is opposite to the effect of destructive chemical reaction on the concentration.

[23] S. J. Liao , Homotopy Analysis Method in Non-Linear Differential Equations, Springer and Higher Education Press, Heidelberg( 2012).
[Cited within: 2]

[24] S. J. Liao, Advances in the Homotopy Analysis Method, World Scientific, Singapore (2014).


[25] T. Hayat, S. Ali, M. Awais, M. S. Alhuthali , Appl. Math. Mech. 36(2015) 61.
DOI:10.1007/s10483-015-1895-9URL
The Newtonian heating effects in the stagnation point flow of a Burgers fluid are addressed in this paper. The boundary layer flow problems are stated in the spatial domain from zero to infinity. The solution expressions for the velocity and the temperature are obtained and examined for the influential variables. The tabulated values show comparison with the previous results. It is observed that the obtained results are in good agreement with the existing results in limiting sense.

[26] T. Hayat, S. Ali, M. A. Farooq, A. Alsaedi , PLOS ONE 10 ( 9) ( 2015) e0129613.
DOI:10.1371/journal.pone.0129613URLPMID:26402366
In this paper, we have investigated the combined effects of Newtonian heating and internal heat generation/absorption in the two-dimensional flow of Eyring-Powell fluid over a stretching surface. The governing non-linear analysis of partial differential equations is reduced into the ordinary differential equations using similarity transformations. The resulting problems are computed for both series and numerical solutions. Series solution is constructed using homotopy analysis method (HAM) whereas numerical solution is presented by two different techniques namely shooting method and bvp4c. A comparison of homotopy solution with numerical solution is also tabulated. Both solutions are found in an excellent agreement. Dimensionless velocity and temperature profiles are plotted and discussed for various emerging physical parameters.

[27] T. Hayat, M. I. Khan, S. Qayyum, A. Alsaedi , Colloids and Surfaces A: Phys. Eng.Aspec. 539(2018) 335.
DOI:10.1016/j.colsurfa.2017.12.021URL
The purpose of this attempt is mainly to explore the mixed convective flow of viscous fluid by a rotating disk. Thermal radiation, Joule heating, variable thickness and viscous dissipation have been accounted. Flow under consideration is because of nonlinear stretching characteristics of disk. Water is treated as traditional fluid while nanoparticles include silver and copper. Fluid is electrically conducting subject to applied magnetic field with constant strength. Heat generation and absorption is neglected. An entropy generation analysis is utilized through second law of thermodynamics. The effects of silver and copper nanoparticles on the thermal conductivity of continuous phase fluid and entropy generation have been also examined. Total entropy generation rate is scrutinized for different involved variables. Nonlinear formulation based upon conservation laws of mass, momentum and energy is made. Attention is particularly given to the convergence in the computational process. Velocity and thermal gradients at the surface of disk are obtained in tabular forms. Main conclusions have been indicated.

[28] M. I. Khan, T. Hayat, M. I. Khan, A. Alsaedi , Int. Commun. Heat Mass Trans. 91(2018) 216.
DOI:10.1016/j.icheatmasstransfer.2017.11.001URL
Here modeling and computations are presented to introduce the novel concept of activation energy in mixed convective magnetohydrodynamic (MHD) stagnation point flow towards a stretching surface. Chemical reaction at the surface is implemented. Nanofluid aspects for thermophoresis and Brownian motion have been considered. Nonlinear thermal radiation and heat absorption/generation are presented. Nonlinear computations have been presented using Runge–Kutta–Fehlberg (RKF) Numerical Method. Main focus in this study for the description of velocity, temperature and nanoparticle concentration. Skin friction coefficient, Nusselt and Sherwood numbers are computed and discussed in Tables. Our investigations reveal that species concentration enhances for higher estimation of activation energy variable. Nusselt and Sherwood numbers show similar behavior for rising values of Weissenberg number.

[29] N. Muhammad, S. Nadeem, M. T. Mustafa , PLOS ONE 13 (2018) e0188160.


[30] S. Nadeem, S. Ahmad, N. Muhammad, M. T. Mustafa , Res. Phys. 7(2017) 2607.
[Cited within: 1]