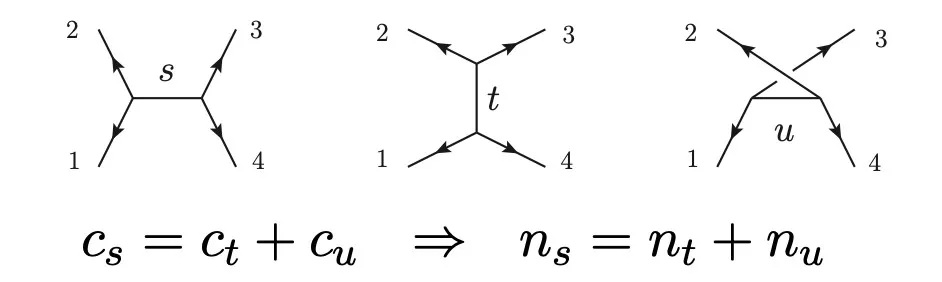
图1:四胶子振幅可以用s、t、u三个图表示,其动量因子n满足和色因子c相同的代数关系。
色-动量对偶关系暗示着规范和时空两种对称性存在紧密的联系。在规范理论中,物理量满足规范对称性和时空对称性;而在引力理论中,物理量满足的对称性只有时空对称性。读者可能会问,既然规范对称性和时空对称性存在紧密的联系,那么规范理论和引力理论中的物理量是否也有紧密的关系?事实上,借助色-动量对偶,可以从“满足对偶的”规范振幅来直接构造引力振幅 [2]:只需要把色因子进一步替换为动量因子,这样得到的包含动量因子平方的振幅就是引力振幅。图2表示了四胶子和四引力子振幅的例子。这一神奇的联系英文一般称为“double copy”,我们这里暂且称为“平方关系”,取“引力 = 规范场的平方”的意思 [3]。
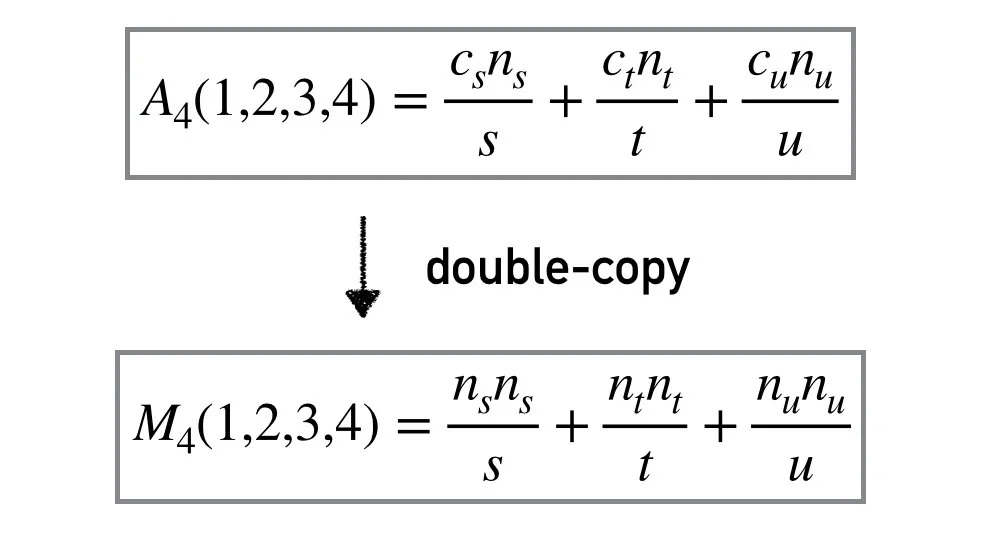
图2:四胶子振幅的动量因子平方可以直接给出四引力子振幅。
借助平方关系构造引力的一个前提条件是,规范振幅必须满足色-动量对偶。那是否一定能构造这样的规范振幅呢?很遗憾,目前除了对于树图振幅有证明外,对于包含量子修正的一般圈图情形还只是一个猜想,其成立性没有任何一般性证明。虽然人们已经发现了很多圈图的例子,但随着圈数和外线数的增加,找到这样的例子就变得非常具有挑战性了。比如最大超对称场论中的四胶子振幅,至今也没有实现其五圈的对偶。如果能证明色-动量对偶在一般量子水平存在,借助平方关系将无疑会对理解量子引力提供极大的促进,甚至有可能最终解决量子引力问题。
最近,理论物理所的杨刚研究员和北京大学本科生林冠达、理论物理所研究生张思源在研究色-动量对偶方面取得新进展,首次发现了一类三圈形状因子的满足对偶关系的解;特别的,他们发现这个解空间还意外的大,比如对于能动量守恒流算符的情形,其解空间包含多达24个自由参数。这一成果发表于Physical Review Letters (Vol. 127, No. 17, 2021) [4]。
在这一课题中,作者考虑了一类超对称场论中的三圈三点形状因子,这类物理量可以类比于Higgs到三个胶子过程的散射振幅。两圈水平的研究表明这些超对称形状因子可以给出QCD结果中函数最复杂的最大超越函数部分 [5],所以和唯象学也有紧密的联系。以上述能动量守恒流算符相关的形状因子为例,图3表示了该形状因子的示意图以及所涉及的29个费曼图。
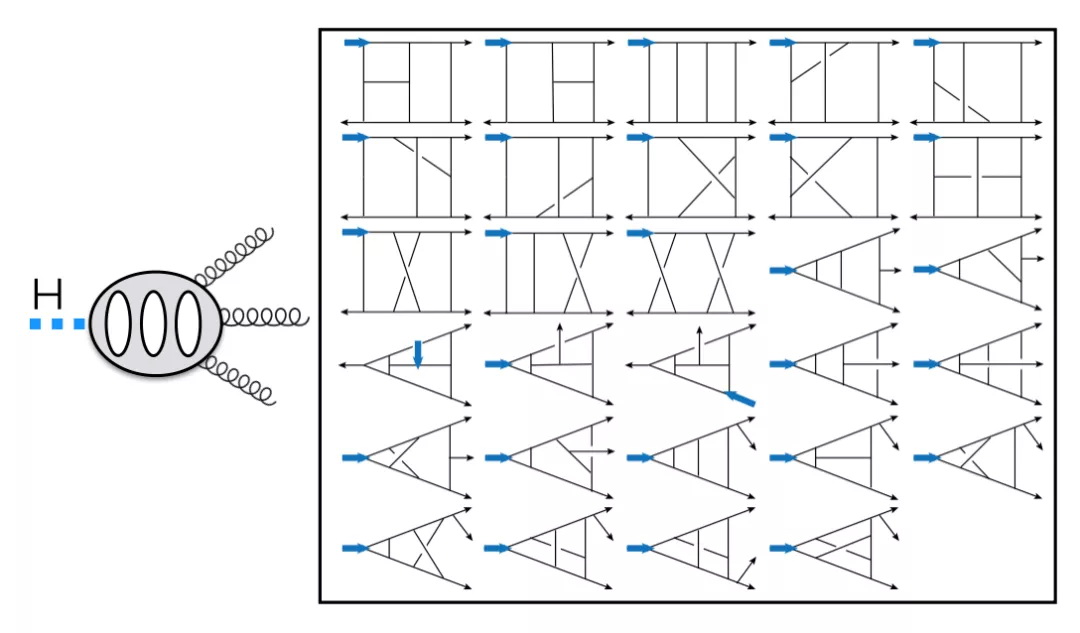
图3:三圈的费曼图。
这些新结果的一个重要特征是带有色-动量对偶结构,正如前文所言,这一结构隐藏着深刻的物理意义。在规范理论的振幅中,选取不同的“规范”,可能会给出看起来差别很大的不同形式,进而从不同的侧面反映出振幅的性质。色-动量对偶的结构指的是:存在一类特殊的“规范”选择,使得振幅或形状因子表现出色-动量对偶这一特别的性质,此时色因子和动量因子会满足一一对应的关系。杨刚等人最新的三圈结果,不仅给出了圈图水平上色-动量对偶的新的证据,而且表明即使是上述特殊的“规范”选择也还可能有很大的解空间。这些带有新特征的解可以成为帮助更好理解色-动量对偶的有用素材,进而也会有助于更好地理解上述平方关系甚至量子引力问题。
此外,课题组还对所得结果实现了非常具有挑战性的三圈积分的计算,并进一步研究了其他一些有趣的性质。比如其中很重要一点是,三圈的物理量首次表现出非平面的非偶极红外结构。文章也对这类性质做了仔细研究。
参考文献:
[1] Z. Bern, J. Carrasco, and H. Johansson, “New Relations for Gauge-Theory Amplitudes”, Phys. Rev. D78 (2008) 085011.
[2] Z. Bern, J. Carrasco, and H. Johansson, “Perturbative Quantum Gravity as a Double Copy of Gauge Theory”, Phys.Rev.Lett. 105 (2010) 061602.
[3] 值得一提的是,在80年代Kawai, Lewellen, 和戴自海等人就发现弦理论中闭弦振幅可以写成开弦振幅的平方,见H. Kawai, D. Lewellen, H. Tye, “A Relation Between Tree Amplitudes of Closed and Open Strings”, Nucl.Phys.B 269 (1986) 1-23,给出了最早的平方关系的例子。但色-动量对偶提供了全新的图像,基于这一对偶的平方关系可以在圈图有非常自然的直接推广。
[4] G. Lin, G. Yang, S. Zhang, “Three-Loop Color-Kinematics Duality: A 24-Dimensional Solution Space Induced by New Generalized Gauge Transformations”, Phys. Rev. Lett. 127 (2021) 17.
[5] A. Brandhuber, G. Travaglini, G. Yang, “Analytic two-loop form factors in N=4 SYM”, JHEP 05 (2012) 082; T. Gehrmann, M. Jaquier, E. Glover, A. Koukoutsakis, “Two-Loop QCD Corrections to the Helicity Amplitudes for H to 3 partons”, JHEP 02 (2012) 056.
