在散射振幅以及更一般地对量子场论的研究中,人们往往倾向于首先在一个更简单但依然具有丰富结构的理论中发展新工具、发现新结构,然后将这些工具和结构应用到标准模型等实际理论中去。平面极限下的最大超对称规范场论(planar N=4 SYM)正是这样的一种理论。它具有某些标准模型所没有的,如共形对称性等更强的对称性,其包括散射振幅在内的物理量拥有更简单的结构,以及与引力、弦论和数学物理等方面的紧密联系。特别地,由于 planar N=4 SYM 理论拥有一种新的隐藏对称性,即对偶超共形对称性(dual conformal invariance,DCI),人们从对偶空间(动量构成的空间)的视角发掘了该理论令人意想不到的新结构。其中,对偶空间中的超对称Wilson圈与振幅的对偶尤其引人瞩目,在超对称Wilson圈的表述下,振幅的对偶超共形对称性变得完全显明,这不仅导致了正Grassmannian几何 [1] 等重要的数学发现,也提供了一系列振幅的新计算方法,例如基于Yangian对称性与可积性的Qbar方法 [2]。
与此同时,振幅的费曼图表示也是长盛不衰的一大方法,广泛应用于各种的理论的微扰计算中, 例如微扰论每一阶的振幅计算可以表达为一系列费曼图的求和,当然这些费曼图的计算往往非常复杂。由于 N=4 SYM 的振幅具有更强的对称性,一个自然的问题是, N=4 SYM 是否有更简单的费曼图表示,且单个费曼图的结果也具有一定的对称性?2010年,Nima Arkani-Hamed等人对于N=4 SYM 的圈图振幅发现了一种全新的费曼图展开,使得每一副费曼图的结果都具有诸如对偶共形对称性,有限性与局域性等良好的性质[3]。但是,由于这些积分是动力学参量的复杂代数函数,直接计算十分困难。尽管物理学家们对这些费曼图的积分结果的结构有了一定的预期,却始终没有得到过它们的具体结果。
近日,中国科学院理论物理所的何颂研究员,博士生李振杰,硕士生杨清霖与尼尔斯·玻尔研究所的博士后张驰在此方向取得了重要成果。他们基于一些费曼图也有Wilson圈解释这个观察[4],将许多难以计算的费曼图化为较简单的类似于Wilosn圈计算中线积分的形式。特别地,他们通过这个方法计算了图中被称为“双圈手征五边形图”的费曼积分,将两圈积分化为一圈积分的两重线积分的形式,并通过一些既有的算法首次给出了该积分结果的结构。
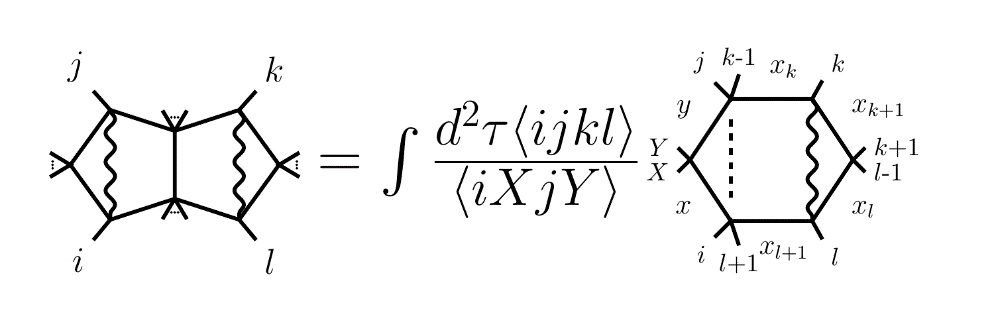
在计算的过程中,他们通过应用“有理化”的计算思想[5],完成了含有积分变量平方根的多对数函数的迭代积分,解决了积分结果本身是参量复杂代数函数这一难题。该积分的结果就可以给出planar N=4 SYM理论中当外腿为最大螺旋度破坏(MHV)情况下任意粒子数的两圈振幅。这一成果不仅为对偶共形不变的费曼积分的计算提供了重要的新结果,同时也可以应用于一类更一般的多腿对偶共形不变的高圈积分计算。这一方法对更一般的费曼积分和散射振幅的计算提供了启发,并引发了一系列关于费曼积分数学结构的新研究。

该研究成果近日发表在Phys.Rev.Lett. 126 (2021) 231601上。相关工作得到了中科院前沿重点研究项目,国家自然科学基金重点项目和“彭桓武理论物理创新研究中心”, ERC starting grant and grant from the Villum Fonden等资助。
参考文献
[1] N.Arkani-Hamed, J.Bourjaily, F.Cachazo, A. Goncharov, A. Postnikov, and J.Trnka, Grassmannian Geometry of Scattering Amplitudes, Cambridge University Press,2016.
[2]. S. Caron-Huot, S. He, Jumpstarting the All-Loop S-Matrix of Planar N=4 Super Yang-Mills, 10.1007/JHEP07(2012)174
[3] N.Arkani-Hamed, J.Bourjaily, F.Cachazo and J.Trnka, Local Integrals for Planar Scattering Amplitudes, 10.1007/JHEP06(2012)125.
[4] S.He, Z.Li, Y.Tang and Q.Yang, The Wilson-loop d log representation for Feynman integrals,10.1007/JHEP05(2021)052.
[5] S.He, Z.Li and C.Zhang, Two-loop octagons, algebraic letters and Qbar equations, 10.1103/PhysRevD.101.061701; The symbol and alphabet of two-loop NMHV amplitudes from Qbar equations, 10.1007/JHEP03(2021)278
