作为理论物理基本概念之一,自发对称性破缺已被研究得非常透彻了。对于由宏观数目的个体通过相互作用相互影响而构成的统计物理多体系统,自发对称性破缺是一种集体行为。它的微观机制粗略地说,就是当系统达到某种条件后(例如温度足够低),这些宏观数目的个体都“觉得”协同行动能“让自己更为舒适”,于是系统在宏观上就(无意识的)从一个较为无序的相演化到一个更为有序的相,伴随着对称性和自由度的显著降低。
珀兹(Potts)模型是研究统计物理系统自发对称性破缺的范例。在该简单模型中,系统的N个粒子处于一个相互作用网络中,每个粒子占据网络的一个节点不可移动,但它可选择Q种不同颜色之一(例如赤、橙、黄、绿、青、蓝、紫,Q=7)。网络中邻近(即有一条边相连)的粒子之间有相互影响,它们喜欢彼此颜色相同,如果颜色相同则相互作用势能低(等于0),如果颜色不同则相互作用势能高(等于1)。系统的总能量就是所有相邻粒子相互作用势能之和。显然,系统在高能量时可以处于许许多多不同的微观构型,导致每种颜色的比例平均而言都非常接近,因而系统总体呈现白色。当系统的总能量足够低以至接近于零时,对应的微观颜色构型就会变得很少,绝大多数粒子都会处于同一种颜色状态,因而系统整体呈现一种很鲜明的颜色(例如蓝色,但也可以是Q种颜色的任意其它颜色之一),导致颜色的对称性破缺。
以前对珀兹模型的研究集中于考虑系统性质随温度的变化(称为正则系综),发现当颜色数目Q比较大时,随着环境温度的降低,系统将在某个临界温度处发生颜色的爆炸式(或称为非连续)自发对称性破缺,即某一颜色的比例突然从 1/Q 跳跃至一个较大的值。这一相变行为伴随有系统能量密度的突然降低,即很大一部分系统的内部能量流到了环境中,以维持住系统的有序性。
如果我们不允许珀兹模型系统与环境发生能量的交换,而是使它处于绝热的孤立状态,只能在固定的总能量下演化,或者它的总能量最多只能非常缓慢地改变(称为微正则系综),在这种情况下发生的颜色自发对称性破缺还能是爆炸式的吗?以前的统计物理平均场理论认为,在内能固定的情况下爆炸式非连续自发对称性破缺不会发生,因为系统无法通过降低能量来换取状态的有序(即降低熵)。但是,最近中国科学院理论物理研究所周海军研究员通过理论计算发现,固定能量下的颜色自发对称性破缺可以是爆炸式的。
给定两个相同的系统,其中一个(A)的内能密度比某个临界值umic稍高一点点,而另一个(B)的内能密度比临界值umic稍低一点点,周海军发现这两个系统的状态可以有非常大的差别:系统A是纯白色的(各种颜色的比例相同),而系统B的颜色显著偏离白色(例如蓝色粒子的比例显著高于其它Q-1种颜色粒子的比例)。而且,处于对称性破缺后的有序态的系统B的温度比处于无序态的系统A要显著地更热一些!
周海军在随机网络和有限维稀疏晶格系统上获得的计算机模拟结果验证了这些奇异的自发对称性破缺理论预言,论文近期发表于:Physical Review Letters 122, 160601(2019)。这些现象背后的理论原因是系统的熵(它描述微观状态数的多寡)作为能量的函数在临界能量umic发生如图所示的弯折现象。
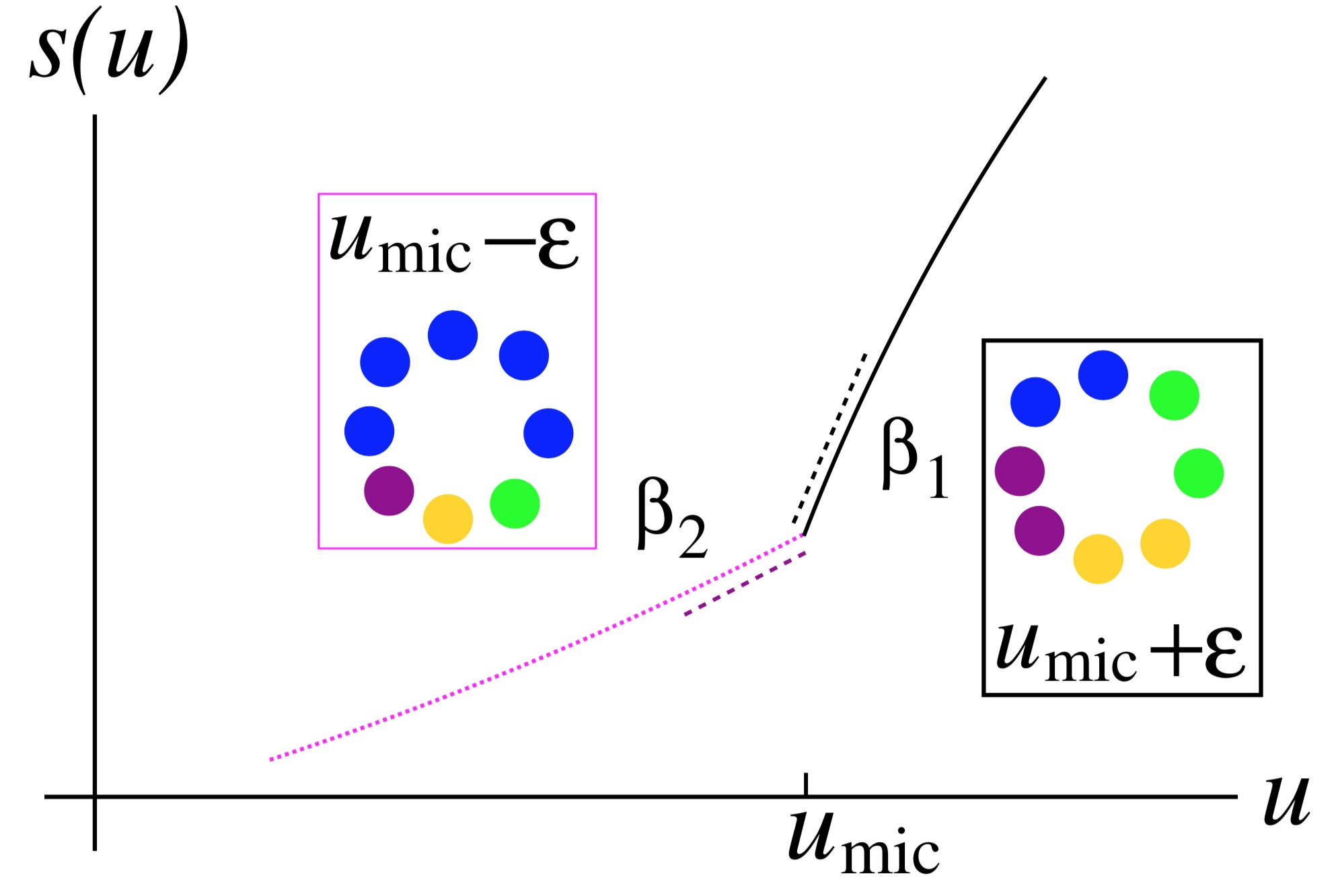 |
这项工作表明,统计物理系统的自发对称性破缺并不总是能量和熵的相互妥协过程。在固定能量下,纯粹的熵效应也可使系统从宏观无序状态自发地演化到宏观有序状态,而且在演化过程中该绝热系统的温度会自发地升高。
相传当年达摩禅师在嵩山面壁九年,处于准静态很少吃喝,内能应该在缓慢减少;突一日头上热气腾腾,脑中豁然开朗,因空见色,如幻如电。这会不会就是脑神经网络系统出现了自发对称性破缺的外在表征?也许达摩禅师当年实际上在从事统计物理研究哩。
周海军研究员的这项工作受到国家自然科学基金委(基金号11421063)和中国科学院(基金号QYZDJ-SSW-SYS018)的支持,其中涉及的计算机模拟工作是在中国科学院理论物理研究所的天问计算机集群和广州天河二号超级计算机集群上完成的,同时也感谢理论物理前沿重点实验室的支持。
文章链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.160601
