量子杂质问题中一个典型的模型是J.Kondo在解释磁性物质中剩余电阻时提出来的,后来被人们称为Kondo模型。人们发现可以通过重整化群的方法定性地理解Kondo模型的基态性质以及铁磁反铁磁相变。直到1975年Wilson发展了数值重整化群方法(NRG),Kondo模型的基态性质才得以通过数值方法定量化的研究。随着包括NRG和DMRG等数值技术的快速发展,人们已经可以精确处理各种一维杂质系统中的平衡态问题。
近年来,随着量子模拟技术的发展,人们可以在光晶格中的冷原子系统中实现量子杂质模型,例如Kondo模型,并从实验上研究整个系统(包括杂质及费米海)的远离平衡态的动力学。这就要求在理论上全面理解量子杂质系统的非平衡动力学行为。而目前已知的数值方法,例如,NRG和DMRG,局限于处理长时间演化的问题,并且会消耗大量的计算资源。因此,希望发展一套系统的理论方法来更为有效地研究杂质模型中平衡态和远离平衡态的物理性质。
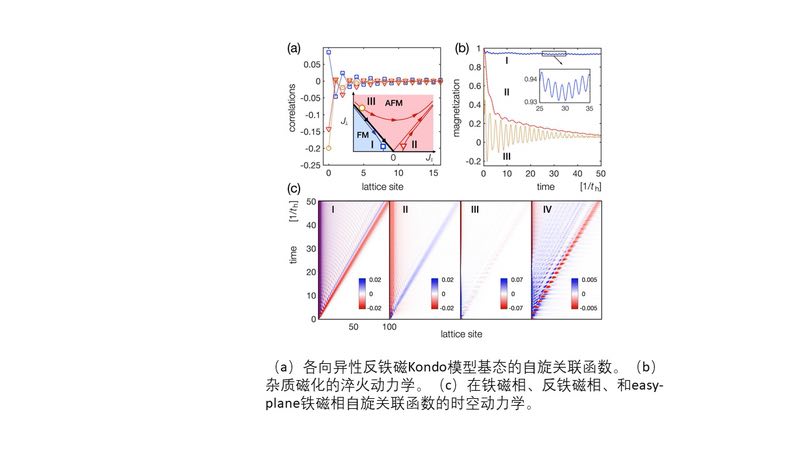
在此工作中,石弢及合作者利用体系的宇称发现了一种新的幺正变换,并将这种变换与高斯态理论结合,提出了描述量子杂质模型中平衡态及远离平衡态的变分波函数。这个变分态有效地刻画了杂质与热库中费米子的纠缠,并成功地给出了Kondo模型的微分电导,时空演化动力学性质,关联函数以及弛豫时间的普适行为等。这些结果与以往的解析和数值结果均符合。除此之外,还预言了在easy-plane Kondo模型中的一种新型的非平衡现象,也就是长时间的量子渐跃行为。可以推广这种方法来研究量子杂质模型(例如Anderson模型)中很多未解决的非平衡动力学问题。
该工作由中国科学院理论物理研究所石弢副研究员及其在马普量子光学研究所、哈佛大学、以及日本东京大学的合作者共同完成。此研究工作是量子光学,量子信息和凝聚态物理领域交叉合作的研究成果。