在标准量子统计物理中，费米-狄拉克、玻色-爱因斯坦等各种热平衡分布的实现离不开一个基本要素：系综。但是，众所周知，系综概念具虚拟本质。能否不引入系综，对按确定动力学规律演化、真实的“单个”系统直接建立统计物理描述？冯·诺伊曼、朗道等杰出物理学家很早就认识到这个问题在统计物理基础中的核心地位。但是直到1994年，M. Srednicki才借助于量子混沌的基本猜想—贝里猜想，即量子混沌系统的本征波函数在大空间尺度呈现均匀结构—证明：刚球系统的单个本征波函数就好比一个热库，足以产生热平衡分布。这个结果为量子统计物理基础带来了全新的观点，并在近年推动了大量的理论和实验研究。 然而，证明贝里猜想本身是一个极端困难的任务；事实上，人们迄今未能证明该猜想。贝里猜想对于量子统计物理基础是本质的吗？在什么条件下平衡统计物理可在单个本征态的水平实现？微观粒子间的碰撞即“直接”相互作用是不是如一般认为的那样，是不可缺少的成分？这些是迫切需要回答的更为重要的核心问题。
　　围绕这些问题，近年来，中科院理论物理研究所田矗舜研究员和合作者对量子多体系统的一个基本特性，即全同粒子不可区分性，或微观粒子间的交换相互作用在本征态统计物理基础中的作用进行了深入研究，并在近期取得重要进展。相关论文作为Rapid Communication发表于著名统计物理杂志Physical Review E。在这个工作中，作者解析地证明，作为描述量子多体系统微观状态基本骨架的福克空间隐藏着一个热结构。这里“隐藏”包括两方面含义，第一，对于绝大部分福克态，虽然相应的粒子数占据构型看起来很不规则，但在好量子数空间却呈现大尺度规则结构，该结构由费米-狄拉克分布或玻色-爱因斯坦分布描述（参见附图）；并且，这个结构的出现与量子系统的动力学性质，如可积、混沌、安德森局域化等等无关。第二，只有选取合适的物理量，我们才能“探测”到该热结构，即该物理量在给定福克态下的量子期望值等于热平衡分布的平均值；但是，物理量的选取与系统的量子动力学性质密切相关：如对于可积或安德森局域化系统，短程关联函数是合适的物理量，但长程不是，而对于量子混沌系统，短程和长程关联函数都是合适的物理量。
　　这个工作与近年来关于本征态统计物理的正统观点有诸多不同。首先，它表明了即使微观粒子间没有直接相互作用，交换相互作用就足以通过产生量子纠缠使平衡统计物理在单一本征态中呈展；其次，它表明了对于粒子间有直接相互作用的量子系统，贝里猜想并不是实现本征态平衡统计物理所必需的。这也就为研究无序关联电子系统的福克空间局域化及输运这个极富挑战性的前沿凝聚态物理问题开辟了新途径。
　　有趣的是，这个工作还首次阐明了本征态统计物理和随机几何体的极限形之间的深刻联系。后者由前苏联数学家A. Vershik于上世纪70年代在研究表示论时发现，并被其学派应用于大整数的随机分拆这个数论基本问题的研究。Vershik学派所取得的一些深刻结果是本工作中某些一般结果的特例。极限形理论和Seiberg-Witten理论的联系已被A. Okunkov等数学家发现。
　　此工作得到了国家自然科学基金委重点项目“小量子系统的动力学研究”、中科院理论物理前沿重点实验室和国家自然科学基金委理论物理专款“彭桓武理论物理创新研究中心”的支持。
　　论文链接：https://journals.aps.org/pre/abstract/10.1103/PhysRevE.98.060103
　　
　　
　　
　　
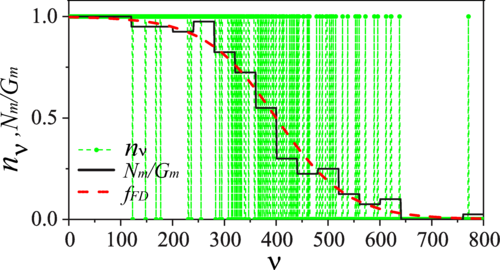
　　附图：隐藏在费米子系统福克空间中的热结构